Volume 21, No.2 Pages 91 - 95

1. Introduction
　Magnetic Compton scattering is an established experimental technique, used extensively on beamline BL08W at SPring-8. The objective of this long term project was to install and commission a new sample environment, and then to perform experiments using it. Previously, the sample environment was capable of obtaining temperatures down to 6 K and magnetic fields up to 2.5 T. The new Oxford Instruments "Spectromag" cryomagnet, which is the property of the University of Warwick, extended these parameters to provide a minimum temperature of 1.5 K and a maximum field of 9 T, as depicted in figure 1.

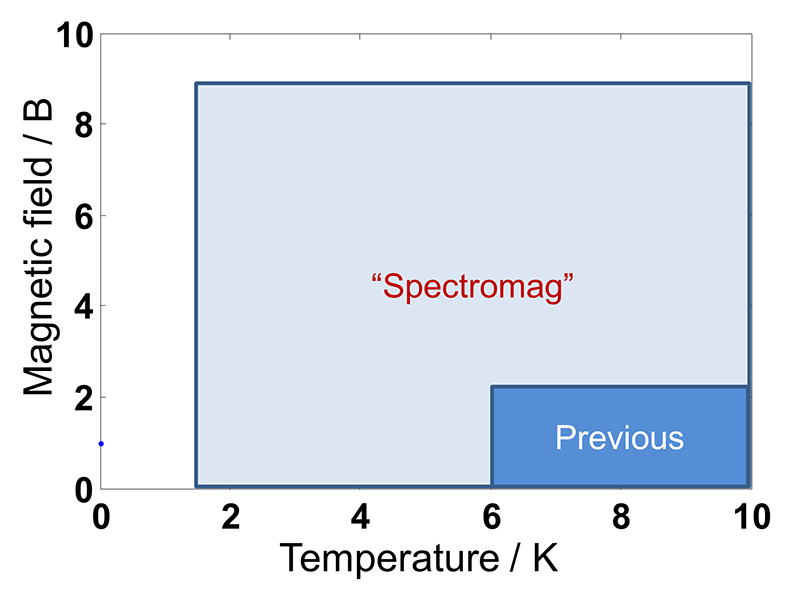
Figure 1   A graphical respresentation of the temperatures and magnetic fields achievable with the new sample environment.

　The magnetic Compton scattering experimental technique enables the study of the spin resolved electron momentum density of a magnetic material via measurements of the inelastic scattering of high energy circularly polarised X-rays. The interpretation of the results typcially requires electronic structure calculations, and hence, the technique provides insight into the underlying electronic structure of the material studied. The method is suitable for materials with a net magnetic moment: ferromagnets and ferrimagnets, and also other systems where the applied magnetic field induces a moment.
　The experiments utilise non-resonant inelastic, or "Compton", scattering of monochromatic high energy (typically 175 keV) photons from the sample. Figure 2 depicts the experimental geometry. The high scattering angle, of 175° is used to optimise the magnetic signal and the experimental resolution. When the X-rays are inelastically scattered by the electrons in the sample, the photon energy distribution measured at a set scattering angle is Doppler broadened because of the electrons' momentum distribution. A measurement of the photon energy spectrum can be directly related to a 1-dimensional projection of the electron momentum distribution of the sample. In order to make the spin-resolved measurements, circularly polarised photons are required, and a reversible magnetic field is applied to the sample. This permits a spin-dependent term in the scattering cross-section to be exploited. A measurement involves reversing the applied field and taking the difference between the two spectra collected. The charge scattering cancels out, leaving the spin contribution. Hence the resultant measurement, or magnetic Compton profile (MCP), represents the electron momentum density of only those electrons that contribute to the spin magnetic moment of the sample.

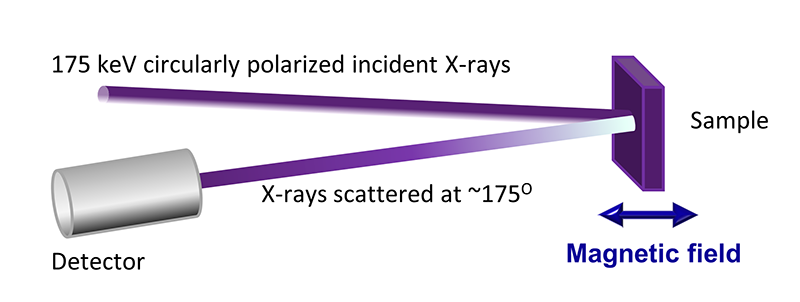
Figure 2   A schematic representation of the geometry adopted for magnetic Compton scattering experiments.

　Once the scattering cross-section and normalisation have been applied, the MCP, J_mag, is defined as the 1D projection of the spin-polarized electron momentum density:

J_mag = ∫∫ (ρ_↑ − ρ_↓) dp_x dp_y

　Here ρ_↑ and ρ_↓ are taken as the electron momentum densities of the majority and minority spin bands. Since the MCP is the difference between two measured Compton profiles, components arising from spin-paired electrons cancel, as do most sources of systematic error. Because only those electrons that contribute to the spin moment of the sample contribute to the MCP, the sample's spin magnetic moment can be determined. Such measurements can provide valuable information in systems where the spin and orbital moments contributions to a known bulk magnetic moment are unknown or not fully understood, as discussed in our previous work on the temperature dependence of the spin and orbital moments in magnetite^[1][1] J. A. Duffy et al.: Phys. Rev. B 81 (2010) 134424..
　The magnetic Compton profile is particularly useful because electrons originating from different orbitals have different momentum density distributions. For example, well localised electrons, such as those in the 4f orbital (for example in Gd) have a broad contribution to the MCP whereas more itinerant electrons (for example the 5d electrons in Gd) have a narrow momentum density distribution. In order to interpret measured MCPs, electronic structure calculations are used, from which the resultant theoretical spin-dependent momentum distributions and hence the MCPs can be calculated. The electronic structure calculations can be used as the basis for fitting to the data to reveal the physics, rather than relying on purely ab-initio calculations. For example, in previous work that we have performed on BL08W, we showed that Fe-rich NbFe₂ has ferrimagnetic order by using calculations for different possible magnetic ground states^[2][2] T. D. Haynes et al.: Phys. Rev. B 85 (2012) 115137., and were able to determine the Fermi level spin polarisation in the Co_(1-X)Fe_XS₂ system^[3][3] C. Utfeld et al.: Phys. Rev. Lett. 103 (2009) 226403.. As part of this project, we have developed software^[4][4] D. Ernsting et al.: J. Phys.: Condens. Matter 26 (2014) 495501. to calculate MCPs from theoretical electronic structure outputs that are output by the ELK package^[5][5] http://elk.sourceforge.net.
　There are several important reasons for developing the high field method. Measurements of a considerably wider range of materials, including those which have interesting high-field behaviour, such as metamagnetism, will become possible. Furthermore, in many small-moment systems the high field will induce a larger moment, making measurements more sensitive and hence faster. The effective count rate is proportional to the square of the induced moment, and hence, for example a five-fold increase in the moment makes a measurement twenty five times faster, such that we can study systems which would previously have required too much beamtime.

2. Experimental Details
2.1 The experimental set up
　The main goal of the project was to implement high-field, low-temperature, magnetic Compton scattering experiments on beamline BL08W, by installing and commissioning our "Spectromag" cryomagnet. The development of the experimental technique made possible by this long term project, together with advances in the theoretical modelling and interpretation, mean that we have a methodology ready for exploitation for new measurements by ourselves and other users of BL08W.
　As discussed above, monochromatic X-rays of energy 175 keV were used for these experiments. The beamline's helical wiggler was used to obtain the required circular polarisation. The scattering geometry adopted was based on that depicted in figure 2. The cryomagnet is shown as set up for an experiment in figure 3a. The incident X-ray beam passes through the beampipe to the sample, which is held within the cryostat. The Ge detector, positioned towards the front in the photograph, consists of ten elements arranged in a circle, such that the incident beam passes through the circle centre. All ten elements then have the same scattering angle.

Figure 3   (a) The cryomagnet in-situ on BL08W. The incident X-ray beam enters via the evacuate beampipe at the bottom of the photograph. The Compton-scattered X-rays travel back along the beampipe to the multi-element detector. (b) The sample holder, consisting of the miniature goniometer and cradle.

　Figure 3b shows a sample attached to a non-magnetic miniature goniometer in our custom-built holder. This permits accurate sample alignment with respect to the X-ray beam. Crystallographic alignment is not possible in-situ, and is instead performed prior to the experiment, normally using an X-ray Laue instrument. Our sample holder enables this alignment to be preserved when the sample is transferred to the magnet for the experiment.
　The associated magnet power supply and electronics are not shown in the figure, but these are interfaced with the beamline experimental control computer.

2.2 Experimental Procedure
　The new experimental system required the development and testing of a new experimental procedure. This was because, whilst the magnet coil configuration permits high magnetic fields, the field ramps more slowly than the original cryomagnet. As discussed above, obtaining an MCP requires a difference measurement to be made. To do this, the magnetic field is reversed and data collected for fields parallel and anti-parallel to the X-ray scattering vector. The magnetic signal is often less than 0.5% of the charge scattering, and hence very good normalisation is crucial. The procedure adopted is shown in figure 4a, showing the typical "ABBA" method, where A and B represent the two magnetic field directions. For the original magnet, the measurements consisted of 1-minute counts, with the field reversal taking a few seconds. Because of the slower ramp rate of the new magnet, it was important to utilise much longer counting times. The counting times can be chosen to be the most appropriate for a particular experiment: in figure 4a we just depict 5 minutes and 30 minutes versions, with a comparison of the results obtained shown in figure 4b. For this measurement, a single crystal Ni sample was used. This test measurement was used to show that very good normalisation is feasible even for long counting times.

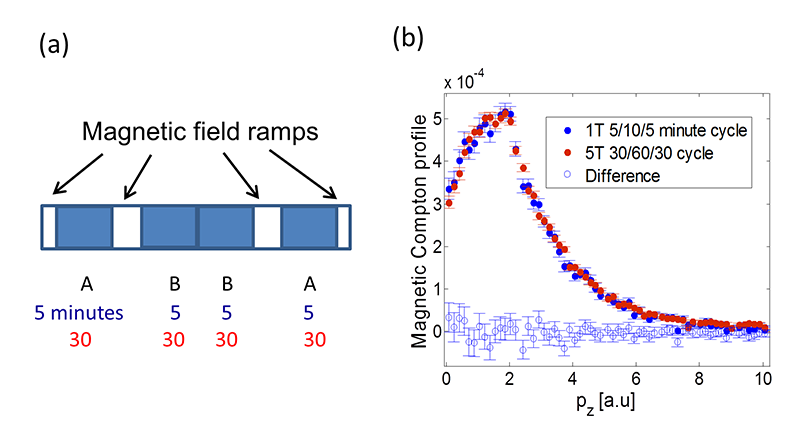
Figure 4   (a) A schematic representation of the procedure adopted to make a measurement. The labels A and B refer to the magnetic field being parallel and anti-parallel to the scattering vector. (b) Magnetic Compton profiles for ferromagnetic nickel, measured at 1 T and 5 T, using the counting times shown in (a).

3. Results
　During the course of the long term project, we have made several measurements. In this section, we present two particular examples in order to demonstrate the experimental technique: a full interpretation of the results will be published in detail elsewhere.

3.1 Frustrated Ca₃Co₂O₆
　Ca₃Co₂O₆ is a rather intriguing material. It has an unusual electronic ground state, in which the Co 3d orbital occupation does not lead to the usual crystal field quenching of the orbital magnetic moment. It is also a frustrated system, and exhibits a number of metamagnetic transitions with a complicated temperature dependence. Our work here is aimed at gaining a better understanding of the electronic configuration that underlies the magnetic properties. In our experiment, we determine the spin moment to be 3.93 ± 0.05 μ_B at 10 K, with an applied field of 7 T. By comparison with the bulk magnetic moment of 5.2 ± 0.1 μ_B, the orbital moment is 1.3 ± 0.1 μ_B. Such an orbital moment is unusual in 3d transition metal systems, but it is consistent with expected ground state here, where the orbital moment is predicted to be unquenched^[6][6] H. Wu et al.: Phys. Rev. Lett. 95 (2005) 186401.. In figure 5, we show the measured MCP along with our molecular orbital calculation using orbitals based on the previous theoretical results^[6][6] H. Wu et al.: Phys. Rev. Lett. 95 (2005) 186401., which, as well as predicting the orbital moment, suggested that there would be a significant oxygen 2p polarisation. It has been suggested that the trigonal Co³⁺ site was described better as Co²⁺Oh (i.e. an electron is donated to the Co by the oxygen). However, our data strongly suggest that this model is incorrect. Firstly, there is a discrepancy at low momentum, although it should be noted that this is often apparent in magnetic Compton profiles. Secondly, and significantly, the orbital occupations, as shown below, are not physically feasible: in particular the hybridised xz / yz orbitals would have a spin moment greater than 2 μ_B and the x²-y² / xy hybridised orbitals are not expected to have a negative moment.

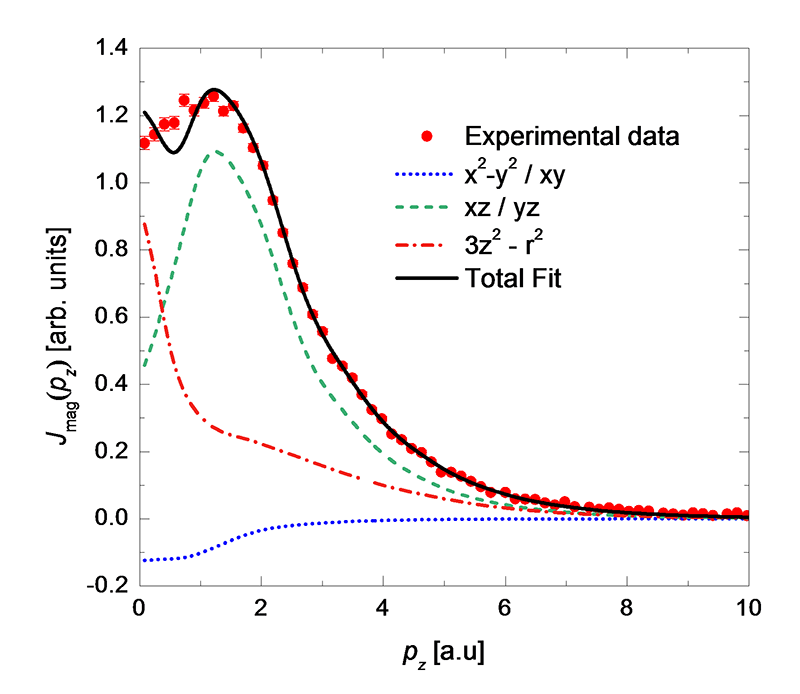
Figure 5   The MCP together with the results of a CoO₆^6- cluster calculation for Co-O orbitals. Whilst it looks like a good fit, it is unphysical (the fitted value of the spin moment in the xz / yz degenerate orbitals is impossible). Our data are not consistent with previously published theoretical predictions for the material's magnetic ground-state.

3.2 CeB₆: evidence for anisotropy
　In an applied magnetic field, CeB₆ has a ferromagnetic moment that is believed to exist on its 4f electron: the moment is a combination of an orbital moment, with a smaller negatively polarised spin moment, as would be expected from Hund's rules. Some previous work using polarised neutron diffraction was consistent with this, showing an isotropic magnetisation density which could be modelled using local 4f orbitals^[7][7] F. Givord et al.: J. Phys.: Condens. Matter 15 (2003) 3095.. However, other work together with muon spectroscopy results^[8][8] A. Schenck et al.: Phys. Rev. Lett. 89 (2002) 037201. were interpreted as showing an "anomalous" itinerant spin density. Our work was motivated by the unresolved controversy concerning the magnetisation density, and the new interest in CeB₆ (for example see reference^[9][9] H. Jang et al.: Nature Mat. 13 (2014) 682-687.).
　Magnetic Compton scattering is a particularly useful technique to study this material, because it is only sensitive to the spin moment, and crucially because it is sensitive to all electrons that contribute to the magnetism. The polarised neutron diffraction technique is sensitive to the total magnetic moment: in CeB₆, the spin and orbital moments are antiparallel, resulting a small total magnetic moment. Furthermore, the method would not be sensitive to an itinerant contribution to the magnetic moment as found in the NMR work.
　Figure 6 depicts our experimental data resolved along the [100] and [110] crystallographic directions, together with isotropic relativistic Hartree Fock calculations for Ce 4f and 5d orbitals. The spin moment is -0.286 ± 0.007 μ_B, at T = 1.5 K, B = 6 T, with the total and orbital moments being 0.844 ± 0.009 μ_B and 1.128 ± 0.000 μ_B, respectively. The first clear observation is that the spin density is anisotropic. This was unexpected from the polarised neutron diffraction data, and hence we performed tests to ensure that our result is robust. In order to account for the measurements, a model is required that is consistent with both of the directional profiles: it can be seen that a 5d orbital appears to be consistent with the [100] data, but not the [110], and hence does not provide a description of the true ground state. An interpretation of the magnetism as revealed by our measurements will be published elsewhere, but we note here the clear importance of studying single crystals whenever possible, rather than polycrystalline samples.

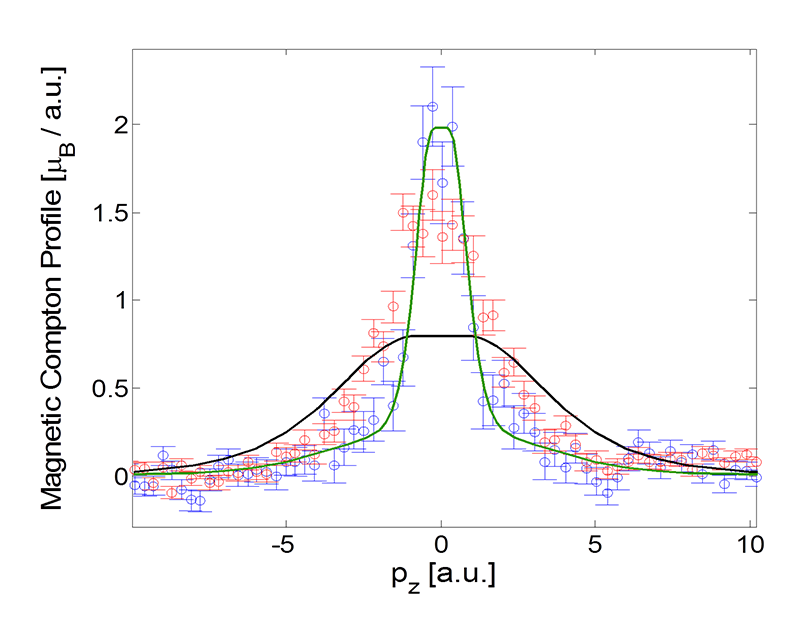
Figure 6   Spin density in CeB₆ at B = 6 T, T = 1.5 K, resolved along two crystallographic axes: blue data [100] and red data [110]. The black and green lines depict isotropic 4f and 5d orbital electrons respectively. Note that the spin moment is negative, i.e. it is antiparallel to the net moment (and the orbital moment).

4. Conclusions
　Magnetic Compton scattering experiments can now be performed on the BL08W beamline in a sample environment that can provide magnetic fields up to 9 T and temperatures down to 1.5 K. The established experimental technique can now be applied to materials that could not previously be studied.

Acknowledgments
　We gratefully acknowledge the provision of beam time at SPring-8 by JASRI (Proposal number 2012B0045-2015A0045: Long-term Proposal). We would also like to thank M. Itou, Y. Sakurai and the staff for their support and assistance. We acknowledge the financial support of the EPSRC (UK) via research grants EP/F021518 and EP/J003492.

References
[1] J. A. Duffy et al.: Phys. Rev. B 81 (2010) 134424.
[2] T. D. Haynes et al.: Phys. Rev. B 85 (2012) 115137.
[3] C. Utfeld et al.: Phys. Rev. Lett. 103 (2009) 226403.
[4] D. Ernsting et al.: J. Phys.: Condens. Matter 26 (2014) 495501.
[5] http://elk.sourceforge.net
[6] H. Wu et al.: Phys. Rev. Lett. 95 (2005) 186401.
[7] F. Givord et al.: J. Phys.: Condens. Matter 15 (2003) 3095.
[8] A. Schenck et al.: Phys. Rev. Lett. 89 (2002) 037201.
[9] H. Jang et al.: Nature Mat. 13 (2014) 682-687.