Volume 30, No.1 Pages 2 - 6

1. はじめに
　近年、従来のシリコン半導体の性能を凌駕する化合物半導体として、窒化物半導体の研究開発が精力的に行われている。特に窒化ガリウム（GaN）は大きな絶縁破壊電界や飽和電子速度を有し、大電力・高速動作に適した特性を有するため、次世代パワーデバイスとして電動車や高速通信への応用が期待されている。しかしながら、現在用いられているGaN結晶ウェハーには密度にして10³-10⁶ cm^-2程度の貫通転位（原子位置がずれた領域がウェハーを貫く方向に線状に続いた欠陥）が含まれており、デバイスの電気特性や信頼性に大きな影響を与えている。転位に由来する拡張欠陥や転位の反応が結晶の残留歪みや塑性特性に影響して、反りやクラックといったウェハースケールの問題を引き起こしたり、転位の歪場との相互作用により不純物が偏析しデバイスの電気的特性に影響を及ぼすと考えられている。転位には転位線（転位の伝搬方向）とバーガースベクトルb（原子のずれ・変位を表すベクトル）の関係によりらせん転位（転位線とbが平行）、刃状転位（転位線とbが垂直）、混合転位（らせんと刃状両方の成分をもつ）の3種類があり、転位種により歪分布と電気特性への影響が異なることが知られている。したがって、転位とそれに伴う歪場の性質を十分に理解し制御することが、デバイスの開発や高性能化にとって必要不可欠である。これらの転位に伴う歪みを観察するために従来用いられてきた手法として、透過型電子顕微鏡（TEM）ベースの幾何位相解析（GPA）^[1][1] M. J. Hÿtch, J-L. Putaux and J-M. Pénisson: Nature 270 (2003) 423.やラマン分光法^[2][2] N. Kokubo, Y. Tsunooka, F. Fujie, J. Ohara, S. Onda, H. Yamada, M. Shimizu, S. Harada, M. Tagawa and T. Ujihara: Jpn. J. Appl. Phys. 58 (2019) SCCB06.、X線トポグラフィ法^[3][3] T. Ohno, H. Yamaguchi, S. Kuroda, K. Kojima, T. Suzuki and K. Arai: J. Cryst. Growth 209 (2004) 260.があげられる。TEM-GPAでは転位コア周辺ナノメートル領域の観察が可能であるが、サンプルの薄片化が必要な破壊分析であり、また転位線とバーガースベクトルが平行になるらせん転位の観察は困難である。一方、ラマン分光法とX線トポグラフィ法は非破壊分析であるが、前者はTEM-GPAと同様、らせん転位の判別が困難であり、後者は歪みの定量分析が困難であるという問題がある。このように、転位の歪場を非破壊で定量的に解析する手法は完全には確立されていないのが現状である。
　われわれのグループはこれまでに、放射光で得られるナノメートルサイズのX線ビームを用いたナノビームX線回折（nanoXRD）により、半導体結晶の局所における結晶微細構造を定量的に解析する手法を開発してきた^{[4, 5]}[4] S. Kamada, S. Takeuchi, D. T. Khan, H. Miyake, K. Hiramatsu, Y. Imai, S. Kimura and A. Sakai: Appl. Phys. Express 9 (2016) 111001.
[5] K. Shida, N. Yamamoto, T. Tohei, M. Imanishi, Y. Mori, K. Sumitani, Y. Imai, S. Kimura and A. Sakai: Jpn. J. Appl. Phys. 58 (2019) SCCB16.。nanoXRDにもとづく3次元逆格子空間（ω-2θ-φ）マップで測定される格子面微細構造（格子面の間隔、傾斜、および回転）の変化から、歪テンソルの各成分を直接評価することができる。高い歪分解能と空間分解能を有するnanoXRD法を用いて3次元逆格子空間マッピングの位置依存測定を行うことで、原理的には転位周辺に広がる3次元的な歪場の全ての成分を検出し、転位種の判別と歪場強度の定量化が可能であると期待される。本稿では、nanoXRD法による歪の定量分析の新たな試みとして、Naフラックス法により作製したバルクGaN結晶中の単独転位周辺の歪テンソルの解析を行った研究について紹介する^[6][6] T. Hamachi, T. Tohei, Y. Hayashi, S. Usami, M. Imanishi, Y. Mori, K. Sumitani, Y. Imai, S. Kimura and A. Sakai: J. Appl. Phys. 135 (2024) 225702.。

2. ナノビームX線回折逆格子空間マッピング測定
　本実験では、エッチピット法により予め転位の位置と種類を特定したGaN基板について、個別の転位に照準したnanoXRD逆格子マッピング測定を行い、転位周辺の歪場の定量解析を行った。分析対象の試料として、Naフラックス法により作製したGaNバルク基板上にHVPE法でホモエピタキシャル成長させたGaN結晶^[7][7] Y. Mori, M. Imanishi, K. Murakami and M. Yoshimura: Jpn. J. Appl. Phys. 58 (2019) SC0803.を用いた。まず、化学機械研磨（CMP）法により研磨したGaN（0001）結晶表面に、化学薬液（KOH + NaOH）によるエッチング処理を行った。転位がある箇所では結晶の歪みによりエッチングが局所的に促進され、エッチピットと呼ばれるくぼみができる。先行研究から、転位のバーガースベクトルの違いにより異なるサイズのエッチピットが形成されることがわかっており^[8][8] T. Hamachi, T. Tohei, Y. Hayashi, M. Imanishi, S. Usami, Y. Mori and A. Sakai: J. Appl. Phys. 129 (2021) 225701.、本試料ではb = <1-101> = 1m + 1cの混合転位に対応するLサイズエッチピット、およびb = 1/3<11-20> = 1aの刃状転位に対応するXSサイズエッチピットの形成を確認した。その後表面を再度CMP研磨し、多光子励起顕微鏡（MPPL）により転位の分布と伝搬挙動を観察した。MPPL観察において転位は暗点として観察され、各サイズのエッチピットに対応する転位の位置を特定することができる。
　このようにして転位の位置を把握したGaN結晶表面に対して、nanoXRD法による歪解析を行った。nanoXRD測定実験はSPring-8 BL13XUのX線回折光学系を用いて行った。8 keVのエネルギーをもつX線（波長0.15498 nm）を二結晶Si（111）モノクロメータにより単色化し、ゾーンプレートを用いて集光することでビームサイズ480 nm × 770 nmのX線ナノビームを形成した。回折実験のジオメトリを図1に示す。X線はGaN結晶の［11-20］に平行に入射し、（0004）対称面および（11-24）非対称面の反射を用いて逆格子マップの測定を行った。回折X線強度の測定には2次元検出器（HyPix-3000, Rigaku）を用いた。入射角ωを走査しながら2次元検出器を用いて回折像（2θ–φマップ）を取得することで、ω–2θ–φ 3次元（3D）逆格子空間マッピング像を得ることができる^[4][4] S. Kamada, S. Takeuchi, D. T. Khan, H. Miyake, K. Hiramatsu, Y. Imai, S. Kimura and A. Sakai: Appl. Phys. Express 9 (2016) 111001.。本実験ではLサイズおよびXSサイズエッチピットの転位を含む試料表面上の約20 × 20 μm²の領域で、［11-20］方向および［-1100］方向にそれぞれ800 nmおよび500 nmステップ毎にX線プローブ位置を走査して3次元逆格子空間マップデータを取得した。エッチピット形成およびMPPL観察により把握した転位の分布マップにもとづき、集束イオンビーム法により位置基準のPtマーカーを作製することで、目的の転位に照準した局所nanoXRD測定を行っている。

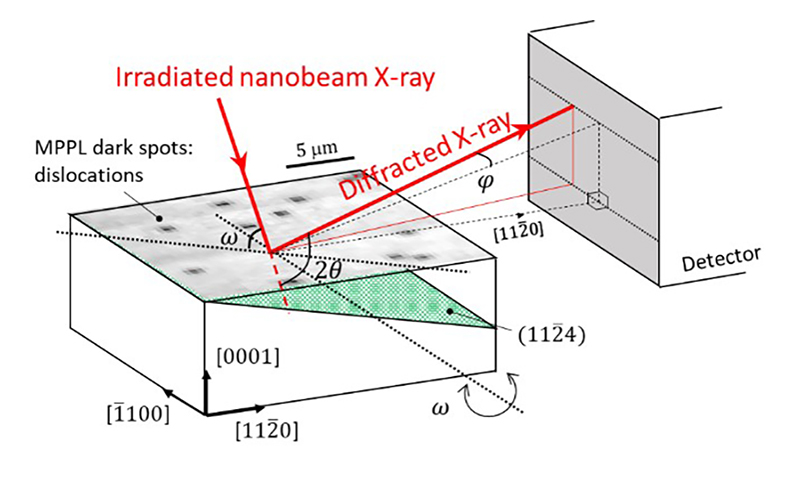
図1　nanoXRD ω-2θ-φ位置依存マッピング測定ジオメトリの模式図。

　取得したω–2θ–φ 3次元逆格子空間マッピングデータから、次節に示す解析式にもとづいて3次元の歪テンソルの成分を評価することができる。3次元逆格子空間マップをナノビームX線プローブを用いて高空間分解能で2次元サンプリング（位置依存性）測定することにより、転位周辺の歪場の分布を定量的に解析することを試みた。

3. GaN結晶中単独転位周辺の歪場テンソル解析
　上述の方法により、GaNバルク結晶の（0001）面上に形成したLサイズエッチピットおよびXSサイズエッチピットに対応する転位を含む領域において、3次元逆格子（ω–2θ–φ）マップの位置依存性を測定した。図2に位置依存ω–2θ–φ測定より得られたω, 2θ, φピーク位置（図2中ではΩ, 2Θ, Φと表記）の2Dマッピング結果を示す。たとえば格子面間隔に対応する2θの定量では、測定された3次元回折プロファイル（ω–2θ–φマップ）をω方向とφ方向にわたって積算し、1次元の2θプロファイルを得ることで、各測定点における2θのピーク位置とゆらぎ（Δ2θ）が算出される。ここで、ω, 2θ, φの値はそれぞれ格子面の傾き、面間隔、（面内）回転に対応する。図2に示すΩ, 2Θ, Φの位置依存マッピングの結果より、転位周辺の歪場を反映して、格子面傾斜、面間隔および格子面回転に局所的な変化が起こっていることがわかる。特に、バーガースベクトルの大きなLサイズエッチピット（図2の赤丸）に対応する転位の周辺で大きな結晶面の変化が起こっている様子が観察される。さらに、バーガースベクトルの小さなXSサイズエッチピット転位（緑丸）の位置における歪みの変化も観察されており、本結晶に含まれるすべての種類の転位が検出できていることがわかる（一部の転位で歪み変化の位置がややずれているのは、結晶中で転位が斜めに伝搬している可能性が考えられる）。

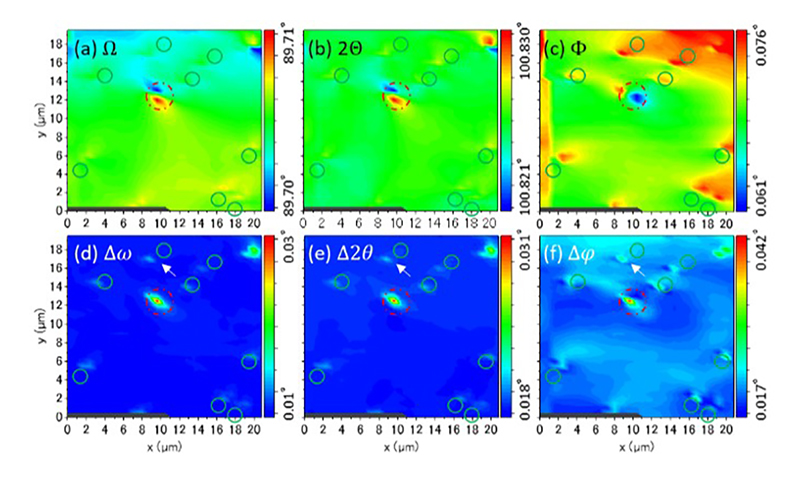
図2　位置依存ω-2θ-φマッピングデータから算出したΩ, 2Θ, Φ, Δω, Δ2θ, Δφの2Dマップ結果。

　これらのω, 2θ, φの値から、式（1）にもとづき、各測定点における逆格子点Q^pが求められる。

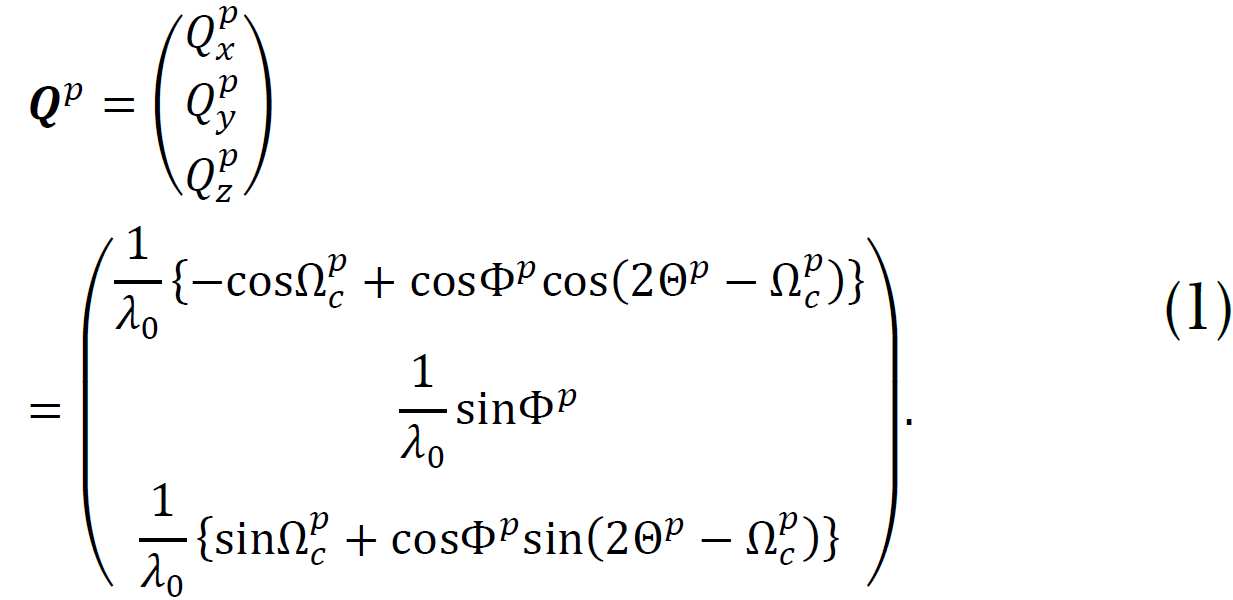
　ここでは対称面測定から求めた格子面傾斜の補正を反映したω, 2θ, φの値である。
　このように求められた逆格子点から、歪のテンソル成分が式（2）のように求められる。

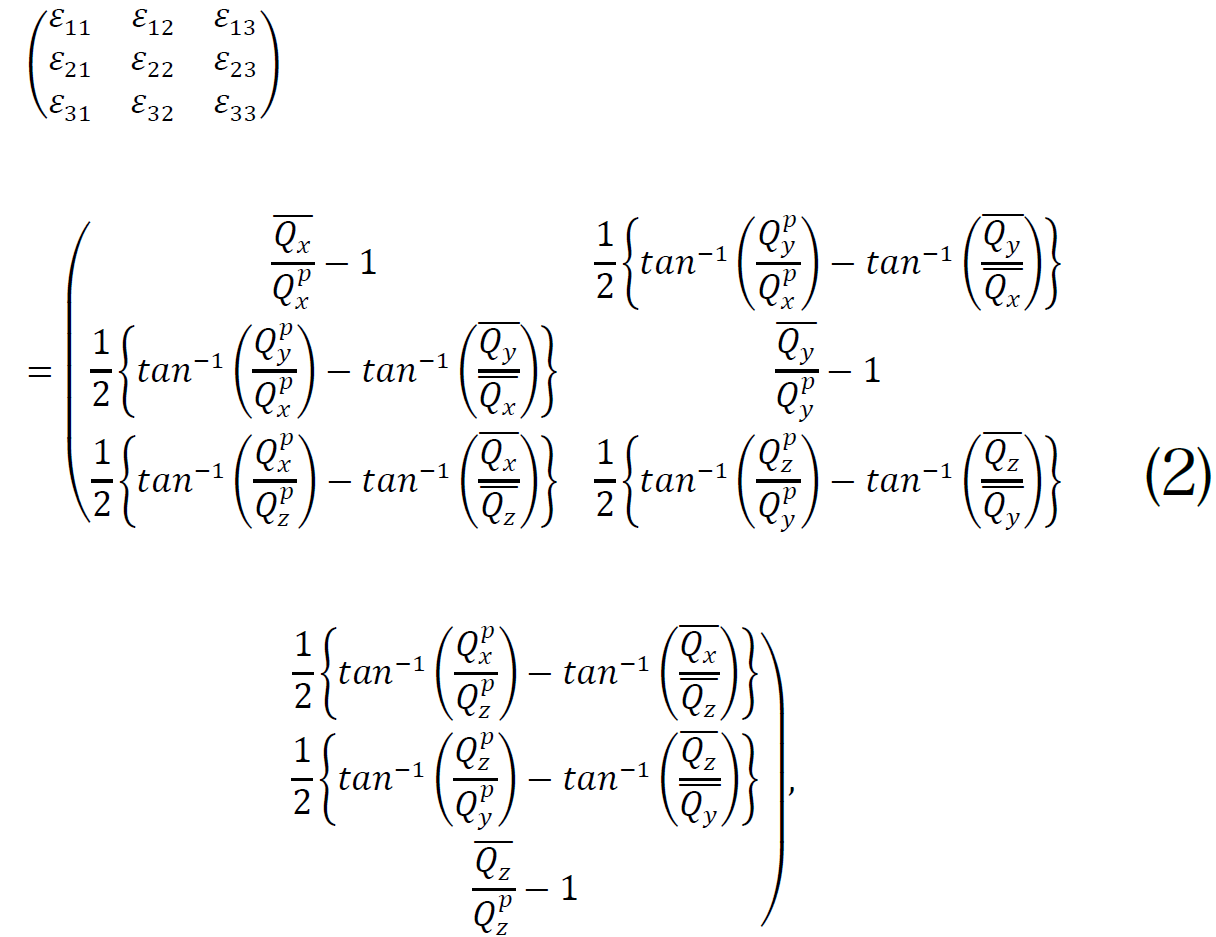
　ここで、は測定領域における逆格子点の平均値である。これらのε_ijとの関係を図示すると図3のようになる。たとえば、ε₁₁は面xに生じるx方向の歪、ε₁₂は面xに生じるy方向の歪（せん断歪）を表す。

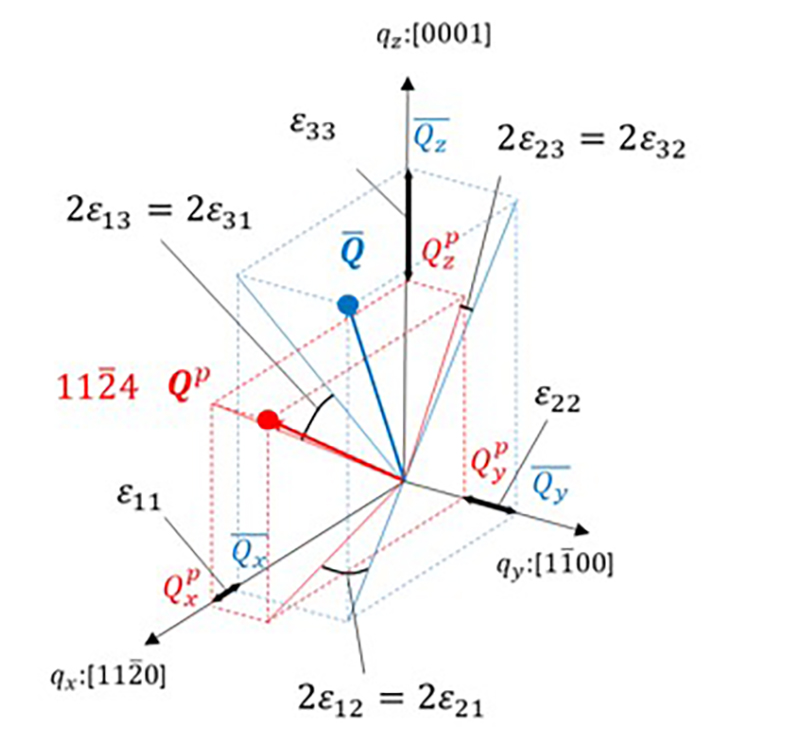
図3　逆格子点と歪み成分ε_ijの関係の模式図。

　一方、結晶中に原子位置が正規サイトからずれた原子変位欠陥（転位）が存在すると、その周辺に結晶が3次元的に歪んだ領域（歪場）が形成される。転位に関する弾性論のモデルから、刃状転位およびらせん転位が形成する歪場のテンソルは、それぞれ以下の式（3）、（4）のように表される^[9][9] M. Kato: Introduction to the theory of dislocations (seventh edition) (2020) Shokabo, Tokyo.。

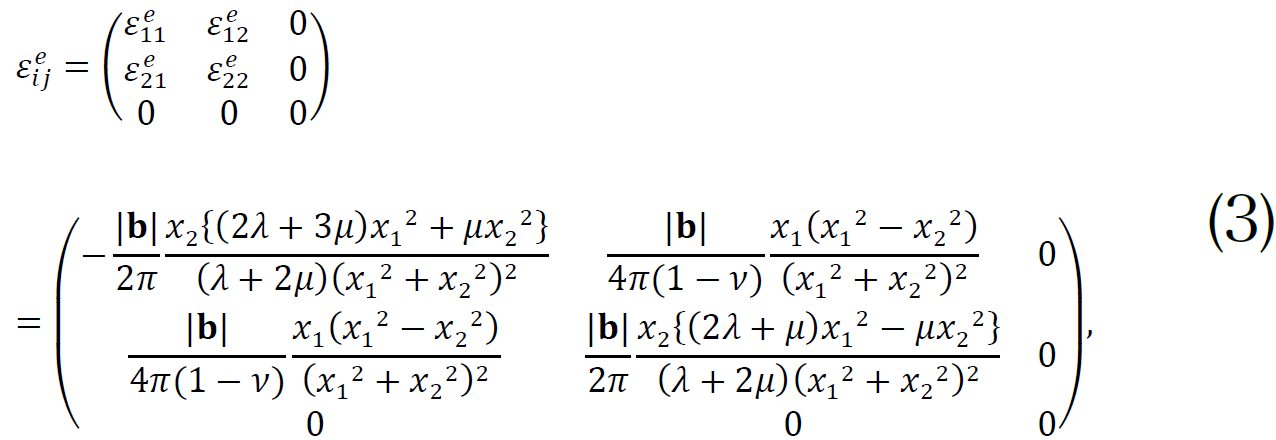
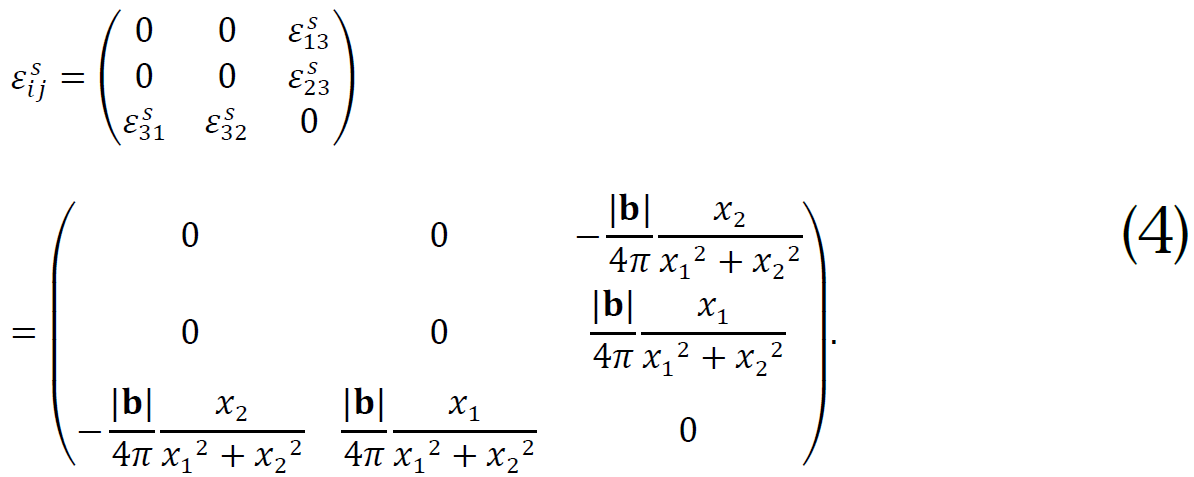
　ここで、bは転位の原子変位を表すバーガースベクトル、λ、μはラメ定数（弾性係数）、νはポアソン比である。これらの表式より、刃状転位はε₁₁とε₁₂歪成分を、らせん転位はε₁₃とε₂₃歪成分を持つことがわかる。また、混合転位では刃状成分に由来する歪とらせん成分に由来する歪の両方が生じると考えられる。本実験では、刃状、らせん、混合の各種の単独転位に照準してその周辺の歪場成分の測定を行った。
　図4に、本実験で観察した転位のうちLサイズエッチピットに対応した転位の周辺における歪場のテンソル成分の測定結果と、弾性論にもとづく計算値を比較して示す。このLサイズエッチピットの転位は先行研究からb = <1-101> = 1m + 1cの混合転位であることが示されており、刃状成分とらせん成分を有すると予想される。図4の歪マップ測定結果において、赤丸で示した転位位置の近傍で、刃状転位で存在するε₁₁, ε₁₂成分と、らせん転位で存在するε₁₃, ε₂₃成分の分布が実際に観察されていることがわかる。各歪成分のマッピング結果において、転位コアをはさんで正負の成分（双極子）が対称的に分布している。これは弾性論から予想される転位周辺の歪場の分布を良く再現している。弾性論から計算される歪場と測定結果の歪分布を比較することで、転位のバーガースベクトルの方向を非破壊で推定することができる（図4(e) - (h)の赤矢印）。特に、従来手法（GPAやラマン分光法）では観察が困難ならせん転位成分に関しても、その周辺の歪場を明瞭に検出し、バーガースベクトルの方向を推定することができている（図4(c), (d), (g), (h)）。

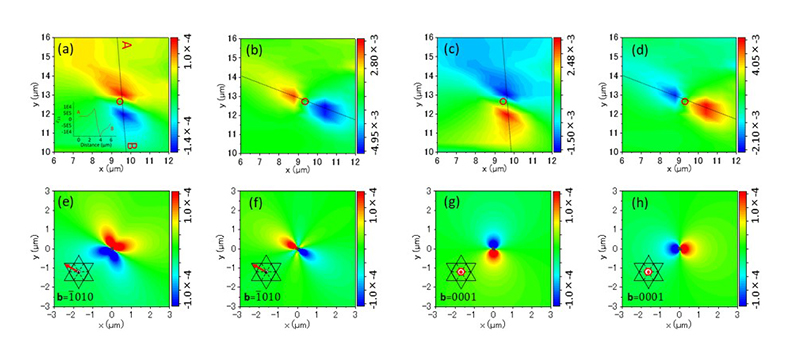
図4　Lサイズエッチピット転位（b = <1-101>）の歪成分(a)ε₁₁, (b)ε₁₂, (c)ε₁₃ (d)ε₂₃の測定結果と転位論から予測される歪みの計算値(e-h)の比較。計算値は刃状転位（b = <-1010>）のε₁₁,ε₁₂ (e, f)およびらせん転位（b = <0001>）のε₁₃,ε₂₃ (g, h)を示す。

　このように、本研究の方法により刃状転位に加えてらせん転位成分に由来する歪場も検出することができ、原理的には任意のバーガースベクトルを持つ転位の3次元歪テンソルの成分を解析することが可能である。GaNデバイスにおいて、らせん成分を持つ転位が電気特性（リーク電流）に顕著に影響することが指摘されており、本方法はらせん成分を有する転位を非破壊で検出するのに有効な手法になると期待される。また、転位歪場の強度（大きさ）に関して、測定歪の最大値から算出したb = 1m + 1cの混合転位とb = 1cのらせん転位のせん断歪成分ε₁₃およびε₂₃の大きさの比はほぼ1となっており、これはバーガースベクトルの値と弾性論から予想される結果とよく一致している。一方、b = 1m + 1cの混合転位とb = 1aの刃状転位の歪成分ε₁₁とε₁₂の比較においては、混合転位（b = 1m + 1c）のε₁₁, ε₁₂の大きさが、等方弾性体モデルからの予想値よりも大きくなっていることが観察された。ナノビームX線のプローブサイズによる空間分解能の制約から転位コア近傍の歪の最大値を厳密に評価することは難しいが、大きなバーガースベクトルを有する混合転位において不純物との相互作用や拡張欠陥の形成など特異的な転位反応が起こっている可能性が示唆される。
　従来手法との比較では、高分解能TEMをベースにしたGPA解析では、原子変位の実像観察にもとづきナノメートルオーダーの局所領域の分析が可能であるが、歪の分析感度は％のオーダーである。それに対してX線回折にもとづく本方法では、上述のように転位周辺マイクロメートル領域の歪場成分が観察されている。この歪場の形状はGPAにより観察されるnm領域の歪分布と基本的には相似的であるが、10^-4以下の歪感度にもとづきマイクロメートルオーダーに広がった歪場の検出が可能であり、結晶成長プロセスに起因する結晶微細構造の変化と合わせて、ウェハースケールでの解析やデバイス構造中での歪場の非破壊分析にも応用できると考えられる。

4. おわりに
　本稿では、ナノメートルサイズのX線ビームを用いて結晶中の歪成分を非破壊的に定量解析するナノビームX線回折法とGaN結晶転位の分析への応用について紹介した。ナノビームX線回折による高い空間分解能と歪み分解能によって、従来手法では特定が困難であった転位を歪成分の分布にもとづいて非破壊で検出・判別することができ、それにより、電気特性に異なる影響を与える転位を的確に把握し、結晶やデバイス開発に役立てることが可能になる。本方法は、GaN結晶だけでなく、パワーデバイス半導体としての研究開発が加速している炭化ケイ素（SiC）や酸化ガリウム結晶中の転位の分析にも応用でき、次世代半導体結晶・デバイスの開発と性能向上に貢献することが期待される。
　本稿で紹介した成果は、大阪大学の森勇介教授、林侑介助教（当時、現NIMS）をはじめとする皆さまとの共同研究によるものです。ここに深く感謝申し上げます。

参考文献
[1] M. J. Hÿtch, J-L. Putaux and J-M. Pénisson: Nature 270 (2003) 423.
[2] N. Kokubo, Y. Tsunooka, F. Fujie, J. Ohara, S. Onda, H. Yamada, M. Shimizu, S. Harada, M. Tagawa and T. Ujihara: Jpn. J. Appl. Phys. 58 (2019) SCCB06.
[3] T. Ohno, H. Yamaguchi, S. Kuroda, K. Kojima, T. Suzuki and K. Arai: J. Cryst. Growth 209 (2004) 260.
[4] S. Kamada, S. Takeuchi, D. T. Khan, H. Miyake, K. Hiramatsu, Y. Imai, S. Kimura and A. Sakai: Appl. Phys. Express 9 (2016) 111001.
[5] K. Shida, N. Yamamoto, T. Tohei, M. Imanishi, Y. Mori, K. Sumitani, Y. Imai, S. Kimura and A. Sakai: Jpn. J. Appl. Phys. 58 (2019) SCCB16.
[6] T. Hamachi, T. Tohei, Y. Hayashi, S. Usami, M. Imanishi, Y. Mori, K. Sumitani, Y. Imai, S. Kimura and A. Sakai: J. Appl. Phys. 135 (2024) 225702.
[7] Y. Mori, M. Imanishi, K. Murakami and M. Yoshimura: Jpn. J. Appl. Phys. 58 (2019) SC0803.
[8] T. Hamachi, T. Tohei, Y. Hayashi, M. Imanishi, S. Usami, Y. Mori and A. Sakai: J. Appl. Phys. 129 (2021) 225701.
[9] M. Kato: Introduction to the theory of dislocations (seventh edition) (2020) Shokabo, Tokyo.

藤平　哲也　TOHEI Tetsuya
大阪大学　大学院基礎工学研究科
システム創成専攻　電子光科学領域
〒560-8531　大阪府豊中市待兼山町1-3
TEL : 06-6850-6301
e-mail : tohei@ee.es.osaka-u.ac.jp

濱地　威明　HAMACHI Takeaki ^*
大阪大学　大学院基礎工学研究科
システム創成専攻　電子光科学領域
〒560-8531　大阪府豊中市待兼山町1-3
（^* 現 株式会社ミライズテクノロジーズ）

酒井　朗　SAKAI Akira
大阪大学　大学院基礎工学研究科
システム創成専攻　電子光科学領域
〒560-8531　大阪府豊中市待兼山町1-3

今井　康彦　IMAI Yasuhiko
（公財）高輝度光科学研究センター
放射光利用研究基盤センター
〒679-5198　兵庫県佐用町光都1-1-1

隅谷　和嗣　SUMITANI Kazushi
（公財）高輝度光科学研究センター
放射光利用研究基盤センター
〒679-5198　兵庫県佐用町光都1-1-1

木村　滋　KIMURA Shigeru
（公財）高輝度光科学研究センター
放射光利用研究基盤センター
〒679-5198　兵庫県佐用町光都1-1-1