Volume 29, No.3 Pages 185 - 189

1. はじめに：赤外放射光の利用研究
　赤外分光は、分子振動の研究などに用いられることが多い非常に汎用的な分光分析手法であり、ある程度の大きさをもつ試料の単純な透過・吸収測定であれば、市販の赤外分光装置（フーリエ変換赤外分光計、略称FTIR）を用いることで、短時間で簡便に行うことができる。しかし、市販装置に内蔵されている赤外光源は、高熱の物体が電磁波を放射する黒体輻射を利用した熱光源であり、輝度は低い。一方、赤外放射光の輝度は熱光源よりも2～3桁高いため、試料上の微小領域に光強度を集中させたい測定（顕微測定やマッピング測定など）や、空間的に制限された試料空間（高圧発生セルや超伝導磁石）における測定では、赤外放射光を用いた測定が有利になる^[1][1] S. Kimura and H. Okamura: J. Phys. Soc. Jpn. 82 (2013) 021004.。SPring-8の赤外ビームラインBL43IRでも、赤外放射光の高輝度性を活かした様々な実験が行われてきた^[2][2] 岡村英一他: 日本赤外線学会誌28 (2018) 48.。以下では、高圧下の赤外分光研究の例として、励起子絶縁体候補物質であるTa₂NiSe₅に対する筆者らの最近の研究^[3][3] H. Okamura et al.: Phys. Rev. B 107 (2023) 045141.を紹介する。

2. 励起子絶縁体とその候補物質Ta₂NiSe₅
　励起子絶縁体（Excitonic insulator、EI）とは、電子（e）と正孔（h）がクーロン引力により多数のe-h対（励起子）を自発的に形成し、集団凝縮することによってフェルミ準位（E_F）にギャップを生じるエキゾチックな絶縁体状態である^[4][4] 太田幸則他: 固体物理52 (2017) 119.。その存在は、まず1960年代に理論的に予測されたが、超伝導体においてe-e対（クーパー対）が集団凝縮して超伝導ギャップを生じることとの類似性もあり、大きな関心を集めた。図1に、理論的に予測されたEIの相図の概要を示す。EIの母体となる物質は半金属あるいは微小なギャップをもつ半導体であり、e-h相関が無いときの1粒子エネルギーギャップをE_gと定義している。ここでE_g > 0の場合（相図の右側）は半導体であり、E_g < 0の場合（相図の左側）はバンド重なりを持つ半金属である。E_g = 0近傍の転移温度T_c以下でEIが形成され、図1の上部に示すように、バンド端の分散が平坦化することがEIの特徴的振る舞いであるとされた。

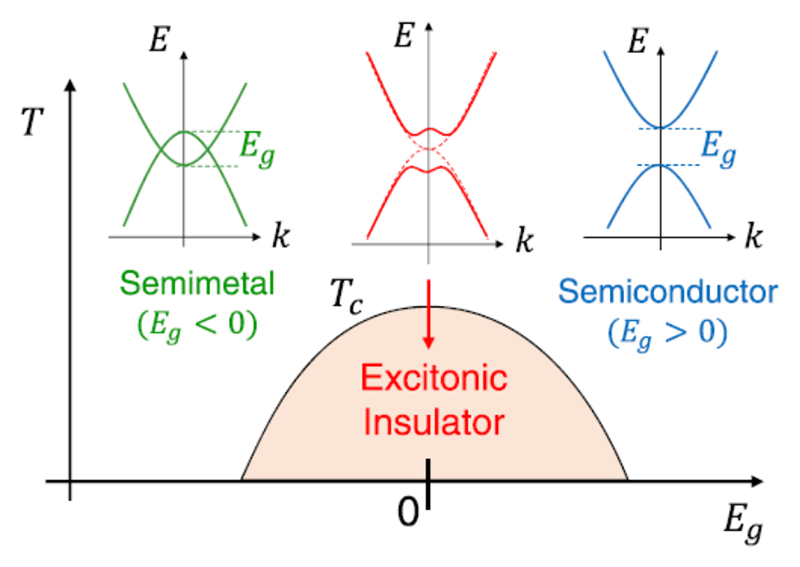
図1　励起子絶縁体（EI）の相図とバンド分散の概念図。Tは温度を、E_gはe-h引力が無い場合の1粒子バンドギャップを表す。

　上記の理論的進展に対して、実験的にEIである可能性が指摘された物質は、長年にわたってごく少数しかなかった。ところが、2009年にWakisaka et al.^[5][5] Y. Wakisaka et al.: Phys. Rev. Lett. 103 (2009) 026402.は、層状物質Ta₂NiSe₅の角度分解光電子分光（ARPES）の結果を報告し、低温で価電子帯の頂上が平坦な分散を持つことなどから、この物質がEIである可能性が高いことを示した。なお、Ta₂NiSe₅においては、T_cは高温での直方晶から低温での単斜晶へと構造相転移が起きる温度に一致する。つまり、より対称性の低い結晶構造への変化がEI相形成につながっているとされた。その後、Lu et al.^[6][6] Y. F. Lu et al.: Nat. Commun. 8 (2017) 14408.はTa₂NiSe₅およびそのS置換系Ta₂Ni(Se, S)₅に対して電気抵抗などの測定を行った。そして彼らは、外部圧力やS置換によって図1のE_gをコントロールすることにより実験的な相図を構築し、図1の理論的相図とconsistentな結果であることから、Ta₂NiSe₅がEIであると結論している。その後、Ta₂NiSe₅の研究は世界的に活発になり、上記の2009年ARPES論文^[5][5] Y. Wakisaka et al.: Phys. Rev. Lett. 103 (2009) 026402.を引用する論文が2019年以降で約150報も出版されている。これらの研究の多くはTa₂NiSe₅がEIであることを支持しているが、一方で、EIであるとの同定を疑問視する論文も複数報告されている。例えば、e-h相関を仮定しなくても平坦なバンドが生じうることや^[7][7] M. D. Watson et al.: Phys. Rev. Res. 2 (2020) 013236.、結晶構造の対称性より、T_c以下の相でのエネルギーギャップは純粋にEI起源にはなり得ず、必ずバンド混成の効果が混ざること^[8][8] A. Subedi: Phys. Rev. Mater 4 (2020) 083601.などが指摘されている。
　このように、Ta₂NiSe₅のギャップ形成機構については、EI形成によるとする考えが有力だが未解決となっている。そこで我々は、Ta₂NiSe₅に外部圧力を加えた上で、赤外分光によって測定した光学伝導度スペクトル［σ(ω)］上に観測されるエネルギーギャップの形状を、圧力（P）と温度（T）の関数として詳しく調べた^[3][3] H. Okamura et al.: Phys. Rev. B 107 (2023) 045141.。高圧下のTa₂NiSe₅の電気抵抗率や結晶構造についてはMatsubayashi et al.^[9][9] K. Matsubayashi et al.: J. Phys. Soc. Jpn. 90 (2021) 074706.やNakano et al.^[10][10] A. Nakano et al.: IUCrJ 5 (2018) 158.によって詳しく調べられており、図2のように高圧下のEI相の消長と結晶構造の変化が密接に関連している。我々の実験では、図2の緑の点で表されたような（P, T）の値で赤外分光実験を行い、エネルギーギャップの変化を調べた。

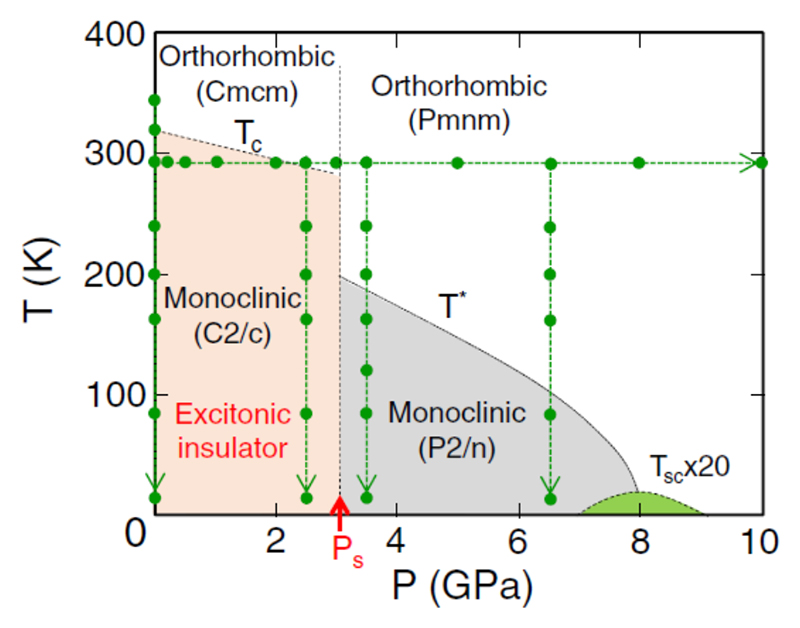
図2　Ta₂NiSe₅の温度（T）－圧力（P）相図^[3][3] H. Okamura et al.: Phys. Rev. B 107 (2023) 045141.。この相図はMatsubayashi et al.^[9][9] K. Matsubayashi et al.: J. Phys. Soc. Jpn. 90 (2021) 074706.による電気抵抗の実験と、Nakano et al.^[10][10] A. Nakano et al.: IUCrJ 5 (2018) 158.による精密構造解析実験により求められた。緑色の点は、我々が光学伝導度の測定を行った（P, T）点を示す。

3. 実験方法
　実験に用いた試料は単結晶試料であり、光沢を持つ自然成長面（ac面）を機械研磨せずそのまま用いて反射率測定を行った。試料への高圧力の印加はダイヤモンド・アンビル・セル（Diamond anvil cell、DAC）を用いて行った。DACは高圧下の様々な実験で用いられているが、本研究では光反射率の測定を行うため、図3の模式図に示すように、試料面をダイヤモンドのキュレット面に密着させ、KBr粉末を圧力媒体として封入した。また、金のフィルムを試料と共にDAC内に封入し、試料上で測定したスペクトルを金フィルム上で測定したスペクトルで割り算することによって反射率スペクトルR(ω)を測定した。Ta₂NiSe₅の実験では、先端平坦面（キュレット面）直径が0.8 mmのダイヤモンドを用いることで、10 GPa（ほぼ10万気圧）までの圧力を印加した。得られたR(ω)から、ダイヤモンドの屈折率を考慮したKramers-Kronig解析^[11][11] H. Okamura: J. Phys.: Conf. Ser. 359 (2012) 012013.を行うことにより、σ(ω)スペクトルを導出した。また、試料の圧力は、試料と共に封入したルビー片を用いてルビー蛍光法で測定した。高圧下の反射分光実験はSPring-8の赤外ビームラインBL43IRにて、遠赤外から中赤外、近赤外領域にかけて（波数200-9000 cm^-1、光子エネルギー0.025-1.1 eV）行った。BL43IRにおける高圧赤外分光実験の詳細については、すでに解説が出版されているので、そちらを参照されたい^{[12, 13]}[12] 岡村英一: 高圧力の科学と技術25 (2015) 11.
[13] H. Okamura et al.: Jpn. J. Appl. Phys. 56 (2017) 05FA11.。

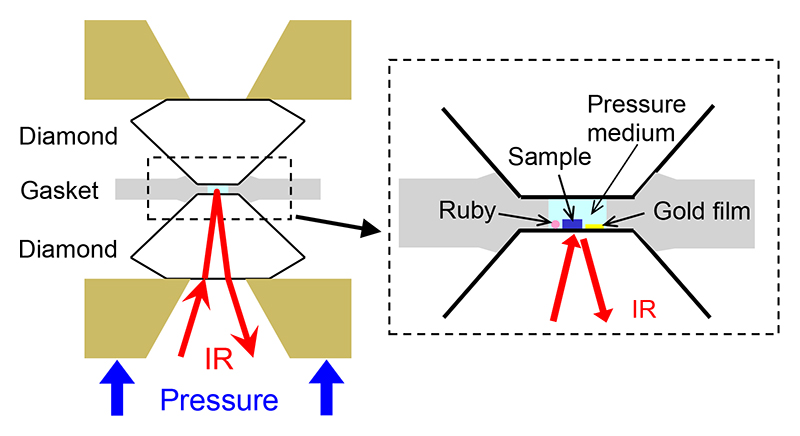
図3　DACを用いた高圧下の反射スペクトル測定の概念図^{[12, 13]}[12] 岡村英一: 高圧力の科学と技術25 (2015) 11.
[13] H. Okamura et al.: Jpn. J. Appl. Phys. 56 (2017) 05FA11.。

4. 実験結果
　図4に、高圧下で測定されたTa₂NiSe₅の赤外反射スペクトルを示す。2.5 GPaにおいては、0.3 eV以下の光子エネルギーでスペクトルが顕著な温度依存性を示しているが、圧力が3.5 GPa、6.5 GPaと増加するに従い、温度依存性が小さくなっていることがわかる。次に図5に、図4の反射スペクトルの解析から求めた光学伝導度スペクトルσ(ω)を、常圧での結果と合わせて示す。図5（a）の常圧データでは、冷却に伴い低エネルギー領域のσ(ω)が減少し、明確なエネルギーギャップが形成されている。ギャップの大きさは、赤い矢印で示されているσ(ω)の立ち上がり（Onset）で定義すると、約0.18 eVである。また、青い矢印で示すように、約0.38 eVに中心を持つ顕著なピークが観測されている。このピークはEI状態の形成のためにバンドが平坦化した結果、吸収端の状態密度が増加した結果と考えられ^[14][14] Y.-S. Seo et al.: Sci. Rep. 8 (2018) 11961.、エネルギーギャップ越しの電子励起における励起子効果を強く反映していると考えられる。次に図5（b）の2.5 GPaでは、冷却に伴い低エネルギー領域のσ(ω)が減少する振る舞いが常圧と同様に見られるが、σ(ω)の減少するエネルギー範囲が、常圧に比べてずっと狭くなっていることがわかる。赤い矢印で示すσ(ω)の立ち上がりは0.06 eVであり、常圧の0.18 eVよりも大幅に小さくなっている。また、常圧に比べて励起子効果を反映したピークが大幅に抑制され、もはやピークの存在自身が不明瞭となっている。すなわち、2.5 GPaではエネルギーギャップはまだ形成されるものの、励起子効果は弱くなっていることを示唆している。この結果は、2.5 GPaという圧力が図2の相図でEI相が消失する直前の圧力領域であることと対応していると考えられる。次に図5（c）の圧力3.5 GPaになると、冷却に伴い低エネルギー領域でのσ(ω)の減少はまだ見られるが、最低測定温度の8 Kになってもσ(ω)がゼロ付近まで落ち込まず、有限な値が残っている。また、8 Kでもゼロエネルギーに向けて増加する成分（図中の青い矢印）が見られるが、これは自由キャリヤによる応答（ドルーデ応答）であると考えられる。つまり、3.5 GPaではE_Fに有限な状態密度があり、エネルギーギャップはもはや不完全なものになっている。この結果より、3.5 GPaではTa₂NiSe₅はもはや絶縁体ではなく、半金属的な電子状態になっていることがわかる。図2の相図では、3.5 GPaはEI相の外に出てすぐの所にあり、まだギャップによる状態密度の落ち込みは残っているが、金属的な電子状態になっているという上述の結果は、この相図とよく対応していると考えられる。最後に図5（d）の圧力6.5 GPaでは、室温から8 Kまでσ(ω)の変化はほとんどなく、低温でのエネルギーギャップは完全に消失しており金属的なスペクトルになっている。

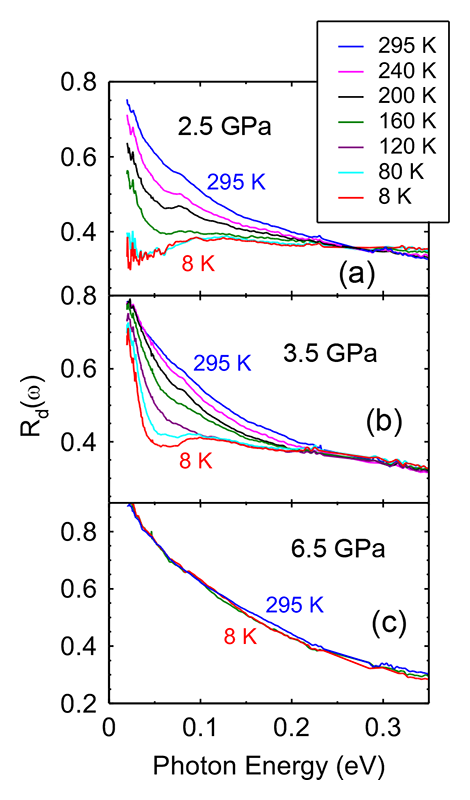
図4　DACを用いて外部圧力（a）2.5 GPa、（b）3.5 GPa、（c）6.5 GPaで測定されたTa₂NiSe₅の赤外反射率スペクトル^[3][3] H. Okamura et al.: Phys. Rev. B 107 (2023) 045141.。

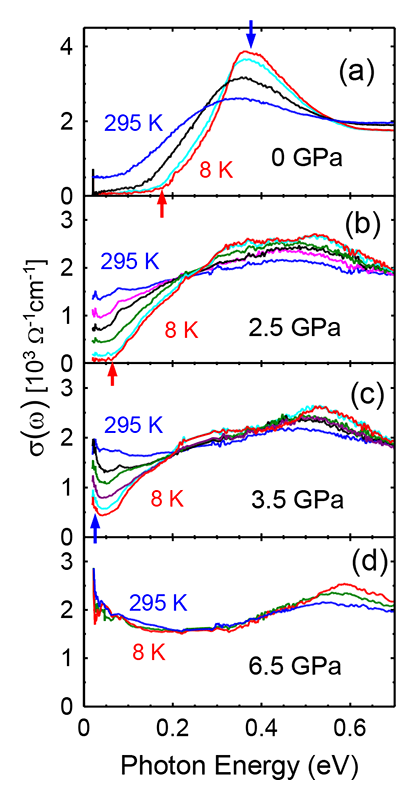
図5　Ta₂NiSe₅の（a）常圧（0 GPa）、（b）2.5 GPa、（c）3.5 GPa、（d）6.5 GPaにおける光学伝導度σ(ω)^[3][3] H. Okamura et al.: Phys. Rev. B 107 (2023) 045141.。各スペクトルの色と測定温度の対応は、図4のそれと同じである。

　さらにエネルギーギャップの振る舞いを詳しく調べるため、常圧および2.5 GPaでのσ(ω)の温度変化をより詳しく表示したものを、図6（a）、（b）にそれぞれ示す。これらのグラフに示すように、σ(ω)においてエネルギーギャップが発達する過程で、スペクトルが直線状に変化している部分の外挿（図中の破線）と横軸との交点を、σ(ω)の立ち上がり（Onset）と見なしている（図中の矢印）。そして、図6（c）では、この立ち上がりのエネルギーを温度Tに対してプロットしている。この立ち上がりをエネルギーギャップの大きさΔと見なすと、ΔとTの間には

（1）

という関係が成り立っているように見える^[14][14] Y.-S. Seo et al.: Sci. Rep. 8 (2018) 11961.。そこで、図6（c）では実験データに加えて、（1）式でα = 2.0、2.5、3.0の場合のグラフをそれぞれ表示している。常圧（0 GPa）では、実験データはα = 2.5に近いがどれとも完全に一致せず、単一のαの値では記述できないように見えるが、先行研究^[14][14] Y.-S. Seo et al.: Sci. Rep. 8 (2018) 11961.で報告されたα = 2.0と近い結果になっている。一方で、圧力2.5 GPaのデータはα = 2.5に近いが、どの値でもほぼ合っているように見える。また、常圧と2.5 GPaでの振る舞いはよく似ており、常圧と2.5 GPaでαの値に違いがあるか否かは、今回のデータの精度では判断できず、両者の温度依存は定性的にほぼ同じと言える。また、図6（c）のデータを（1）式でフィッティングして得られたT_cの値は、常圧でT_c = 328 K、2.5 GPaでT_c = 170 Kである。このうち、常圧でのT_cはEI転移が起きると考えられている構造相転移の温度に等しく、構造相転移と共にEIギャップが成長する描像とconsistentである。一方、2.5 GPaでのT_c = 170 Kは常圧での328 Kの半分程度である。この結果は、2.5 GPaでのギャップ幅0.062 eVが常圧の0.18 eVに比べてずっと小さく、電子の熱励起がより低温にならないと収まらないことに起因すると考えられる。（ボルツマン定数をk_Bとすると、熱エネルギーk_BTは80 Kで0.0069 eV、160 Kで0.014 eVであり、ギャップ幅0.062 eVの半分で与えられる活性化エネルギーに対する割合はそれぞれ0.22、0.44である。この割合が0.2以下で熱励起が急激に減少するため、160 Kから80 Kへの冷却でσ(ω)のギャップが明確になることとconsistentである。）

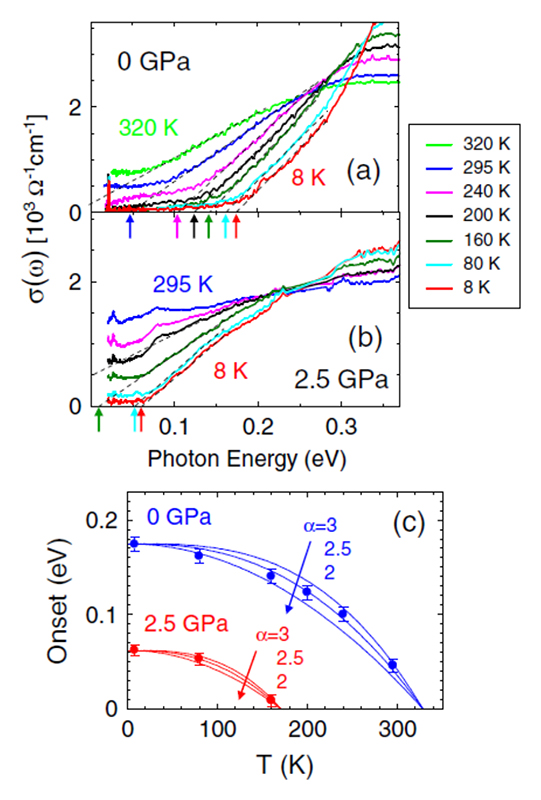
図6　Ta₂NiSe₅のσ(ω)におけるエネルギーギャップの詳しい解析^[3][3] H. Okamura et al.: Phys. Rev. B 107 (2023) 045141.。（a）常圧（0 GPa）および（b）2.5 GPaにおけるσ(ω)の立ち上がりの見積もり。矢印は立ち上がりの位置を示す。（c）立ち上がり（Onset）の温度依存性。αについては本文参照のこと。

　上述したように、2.5 GPaにおけるギャップ幅0.062 eVは、常圧でのギャップ幅0.18 eVに比べてずっと小さい。一方、構造相転移がおきる温度は常圧での328 Kから2.5 GPaでの約290 Kまで、1割程度しか下がっていない。すなわち、加圧によるギャップ幅の抑制は、加圧による構造相転移の抑制と比べてずっと強くなっている。つまり、加圧によるギャップ幅の減少は、構造相転移温度のそれとスケールしておらず、この結果は2.5 GPaでのギャップが純粋にEI由来ではないことを示唆するように見える。さらに、EI相のすぐ外側に出た3.5 GPaではギャップが埋まって不完全になる結果［図5（c）］と合わせると、2.5 GPaで生き残っているギャップはバンド混成による寄与で、常圧のギャップ幅（0.18 eV）から2.5 GPaのギャップ幅（0.062 eV）へ減少した分が励起子効果と関係しているとの推測もできる。実際はバンド混成によるギャップも圧力に依存するはずであり、現実の状況は非常に複雑である。今後、より詳しく実験データを理解するためには、励起子相関とバンド混成の両方の圧力効果を取り込んだギャップ形成に対する、ミクロな視点からのモデルが必要と考えられる。

5. おわりに
　筆者らが最近SPring-8の赤外ビームラインBL43IRを利用して行った、EI候補物質Ta₂NiSe₅に関する研究結果を報告した。特に、10 GPaにおよぶ高圧下かつ低温での赤外分光実験から光学伝導度σ(ω)を導出し、常圧で明確に観測されているエネルギーギャップが、圧力によって抑制されていく様子を詳しく調べた結果について解説した。高圧力の印加は、結晶における原子間隔をクリーンに（化学置換によって結晶を乱すことなく）、かつ連続的に制御できる有用な実験方法であり、高圧下で様々な興味深い物性が見いだされている。物性の起源となるミクロな電子状態は、例えばARPESやSTM（走査トンネル顕微鏡）などを用いて盛んに研究されているが、これらの手法は高圧セルに封入された試料に対して行うのは技術的に困難である。一方、本研究で用いた高圧下の赤外分光手法によれば、高圧下でE_F近傍の電子状態を1 meV程度の高いエネルギー分解能で調べることができる。従って、今後も様々な物質系に対してこの手法を用いて、高圧下で現れる特異な電子状態の研究が進展することが期待される。
　本研究はBL43IRを用いて、課題番号2013A1085、2015B1698、2016A1166、2017A1163、2017A1164の下で行われました。ビームラインサイエンティストの池本夕佳氏、森脇太郎氏、早稲田大学の溝川貴司氏を始めとする共同研究者の方々に深く感謝申し上げます。

参考文献
[1] S. Kimura and H. Okamura: J. Phys. Soc. Jpn. 82 (2013) 021004.
[2] 岡村英一他: 日本赤外線学会誌28 (2018) 48.
[3] H. Okamura et al.: Phys. Rev. B 107 (2023) 045141.
[4] 太田幸則他: 固体物理52 (2017) 119.
[5] Y. Wakisaka et al.: Phys. Rev. Lett. 103 (2009) 026402.
[6] Y. F. Lu et al.: Nat. Commun. 8 (2017) 14408.
[7] M. D. Watson et al.: Phys. Rev. Res. 2 (2020) 013236.
[8] A. Subedi: Phys. Rev. Mater 4 (2020) 083601.
[9] K. Matsubayashi et al.: J. Phys. Soc. Jpn. 90 (2021) 074706.
[10] A. Nakano et al.: IUCrJ 5 (2018) 158.
[11] H. Okamura: J. Phys.: Conf. Ser. 359 (2012) 012013.
[12] 岡村英一: 高圧力の科学と技術25 (2015) 11.
[13] H. Okamura et al.: Jpn. J. Appl. Phys. 56 (2017) 05FA11.
[14] Y.-S. Seo et al.: Sci. Rep. 8 (2018) 11961.

岡村　英一　OKAMURA Hidekazu
徳島大学
大学院社会産業理工学研究部　理工学域応用化学系
〒770-8506　徳島県徳島市南常三島町2-1
TEL : 088-656-9444
e-mail : ho@tokushima-u.ac.jp