Volume 29, No.1 Pages 6 - 13

1. 研究背景
　強磁性材料がもつ「不揮発性」「再構成可能」という特長と機能を「高速度演算」を担う半導体集積回路に融合することにより、高速かつ低消費電力で動作するスピン機能半導体デバイスを実現することが期待されている^[1][1] I. Žutić, J. Fabian, and S. Das Sarma: Rev. Mod. Phys. 76 (2004) 323-410.。このようなスピンデバイスの出力は強磁性体の磁化（スピン）の向きで制御されるが、磁気ランダムアクセスメモリ（MRAM）を代表とする最も研究が進み実用化されているスピンデバイスでは、磁化反転は速くても数ナノ秒（ns）程度であり、従来の半導体トランジスタ（MOSFET）の動作速度より一桁程度も遅い。また、MRAMでは磁化を反転させ書き込みを行うために電流駆動による磁化制御法が用いられているが、10⁶～10⁷ A/cm²という極めて高い電流密度を必要とするため、大量の電力を消費する。将来のスピンデバイスでは、これらの問題を解決し高速かつ低消費電力で磁化を制御する方法を確立する必要がある。特に、スピンデバイスを現在のCMOSの動作速度を超えるTHz周波数で動作できるようになることが望ましく^[2][2] K. A. Mistry: 2007 IEEE Intl. Electron Devices Meeting. (2007) 247-250.、そのためには強磁性体の磁化をサブピコ秒（サブps）の時間スケールで制御することが必要になる。さらに、基礎研究の観点から、このような超高速時間スケールでスピンダイナミクス現象を調べることにより、交換相互作用やスピン軌道相互作用など、強磁性体におけるさまざまな磁気結合の基礎となるメカニズムを明らかにすることができると期待される。
　これまでの超高速スピンダイナミクスの研究では、磁性材料を励起するために強い強度を持つfsパルスレーザを照射し（この操作は光ポンピングと呼ばれる）、それと同期した別のレーザパルスで磁化の変化を観察する（この操作はプローブと呼ばれる）ポンプ・アンド・プローブ法が一般的に使用されている。その際、電荷、スピン、格子振動（フォノン）の間で非平衡な熱的相互作用と熱によらない相互作用が発生する^[3][3] A. Kirilyuk, A. V. Kimel, and T. Rasing: Rev. Mod. Phys. 82 (2010) 2731-2784.。これらの過程によって、消磁現象^[4-13][4] E. Beaurepaire, J. -C. Merle, A. Daunois and J. -Y. Bigot: Phys. Rev. Lett. 76 (1996) 4250.
[5] J. Hohlfeld, E. Matthias, R. Knorren and K. H. Bennemann: Phys. Rev. Lett. 78 (1997) 4861.
[6] A. Scholl, L. Baumgarten, R. Jacquemin and W. Eberhardt: Phys. Rev. Lett. 79 (1997) 5146.
[7] B. Koopmans, M. van Kampen, J. T. Kohlhepp, and W. J. M. de Jonge: Phys. Rev. Lett. 85 (2000) 844.
[8] H.-S. Rhie, H. A. Dürr, and W. Eberhardt: Phys. Rev. Lett. 90 (2003) 247201.
[9] M. Lisowski, P. A. Loukakos, A. Melnikov, I. Radu, L. Ungureanu et al.: Phys. Rev. Lett. 95 (2005) 137402.
[10] M. Cinchetti, M. Sanchez Albaneda, D. Hoffmann, T. Roth, J. P. Wustenberg et al.: Phys. Rev. Lett. 97 (2006) 177201.
[11] C. Stamm, T. Kachel, N. Pontius, R. Mitzner, T. Quast et al.: Nature Mater. 6 (2007) 740.
[12] E. Carpene, E. Mancini, C. Dallera, M. Brenna, E. Puppin et al.: Phys. Rev. B 78 (2008) 174422.
[13] E. A. Mashkovich, K.A. Grishunin, H. Munekata, & A.V. Kimel: Appl. Phys. Lett. 117 (2020) 122406.、磁気歳差運動^[14-19][14] G. Ju, A. V. Nurmikko, R. F. Farrow, R. F. Marks, M. J. Carey et al.: Phys. Rev. B 58 (1998) R11857.
[15] L. H. F. Andrade, A. Laraoui, M. Vomir, D. Muller, J.-P. Stoquert et al.: Phys. Rev. Lett. 97 (2006) 127401.
[16] D. M. Wang, Y. H. Ren, X. Liu, J. K. Furdyna, M. Grimsditch et al.: Phys. Rev. B 75 (2007) 233308.
[17] Y. Hashimoto, S. Kobayashi and H. Munekata: Phys. Rev. Lett. 100 (2008) 067202.
[18] E. Rozkotová, P. Němec, P. Horodyská, D. Sprinzl, F. Trojánek et al.: Appl. Phys. Lett. 92 (2008) 122507.
[19] J. Qi, Y. Xu, A. Steigerwald, X. Liu, J. K. Furdyna et al.: Phys. Rev. B 79 (2009) 085304.、光照射による磁化反転^[20-27][20] Y. Yang, R. B. Wilson, J. Gorchon, C. –H. Lambert, S. Salahuddin et al.: Sci. Adv. 3 (2017) e1603117.
[21] C. D. Stanciu, F. Hansteen, A. V. Kimel, A. Kirilyuk, A. Tsukamoto et al.: Phys. Rev. Lett. 99 (2007) 047601.
[22] S. Mangin, M. Gottwald, C-H. Lambert, D. Steil, V. Uhlíř et al.: Nat. Mater. 13 (2014) 286-292.
[23] C-H. Lambert, S. Mangin , B. S. D. Ch. S. Varaprasad, Y. K. Takahashi, M. Hehn et al.: Science 345 (2014) 1337-1340.
[24] C. Banerjee, N. Teichert, K. E. Siewierska, Z. Gercsi, G. Y. P. Atcheson et al.: Nat. Commun. 11 (2020) 1-6.
[25] I. Radu, K. Vahaplar, C. Stamm, T. Kachel, N. Pontius et al.: Nature 472 (2011) 205-208.
[26] T. A. Ostler, J. Barker, R.F.L. Evans, R.W. Chantrell, U. Atxitia et al.: Nat. Commun. 3 (2012) 666.
[27] K. Yamamoto, S. El Moussaoui, Y. Hirata, S. Yamamoto, Y. Kubota et al.: Appl. Phys. Lett. 116 (2020) 172406.、磁化の増大^{[28, 29]}[28] J. Wang, I. Cotoros, K. M. Dani, X. Liu, J. K. Furdyna, and D. S. Chemla: Phys. Rev. Lett. 98 (2007) 217401.
[29] F. Liu, T. Makino, T. Yamasaki, K. Ueno, A. Tsukazaki et al.: Phys. Rev. Lett. 108 (2012) 257401.、サブ格子間におけるスピントランスファー^[30-35][30] D. Rudolf, C. La-O-Vorakiat, M. Battiato, R. Adam, J. M. Shaw et al.: Nature Commun. 3 (2012) 1037.
[31] P. Elliott, T. Müller, J. K. Dewhurst, S. Sharma and E. K. U. Gross: Sci. Rep. 6 (2016) 38911.
[32] F. Siegrist, J. A. Gessner, M. Ossiander, C. Denker, Y.-P. Chang et al.: Nature 571 (2019) 240-244.
[33] P. Tengdin, C. Gentry, A. Blonsky, D. Zusin, M. Gerrity et al.: Sci. Adv. 6 (2020) eaaz1100.
[34] M. Hofherr, S. Häuser, J. K. Dewhurst, P. Tengdin, S. Sakshath et al.: Sci. Adv. 6 (2020) eaay8717.
[35] D. Steil, J. Walowski, F. Gerhard, T. Kiessling, D. Ebke et al.: Phys. Rev. Research 2 (2020) 023199.、磁気相転移^[36-38][36] J. U. Thiele, M. Buess and C. H. Back: Appl. Phys. Lett. 85 (2004) 2857-2859.
[37] G. Ju, J. Hohlfeld, B. Bergman, R. J. M. van de Veerdonk, O. N. Mryasov et al.: Phys. Rev. Lett. 93 (2004) 197403.
[38] G. Li, R. Medapalli, J. H. Mentink, R. V. Mikhaylovskiy, T. G. H. Blank et al.:Nature Commun. 13 (2022) 2998.など、金属、半導体、絶縁体のさまざまな強磁性材料における超高速現象、ときにはサブpsの磁化制御が報告されている。光は材料のスピン自由度とほとんど相互作用しないが、強いfsレーザパルスを照射すれば瞬時に大量の光キャリア（正孔、電子）を強磁性材料中に生成することができる。これにより電子温度が上昇し、その結果、電荷－スピン、電子－フォノン、電子－マグノンの相互作用を介してスピン温度と格子温度が上昇し、磁化の変化が起こると考えられる^[3][3] A. Kirilyuk, A. V. Kimel, and T. Rasing: Rev. Mod. Phys. 82 (2010) 2731-2784.。レーザ光のエネルギーが物質中のバンド間遷移と共鳴すると、レーザパルス照射により直接d軌道またはf軌道のスピン偏極バンドにキャリアを励起し、瞬間的な磁化増大^[29][29] F. Liu, T. Makino, T. Yamasaki, K. Ueno, A. Tsukazaki et al.: Phys. Rev. Lett. 108 (2012) 257401.またはサブ格子間のスピントランスファー^[30-35][30] D. Rudolf, C. La-O-Vorakiat, M. Battiato, R. Adam, J. M. Shaw et al.: Nature Commun. 3 (2012) 1037.
[31] P. Elliott, T. Müller, J. K. Dewhurst, S. Sharma and E. K. U. Gross: Sci. Rep. 6 (2016) 38911.
[32] F. Siegrist, J. A. Gessner, M. Ossiander, C. Denker, Y.-P. Chang et al.: Nature 571 (2019) 240-244.
[33] P. Tengdin, C. Gentry, A. Blonsky, D. Zusin, M. Gerrity et al.: Sci. Adv. 6 (2020) eaaz1100.
[34] M. Hofherr, S. Häuser, J. K. Dewhurst, P. Tengdin, S. Sakshath et al.: Sci. Adv. 6 (2020) eaay8717.
[35] D. Steil, J. Walowski, F. Gerhard, T. Kiessling, D. Ebke et al.: Phys. Rev. Research 2 (2020) 023199.を引き起こす。場合によっては、レーザパルスの電場が材料の磁気特性に直接影響を与える^[39-42][39] C. Vicario, C. Ruchert, F. Ardana-Lamas, P. M. Derlet, B. Tudu et al.: Nat. Photonics 7 (2013) 720.
[40] S. Bonetti, M. C. Hoffmann, M.-J. Sher, Z. Chen, S.-H. Yang et al.: Phys. Rev. Lett. 117 (2016) 087205.
[41] T. Kampfrath, K. Tanaka, and K. A. Nelson: Nat. Photonics 7 (2013) 680.
[42] T. Ishii, H. Yamakawa, T. Kanaki, T. Miyamoto, N. Kida et al.: Appl. Phys. Lett. 114 (2019) 062402.。これらの実証実験は、光で制御する超高速スピンエレクトロニクスに応用できると期待される。一方、このような超高速スピンダイナミクスを、すでに確立している半導体デバイス技術および大規模集積化が可能な現在のCMOS集積回路に実装することが強く望まれる。しかし、CMOSの基本動作であるゲート電圧による電界効果では、光ポンピングのようにキャリア密度を瞬時に大幅に変えたり、超高速の時間スケールでバンド間の遷移を引き起こしたりすることは不可能である。本研究では、波動関数工学と呼ばれるサブps磁化操作の新しい手法を、強磁性半導体を含む半導体量子井戸ヘテロ構造を用いて実証することを目指した。この手法では、フェルミ準位E_Fにおけるs（またはp）電子の空間分布（波動関数によって決める）のみを制御し、電子濃度の変化を必要としないため、ゲート電圧による制御操作と整合性があり、将来の超高速スピンエレクトロニクスへの応用が期待される。
　超高速スピンダイナミクスについてこれまで研究されてきた材料の中で、強磁性半導体（Ferromagnetic semiconductor、FMS）は多くの重要な利点を有する。FMSは、通常のIV族、III-V族、またはII-VI族非磁性半導体に局在スピンの役割を果たすd軌道またはf軌道を持つ磁性元素（Mn、Fe、Euなど）を数％程度以上添加した混晶半導体である^{[43, 44]}[43] H. Ohno: Science 281 (1998) 951-956.
[44] M. Tanaka, S. Ohya, and P. N. Hai: Appl. Phys. Rev. 1 (2014) 011102.。これらの局在スピン（dまたはf電子）は、s-d（f）またはp-d（f）交換相互作用を介して遍歴キャリア（sまたはp電子）と強く結合することによって、強磁性秩序が成立すると考えられる^[45][45] T. Dietl, H. Ohno, F. Matsukura, J. Cibert and D. Ferrand: Science 287 (2000) 1019-1022.。FMSでは、強磁性金属とは異なり局在スピンとキャリアが明確に分離されているため、スピン－キャリア相互作用が引き起こす様々な物理現象を解明するという点で理想的な材料系である。さらに、FMSは比較的小さいキャリア密度（10¹⁸～10²⁰ cm^-3程度）と長いThomas-Fermiスクリーニング長により、レーザ光源を用いた光ポンピングまたはゲート電界を用いた電気的なキャリア特性の制御が可能である。FMSの強磁性を超高速で増大させた実験例として、光ポンピングによってp型(Ga,Mn)Asの磁化を増大させた報告があり^[28][28] J. Wang, I. Cotoros, K. M. Dani, X. Liu, J. K. Furdyna, and D. S. Chemla: Phys. Rev. Lett. 98 (2007) 217401.、その時間スケールは100 psであった。(Ga,Mn)Asのp-d交換相互作用の大きさは約1 eVであるため、ハイゼンベルクの不確定性原理によるキャリアの濃度変化に対する磁化変化の最短時間は1 fs程度と考えられ、上記の100 psという時間ははるかに長い。この磁化増大が遅い理由として、(Ga,Mn)Asの磁化を変えるにはE_Fでの正孔密度の大きな変化（～10²⁰ cm^-3）が必要であり、これらの正孔は高いエネルギーバンドに光生成された光キャリアがゆっくり緩和した後にE_F位置の状態に供給されるためと考えられる。したがって、より高速で磁化を制御するためには、FMSにおけるキャリアとスピンの相互作用の物理を明らかにして、キャリア特性をサブpsで変調するための新しい手法を開発する必要がある。
　さまざまなFMSの中で、III-V族ベースFMSは最も広く研究され半導体デバイスとも整合性が良い。中でも我々が開発した(In,Fe)Asは最初の電子誘起n型FMSでありいくつかの有用な特長を有している^[46-50][46] P. N. Hai, L. D. Anh, S. Mohan, T. Tamegai, M. Kodzuka et al.: Appl. Phys. Lett. 101 (2012) 182403.
[47] P. N. Hai, L. D. Anh and M. Tanaka: Appl. Phys. Lett. 101 (2012) 252410.
[48] L. D. Anh, P. N. Hai and M. Tanaka: Nature Commun. 7 (2016) 13810.
[49] L. D. Anh, P. N. Hai and M. Tanaka: Appl. Phys. Lett. 104 (2014) 042404.
[50] L. D. Anh, P. N. Hai, Y. Kasahara, Y. Iwasa and M. Tanaka: Phys. Rev. B 92 (2015) 161201(R).
。(In,Fe)Asの伝導帯下端に存在する電子キャリアは40 nmもの長いコヒーレンス長を持つ^[49][49] L. D. Anh, P. N. Hai and M. Tanaka: Appl. Phys. Lett. 104 (2014) 042404.。したがって、図1(a)に示すような薄い(In,Fe)As/InAs二層構造は、電子キャリアの波動関数が二層全体に広がって表面量子井戸を形成する（図1(b)）。この二次元（2D）電子をもつ強磁性半導体量子井戸構造の重要な特徴の1つは、キュリー温度（T_C）などの磁気特性が、波動関数と局在スピン（Fe）の間の空間的重なりによって決定されることである^[49-51][49] L. D. Anh, P. N. Hai and M. Tanaka: Appl. Phys. Lett. 104 (2014) 042404.
[50] L. D. Anh, P. N. Hai, Y. Kasahara, Y. Iwasa and M. Tanaka: Phys. Rev. B 92 (2015) 161201(R).
[51] B. Lee, T. Jungwirth, and A. H. MacDonald: Phys. Rev. B 61 (2000) 15606.。したがって、波動関数のピーク位置と形状を制御することにより、量子井戸に余分なキャリアを注入しなくても、(In,Fe)As/InAs量子井戸の磁気特性を効果的に制御できる。波動関数工学と呼ばれるこの新しい手法は、キャリア蓄積プロセスがなく、量子井戸内で電子波動関数をわずか数ナノメートル移動させるだけであるため、消費電力が極めて低く^[50][50] L. D. Anh, P. N. Hai, Y. Kasahara, Y. Iwasa and M. Tanaka: Phys. Rev. B 92 (2015) 161201(R).、動作速度が非常に速くなることが期待される。本研究では、この超高速波動関数工学がfsパルスレーザを使用して実現可能であり、これにより(In,Fe)As/InAs量子井戸の磁化がサブpsの時間で増大することを示す。

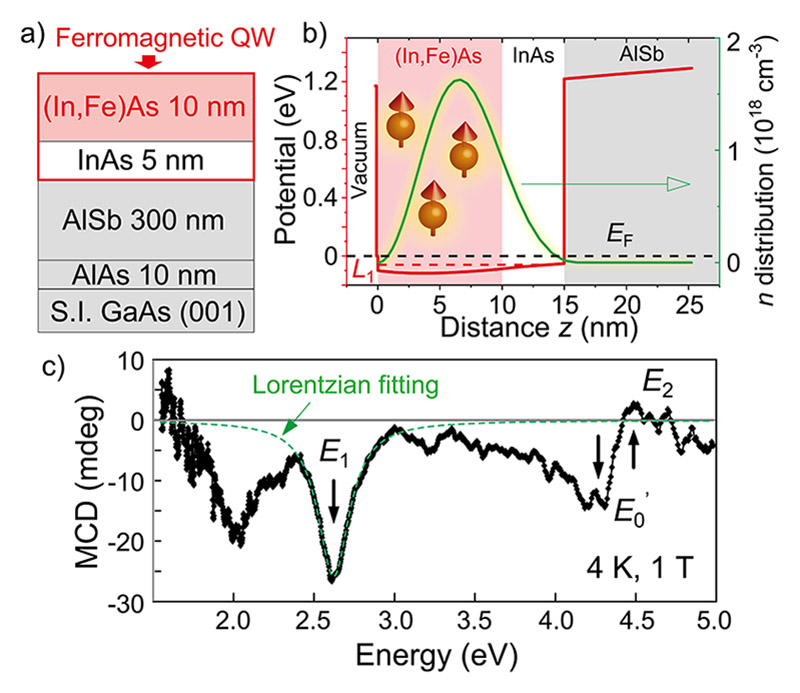
図1　(a) 本研究で用いた試料構造。(b) 試料における伝導帯のポテンシャルプロファイルと電子分布。(In,Fe)As（10 nm、Fe濃度8％）/InAs（5 nm）から成る二層構造は、電子キャリアの波動関数が二層全体に広がって表面量子井戸（QW）を形成。(c) 4 K、1 Tで測定したMCDスペクトル。InAsの特異点エネルギーE₁での光学遷移に対応する2.626 eVで大きなピークを示す。図は文献[63]より改変転載。

2. 実験結果
　本研究で用いる試料構造は、半絶縁GaAs（001）基板上に分子線エピタキシー法（Molecular Beam Epitaxy、MBE）を用いて成長した、表面から(In,Fe)As（10 nm、Fe濃度8％）/InAs（5 nm）/AlSb（300 nm）/AlAs（5 nm）/GaAsで構成される単結晶ヘテロ構造である（図1(a)）。図1(b)に示すように、InAs/AlSb界面の1.3 eVの伝導帯オフセットと(In,Fe)As表面の真空ポテンシャル（4.2 eV）がポテンシャル障壁の役割を果たし、電子キャリアを(In,Fe)As/InAs二層構造から成る量子井戸に閉じ込める。(In,Fe)As/InAs量子井戸の磁気特性を、可視光磁気円二色性（Magnetic circular dichroism、MCD）分光法を使用して評価した。低温（5 K）から様々な温度において(In,Fe)As/InAs量子井戸の磁化曲線を反映するMCD信号の磁場依存性（MCD－H曲線）のアロットプロットから、(In,Fe)As/InAs量子井戸のキュリー温度（T_C）は約17 Kであると見積もられる。図1(c)に示すMCDスペクトルは、InAsの特異点エネルギーE₁での光学遷移に対応する2.626 eVで大きなピークを示す。このE₁ピークは、バルク状態に近い厚い(In,Fe)As試料のピーク（2.610 eV）から0.016 eVだけ高いエネルギーの方にシフトしている。これは、(In,Fe)As/InAs量子井戸における量子化によるバンドギャップの増大を反映している^{[49, 50]}[49] L. D. Anh, P. N. Hai and M. Tanaka: Appl. Phys. Lett. 104 (2014) 042404.
[50] L. D. Anh, P. N. Hai, Y. Kasahara, Y. Iwasa and M. Tanaka: Phys. Rev. B 92 (2015) 161201(R).。
　(In,Fe)As/InAs量子井戸の磁化を調べるために、SACLAの直線偏光の軟X線自由電子レーザ（X-ray free electron laser、XFEL）ビームを使用して、FeのM吸収端と共鳴する52 eVエネルギーでX線磁気光学カー効果（XMOKE）測定を行った^[52-54][52] T. Ishikawa et al.: Nat. Photonics 6 (2012) 540.
[53] S. Owada, K. Togawa, T. Inagaki, T. Hara, T. Tanaka et al.: J. Synchrotron Radiat. 25 (2018) 282.
[54] Sh. Yamamoto, M. Taguchi, M. Fujisawa, R. Hobara, S. Yamamoto et al.: Phys. Rev. B 89 (2014) 064423.。同じ試料の2枚のサンプル（AおよびB）を2つのネオジム（Nd）磁石（磁場の大きさμ₀H = 0.4 Tおよび - 0.4 T）上に接着し、Heフロークライオスタットのコールドフィンガーに設置した。続いて図2(a)に示すように、(In,Fe)As/InAs量子井戸から反射された後のXFELビームのカー回転角θ_Kを、多層膜ミラーとマイクロチャネルプレート（MCP）で構成される回転アナライザーエリプソメータ―によって検出した。多層膜ミラーとMCPは、サンプル軸に対して角度χだけ一緒に回転される。反射するXFELビームの強度IはI(χ)∝cos² (θ_K －χ)のようにχの関数として変化するため、アナライザーとXFELビームの偏光面が平行/垂直のときに最大/最小に達する^[54][54] Sh. Yamamoto, M. Taguchi, M. Fujisawa, R. Hobara, S. Yamamoto et al.: Phys. Rev. B 89 (2014) 064423.。図2(b)は、Nd磁石からμ₀H = -0.4 Tを垂直に印加しながら300 K（オレンジ色の丸）と9 K（緑色の丸）でサンプルBについて測定した強度I(χ)を示しており、どちらの曲線も関数cos² (θ_K - χ)によくフィッティングできている。9 Kでの曲線は300 Kでの曲線から1.15°だけ右にシフトしている。これは、温度の低下に伴って(In,Fe)As/InAs量子井戸の強磁性秩序が成立するためXFELビームのカー回転角θ_Kが増大することで理解できる。さらに、サンプルAとBについて、両方とも9 Kで測定した強度I(χ)を図2(c)で比較している。サンプルA（μ₀H = 0.4 T）の曲線は左に、サンプルB（μ₀H = -0.4 T）の曲線は右にシフトし、それぞれ反対の磁化方向を持つことを反映している。2つのθ_K値の差は5.40°であり、そこから(In,Fe)As/InAs磁化に対応するXFELビームのカー回転角は2.70°であると見積もられる。磁場を反転することによって得られるθ_Kの変化は、温度を下げた場合に比べて2倍大きい。これらの結果はXMOKE測定の有効性を示すものである。

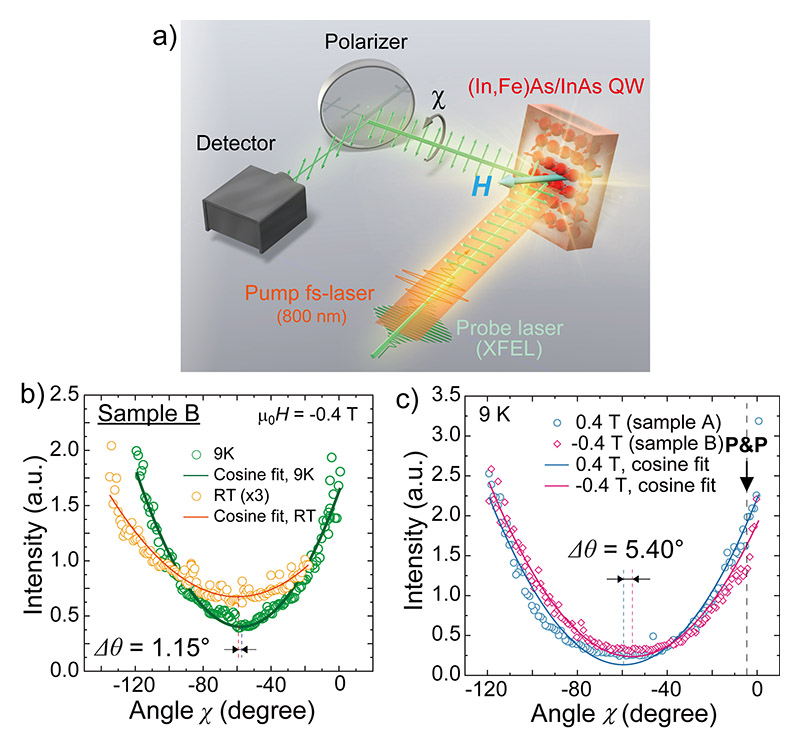
図2　(a) 測定系の概念図。(b) μ₀H = -0.4 Tを垂直に印加しながら300 K（オレンジ色の円）と9 K（緑色の円）でサンプルBについて測定した強度I(χ)。(c) サンプルAとBについて、両方とも9 Kで測定された強度I(χ)の比較。図は文献[63]より改変転載。

　(In,Fe)As/InAs量子井戸のスピンダイナミクスを研究するために、ポンプ・アンド・プローブ測定を実施した。fsパルスレーザ（波長793 nm、パルス幅30 fs、エネルギー169 μJ）を使用してフェルミ面近くのs、p電子系を励起し、XFELビームを使用してFeの局在スピンの応答を調べた。異なるフォトンエネルギーを持つ別々のポンプレーザ光源とプローブレーザ光源を利用することにより、(In,Fe)As/InAs量子井戸におけるスピン・キャリア相互作用の超高速ダイナミクスを捉えることができる。時間分解測定では、回転アナライザーの角度χは -5°に固定し、温度は9 Kとした。図2(c)の結果から、サンプルAとBにおいて磁化Mが増大すると、I(χ)曲線がそれぞれさらに左と右にシフトする。その結果、図3(a)の挿入図に示すように、サンプルAの場合、磁化の向きに応じて強度I（χ = -5°）が増加する。図3(a)の上部パネルに示すように、赤外レーザパルスでサンプルAをポンプすると、XFELビーム強度は600 fsの時間スケールで瞬時に増加（2.8から3.4）（領域I）し、その次の数psで徐々に飽和してから減少した（領域II）。これらの結果は、サンプルAの(In,Fe)As/InAs量子井戸の磁化Mが1 ps未満で増大することを示している。比較のために、サンプルBについても同様の実験を行った。ここで、図3(a)の下のパネルに示すように、Mは反対方向に向いている場合、XFELビーム強度は最初が1 ps（領域I）で3.5から3に急速に減少し、次の60 psで5～6に増加した後120 psでゆっくりと初期値に戻った（図3(b)）を参照）。サンプルAとBのXFELビーム強度の変化の符号が反対になっていることから、その変化が実際に(In,Fe)As/InAs量子井戸の磁化Mの増大から生じていることを示しており、ポンプレーザパルスの光磁気効果に関係する原因を除外できる。照射により、磁化Mは600 fsの超高速の時間スケールで増大し、その後平衡に戻る前に40 psにわたってゆっくりと減少する。この緩やかな消磁現象は、サンプル温度を一時的に上昇させるポンプレーザパルスの熱効果によるものと考えられる。本研究で観測した(In,Fe)As/InAs量子井戸の超高速磁化増大（～600 fs）は、これまでに報告された強磁性半導体の磁化制御の中で最速の値である。

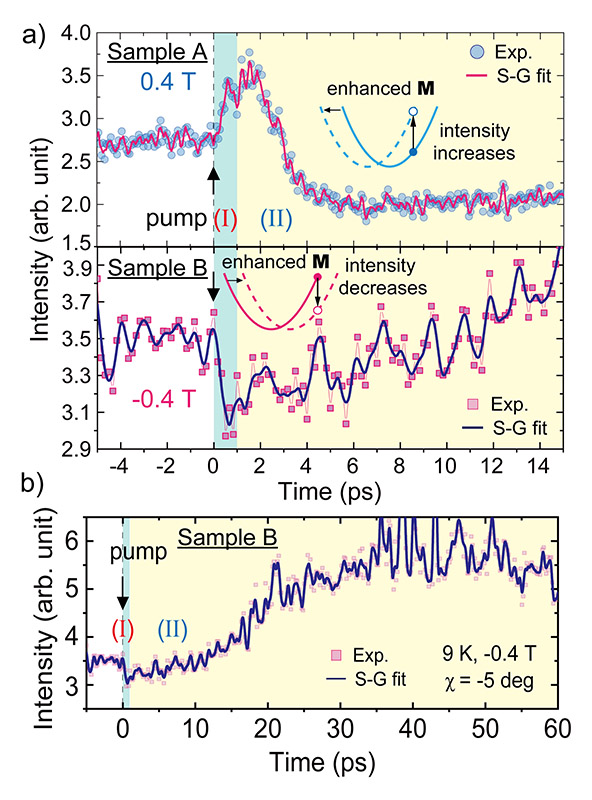
図3　(a) （上）μ₀H = 0.4 Tと（下）μ₀H = -0.4 Tを垂直に印加したサンプルAとBを赤外レーザパルスでポンプしたときのXFELビーム強度の時間変化。600 fsの時間スケールで瞬時に磁化が増大したことが分かった（領域I）。(b) サンプルBの反射したXFELビーム強度の時間変化をより広い範囲で示す図。測定温度は9 Kである。図は文献[63]より改変転載。

3. 超高速磁化増大の機構
　次に、(In,Fe)As/InAs量子井戸で観察された磁化増大の考えられるメカニズムについて考察する。キャリア誘起FMSでは、磁化増大の考えられる原因の1つは、フェルミ準位付近のキャリア密度（(In,Fe)Asの場合はn型なので電子）の増加である。フォトンエネルギー1.55 eV（波長798 nm）のfsレーザパルスを照射すると、(In,Fe)As/InAs量子井戸内に大量の光キャリア（電子と正孔）が瞬時に生成される。しかし、生成された光電子は伝導帯底部より1 eVも高いバンド中に存在するため、伝導帯下端の直下に形成されるFeの不純物バンドのd電子スピンとのs-d交換相互作用に直接関与することができない^{[48, 55]}[48] L. D. Anh, P. N. Hai and M. Tanaka: Nature Commun. 7 (2016) 13810.
[55] M. Kobayashi, L. D. Anh, J. Minár, W. Khan, S. Borek et al.: Phys. Rev. B 103 (2021) 115111.（図4(a)参照）。伝導帯下端までの光電子の緩和には、一般的には数十psが必要である^[3][3] A. Kirilyuk, A. V. Kimel, and T. Rasing: Rev. Mod. Phys. 82 (2010) 2731-2784.。したがって、光キャリア生成だけでは磁化Mのサブps増大を説明できない。さらに、フェルミ準位より上には少数スピンのFe関連不純物バンドしか存在せず^[55][55] M. Kobayashi, L. D. Anh, J. Minár, W. Khan, S. Borek et al.: Phys. Rev. B 103 (2021) 115111.、これらのd軌道不純物バンドへの電子の励起は、試料の磁気モーメントの減少につながると考えられる。これは明らかに実験観察と一致しない。一方、AlSbバッファ層ではΓ点でのバンドギャップ（2.2 eV）が大きいためポンプレーザでは光キャリアは生成されず、下層のAlSb層からの超拡散電流による機構^[56-60][56] A. Melnikov, I. Razdolski, T. O. Wehling, E. Th. Papaioannou, V. Roddatis et al.: Phys. Rev. Lett. 107 (2011) 076601.
[57] N. Bergeard, M. Hehn, S. Mangin, G. Lengaigne, F. Montaigne et al.: Phys. Rev. Lett. 117 (2016) 147203.
[58] M. Hofherr, P. Maldonado, O. Schmitt, M. Berritta, U. Bierbrauer et al.: Phys. Rev. B 96 (2017) 100403.
[59] A. Eschenlohr, M. Battiato, P. Maldonado, N. Pontius et al.: Nat. Mater. 12 (2013) 332.
[60] T. Jiang, X. Zhao, Z. Chen, Y. You, T. Lai, and J. Zhao: Materials Today Physics 26 (2022) 100723.も否定される。

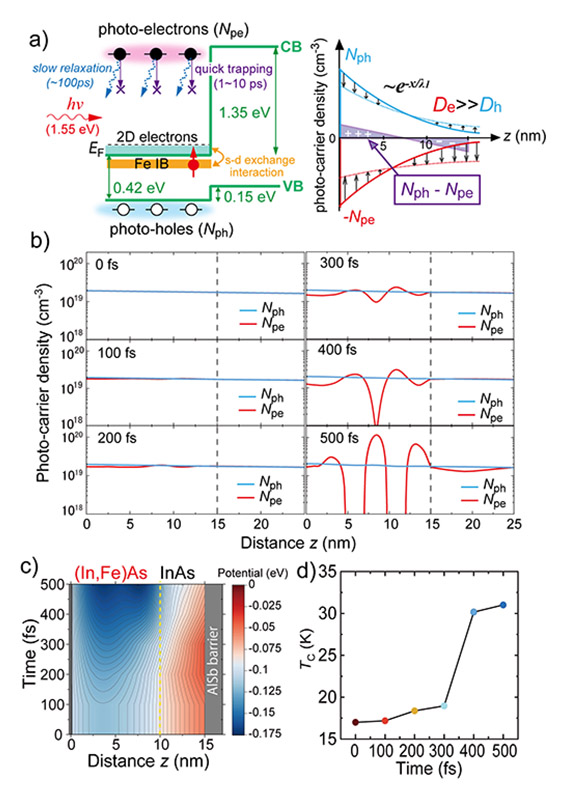
図4　(a) (In,Fe)As/InAs量子井戸にポンプ光が照射される時に生成される光キャリア（正孔、電子、左図）とその分布の時間変化（右図）の概要。(b) 自己無撞着計算で再現した(In,Fe)As/InAs量子井戸の光キャリア分布の時間変化。100 fsごとのタイムステップで計算した。光照射により生成された電子の局所濃度N_pe(z,t)はすぐにAlSb側に拡散するが、光照射により生成された正孔の局所濃度N_ph(z,t)は計算した時間内ではほとんど変化しないため、光デンバー電場が形成される。(c) 量子井戸ポテンシャルが(In,Fe)As層の中心で深くなり、2次元電子キャリアの濃度N_2D(z,t)の再分布を引き起こす。(d) 量子井戸のT_C（青丸）の時間変化を計算した結果。図は文献[63]より改変転載

　しかし、成長軸（z軸）に沿った光キャリアの時間依存の分布により、(In,Fe)As/InAs量子井戸のポテンシャルと2D電子の波動関数が変化し、その磁気特性が変化する可能性がある。ポンプレーザパルスが照射されると、光照射により電子と正孔（光電子、光正孔）が即座に生成され（～1 fs）、光照射直後では表面から基板側に向かって指数関数的に減少する分布を持つ（図4(a)の右パネルを参照）。このとき、光電子N_pe(z)と光正孔N_ph(z)の局所密度は等しいため全体的に光キャリアによる空間電荷が形成されない。次に、z軸に沿った密度勾配により、これらの光キャリアは基板側に向かって拡散し始める。ただし、光電子は、InAs内での移動度が高く、ポンプレーザによって励起される温度が高いため、光正孔よりも速く拡散する。その結果、表面にはより多くの光正孔が、基板側にはより多くの光電子が再分布することによって表面から基板側に向かう電界が時間の経過とともに急速に形成される。これは、いわゆるフォトデンバー電場^[61][61] H. Dember: Phys. Z 32 (1931) 554.であり、InAs^{[61, 62]}[61] H. Dember: Phys. Z 32 (1931) 554.
[62] P. Gu and M. Tani: Terahertz Optoelectronics, edited by K. Sakai (Springer, Berlin) (2005) Chap. 4 63.などの高移動度半導体でテラヘルツ電磁波を生成するために利用されている。(In,Fe)As/InAs量子井戸では、このフォトデンバー電場が上部の(In,Fe)As層に向かって2D電子波動関数を押し、波動関数と(In,Fe)As層の重なりが大きくなるため、これが量子井戸の磁化の強化につながると考えられる。
　上記のシナリオを確認するために、(In,Fe)As/InAs量子井戸内の光キャリアと2D電子の時間依存分布の数値計算を行った（詳しい計算方法は論文^[63][63] L. D. Anh, M. Kobayashi: T. Takeda, K. Araki, R. Okano et al.: Adv. Mater. 35 (2023) 2301347.を参照されたい）。(In,Fe)As/InAs量子井戸中には大量のFeが添加されているため、(In,Fe)Asの電子移動度はInAsより低く、通常100 cm²/Vs程度である^[46][46] P. N. Hai, L. D. Anh, S. Mohan, T. Tamegai, M. Kodzuka et al.: Appl. Phys. Lett. 101 (2012) 182403.。したがって、光キャリアの散乱の性質により、光キャリアの移動度μが低いと仮定するのが現実的である。我々は光電子（μ_e = 2 cm²/Vs）と光正孔（μ_h = 0.2 cm²/Vs）の移動度は低いと仮定して、ポンプレーザパルスに対する(In,Fe)As/InAs量子井戸のポテンシャルと2D波動関数、および光キャリアの空間分布の100 fsのタイムステップごとの応答を計算した。図4(b)に示すように、光電子はすぐにAlSb側に拡散するが、(In,Fe)As/InAs界面およびInAs/AlSb界面での反射により局所濃度N_pe(z,t)が強く振動している。一方、光正孔の局所濃度N_ph(z,t)は計算した時間内ではほとんど変化しない。その結果、時間の経過とともに、光電子と光正孔の局所濃度の差が急速に発生するために、(In,Fe)As/InAs量子井戸ポテンシャルは(In,Fe)As層の中心で深くなり（図4(c)を参照）、2次元電子キャリアの濃度N_2D(z,t)の再分布を引き起こす。この変化により(In,Fe)As領域の局所的な2D電子キャリア濃度が増加し、これがキュリー温度の上昇の原因となったと考えられる。2D電子波動関数を用いて、(In,Fe)As/InAs量子井戸のT_Cは次式で与えられる^[49-51][49] L. D. Anh, P. N. Hai and M. Tanaka: Appl. Phys. Lett. 104 (2014) 042404.
[50] L. D. Anh, P. N. Hai, Y. Kasahara, Y. Iwasa and M. Tanaka: Phys. Rev. B 92 (2015) 161201(R).
[51] B. Lee, T. Jungwirth, and A. H. MacDonald: Phys. Rev. B 61 (2000) 15606.。

式（1）

ここで、SはFe原子のスピン角運動量（= 5/2）、J_sdはs-d交換相互作用定数、A_F^2D = 1.2は2次元構造におけるストーナー補正係数^[64][64] T. Dietl, A. Haury and Y. Merle d'Aubigne: Phys. Rev. B 55 (1997) R3347.、k_BはBoltzmann係数、m^*は電子の有効質量、N_FeはFe原子密度φ_j(z)、は占有量子化準位E_jの波動関数である。式（1）の唯一のフィッティングパラメーターはJ_sdであり、これはs-d交換相互作用エネルギーで決まる。図4(d)に示すように、0.054 eV・nm^-3という妥当なJ_sd（1 eVのs-d交換相互作用エネルギーN₀αに相当）^[48-50][48] L. D. Anh, P. N. Hai and M. Tanaka: Nature Commun. 7 (2016) 13810.
[49] L. D. Anh, P. N. Hai and M. Tanaka: Appl. Phys. Lett. 104 (2014) 042404.
[50] L. D. Anh, P. N. Hai, Y. Kasahara, Y. Iwasa and M. Tanaka: Phys. Rev. B 92 (2015) 161201(R).を使用すると、(In,Fe)As/InAs量子井戸の可視光MCDの温度依存性から見積もられたT_Cが定量的に再現された。特に電子が占有する量子化準位の数が400 fsで1から2に増加したときにT_Cが急増する。この結果は、全体的な電子波動関数の変化により、T_Cが17 Kから31 Kへ増加することを明確に示している。これは、光キャリアの移動度が低い（0.2～2 Vs/cm²）と仮定しても、光ポンピングの最初の500 fsで発生する磁化の増大が再現されたことを意味する。したがって、ここで我々が提案した波動関数の操作によって磁化が変化したというモデルにより、(In,Fe)As/InAs量子井戸において観測されたサブpsという超高速での磁化の増大を説明できたといえる。

4. 結論と展望
　磁性材料の磁化をサブpsの超高速時間スケールで制御できることは、強磁性半導体量子井戸の顕著な特長である。(In,Fe)As/InAsから成る量子井戸中の2Dキャリア分布（波動関数）と強磁性半導体(In,Fe)As層との重なりを変えることにより超高速磁化制御が可能であることを、fsレーザ光を用いたポンプ・プローブ法により実証した。キャリアの波動関数を制御する方法は本研究で行った光ポンピングに限定されるものではなく、トランジスタ構造においてゲート電圧を印加することによって実行することもできる。この波動関数工学では、強磁性量子井戸中にキャリア濃度の変化を起こす必要がないため、材料とデバイスを適切に設計することでゲート容量Cを可能な限り低減できる。したがって、CR定数（Rは配線抵抗）によって制限されるゲート動作速度はサブpsにまで速くすることができる。本研究で実験的に示したように、スピン－キャリア相互作用による磁化制御時間は1 psより短いため、波動関数制御法を利用した強磁性の電気的制御は半導体エレクトロニクスと整合性があり、将来的には超高速でスケーラブルなスピントロニクスデバイスに応用できる可能性がある。

謝辞
　本研究の実施に当たってご協力・議論いただいた松田巌、堀尾眞史、鷲見寿秀、山本航平、武田崇仁、荒木恒星、岡野諒、久保田雄也、矢橋牧名、大和田成起の各氏に感謝する。この研究の一部は、科学研究費補助金（19K21961、20H05650、23K17324）、科学技術振興機構CREST（JPMJCR1777）およびPRESTO（JPMJPR19LB）、UTEC-東京大学FSI研究助成プログラム、村田科学財団、およびスピントロニクス学術研究基盤と連携ネットワーク（Spin-RNJ）の支援を受けた。XFEL実験は、高輝度光科学研究センター（JASRI）の承認を得て、SACLAのBL1で実施された（提案番号2018A8064、2018B8022、2019A8001、2019B8060、2020A8063）。

参考文献
[1] I. Žutić, J. Fabian, and S. Das Sarma: Rev. Mod. Phys. 76 (2004) 323-410.
[2] K. A. Mistry: 2007 IEEE Intl. Electron Devices Meeting. (2007) 247-250.
[3] A. Kirilyuk, A. V. Kimel, and T. Rasing: Rev. Mod. Phys. 82 (2010) 2731-2784.
[4] E. Beaurepaire, J. -C. Merle, A. Daunois and J. -Y. Bigot: Phys. Rev. Lett. 76 (1996) 4250.
[5] J. Hohlfeld, E. Matthias, R. Knorren and K. H. Bennemann: Phys. Rev. Lett. 78 (1997) 4861.
[6] A. Scholl, L. Baumgarten, R. Jacquemin and W. Eberhardt: Phys. Rev. Lett. 79 (1997) 5146.
[7] B. Koopmans, M. van Kampen, J. T. Kohlhepp, and W. J. M. de Jonge: Phys. Rev. Lett. 85 (2000) 844.
[8] H.-S. Rhie, H. A. Dürr, and W. Eberhardt: Phys. Rev. Lett. 90 (2003) 247201.
[9] M. Lisowski, P. A. Loukakos, A. Melnikov, I. Radu, L. Ungureanu et al.: Phys. Rev. Lett. 95 (2005) 137402.
[10] M. Cinchetti, M. Sanchez Albaneda, D. Hoffmann, T. Roth, J. P. Wustenberg et al.: Phys. Rev. Lett. 97 (2006) 177201.
[11] C. Stamm, T. Kachel, N. Pontius, R. Mitzner, T. Quast et al.: Nature Mater. 6 (2007) 740.
[12] E. Carpene, E. Mancini, C. Dallera, M. Brenna, E. Puppin et al.: Phys. Rev. B 78 (2008) 174422.
[13] E. A. Mashkovich, K.A. Grishunin, H. Munekata, & A.V. Kimel: Appl. Phys. Lett. 117 (2020) 122406.
[14] G. Ju, A. V. Nurmikko, R. F. Farrow, R. F. Marks, M. J. Carey et al.: Phys. Rev. B 58 (1998) R11857.
[15] L. H. F. Andrade, A. Laraoui, M. Vomir, D. Muller, J.-P. Stoquert et al.: Phys. Rev. Lett. 97 (2006) 127401.
[16] D. M. Wang, Y. H. Ren, X. Liu, J. K. Furdyna, M. Grimsditch et al.: Phys. Rev. B 75 (2007) 233308.
[17] Y. Hashimoto, S. Kobayashi and H. Munekata: Phys. Rev. Lett. 100 (2008) 067202.
[18] E. Rozkotová, P. Němec, P. Horodyská, D. Sprinzl, F. Trojánek et al.: Appl. Phys. Lett. 92 (2008) 122507.
[19] J. Qi, Y. Xu, A. Steigerwald, X. Liu, J. K. Furdyna et al.: Phys. Rev. B 79 (2009) 085304.
[20] Y. Yang, R. B. Wilson, J. Gorchon, C. –H. Lambert, S. Salahuddin et al.: Sci. Adv. 3 (2017) e1603117.
[21] C. D. Stanciu, F. Hansteen, A. V. Kimel, A. Kirilyuk, A. Tsukamoto et al.: Phys. Rev. Lett. 99 (2007) 047601.
[22] S. Mangin, M. Gottwald, C-H. Lambert, D. Steil, V. Uhlíř et al.: Nat. Mater. 13 (2014) 286-292.
[23] C-H. Lambert, S. Mangin , B. S. D. Ch. S. Varaprasad, Y. K. Takahashi, M. Hehn et al.: Science 345 (2014) 1337-1340.
[24] C. Banerjee, N. Teichert, K. E. Siewierska, Z. Gercsi, G. Y. P. Atcheson et al.: Nat. Commun. 11 (2020) 1-6.
[25] I. Radu, K. Vahaplar, C. Stamm, T. Kachel, N. Pontius et al.: Nature 472 (2011) 205-208.
[26] T. A. Ostler, J. Barker, R.F.L. Evans, R.W. Chantrell, U. Atxitia et al.: Nat. Commun. 3 (2012) 666.
[27] K. Yamamoto, S. El Moussaoui, Y. Hirata, S. Yamamoto, Y. Kubota et al.: Appl. Phys. Lett. 116 (2020) 172406.
[28] J. Wang, I. Cotoros, K. M. Dani, X. Liu, J. K. Furdyna, and D. S. Chemla: Phys. Rev. Lett. 98 (2007) 217401.
[29] F. Liu, T. Makino, T. Yamasaki, K. Ueno, A. Tsukazaki et al.: Phys. Rev. Lett. 108 (2012) 257401.
[30] D. Rudolf, C. La-O-Vorakiat, M. Battiato, R. Adam, J. M. Shaw et al.: Nature Commun. 3 (2012) 1037.
[31] P. Elliott, T. Müller, J. K. Dewhurst, S. Sharma and E. K. U. Gross: Sci. Rep. 6 (2016) 38911.
[32] F. Siegrist, J. A. Gessner, M. Ossiander, C. Denker, Y.-P. Chang et al.: Nature 571 (2019) 240-244.
[33] P. Tengdin, C. Gentry, A. Blonsky, D. Zusin, M. Gerrity et al.: Sci. Adv. 6 (2020) eaaz1100.
[34] M. Hofherr, S. Häuser, J. K. Dewhurst, P. Tengdin, S. Sakshath et al.: Sci. Adv. 6 (2020) eaay8717.
[35] D. Steil, J. Walowski, F. Gerhard, T. Kiessling, D. Ebke et al.: Phys. Rev. Research 2 (2020) 023199.
[36] J. U. Thiele, M. Buess and C. H. Back: Appl. Phys. Lett. 85 (2004) 2857-2859.
[37] G. Ju, J. Hohlfeld, B. Bergman, R. J. M. van de Veerdonk, O. N. Mryasov et al.: Phys. Rev. Lett. 93 (2004) 197403.
[38] G. Li, R. Medapalli, J. H. Mentink, R. V. Mikhaylovskiy, T. G. H. Blank et al.:Nature Commun. 13 (2022) 2998.
[39] C. Vicario, C. Ruchert, F. Ardana-Lamas, P. M. Derlet, B. Tudu et al.: Nat. Photonics 7 (2013) 720.
[40] S. Bonetti, M. C. Hoffmann, M.-J. Sher, Z. Chen, S.-H. Yang et al.: Phys. Rev. Lett. 117 (2016) 087205.
[41] T. Kampfrath, K. Tanaka, and K. A. Nelson: Nat. Photonics 7 (2013) 680.
[42] T. Ishii, H. Yamakawa, T. Kanaki, T. Miyamoto, N. Kida et al.: Appl. Phys. Lett. 114 (2019) 062402.
[43] H. Ohno: Science 281 (1998) 951-956.
[44] M. Tanaka, S. Ohya, and P. N. Hai: Appl. Phys. Rev. 1 (2014) 011102.
[45] T. Dietl, H. Ohno, F. Matsukura, J. Cibert and D. Ferrand: Science 287 (2000) 1019-1022.
[46] P. N. Hai, L. D. Anh, S. Mohan, T. Tamegai, M. Kodzuka et al.: Appl. Phys. Lett. 101 (2012) 182403.
[47] P. N. Hai, L. D. Anh and M. Tanaka: Appl. Phys. Lett. 101 (2012) 252410.
[48] L. D. Anh, P. N. Hai and M. Tanaka: Nature Commun. 7 (2016) 13810.
[49] L. D. Anh, P. N. Hai and M. Tanaka: Appl. Phys. Lett. 104 (2014) 042404.
[50] L. D. Anh, P. N. Hai, Y. Kasahara, Y. Iwasa and M. Tanaka: Phys. Rev. B 92 (2015) 161201(R).
[51] B. Lee, T. Jungwirth, and A. H. MacDonald: Phys. Rev. B 61 (2000) 15606.
[52] T. Ishikawa et al.: Nat. Photonics 6 (2012) 540.
[53] S. Owada, K. Togawa, T. Inagaki, T. Hara, T. Tanaka et al.: J. Synchrotron Radiat. 25 (2018) 282.
[54] Sh. Yamamoto, M. Taguchi, M. Fujisawa, R. Hobara, S. Yamamoto et al.: Phys. Rev. B 89 (2014) 064423.
[55] M. Kobayashi, L. D. Anh, J. Minár, W. Khan, S. Borek et al.: Phys. Rev. B 103 (2021) 115111.
[56] A. Melnikov, I. Razdolski, T. O. Wehling, E. Th. Papaioannou, V. Roddatis et al.: Phys. Rev. Lett. 107 (2011) 076601.
[57] N. Bergeard, M. Hehn, S. Mangin, G. Lengaigne, F. Montaigne et al.: Phys. Rev. Lett. 117 (2016) 147203.
[58] M. Hofherr, P. Maldonado, O. Schmitt, M. Berritta, U. Bierbrauer et al.: Phys. Rev. B 96 (2017) 100403.
[59] A. Eschenlohr, M. Battiato, P. Maldonado, N. Pontius et al.: Nat. Mater. 12 (2013) 332.
[60] T. Jiang, X. Zhao, Z. Chen, Y. You, T. Lai, and J. Zhao: Materials Today Physics 26 (2022) 100723.
[61] H. Dember: Phys. Z 32 (1931) 554.
[62] P. Gu and M. Tani: Terahertz Optoelectronics, edited by K. Sakai (Springer, Berlin) (2005) Chap. 4 63.
[63] L. D. Anh, M. Kobayashi: T. Takeda, K. Araki, R. Okano et al.: Adv. Mater. 35 (2023) 2301347.
[64] T. Dietl, A. Haury and Y. Merle d'Aubigne: Phys. Rev. B 55 (1997) R3347.

レ　デゥック　アイン　Le Duc ANH
東京大学
工学系研究科　電気系工学専攻
スピントロニクス学術連携研究教育センター
〒113-8658　東京都文京区本郷7-3-1
TEL : 03-5841-6654
e-mail : anh@cryst.t.u-tokyo.ac.jp

小林　正起　KOBAYASHI Masaki
東京大学
工学系研究科　電気系工学専攻
スピントロニクス学術連携研究教育センター
〒113-8658　東京都文京区本郷7-3-1
TEL : 03-5841-6692
e-mail : masaki.kobayashi@ee.t.u-tokyo.ac.jp

田中　雅明　TANAKA Masaaki
東京大学
工学系研究科　電気系工学専攻
スピントロニクス学術連携研究教育センター
〒113-8658　東京都文京区本郷7-3-1
TEL : 03-5841-6728
e-mail : masaaki@ee.t.u-tokyo.ac.jp