Volume 28, No.4 Pages 349 - 354

1. はじめに
　物質の性質は原子を構成する電子の状態によって支配されている。X線は物質中の電子と相互作用し、その電子状態を調べることができるため、物質科学の研究において不可欠なツールである。X線を用いる数多くの実験手法の中でX線回折は最も有名で様々な分野の研究者に利用されている手法の一つである。分析手法として広く認知されているX線回折法は、その簡便さから、物理学・化学・生命科学・材料科学などの様々な分野で重宝されている。X線回折は原子の持つ電子の散乱現象に基づいており、結晶内の原子の種類とその配列状態（結晶構造）を同定することができる。結晶構造解析では、実験で得られるX線回折強度を基に、仮定した構造モデルの原子座標や原子変位パラメータ（通称、温度因子）などを最小二乗法によって精密化する。最近では、実験室系の単結晶X線回折装置の発展は目覚ましく、良質な単結晶さえ準備すれば、測定や構造解析のほとんどが自動化されており、（X線回折の原理を知らなくても、）実験終了と同時に結晶構造の情報を得ることができる。
　では、X線回折実験において、放射光を利用するメリットはなんであろうか？1つ目のメリットは強度である。放射光の非常に明るい光を用いることで、実験室で使用される特性X線とは桁違いに強い回折強度を得ることができる。これによって、結晶中の微小な構造変化、短距離秩序、元素欠損、元素置換などを高精度に決定することができる。
　2つ目のメリットは高いエネルギーである。実験室系では、Agの特性X線を用いたとしても、そのエネルギーは22keV程度である。一方、大型放射光施設SPring-8の単結晶X線回折用ビームライン（BL02B1）では60keV程度の高エネルギーX線を利用することができる。ブラッグの法則（nλ = 2d sinθ）から分かるように、高エネルギー（短波長λ）のX線を用いることで、面間隔dが小さい回折強度の情報を得ることができる。ただし、通常の構造解析において、高エネルギーX線を用いることで得られる恩恵はそれほど多くない。もちろん、より多くの回折ピークの強度情報が得られるため、解析における構造パラメータの収束度や信頼度は向上するものの、解析結果が劇的に変化することはない。では、放射光は実験室系に比べて単に定量性の高い実験や解析ができるだけであろうか？この疑問に対して、本稿ではSPring-8の高強度・高エネルギーX線を最大限に活かした価電子密度観測手法について紹介する。この手法を用いることで初めて得られた、実験室系の単結晶X線回折とは質的に異なる最近の研究成果について、いくつかの物質を例に挙げて紹介する。

2. コア差フーリエ合成法による価電子密度観測手法の提案
　電子軌道とは実空間における電子の存在確率に対応し、物性を規定する最小単位である。原子核周りの電子の中でも、物性に寄与するのは最外殻の軌道を占有する価電子である。従って、価電子密度分布の実空間観測は物性を理解するために非常に有効な手段である。
　X線回折で得られる強度は結晶中の全電子密度のフーリエ変換に対応する。従って、原理的には無限の回折ピークの強度を逆フーリエ変換することで、電子密度分布を観測できるはずである。しかし、実験では有限の回折ピークの情報しか得ることはできない。具体的には、観測可能な面間隔dの最小値d_min（Å）はd_min = λ/(2 sinθ_max) ≅ 6.2/(E sinθ_max)となり、使用するX線のエネルギーE（keV）と散乱角の最大値θ_maxに依存する。このとき、d_minは電子密度を描画する際の実空間分解能（きめ細かさ）に対応する。図1(a)、(b)にSPring-8のX線回折データ（d_min = 0.25 Å）をもとに、通常の逆フーリエ変換によって得られた、ダイヤモンド単結晶の全電子密度分布を示す^[1][1] S. Kitou, Y. Hosogi, R. Kitaura, T. Naito, T. Nakamura, and H. Sawa: Crystals 10 (2020) 998.。原子周りにおいて電子密度分布は大きく乱れており、C-C間に存在するはずの共有結合を正しく捉えられないことが分かる。これは実験で得られる回折ピークの強度が有限なことに起因する、フーリエ合成の数学的な打ち切りの影響である。つまり、良質な単結晶試料と高エネルギーX線を用いたとしても、電子密度分布を精密に観測することはできない。

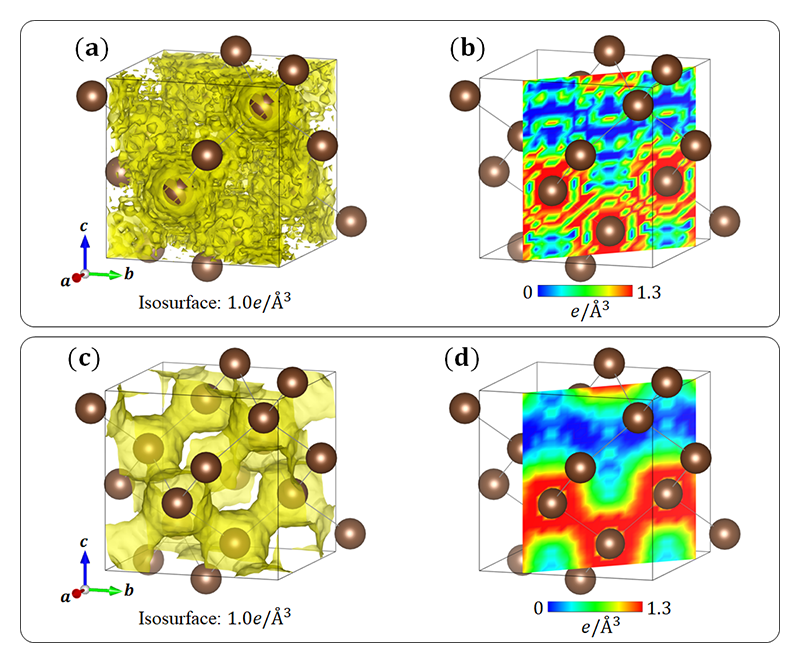
図1　(a)、(b) 通常の逆フーリエ変換によって得られたダイヤモンドの全電子密度分布。(c)、(d) コア差フーリエ合成（CDFS）法によって得られたダイヤモンドの価電子密度分布。文献[1]より引用。

　これに対して、我々のグループでは単結晶中の価電子の情報のみを効率的に抽出する方法として、コア差フーリエ合成（core differential Fourier synthesis; CDFS）法を提案した^{[2, 3]}[2] S. Kitou, T. Fujii, T. Kawamoto, N. Katayama, S. Maki, E. Nishibori, K. Sugimoto, M. Takata, T. Nakamura, and H. Sawa: Phys. Rev. Lett. 119 (2017) 065701.
[3] S. Kitou, T. Manjo, N. Katayama, T. Shishidou, T. Arima, Y. Taguchi, Y. Tokura, T. Nakamura, T. Yokoyama, K. Sugimoto, and H. Sawa: Phys. Rev. Research. 2 (2020) 033503.。本手法については文献［4、5］の解説記事で詳細に説明されているので、ご興味がある方はそちらを参照されたい。ここでは、簡単にこの手法のコンセプトを紹介する。図2にCDFS法の概略図を示す。X線回折実験で得られる全電子密度の情報から、球対称な内殻電子の寄与をモデル的に差し引くことで、価電子密度の情報のみを抽出する。

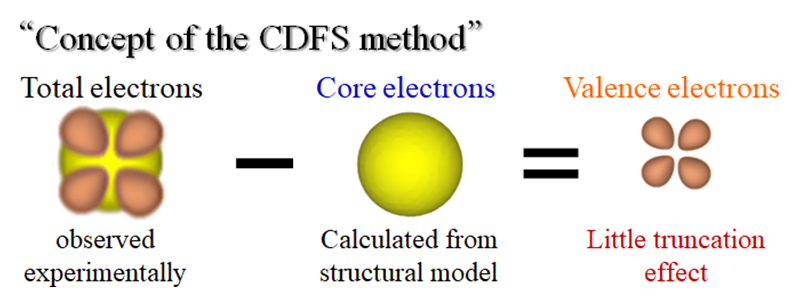
図2　CDFS法による価電子密度観測の概略図。

　ここで、原子散乱因子に立ち返る。図3に例として炭素Cの原子散乱因子を示す^[6][6] Z. Su, and P. Coppens: Acta Cryst. A53 (1997) 749.。全電子（内殻電子 + 価電子）、内殻電子、価電子の寄与をそれぞれ黒色、青色、橙色で示す。内殻電子は散乱角の大きな領域まで有限の値を持つのに対して、価電子はsinθ/λ = 0.5 Å^-1程度までしか値を持たない。この振る舞いは、それぞれの電子の空間分布状態を反映している。X線回折実験の場合、測定可能な範囲はsinθ/λ < 2 Å^-1程度であり、範囲外の回折強度の情報は得られない。このとき、実験的に観測できない高角領域（sinθ/λ > 2 Å^-1）において、内殻電子に由来する有限の値が逆フーリエ変換に組み込めないため、数学的な打ち切りの影響が顕著に現れる。一方、これに対してCDFS法で抽出される価電子の寄与は、高角領域においてほとんど値を持たないため、打ち切りの影響を極力抑えることができる。実際に、図1(c)、(d)にCDFS解析で得られたダイヤモンドの価電子密度分布を示す^[1][1] S. Kitou, Y. Hosogi, R. Kitaura, T. Naito, T. Nakamura, and H. Sawa: Crystals 10 (2020) 998.。C-C間にsp³軌道混成に対応する結合電子がはっきりと存在することが分かる。ただし、ダイヤモンドの原子間に存在する結合電子は波長の長い波として表現できるため、実はそれほど高い空間分解能（高エネルギーのX線）でなくとも観測は可能である。

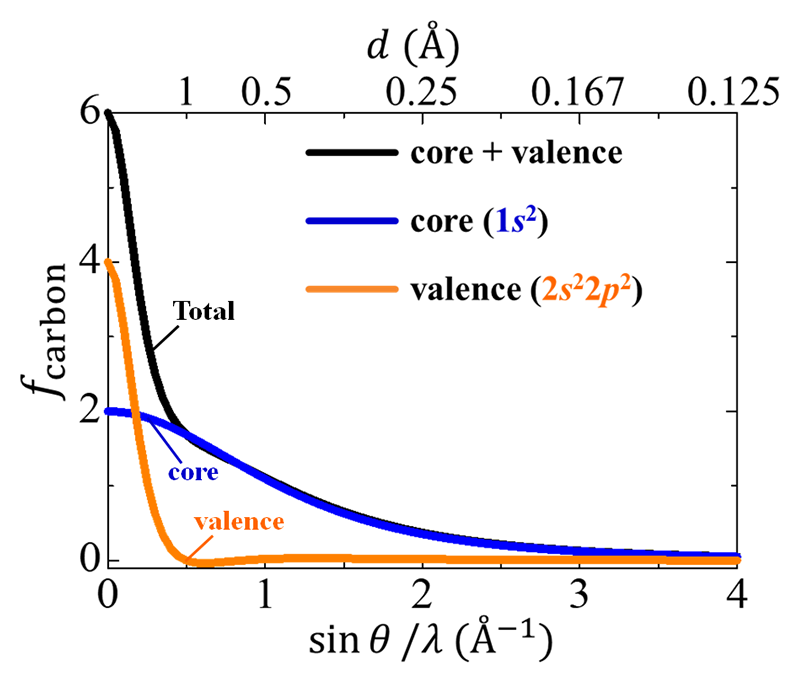
図3　炭素Cの原子散乱因子^[6][6] Z. Su, and P. Coppens: Acta Cryst. A53 (1997) 749.。

3. 遷移金属酸化物におけるd電子の観測
3.1 d電子密度分布の観測に関する考察
　多くの遷移金属酸化物では、伝導性や磁性を担うのはd軌道を占有する価電子である。この原子サイト上に局在するd電子の観測には高エネルギーX線が不可欠となる。ここで、X線回折データの分解能と電子密度分布の関係について、簡単な計算を行う。図4(a)に計算によって得られたTiの3d_xy軌道の電子密度分布ρ(r)を示す。得られたρ(r)をフーリエ変換することで、構造因子F(K)が得られる。ここで、F(K)をもう一度逆フーリエ変換する。このとき、計算に使用する散乱ベクトルKの範囲をd_min = 2π/|K_max|の値によって制限することで、実験的な分解能d_minを考慮した電子密度分布ρ_tra(r)が得られる（図4(b)、(c)）。Tiの3d_xy電子の場合は、d_min = 0.25 Åで計算したρ_tra(r)はρ(r)とほぼ一致している。一方、d_minが大きくなるほど、電子密度がぼやけていき3d_xy電子の異方性が正しく捉えられないことが分かる。従って、3d電子を正確に観測するにはd_min = 0.25 Å程度のX線回折データが不可欠である。また、ここまでの考察から、注目する軌道の動径方向の分布から実験に必要な空間分解能をある程度予想できることが分かる。以下では、高エネルギーX線（d_min ≅ 0.25 ÅのX線回折データ）を用いることで得られた、d電子の観測例について紹介する。

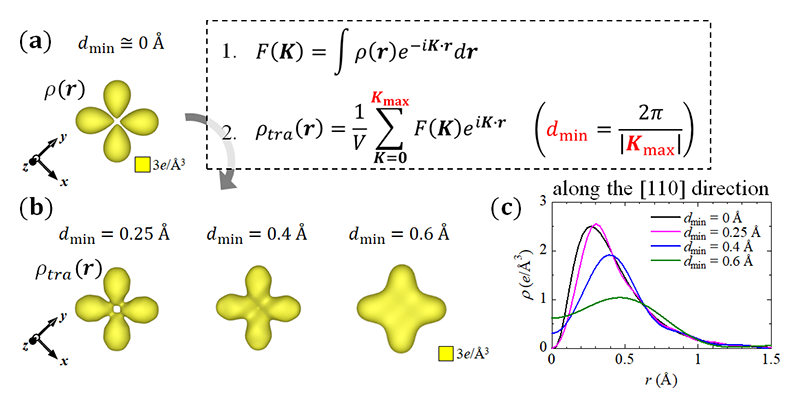
図4　(a) Tiの3d_xy軌道の電子密度分布ρ(r)。(b) 有限のフーリエ級数F(K)を用いて計算した3d_xy電子密度分布ρ_tra(r)。(c) [110]方向に沿った3d_xy電子密度分布の1次元プロットのd_min依存性。

3.2 YTiO₃におけるTi³⁺ 3d¹電子
　CDFS解析を用いたd軌道観測の最初の対象物質として、1970年代から現在に至るまで軌道観測実験の標準的な物質として多角的に調べられているペロブスカイト型酸化物YTiO₃に着目した（図5(a)）。モット絶縁体であるYTiO₃において、物性を担うTi³⁺イオンは19個の電子を持っているが、その内18個の内殻電子は全体で等方的な分布状態を形成し、物性にはほとんど寄与しない。この系の電子状態を支配するのはTiの3d軌道を占有するたった1個の価電子であり、過去の実験や理論計算からは図5(b)のような軌道状態と蝶々型の価電子密度分布が予想されている^[7-12][7] T. Mizokawa, and A. Fujimori: Phys. Rev. B 54 (1996) 5368.
[8] H. Sawada, N. Hamada, and K. Terakura: Physica B 237 (1997) 46.
[9] M. Itoh, M. Tsuchiya, H. Tanaka, and K. Motoya: J. Phys. Soc. Jpn. 68 (1999) 2783.
[10] J. Akimitsu, H. Ichikawa, N. Eguchi, T. Miyano, M. Nishi, and K. Kakurai: J. Phys. Soc. Jpn. 70 (2001) 3475.
[11] H. Nakao, Y. Wakabayashi, T. Kiyama, Y. Murakami, M. V. Zimmermann, J. P. Hill, D. Gibbs, S. Ishihara, Y. Taguchi, and Y. Tokura: Phys. Rev. B 66 (2002) 184419.
[12] M. Kubota, H. Nakao, Y. Murakami, Y. Taguchi, M. Iwama, and Y. Tokura: Phys. Rev. B 70 (2004) 245125.。図5(c)にCDFS解析によって得られたTi周りの価電子密度分布を示す^[3][3] S. Kitou, T. Manjo, N. Katayama, T. Shishidou, T. Arima, Y. Taguchi, Y. Tokura, T. Nakamura, T. Yokoyama, K. Sugimoto, and H. Sawa: Phys. Rev. Research. 2 (2020) 033503.。TiO₆八面体の中心に局在しているTiの価電子密度分布は、まさに量子力学の教科書に載っているような蝶々型の3d軌道の形状を反映していることが分かる。さらに、得られた価電密度分布の異方性から、3d軌道秩序状態における波動関数0.79|yz〉 + 0.61|zx〉 - 0.08|xy〉の決定に成功した。この値は、先行研究の実験や理論計算の結果とも整合している^[7-12][7] T. Mizokawa, and A. Fujimori: Phys. Rev. B 54 (1996) 5368.
[8] H. Sawada, N. Hamada, and K. Terakura: Physica B 237 (1997) 46.
[9] M. Itoh, M. Tsuchiya, H. Tanaka, and K. Motoya: J. Phys. Soc. Jpn. 68 (1999) 2783.
[10] J. Akimitsu, H. Ichikawa, N. Eguchi, T. Miyano, M. Nishi, and K. Kakurai: J. Phys. Soc. Jpn. 70 (2001) 3475.
[11] H. Nakao, Y. Wakabayashi, T. Kiyama, Y. Murakami, M. V. Zimmermann, J. P. Hill, D. Gibbs, S. Ishihara, Y. Taguchi, and Y. Tokura: Phys. Rev. B 66 (2002) 184419.
[12] M. Kubota, H. Nakao, Y. Murakami, Y. Taguchi, M. Iwama, and Y. Tokura: Phys. Rev. B 70 (2004) 245125.。このように、量子力学的なモデルを一切仮定せずに、3d価電子密度分布の直接観測に成功した。

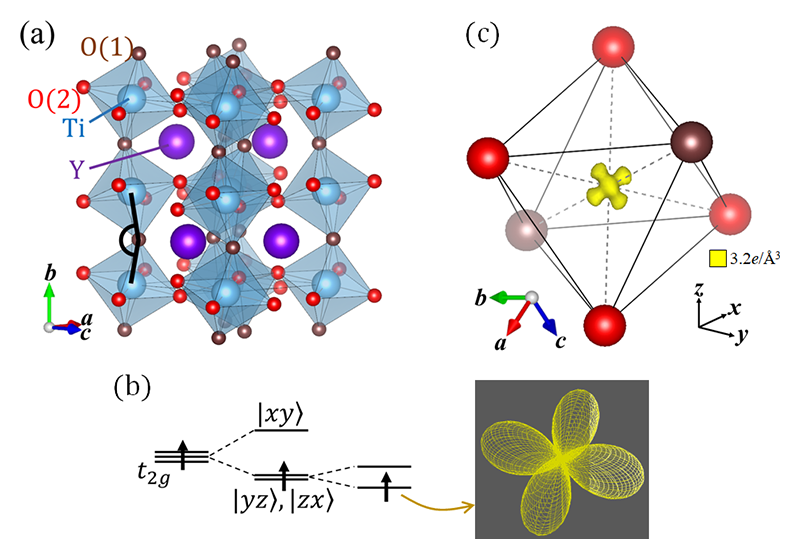
図5　(a) YTiO₃の結晶構造。(b) の軌道状態と予想される電子密度分布。(c) CDFS解析で得られたTiサイト周りの価電子密度分布。文献[3]より引用。

3.3 Nd₂Mo₂O₇におけるMo⁴⁺ 4d²電子
　主量子数n = 3の3d軌道と比べてn = 4の4d軌道は、波動関数の球面調和関数項（角度依存性）は同じであるが、動径方向において節が1つ存在する（図6）。電子密度としては4d軌道には図6(b)のようなdip構造が現れるはずである。しかし、これまで電子密度におけるdip構造を実験的に観測した例はない。我々はSPring-8の高エネルギーX線を用いること4d電子密度の観測を試みた。

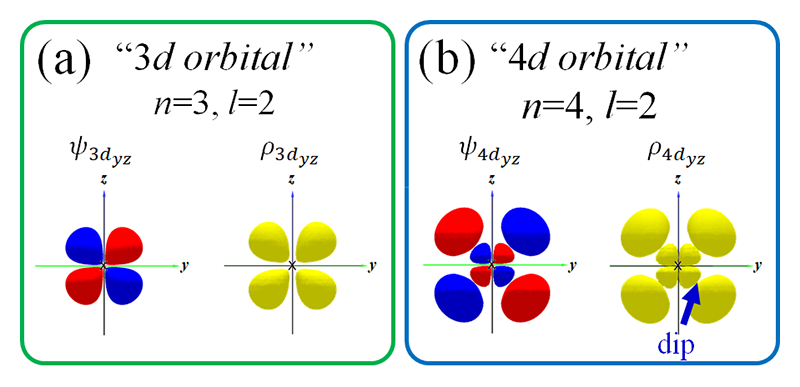
図6　(a) 3d軌道と(b) 4d軌道の波動関数と電子密度の概略図。

　4d軌道観測の対象物質として、パイロクロア型酸化物Nd₂Mo₂O₇に着目した（図7(a)）。この物質は全温度領域において、立方晶空間群Fd3mの高い対称性を有している。Moの形式価数は4+で、4d軌道に2個の電子を占有している。Nd₂Mo₂O₇は金属的な伝導性を示し、約90 Kにおいて強磁性転移を示す^[13][13] N. Ali, M. P. Hill, S. Labroo, and J. E. Greedan: J. Solid State Chem. 83 (1989) 178.。さらに、より低温ではMoの非共面スピン構造に起因して、トポロジカルホール効果を示す^[14][14] Y. Taguchi, Y. Oohara, H. Yoshizawa, N. Nagaosa, and Y. Tokura: Science 291 (2001) 2573.。Moサイトに着目すると、周りの6つの酸素と結合し、八面体を形成している。MoO₆八面体の歪みやこの系の物性から図7(b)のような軌道状態が予想されているが、実験的な観測はなされていない。

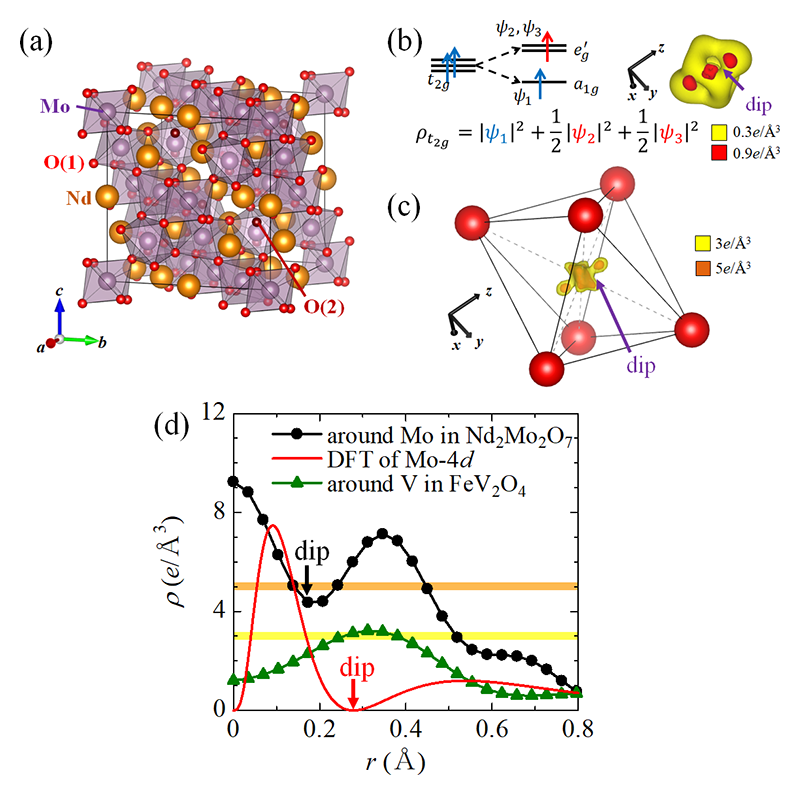
図7　(a) Nd₂Mo₂O₇の結晶構造。(b) の軌道状態と予想される価電子密度分布。(c) CDFS解析で得られたMoサイト周りの価電子密度分布。(d) z軸方向に沿ったMoサイト周りにおける価電子密度の1次元プロット（CDFS解析の結果は黒丸、DFT計算の結果は赤線: 文献[15]より引用）。Vサイト周りにおける価電子密度の1次元プロット（緑三角: 文献[16]より引用）。

　図7(c)にこの系のCDFS解析によって得られたMoサイト周りの価電子密度分布を示す^[15][15] S. Kitou, Y. Kaneko, Y. Nakamura, K. Sugimoto, Y. Nomura, R. Arita, Y. Tokura, H. Sawa, and T. Arima: Phys. Rev. B 108 (2023) 024103.。z方向に伸びるような異方性が観測されており、これは八面体構造から予想される価電子密度の異方性（図7(b)）と一致している。また、この4d軌道状態は二重交換相互作用に起因するこの系における強磁性金属状態^[13][13] N. Ali, M. P. Hill, S. Labroo, and J. E. Greedan: J. Solid State Chem. 83 (1989) 178.と整合する。
　図7(d)にMoサイトの中心からz方向に沿った価電子密度の1次元的プロットを黒色の点で示す^[15][15] S. Kitou, Y. Kaneko, Y. Nakamura, K. Sugimoto, Y. Nomura, R. Arita, Y. Tokura, H. Sawa, and T. Arima: Phys. Rev. B 108 (2023) 024103.。比較として、スピネル型酸化物FeV₂O₄の高温立方晶相におけるVサイト周りの3d価電子密度分布の1次元プロットを緑色の三角で示す^[16][16] T. Manjo, S. Kitou, N. Katayama, S. Nakamura, T. Katsufuji, Y. Nii, T. Arima, J. Nasu, T. Hasegawa, K. Sugimoto, D. Ishikawa, and H. Sawa: Mater. Adv. 3 (2022) 3192.。このとき、VサイトはNd₂Mo₂O₇のMoサイトと同じ対称性(.3m)を有しており、Moと同様に2個の価電子がd軌道を占有している。V 3d価電子密分布にはdip構造がないのに対して、Mo 4d価電子密分布のr = 0.2 Å付近には電子密度が凹んだdip構造が現れていることが分かる。さらに、図7(d)に密度汎関数理論（DFT）を用いて孤立原子を仮定した計算で得られた電子密度の1次元プロットを赤線で示す^[15][15] S. Kitou, Y. Kaneko, Y. Nakamura, K. Sugimoto, Y. Nomura, R. Arita, Y. Tokura, H. Sawa, and T. Arima: Phys. Rev. B 108 (2023) 024103.。DFT計算では波動関数の節において電子密度がほぼゼロになっているが、CDFS法で得られた価電子密度は完全にゼロには落ちていない。また、実験で観測されたdipの位置はDFT計算に比べて、約0.1 Å原子核に近い位置に存在する。現状、実験と計算結果の差異の原因は不明であるが、酸素との軌道混成などが原因である可能性がある。我々は波動関数の節も含めて4d軌道状態の決定に成功した。

4. p-d軌道混成によるリガンドホールの観測
　鉄や銅の酸化物ではしばしば異常原子価状態が現れる。例えば、立方晶ペロブスカイト型酸化物SrFeO₃ 図8(a)は、SrとOの形式価数を2+と2-と仮定すると、Feの価数は珍しい4+となり、3d軌道に4つの電子が占有している。この系では、酸素周りの一部の電子がFeの周りに移動することで、酸素周りにおいて電子が不足した部分（リガンドホール）が存在することが知られている^{[17, 18]}[17] M. Abbate, G. Zampieri, J. Okamoto, A. Fujimori, S. Kawasaki, and M. Takano: Phys. Rev. B 65 (2002) 165120.
[18] A. E. Bocquet, A. Fujimori, T. Mizokawa, T. Saitoh, H. Namatame, S. Suga, N. Kimizuka, Y. Takeda, and M. Takano: Phys. Rev. B 45 (1992) 1561.。リガンドホールは銅酸化物における高温超伝導や、鉄酸化物における磁気秩序と密接に関わっていると予想されている。実際、SrFeO₃は全温度-磁場領域において格子は立方晶の対称性を維持しているにも関わらず、らせん構造やヘッジホッグ構造など多彩な磁気秩序状態が現れる^{[19, 20]}[19] S. Ishiwata, M. Tokunaga, Y. Kaneko, D. Okuyama, Y. Tokunaga, S. Wakimoto, K. Kakurai, T. Arima, Y. Taguchi, and Y. Tokura: Phys. Rev. B 84 (2011) 054427.
[20] S. Ishiwata, T. Nakajima, J.-H. Kim, D. S. Inosov, N. Kanazawa, J. S. White, J. L. Gavilano, R. Georgii, K. M. Seemann, G. Brandl, P. Manuel, D. D. Khalyavin, S. Seki, Y. Tokunaga, M. Kinoshita, Y. W. Long, Y. Kaneko, Y. Taguchi, T. Arima, B. Keimer, and Y. Tokura: Phys. Rev. B 101 (2020) 134406.。しかし、これまでリガンドホールの空間的な分布状態を実験的に観測した例はない。我々は、良質なSrFeO₃単結晶を用いたX線回折実験と価電子密度解析を行った。

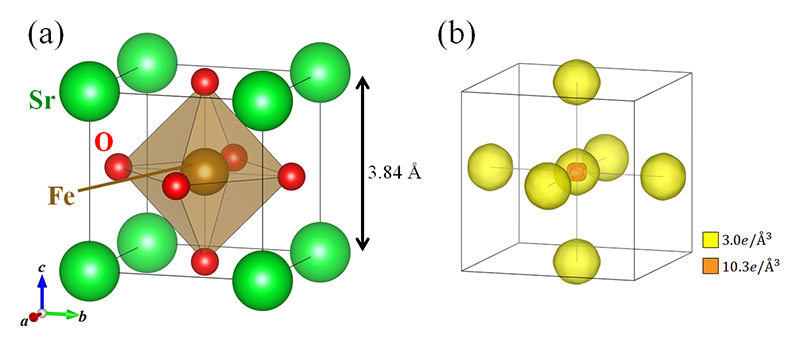
図8　SrFeO₃の(a) 結晶構造と(b) 価電子密度分布。文献[21]より引用。

　図8(b)にCDFS解析によって得られたSrFeO₃の価電子密度分布を示す^[21][21] S. Kitou, M. Gen, Y. Nakamura, K. Sugimoto, Y. Tokunaga, S. Ishiwata, and T. Arima: Adv. Sci. 10 (2023) 2302839.。黄色の等電子面（3 e/ų）を見るとSrサイト周りにおいて電子密度は存在しない。Sr²⁺は最外殻の5s軌道が空となっているため、価電子が存在しないことと整合する。一方、FeとOサイト周りには等方的な黄色で示す電子密度が存在する。さらに、Feサイト周りについてより濃いオレンジ色の等電子面（10.3 e/ų）を見ると、O方向に電子密度が凹んでいることが分かった。
　Fe周りの価電子密度の異方性を精密に議論するために、Feサイトの中心からr = 0.2 Åの距離（電子密度が最も大きいr）に位置する電子密度を球上に表面カラープロットとして表示した（図9(a)）。これは電子密度の球面調和関数項に対応する。図9(c)、(d)にFe⁴⁺ (3d⁴)とFe³⁺ (3d⁵)において予想される電子密度の表面カラープロットを示す。Fe⁴⁺ではO方向に向かって電子密度が薄くなっているのに対し、Fe³⁺では異方性が存在しない。実験で得られたFeサイト周りの異方性から3d電子数を見積もると、4.64(8)となり、Feの価数としては4+と3+の中間状態である3.36(8)+となった。これは、先行研究のX線分光測定の結果と整合している^{[17, 18]}[17] M. Abbate, G. Zampieri, J. Okamoto, A. Fujimori, S. Kawasaki, and M. Takano: Phys. Rev. B 65 (2002) 165120.
[18] A. E. Bocquet, A. Fujimori, T. Mizokawa, T. Saitoh, H. Namatame, S. Suga, N. Kimizuka, Y. Takeda, and M. Takano: Phys. Rev. B 45 (1992) 1561.。また、このことはO周りの電子の一部がFe周りに移動している可能性を示唆する。

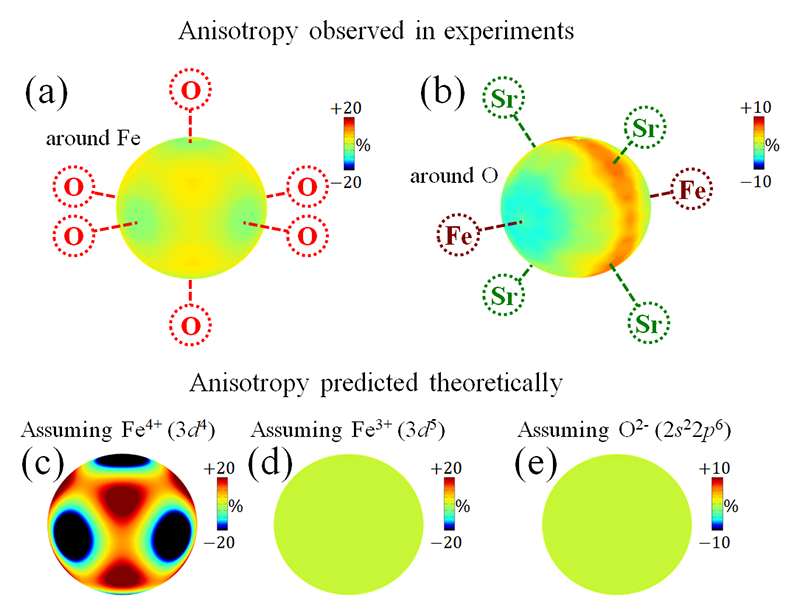
図9　(a) Feサイト周りと(b) Oサイト周りの価電子密度の異方性(球面調和関数項)の表面カラープロット。(c) Fe⁴⁺、(d) Fe³⁺、(e) O^2-を仮定した価電子密度の表面カラープロット。文献[21]より引用。

　理想的なO^2-では図9(e)に示す通り、異方性は存在しない。図9(b)にCDFS解析で得られたO周りの電子密度の球面調和関数項をカラープロットとして示す。
　確かに、Oの電子密度に異方性が存在しており、Fe方向にのみ電子密度が薄くなっている。より詳細な解析の結果、これはFe 3dとO 2pの軌道混成に起因するリガンドホール状態であることが分かった。我々はSrFeO₃の価電子密度分布を高い精度で観測することで、O周りにFe方向に伸びるリガンドホールが存在することを明らかにした。

5. 終わりに
　本稿で紹介したCDFS法による価電子密度観測は非常にシンプルであり、要はSPring-8の高品質なX線回折データから内殻電子の寄与を差し引いた後に逆フーリエ変換を行っているだけである。従って、実験で得られるX線回折強度の質が価電子密度分布の質に直接的に反映される。つまり、測定に用いる「単結晶」、「X線」、「回折計」の質や精度が向上するほど、電子軌道に関するより本質的な情報を抽出することができる。この点については、SPring-8-IIへのアップグレードに伴い、価電子密度観測の精度の大幅な向上が期待できると考えている。また、CDFS法は①原理的には対象物質の示す物性とは独立に全ての元素に適用することができる、②価電子密度分布を抽出する際にいかなる量子力学的・情報学的モデルを仮定する必要がない、③解析者によるバイアスがかかりづらい、という特徴がある。これらの特徴を活かし、今後、CDFS法を用いた価電子密度観測が物質科学の研究に幅広く活用され、その発展に貢献することを期待する。

謝辞
　SPring-8での単結晶X線回折実験は全てBL02B1ビームラインにて、高輝度光科学研究センターの杉本邦久 教授（現 近畿大学）、中村唯我 博士の協力のもと行われた。本研究に関して、名古屋大学の澤博 教授、東京大学の有馬孝尚 教授をはじめとする多くの共同研究者のご協力を頂きました。この場を借りて御礼申し上げます。

参考文献
[1] S. Kitou, Y. Hosogi, R. Kitaura, T. Naito, T. Nakamura, and H. Sawa: Crystals 10 (2020) 998.
[2] S. Kitou, T. Fujii, T. Kawamoto, N. Katayama, S. Maki, E. Nishibori, K. Sugimoto, M. Takata, T. Nakamura, and H. Sawa: Phys. Rev. Lett. 119 (2017) 065701.
[3] S. Kitou, T. Manjo, N. Katayama, T. Shishidou, T. Arima, Y. Taguchi, Y. Tokura, T. Nakamura, T. Yokoyama, K. Sugimoto, and H. Sawa: Phys. Rev. Research. 2 (2020) 033503.
[4] 鬼頭俊介、澤博：日本放射光学会誌「放射光」34 (2021) 64-72.
[5] 澤博、萬條太駿、鬼頭俊介：日本結晶学会誌 64 (2022) 98-106.
[6] Z. Su, and P. Coppens: Acta Cryst. A53 (1997) 749.
[7] T. Mizokawa, and A. Fujimori: Phys. Rev. B 54 (1996) 5368.
[8] H. Sawada, N. Hamada, and K. Terakura: Physica B 237 (1997) 46.
[9] M. Itoh, M. Tsuchiya, H. Tanaka, and K. Motoya: J. Phys. Soc. Jpn. 68 (1999) 2783.
[10] J. Akimitsu, H. Ichikawa, N. Eguchi, T. Miyano, M. Nishi, and K. Kakurai: J. Phys. Soc. Jpn. 70 (2001) 3475.
[11] H. Nakao, Y. Wakabayashi, T. Kiyama, Y. Murakami, M. V. Zimmermann, J. P. Hill, D. Gibbs, S. Ishihara, Y. Taguchi, and Y. Tokura: Phys. Rev. B 66 (2002) 184419.
[12] M. Kubota, H. Nakao, Y. Murakami, Y. Taguchi, M. Iwama, and Y. Tokura: Phys. Rev. B 70 (2004) 245125.
[13] N. Ali, M. P. Hill, S. Labroo, and J. E. Greedan: J. Solid State Chem. 83 (1989) 178.
[14] Y. Taguchi, Y. Oohara, H. Yoshizawa, N. Nagaosa, and Y. Tokura: Science 291 (2001) 2573.
[15] S. Kitou, Y. Kaneko, Y. Nakamura, K. Sugimoto, Y. Nomura, R. Arita, Y. Tokura, H. Sawa, and T. Arima: Phys. Rev. B 108 (2023) 024103.
[16] T. Manjo, S. Kitou, N. Katayama, S. Nakamura, T. Katsufuji, Y. Nii, T. Arima, J. Nasu, T. Hasegawa, K. Sugimoto, D. Ishikawa, and H. Sawa: Mater. Adv. 3 (2022) 3192.
[17] M. Abbate, G. Zampieri, J. Okamoto, A. Fujimori, S. Kawasaki, and M. Takano: Phys. Rev. B 65 (2002) 165120.
[18] A. E. Bocquet, A. Fujimori, T. Mizokawa, T. Saitoh, H. Namatame, S. Suga, N. Kimizuka, Y. Takeda, and M. Takano: Phys. Rev. B 45 (1992) 1561.
[19] S. Ishiwata, M. Tokunaga, Y. Kaneko, D. Okuyama, Y. Tokunaga, S. Wakimoto, K. Kakurai, T. Arima, Y. Taguchi, and Y. Tokura: Phys. Rev. B 84 (2011) 054427.
[20] S. Ishiwata, T. Nakajima, J.-H. Kim, D. S. Inosov, N. Kanazawa, J. S. White, J. L. Gavilano, R. Georgii, K. M. Seemann, G. Brandl, P. Manuel, D. D. Khalyavin, S. Seki, Y. Tokunaga, M. Kinoshita, Y. W. Long, Y. Kaneko, Y. Taguchi, T. Arima, B. Keimer, and Y. Tokura: Phys. Rev. B 101 (2020) 134406.
[21] S. Kitou, M. Gen, Y. Nakamura, K. Sugimoto, Y. Tokunaga, S. Ishiwata, and T. Arima: Adv. Sci. 10 (2023) 2302839.

鬼頭　俊介　KITOU Shunsuke
東京大学　大学院新領域創成科学研究科
〒277-8561　千葉県柏市柏の葉5-1-5
TEL : 04-7136-3769
e-mail : kitou@edu.k.u-tokyo.ac.jp