Volume 27, No.4 Pages 329 - 335
1. 最近の研究から/FROM LATEST RESEARCH
2019年度指定パートナーユーザー活動報告
精密価電子密度解析による軌道物理の研究
Study of Orbital Physics by Precise Density Analysis of Valence Electrons
(1)
| 指定時PU課題番号/ビームライン | 2019A0070/BL02B1 | ||||
| PU氏名(所属) | 澤 博(名古屋大学) | ||||
| 研究テーマ | オペランド計測を含めた精密電子密度解析による軌道物理の研究 | ||||
| 高度化 | オペランド計測を目指した精密電子密度解析の高性能化 | ||||
| 利用研究支援 | 当該装置を用いた利用実験の支援 | ||||
| 利用期 | 19A | 19B | 20A | 21A | 合計 |
| PU課題実施シフト数 | 35.75 | 41.5 | 35.875 | 41.125 | 154.25 |
| 支援課題数 | - | - | - | 1 | 1 |
(2)PU活動概要
1. はじめに
物性を理解することは、その系の電子状態を理解することに他ならない。量子化学計算や第一原理計算が高度化されて様々な物性の舞台である電子状態を表現できるようになってきたが、電子相関が物性を支配するような系では近似法やパラメータなどの選択に流派が存在するために、異なる結果を与えることが論争を巻き起こすこともある。特に、分子動力学法による時間発展や電子励起状態の記述については、まだまだ十分な結果を与えられない。そこで、やはり実験的に電子状態を明らかにすることが望まれる。例えば、光電子分光法は多くの系に適用されて、フェルミエネルギーに近い電子系の分散関係を直接観測できることが、昨今の物質開発において重要な役割を担っている。このように、放射光を用いた分光学的な実験手法の進化には目を見張るものがある。
一方、回折実験については、放射光X線の高輝度化などによって粉末測定の高精度化や対象とする結晶の微小化、より短時間で測定可能なハイスループット化などにその開発方向が偏っている。単結晶のX線回折については、国内で精密解析に取り組んでいる研究者が少ないこともあり、時代に置き去りにされつつあるようである。そのような中、我々は構造物性の観点から「世界に誇る高品質の放射光X線を用いた回折実験はどこまでその電子状態に迫れるか」という問題提起に完全に魅せられて、「超精密解析」と(勝手に)銘打って価電子密度分布解析から量子パラメータを決定できることを提案している。また、軌道の自由度が直接的に物性に寄与するような系の場合、この軌道自由度と物性の関係に注目するのがタイトルにもある「軌道物理」である。このような価電子密度分布の有用性を鑑みて周期的な構造を有する結晶についての回折実験を放射光で行うことに特化し高度化を試みたのが、このPUである。
2. X線回折強度と電子密度分布解析
まず、構造物性の立場から見たとき、ユニットセル内の全電子密度を得られたとしても電子状態の解釈には不十分である。物質の解釈には、少なくとも価電子密度分布の情報が必要である。通常の構造解析では、モデルに含まれない結合電子や軽元素の情報を抽出するために差フーリエ合成を行う。ここではごく簡単に、この差フーリエ合成を発展させた新しい価電子密度分布解析を説明する。この手法を有効に利用するためには、大きく分けて二つの課題、①回折強度のダイナミックレンジとその統計精度、②High-Qの測定を行うことで得られる十分な空間分解能、を解決する必要がある。どちらが欠けても得られる情報の信頼度は甚だしく損なわれるため、放射光X線回折実験が必須である。
図1に炭素の原子散乱因子fcarbonを示す[1][1] Z. Su and P. Coppens: Acta Cryst. A53 (1997) 749-762.。全電子(内殻電子+価電子)、内殻電子、価電子の寄与をそれぞれ黒色、青色、橙色で示す。通常の結晶構造因子の計算にはこの黒色の曲線で表される等方的な原子散乱因子を用いる。この原子散乱因子は、主に低角領域sinθ/λ < 0.5 Å-1に値を持つ価電子と、高角で原子全体の散乱因子とほぼ重なる内殻電子との和となっている。この散乱因子の振る舞いは、原子の持つ電子の空間分布を反映している。実験室系の特性X線を用いた単結晶回折実験の場合、回折データが測定可能な範囲はsinθ/λ < 2 Å-1程度であり、範囲外の回折データの情報は得られない。このとき、内殻電子数に対して価電子数の割合が多い軽元素の場合は、軌道混成によって結合に寄与する価電子密度分布がX線回折強度に比較的大きく寄与する。すなわち、大きな異方性を持った電子雲の平均値が原子位置となる。また、実験で得られる|Fobs(K)|は位相の情報を含んでいないため、電子密度解析に必要な位相項を計算構造因子Fcal(K)/|Fc(K)|から求めることにも大きく影響する。これらの問題は特に軽元素を多く含む分子性結晶の精密構造解析や電子密度解析を行う際に注意する必要がある。
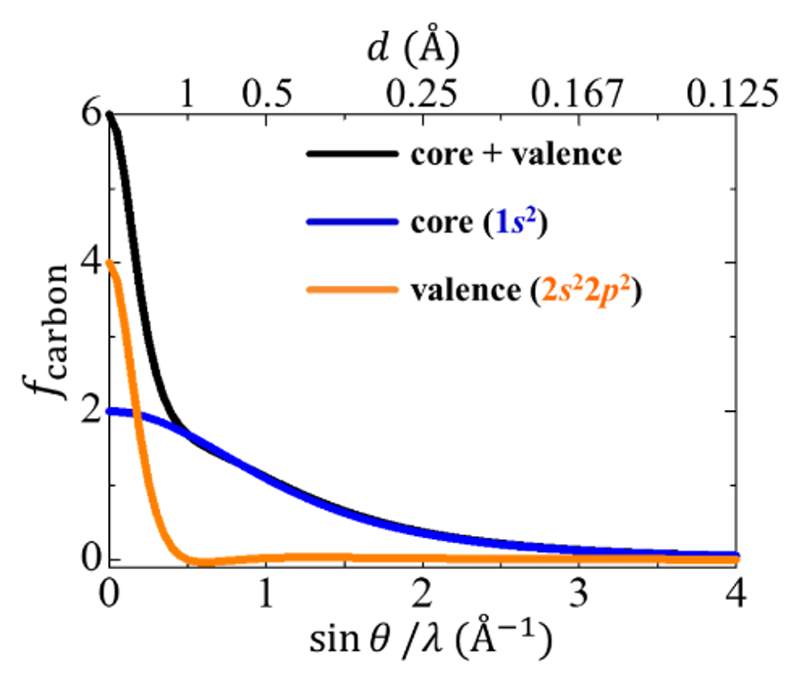
図1 炭素の原子散乱因子。黒線が全電子、青線が内殻電子(1s2)、橙線が価電子の寄与を表す。
改めて図1を見ると、炭素の場合には価電子の情報をほとんど含まないsinθ/λ > 0.5 Å-1の高角領域の回折データを用いて精密化すれば、原子配置に特化した構造モデルFcal(K)を十分信頼できる精度で決定可能であることに気がつく。この精密化手法は高角解析と呼ばれる[2][2] 橋爪大輔: 日本結晶学会誌 56 (2014) 313-318.。このために必要な実験条件は、価電子の寄与をほとんど無視し得るd値の反射強度を観測可能な短波長のX線を用いることである。この高角反射強度を用いた精密化によって得られた位相項PをP = Fcal(K)/|Fcal(K)|として与えることで、逆フーリエ変換による電子密度の再構成を行うことができる。しかし、よく知られているようにフーリエ合成の打ち切りの影響で、電子密度分布の情報を抽出できない。そこで、我々は物質の軌道状態の観測を目指し、コア差フーリエ合成(core differential Fourier synthesis; CDFS)法による電子密度解析手法を提案した[3-5][3] S. Kitou et al.: Phys. Rev. Lett. 119 (2017) 065701.
[4] S. Kitou et al.: Crystals 10 (2020) 998.
[5] S. Kitou et al.: Phys. Rev. Research 2 (2020) 033503.。CDFS法による価電子密度ρv(r)の計算法を(1)式に示す。
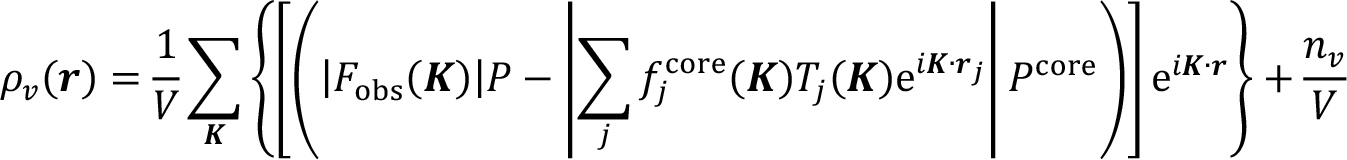 |
(1) |
ここで、ユニットセルの体積をV、各原子のユニットセル内での部分座標の位置ベクトルをrj(j = 1...N, 0 ≤ |rj| < 1)、散乱ベクトルKとし、Tj(K)はj番目の原子変位パラメータ(通称:熱振動因子)である。fjcore(K)はj番目の原子の内殻電子の寄与のみの原子散乱因子である(図1の青線に対応)。Pは全回折データで決めた位相因子であり、PcoreはPcore = ![]() (K)/|
(K)/|![]() (K)|で与えられる。また、nvはユニットセル内の価電子数に対応する。CDFS法では実験的に得られる全電子の情報をもつ|Fobs(K)|から、計算した内殻電子の寄与を差し引き、その値を逆フーリエ変換することで、価電子密度分布の情報を効率よく抽出する。このとき、残ったfjvalence(図1の橙色の線)はsinθ/λ > 0.5 Åで有限の値をほとんど持たないため、(1)式の計算で得られる価電子密度ρv(r)には打ち切りの影響がほとんど現れない。
(K)|で与えられる。また、nvはユニットセル内の価電子数に対応する。CDFS法では実験的に得られる全電子の情報をもつ|Fobs(K)|から、計算した内殻電子の寄与を差し引き、その値を逆フーリエ変換することで、価電子密度分布の情報を効率よく抽出する。このとき、残ったfjvalence(図1の橙色の線)はsinθ/λ > 0.5 Åで有限の値をほとんど持たないため、(1)式の計算で得られる価電子密度ρv(r)には打ち切りの影響がほとんど現れない。
この手法を用いた軌道状態の観測の成果は、無機系・有機系についていくつか報告した[4,5][4] S. Kitou et al.: Crystals 10 (2020) 998.
[5] S. Kitou et al.: Phys. Rev. Research 2 (2020) 033503.。この手法の有効性を確認するために、遷移金属の軌道秩序状態について精密に議論した。軌道秩序と磁性との関連は昔から注目度が高く、偏極中性子散乱、放射光共鳴X線散乱など直接観測の実験報告が複数ある。このCDFS法で得られた軌道状態がこれらの過去の報告と定性的に同じであるだけでなく、定量的にも高い精度を持つことを検証した。一方で、自由度を維持している状態、すなわち縮退軌道の電子密度分布についてはほとんど実験観測の報告がなく、縮退軌道の電子密度が異方性を持っていることはあまり積極的に議論されることはない。そこで、本質的な電子状態の観測が可能かどうかを判定するため、第一原理計算が難しい縮退軌道の電子状態の観測に挑戦した。
3. 遷移金属3d軌道の縮退軌道の2電子占有状態
ここで取り上げるスピネル型酸化物FeV2O4ではFeO4四面体とVO6八面体が三次元的なネットワークを形成している。高温相の晶系はcubic、空間群は![]() (No.227)であり、対称性が非常に高い(図2(a))。形式価数はFeが2+、Vが3+であり、それぞれ6個、2個の3d電子を持つ(図2(b))。閉殻になっていない電子配置にも関わらず、この系はMott絶縁体であり電荷の自由度は失っている。しかし、縮退軌道が生じている部分占有の電子配置の場合、軌道自由度が残存する。強い電子相関と構造由来の幾何学的フラストレーションが存在するため、スピン・軌道・格子の自由度が複雑に絡み合い、降温過程において三回の構造・磁気相転移を示す[6-10][6] S. H. Lee et al.: J. Phys. Soc. Jpn. 79 (2010) 011004.
(No.227)であり、対称性が非常に高い(図2(a))。形式価数はFeが2+、Vが3+であり、それぞれ6個、2個の3d電子を持つ(図2(b))。閉殻になっていない電子配置にも関わらず、この系はMott絶縁体であり電荷の自由度は失っている。しかし、縮退軌道が生じている部分占有の電子配置の場合、軌道自由度が残存する。強い電子相関と構造由来の幾何学的フラストレーションが存在するため、スピン・軌道・格子の自由度が複雑に絡み合い、降温過程において三回の構造・磁気相転移を示す[6-10][6] S. H. Lee et al.: J. Phys. Soc. Jpn. 79 (2010) 011004.
[7] T. Katsufuji et al.: J. Phys. Soc. Jpn. 77 (2008) 053708.
[8] G. J. MacDougall, V. O. Garlea, A. A. Aczel, H. D. Zhou, and E, Nagler: Phys. Rev. B 86 (2012) 060414(R).
[9] Y. Nii et al.: Phys. Rev. B 86 (2012) 125142.
[10] D. Dey, T. Maitra and A. Taraphder: Phys. Rev. B 93 (2016) 195133.。
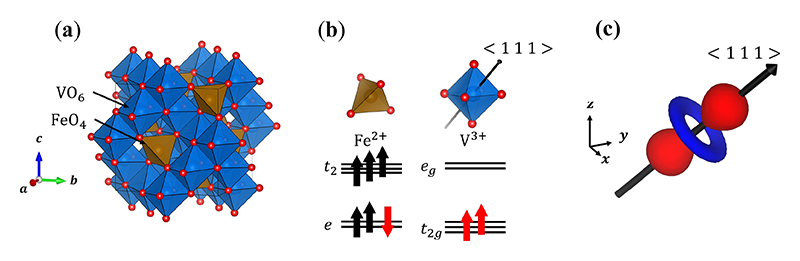
図2 (a) FeV2O4の結晶構造、(b) 結晶中のFe2+及びV3+の最も対称性が高い場合の電子配置、(c) <1 1 1>方向を量子化軸に持つ φ1 = (|yz〉+|zx〉+|xy〉)/![]() 軌道。
軌道。
高温(140 K以上)のcubic相においては、対称性からFeとVの2サイトにスピンと軌道の自由度を有しており(図2(b)の赤矢印)、これらが協奏することで逐次相転移が起こると考えられている。しかし、これまで実験と理論の両面から多くの研究がなされているにも関わらず、複雑に自由度が絡み合うために本系の各相における詳細な電子状態はいまだ統一的な理解に至っていない。独立な自由度が多数共存していることから、同型の物質との比較を行うことによって相転移機構の類推がなされている。
V3+の持つ2つの3d電子はt2g軌道を部分的に占有するため、Vのサイトには軌道自由度が存在する。しかし、実際はユニットセル内のVO6八面体は正八面体ではない。Vのサイトシンメトリーは.![]() であり、3回回転軸を1本しか有しない制約のため、八面体は3回軸方向に歪む(D3d歪み)ことのみが許され、3回軸である<1 1 1>方向に延びている。この時、<1 1 1>が量子化軸となるため、縮退していた3軌道の中で1軌道の波動関数だけは一意に決めることができ、
であり、3回回転軸を1本しか有しない制約のため、八面体は3回軸方向に歪む(D3d歪み)ことのみが許され、3回軸である<1 1 1>方向に延びている。この時、<1 1 1>が量子化軸となるため、縮退していた3軌道の中で1軌道の波動関数だけは一意に決めることができ、
| (2) |
となる(図2(c))。なお、x, y, zは結晶軸a, b, cとそれぞれ同じ方向に定義する。一方、残りの二重縮退した軌道は、φ1を含めた3つの軌道がお互いに直交するという条件しか課されないため一意には決まらない。この二重縮退と1軌道のエネルギー準位は、どちらが安定化するか計算方法の違いによって対照的な結果が得られる。これは、D3d歪みが<1 1 1>方向に延びながら、<1 1 1>方向の正三角形の面積を小さくするように歪むため、2種類の結晶場の効果が鬩ぎ合うことが原因である。もちろん歪が小さいために、D3d歪みによるt2g軌道の分裂幅が小さく、熱的な揺らぎによりt2g軌道が縮退したままと見なせる可能性もある。以上のように、直感的には電子状態を区別することが困難であり、この系の逐次相転移の出発点である高温cubic相の軌道状態は自明ではない。そこで、実験による軌道状態の決定を試みた。
4. 回折実験条件と解析結果
使用した試料は東京大学の有馬孝尚先生に提供していただいた試料を加工したもので、サイズは約40 × 40 × 10 μm3である。X線回折実験はSPring-8 BL02B1で行った。温度制御にはN2吹き付け装置を使用し、cubic相の160 Kで測定した。入射X線のエネルギーは40 keV(λ = 0.3100 Å)であり、検出器として光子計数型のCdTe-PILATUSを用いた。この検出器による強度積分の抽出は、従来装置に装備されていたイメージングプレート(IP)よりも高い精度で可能である。IPでは行うことができなかった波長選択によるバックグラウンド強度の低減は、埋もれやすい低強度の反射に精度の差が顕著に表れることが期待される。
この新しい検出器を用いて価電子密度分布解析を行ってみたところ、測定条件によって異なる結果を示すことが分かってきて、極めて困った事態となった。このことを示したのが図3である。初期のころは、以前のIPの測定条件と同じΔω = 1°で回折像を収集した。これを解析した結果が図3(a)である。このグラフは縦軸が観測結晶構造因子|FO|の二乗、横軸が計算構造因子FCの二乗である。目盛が対数表示になっていることに注意されたい。回折強度が小さい領域では、明らかに観測強度が小さくなっており統計誤差も大きい。PILATUS検出器は最速500 Hz(2 ms)でデータを読み出すことができるため、この機能を利用したFine slice測定を行った。すなわち、Δω = 0.1°に分解して測定を行うことで1つの回折点を複数フレームに分割して記録することができ、回折点のロッキングカーブを分解して得られる。解析用ソフトCrysAlisPro[11][11] Agilent. CrysAlis PRO. Agilent Technologies Ltd, Yarnton, Oxfordshire, England (2014).を用いて、この測定データから回折強度抽出して構造解析した結果が図3(b)である。|FO|2-|FC|2プロットの線形性が上がっているだけでなく、挿入図に示された価電子密度分布が明らかに異なっている。再現性及び他の標準結晶の測定・解析を繰り返した多岐にわたる測定条件の検証実験により、図3(b)の電子密度分布が本質的な結果であることを確認した。
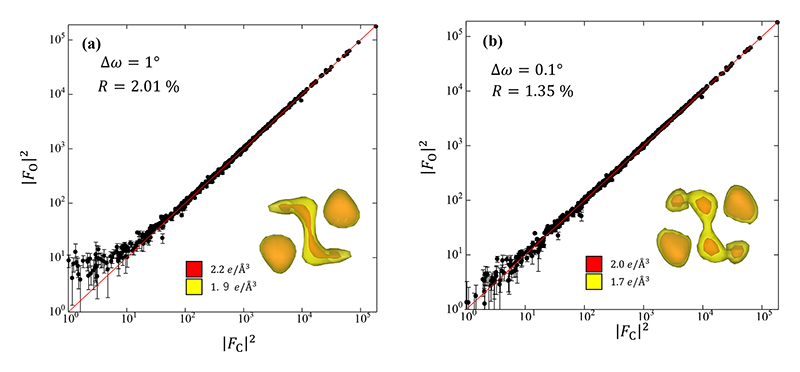
図3 PILATUSを用いた2種類の測定法の|FO|とCrysAlisProによる解析結果FCによる|FO|2-|FC|2プロット。(a) Δω = 1°の測定の場合、(b) Δω = 0.1°の場合。グラフ中の挿入図はV3+の価電子密度分布。
ここでは、明らかに異なる結果を並べて示したため、Fine slice測定が適切であることは自明のように感じるかもしれない。しかし、このような差異の原因は実験条件を精密に検証するまで明らかにすることができなかった。特に得られた価電子密度分布が1つしかない場合に、解析結果が正しいか否かを判断することは極めて困難である。あまりに煩雑になるためここでは詳細を省略するが、数え落とし補正や、検出器上の半導体素子の不安定性などについて検討し、現在では価電子密度分布解析を安定的に行える条件をほぼ洗い出すことができている。2022年現在もこれらの件について、施設側の担当者と検討及び対応を進めている。
5. Vの電子軌道状態
さて、得られたVサイトの価電子密度分布を量子力学的に理解するために、二重縮退した軌道を定義する。3節で述べた通り、φ2, φ3は一意に決めることができない。そこで、仮にφ2 = C1'|yz〉 + C2'|zx〉 + C3'|xy〉と定義すると、パラメータはC1', C2', C3'の3つである。3軌道の直交性からφ2だけ決まればφ3はφ1とφ2の外積から自動的に決まるため、3つのパラメータで十分で、課される条件式は、
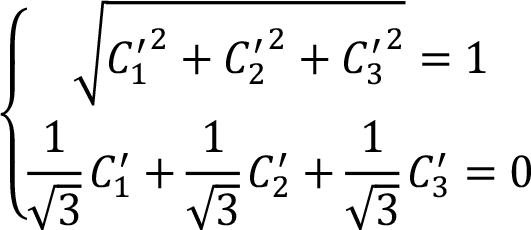 |
(3) |
の2式である。それぞれ規格化条件とφ1との直交条件である。3つの未知数に対して条件が2つなので、パラメータは一意に決まらない。例えば、φ2, φ3を(3)式を満たす特殊解として
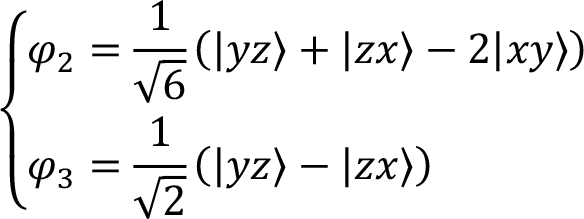 |
(4) |
を用いればよい。また、電子密度と比較するために、|φi|2 (i = 1,2,3)を用いる。CDFS法で得られる情報は電子密度であり、波動関数の位相情報が失われていることに注意が必要である。
すでに実験結果として異方的な価電子密度分布が得られているため、以上の波動関数を用いて実際に電子状態を比較検討する。考えるべき電子軌道状態の可能性としては、(i)t2gの分裂が熱エネルギーより小さく見かけ上三重縮退を維持している場合、(ii)φ1に対して二重縮退が安定化した場合、(iii)逆に二重縮退が不安定化した場合、の3パターンがある。ここでは研究上最も面白かった検証過程を省くが、結論として(iii)の状態が実現しておりφ1軌道を1電子、縮退したφ2, φ3軌道を1電子が占有していることがわかった。この「二重縮退上に1電子が存在する」とは縮退軌道を等確率に占有すると考えられ、|φ1|2 + ![]() |φ2|2 +
|φ2|2 + ![]() |φ3|2と記述される。これを、実空間に描画すると図4(b)の価電子密度分布が得られる。これは、実験結果である図4(a)を驚くほど忠実に再現している。すなわち、Vの軌道状態は、1つの電子が安定化した軌道を占有し、もう1つの電子がフント則により高エネルギーの二重縮退上に上がり、縮退した軌道を等確率で占有すると理解される。この結果は、軌道自由度を持つ軌道状態を決定した初めての例である。ここでは、紙面の制約から省略するが、Feについても全く同様に解析できて、縮退軌道を含むFe2+: 3d6軌道状態を反映した異方的な価電子密度分布となっている。
|φ3|2と記述される。これを、実空間に描画すると図4(b)の価電子密度分布が得られる。これは、実験結果である図4(a)を驚くほど忠実に再現している。すなわち、Vの軌道状態は、1つの電子が安定化した軌道を占有し、もう1つの電子がフント則により高エネルギーの二重縮退上に上がり、縮退した軌道を等確率で占有すると理解される。この結果は、軌道自由度を持つ軌道状態を決定した初めての例である。ここでは、紙面の制約から省略するが、Feについても全く同様に解析できて、縮退軌道を含むFe2+: 3d6軌道状態を反映した異方的な価電子密度分布となっている。
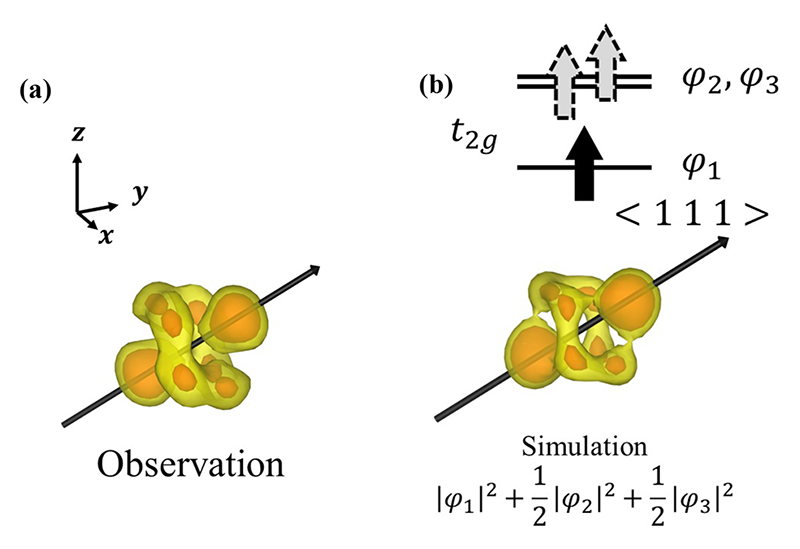
図4 (a) CDFS解析によるV3+の価電子密度分布(方向の異なる図3(a)と同じ解析結果)、(b) 二重縮退したφ2, φ3軌道に1電子が等確率に存在する|φ1|2 + ![]() |φ2|2 +
|φ2|2 + ![]() |φ3|2のシミュレーション結果(本文参照)。
|φ3|2のシミュレーション結果(本文参照)。
Vサイトの解析結果は、軌道自由度のとらえ方に対して新たな知見を与える。|φ1|2 + ![]() |φ2|2 +
|φ2|2 + ![]() |φ3|2とは、1電子がφ1を、φ2とφ3を各々1/2電子が占有していることを示している。これは、X線回折が結晶中のユニットセルの時間・空間平均であることを反映している。つまり、CDFS法によって得られた電子軌道の状態も時間・空間平均であり、結晶中のあるユニットセル中のVサイトが、ある瞬間にφ2かφ3を占有している電子が存在し、その時間・空間平均として1/2という係数が表れると解釈される。しかし、3節で述べた通り、二重縮退した軌道の波動関数は一意に決まらないため、シミュレーションで用いたφ2, φ3は条件を満たす1つの組み合わせでしかない。φ1との直交性を考慮すれば、二重縮退した軌道の波動関数は
|φ3|2とは、1電子がφ1を、φ2とφ3を各々1/2電子が占有していることを示している。これは、X線回折が結晶中のユニットセルの時間・空間平均であることを反映している。つまり、CDFS法によって得られた電子軌道の状態も時間・空間平均であり、結晶中のあるユニットセル中のVサイトが、ある瞬間にφ2かφ3を占有している電子が存在し、その時間・空間平均として1/2という係数が表れると解釈される。しかし、3節で述べた通り、二重縮退した軌道の波動関数は一意に決まらないため、シミュレーションで用いたφ2, φ3は条件を満たす1つの組み合わせでしかない。φ1との直交性を考慮すれば、二重縮退した軌道の波動関数は
| (5) |
と、任意の位相因子θを用いて表現される(図5(a))。単純な計算であるが、この|φ1|2 + ![]() |φ2'|2 +
|φ2'|2 + ![]() |φ3'|2 は|φ1|2 +
|φ3'|2 は|φ1|2 + ![]() |φ2|2 +
|φ2|2 + ![]() |φ3|2と同じ価電子密度分布を与える。すなわち、位相因子θをどのようにとっても、直交するφ2', φ3'の組み合わせの電子密度は同じ異方性を与える(図5(b))。
|φ3|2と同じ価電子密度分布を与える。すなわち、位相因子θをどのようにとっても、直交するφ2', φ3'の組み合わせの電子密度は同じ異方性を与える(図5(b))。
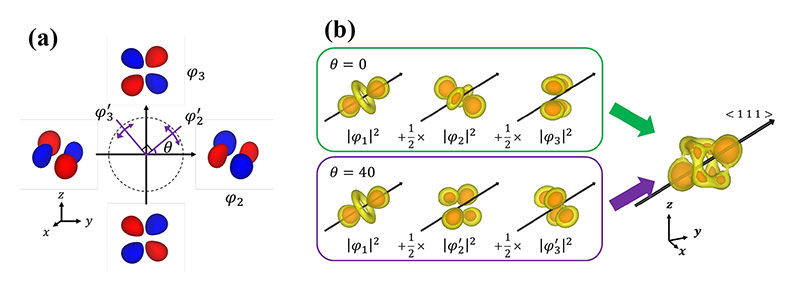
図5 (a) 互いに直交するφ2, φ3の位相の関係。(b) θ = 0°の場合とθ = 40°の場合のシミュレーションの結果。θがどのような値をとってもシミュレーション結果は同じになる。
量子力学的には、このθは時間・空間的に揺らいでいる。したがって、CDFS法で観測された価電子密度分布は本質的に
| (6) |
である。Nは結晶内のVサイトの数であり莫大な数となる。jはj番目のVサイト、tは時間である。これをθの積分と捉えると、
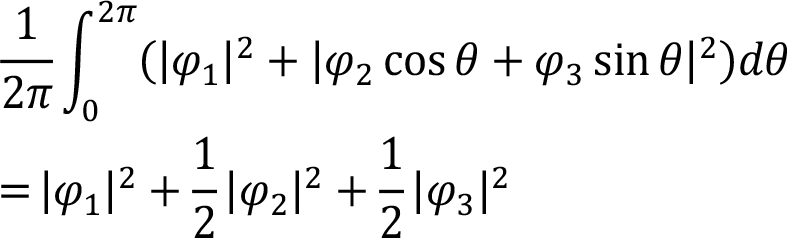 |
(7) |
となり、解析結果と対応する。つまり、縮退軌道の電子状態は時間・空間的に揺らいでおり、この揺らぎこそが軌道自由度を持つことの本質である。
なお、この結論は少し飛躍があることにお気づきであろうか?回折実験では空間的な不均一なのか時間的揺らぎなのかを区別できないことを式(7)は示しており、「揺らぎ」の存在は演繹できない。この系においては、降温によって構造相転移を起こすoriginが軌道自由度の消失であることを考えれば、空間的に不均一に軌道自由度を失っている一種の軌道ガラス状態を形成しているとは考えにくい。また、構造相転移においてJahn-Teller歪の形成を伴う電子格子相互作用の存在を考えれば、相転移近傍におけるフォノンのソフト化が観測される筈である。我々は、放射光X線非弾性散乱実験によってこのソフト化の観測にも成功し、時間・空間的な揺らぎの平均を見ている仮説を検証した。詳細は文献[12][12] T. Manjo et al.: Materials Advances 3 (2022) 3192-3198.を参照されたい。
6. 結びにかえて
以上のように、PUの期間中に到達した超精密解析による価電子密度分布解析の一例を紹介させて頂いた。現在も、他の多くの系の価電子密度分布解析を進めており、順次成果を公開していく。単結晶回折実験には、異方的な吸収補正や、多重散乱、同時反射、消衰効果など多くの補正が必要であると教科書的に謳われており、実際我々もこれらの補正が必要な側面に多々遭遇している。しかしながら、現状ではこれらの単結晶回折における原理的な困難よりも、例えば測定条件の安定度、検出器の特性など、多くの系統誤差が問題になることが多く、SPring-8の高品質X線源の特性を十分活かした解析に辿り着いていないのではないかと危惧してきた。そのような中で、今回紹介したような実験室系とは質的に異なる解析が可能であることを示すことに成功した反面、PUで用意されたビームタイム期間のすべてを条件探索に費やさざるを得なかったことは痛恨の極みである。我々は、PU申請時の研究テーマにあるオペランド計測についてもUV照射による光電気伝導系、または光貯蔵系について様々な実験をかなりのシフト数を用いて試みた。しかしながら、これらの照射による変化は、励起光の有無によらない大きな統計誤差に埋もれてしまい、現行では確度のある結果は得られていないと考えている。一方で、光照射時の破砕が暗闇中では変形のみ生じるという特異な単結晶ZnSの回折実験を行ったところ、単結晶中の転位が光の有無によって異なることを突き止めたが、いわば巨視的な結晶の変化を微視的な不完全性として解釈できるというレベルに留まっている。
将来的にさらに施設・装置などの高度化が進めば、現状での最先端測定が標準測定となる日も遠くないと期待している。この価電子密度分布の直接観測手法は、多重極限下や外場応答に対応するオペランド計測にも適用できるように、現在も施設との協力のもとに開発を推し進めている。
謝辞
本研究は、多くの方々との共同研究であるが、主な共同研究者は有馬孝尚(東大新領域)、勝藤拓郎(早大理工)、杉本邦久(JASRI/SPring-8・現近大)、鬼頭俊介(名大院工・現理研)、原武史(名大院工)である。
参考文献
[1] Z. Su and P. Coppens: Acta Cryst. A53 (1997) 749-762.
[2] 橋爪大輔: 日本結晶学会誌 56 (2014) 313-318.
[3] S. Kitou et al.: Phys. Rev. Lett. 119 (2017) 065701.
[4] S. Kitou et al.: Crystals 10 (2020) 998.
[5] S. Kitou et al.: Phys. Rev. Research 2 (2020) 033503.
[6] S. H. Lee et al.: J. Phys. Soc. Jpn. 79 (2010) 011004.
[7] T. Katsufuji et al.: J. Phys. Soc. Jpn. 77 (2008) 053708.
[8] G. J. MacDougall, V. O. Garlea, A. A. Aczel, H. D. Zhou, and E, Nagler: Phys. Rev. B 86 (2012) 060414(R).
[9] Y. Nii et al.: Phys. Rev. B 86 (2012) 125142.
[10] D. Dey, T. Maitra and A. Taraphder: Phys. Rev. B 93 (2016) 195133.
[11] Agilent. CrysAlis PRO. Agilent Technologies Ltd, Yarnton, Oxfordshire, England (2014).
[12] T. Manjo et al.: Materials Advances 3 (2022) 3192-3198.
(3)成果リスト(査読付き論文)
SPring-8利用研究成果登録データベースに登録済みで、PU課題番号が関連づけられた査読付き論文のみを掲載します(その他、PUとして支援した一般課題の発表論文やポスター発表、受賞歴など多数の成果がありますが、掲載スペースの都合上割愛しています)。
[1] SPring-8 Publication ID = 40648 S. Kitou et al.: "Collapse of the Simple Localized 3d1 Orbital Picture in Mott Insulator" Physical Review Research 2 (2020) 033503.
[2] SPring-8 Publication ID = 40836 S. Kitou et al.: "Direct Observation of Molecular Orbitals Using Synchrotron X-ray Diffraction" Crystals 10 (2020) 998.
[3] SPring-8 Publication ID = 41434 T. Nakamura et al.: "Tetramethyltetrathiafulvalene [(NbOF4)−]∞: One-Dimensional Charge Transfer Salt with an Infinite Anion Chain" Inorganic Chemistry 60 (2021) 5206-5211.
[4] SPring-8 Publication ID = 41820 S. Kitou et al.: "Complex Changes in Structural Parameters Hidden in the Universal Phase Diagram of the Quasi-One-Dimensional Organic Conductors (TMTTF)2X (X = NbF6, AsF6, PF6, and Br)" Physical Review B 103 (2021) 184112.
[5] SPring-8 Publication ID = 43096 T. Manjo et al.: "Do Electron Distributions with Orbital Degree of Freedom Exhibit Anisotropy?" Materials Advances 3 (2022) 3192-3198.
名古屋大学大学院 工学研究科
〒464-8603 名古屋市千種区不老町1
TEL : 052-789-4453
e-mail : hiroshi.sawa@cc.nagoya-u.ac.jp








