Volume 27, No.3 Pages 187 - 192

1. 序論
　我々の体は数十兆個にもおよぶ細胞から形成されている。細胞の一つ一つは細胞膜で覆われ、外部から栄養素を取り込み、老廃物を廃棄することにより多様な細胞機能を発現し、我々の生命が維持されている。細胞膜は細胞内外を連携する重要な境界であり、物質輸送に十分な流動性を有している必要がある一方で細胞の形態を維持するだけの十分な剛性が必要である。このような二つの相反する要求を満たすため、自然は脂質分子を細胞膜の基本成分として採用している。
　脂質分子は一般的に両親媒性の分子であり、一分子に親水基と疎水基を併せ持つ。親水基には水酸基、リン酸基などの多様性があり、疎水基にはアシル鎖長、炭化水素鎖飽和度などの多様性がある^[1][1] T. Harayama and H. Riezman: Nat. Rev. Mol. Cell Biol. 19 (2018) 281-296.。細胞膜は多成分系で、様々な脂質分子が異なる組成で混合することにより多様な膜特性を調整していると考えられている。現在までに4万種を超える化学構造の異なる脂質分子が同定されており^[2][2] http://www.lipidmaps.org/、細胞膜やゴルジ体あるいはミトコンドリアなどの異なった細胞小器官では異なった脂質分子が異なった組成で膜を形成する^[3][3] G. van Meer, D. R. Voelker and G. W. Feigenson: Nat. Rev. Mol. Cell Biol. 9 (2008) 112-124.。しかしながら、何故その様に多種類の分子が必要なのか、その物理的要因はまだ十分に理解されていない。
　最もよく知られている大きな特徴は脂質分子疎水鎖の融解転移である。典型的なリン脂質の一種であるdimyristoylphosphocholine（DMPC）は2本のアシル鎖を持ち、その融解転移温度はT_m = 297 Kである。図1に模式的に示す様にT < T_mではアシル鎖が凍結した構造を取り、その運動性が下がる。一般的に固体膜（あるいは脂質ゲル相）と呼ばれる状態である。一方、T > T_mではアシル鎖が融解することにより分子の運動性が上がり、膜は液体膜（あるいは脂質液体相）状態にある。生命活動は液体膜上で繰り広げられていることが知られているが、液体膜中でも様々な構成分子がドメインなどのヘテロな構造を有し、タンパク質などが様々な生命活動に寄与している。

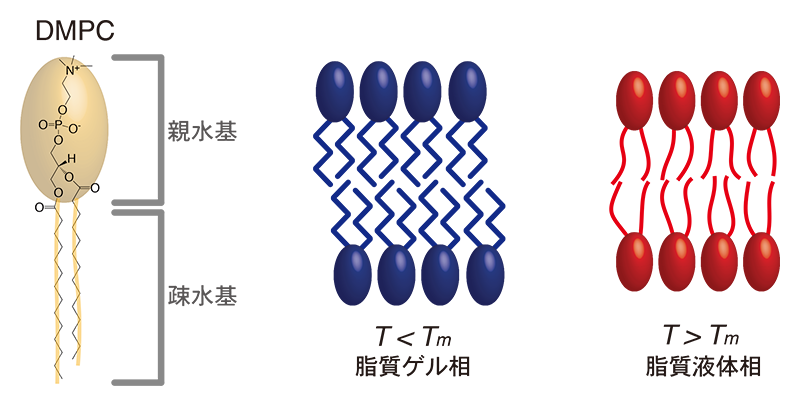
図1　脂質分子の模式図（左）と温度変化による脂質アシル鎖融解転移が誘起する脂質ゲル相と液体相。

　例えば、膜タンパク質が膜上の機能発現サイトへ運ばれ、形態を変化させながら役割を果たそうとする時、膜が固体であれば輸送も変形もできずに生物は機能しない。生命現象は様々なプロセスの連鎖からなるので、タンパク質の輸送や変形の速度はこれらのプロセスの速度論を考察する上で極めて重要である。生物は気温の変化に敏感に反応し膜の流動性を一定に保とうとする機能を有している（恒流動性適応）。膜の構成成分組成を変化させることによって流動性を一定に保つのである。このような膜の流動性の本質は膜の粘性であると考えられるが、では、何が膜の粘性を支配しているのであろうか。
　脂質膜は脂質分子が疎水基を内側に、親水基を外側にむけた二分子分の厚み、約5 nmを有している。このように非常に薄い膜の粘性係数を測定することはそれ自体が実験的な困難を伴う。10 μm程度の大きさのベシクル表面にナノ粒子を吸着させ重力による沈降速度を計測することにより膜の粘性率を計算するsurface viscosimetry^[4][4] R. Dimova, C. Dietrich, A. Hadjisky, K. Danov and B. Pouligny: Euro. Phys. J. B 12 (1999) 589-598.、基板表面にμmサイズの半球を吸着させ半球上の流動場変化をベシクル周辺の液体の流動場から見積もることによって膜の粘性率を見積もる方法^[5][5] A. R. Honerkamp-Smith, F. G. Woodhouse, V. Kantsler and R. E. Goldstein: Phys. Rev. Lett. 111 (2013) 038103.、膜に蛍光標的などを吸着させその並進や回転の拡散運動から計測する方法^[6,7][6] T. T. Hormel, S. Q. Kurihara, M. K. Brennan, M. C. Wozniak and R. Parthasarathy: Phys. Rev. Lett. 112 (2014) 188101.
[7] Y. Sakuma, T. Kawakatsu, T. Taniguchi and M. Imai: Biophys. J. 118 (2020) 1576-1587.、電界によるベシクル変形からの回復時間が膜の粘性に依存することを利用した計測方法^[8][8] H. A. Faizi, R. Dimova and P. M. Vlahovska: Biophys. J. 121 (2022) 910-918.など、顕微鏡を使った多数の測定方法が提案されてきている。これらの方法はほぼ全てが非平衡状態における測定であり、膜に何らかの摂動を加えることによる測定である。また観測の時間空間スケールが比較的大きいことから、これらの手法は膜の粘性をマクロなパラメータとして計測している。一方、中性子散乱を使い、メゾスコピックスケール（10 nm程度）における100 ns程度の熱平衡の揺らぎ運動から膜の粘性を計測する方法が提案されている^[9,10][9] M. Nagao, E. G. Kelley, R. Ashkar, R. Bradbury and P. D. Butler: J. Phys. Chem. Lett. 8 (2017) 4679-4684.
[10] E. G. Kelley, P. D. Butler and M. Nagao: in Characterization of Biological Membranes–Structure and Dynamics, Ed. J. Katsaras, M. P. Nieh, F. A. Heberle, de Gruyter, Chap. 4 (2019) 131.。さらに、コンピュータシミュレーションを用いて膜に非平衡な流動変形を加えて膜の粘性を計算する方法なども開発されている^[11,12][11] S. A. Shkulipa, W. K. den Otter and W. J. Briels: Biophys. J. 89 (2005) 823-829.
[12] A. Zgorski, R. W. Pastor and E. Lyman: J. Chem. Theory Comput. 15 (2019) 6471-6481.。しかしながら、得られている膜の粘性率の大きさは測定手法に応じて異なり、数桁にわたって広く分布している。
　そこで本研究では膜の粘性の分子的な起源を探ることを目的とし、共鳴ガンマ線によるメスバウアー時間領域干渉計（Mössbauer Time Domain Interferometry; MTDI）法と中性子スピンエコー（Neutron Spin Echo; NSE）法を相補的に利用し、典型的なリン脂質分子の構造緩和運動を調べた^[13][13] M. Nagao et al.: Phys. Rev. Lett. 127 (2021) 078102.。

2. 液体の粘性と構造緩和
　一般に、液体の粘性の本質についての研究は盛んに行われている。通常の分子性液体の場合、分子間相互作用に基づく構造形成とその緩和がマクロな液体の粘性と関連していることが知られている。しかし、一般的な液体の粘性ですら様々な時間空間スケールに及ぶ複雑な分子間相互作用のため、その議論は複雑となる。Mezeiらは液体のガラス転移近傍での構造と運動がマクロな物性に及ぼす影響を調べた^[14][14] F. Mezei, W. Knaak and B. Farago: Phys. Rev. Lett. 58 (1987) 571-574.。また、Wuttkeらは、グリセロールの重心間相関の緩和時間とマクロな粘性が同一の温度依存性を示すことを実験的に明確にし、分子間の構造緩和がマクロな粘性の起源であることを示した^[15][15] J. Wuttke, W. Petry and S. Pouget: J. Chem. Phys. 105 (1996) 5177-5182.。より複雑な分子間相互作用を有するような系では、より長周期の構造相関が重要になるケースも見られるが、一般的には分子間の相互作用の強さが分子運動に対する抵抗となり、それがマクロには粘性として現れると考えることができる。液体におけるグリーン・久保理論は粘性の分子論的起源を応力テンソルの時間相関関数として理解する^[16,17][16] M.S. Green: J. Chem. Phys. 22 (1954) 398-413.
[17] R. Kubo: J. Phys. Soc. Jpn. 12 (1957) 570-586.。近年、山口はこの理論を適応して単純液体の構造緩和が液体の粘性の微視的起源であることを論じている^[18][18] T. Yamaguchi: J. Chem. Phys. 146 (2017) 094511.。本研究では、このような三次元液体で見られる粘性率ηと構造緩和の緩和時間τが絶対温度Tの変化に対してη~τTの関係に従う^[14][14] F. Mezei, W. Knaak and B. Farago: Phys. Rev. Lett. 58 (1987) 571-574.ことに着目し、脂質アシル鎖相関の構造緩和を基に二次元膜の粘性の議論を行った。

3. 実験
　本研究ではモデルリン脂質膜としてDMPCを水中に分散した多層膜ベシクルを用いた。X線散乱実験にはDMPCとH₂Oの混合系を、中性子散乱実験にはアシル鎖を重水素化したDMPC-d₅₄とD₂Oの混合系を用いた。DMPCの濃度は400 mg/mLとした。DMPC-d₅₄とD₂Oを中性子散乱に用いる理由は、H原子から生じる非常に強い中性子非干渉性散乱を抑制し、脂質アシル鎖間の相関を精度良く測定するためである。
　共鳴ガンマ線を用いたMTDI実験にはSPring-8のBL09XUに設置されたものを利用した。実験手法の詳細は文献^[19,20][19] M. Saito, R. Masuda, Y. Yoda and M. Seto: Sci. Rep. 7 (2017) 12558.
[20] 齋藤真器名、山口毅、長尾道弘：物理学会誌, in press.を参照いただきたい。ここでは簡単にその原理を紹介する。⁵⁷Fe原子核は放射光の入射によって共鳴ガンマ線を放射する。このガンマ線はエネルギー14.4 keV ± 4.7 neVという極めて単色性の高いビームである。この共鳴ガンマ線はおよそ140 nsの緩和時間で減衰する。このような⁵⁷Fe原子核を試料前後に設置し、それぞれ共鳴ガンマ線を発生させる。一方の共鳴ガンマ線のエネルギーをドップラーシフトによって変化させた場合、これら二つの⁵⁷Feから放射された共鳴ガンマ線は時間領域で干渉し、うなりを生じる。もし試料中で拡散などの運動によってガンマ線が散乱されると、時間領域でのうなりパターンが変化する。この変化を捉えることによって物質中の運動を観測するのがメスバウアー時間領域干渉計である。この手法では、放射光ストレージリングのバンチモード運転を利用し、バンチ間隔（SPring-8のFモード運転の場合およそ340 ns）の時間までのガンマ線の干渉の様子を観察できる。本実験での観測時間域はおよそ10 nsから300 nsであり、実験データは中間散乱関数 I(q,t) として取得される。ここで、qは散乱ベクトルの大きさ、tは時間である。
　一方、NSE法はMTDI法がカバーする時間領域よりも早い時間の運動観測に利用される。中性子はスピン自由度を有するため、中性子スピンを揃えた偏極中性子を利用できる^[21,22][21] F. Mezei: Z. Phys. 255 (1972) 146-160.
[22] 長尾道弘：波紋19 (2009) 42-48.。中性子スピンは磁場中で歳差運動を行うので、NSEでは偏極中性子の歳差運動を試料前後でちょうど反転するように磁場環境を設定しておく。これにより試料からの散乱が弾性散乱（散乱による中性子エネルギー変化がない散乱）であれば中性子の偏極率は散乱前後で変化しないが、非弾性散乱の場合には中性子のエネルギー変化に応じて偏極率が変化する。この偏極率変化は試料の中間散乱関数に直接比例することから系の運動の様子を知ることができる。NSE法の時間分解能は入射中性子の波長の3乗と歳差磁場の大きさに比例する。米国標準技術研究所に設置されたNSE装置では波長6 Åの中性子で数psから16 nsまでの時間領域をカバーできる。NSEとMTDIの組み合わせにより、psから100 nsの5桁にわたる分子運動にアクセスすることが可能であることを強調しておく。
　DMPCは疎水基として二本の飽和アシル鎖が、およそ5 Åの距離を取るように配列している。図2にJ-PARCに設置された大観を用いて測定したアシル鎖からの回折パターンを示すが、アシル鎖の相関に応じた散乱ピークがq ≈ 1.5 Å^-1に現れる^[13][13] M. Nagao et al.: Phys. Rev. Lett. 127 (2021) 078102.。DMPCはT_m = 297 K（DMPC-d₅₄はT_m = 294 K）にアシル鎖の融解転移温度をもち、これより低温の脂質ゲル相ではアシル鎖は秩序的に配置しているため、図中青シンボルで示す様にピークも鋭い。一方、高温の脂質液体相ではアシル鎖は融解し、ピークも図中赤で示した様に低角側へシフトするとともにブロードになる。この変化は脂質アシル鎖の構造状態を反映した結果であり、本研究ではこのピーク位置におけるダイナミクスの測定を行った。

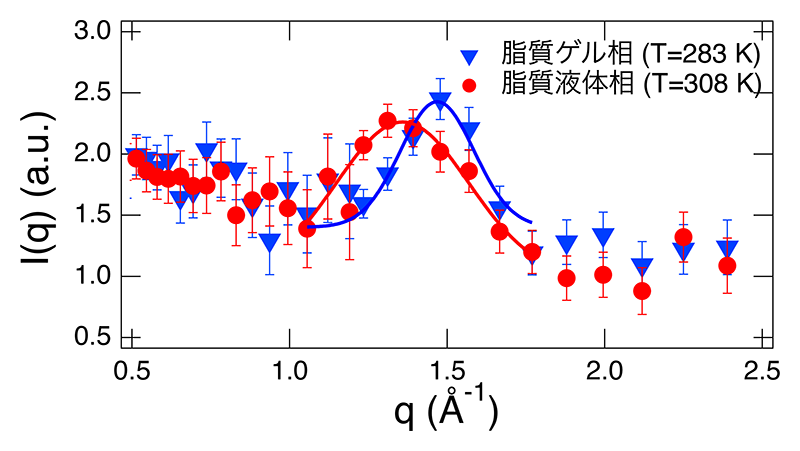
図2　D₂Oに溶解したDMPC-d₅₄が作る多層膜ベシクルのアシル鎖からの中性子回折パターン。http://dx.doi.org/10.1103/PhysRevLett.127.078102より許可を得て再掲載。

4. 結果と考察
　図3にNSEおよびMTDIにより測定された中間散乱関数 I(q,t)/I(q,0) の温度依存性を示す。ここで、NSEデータは重水からの散乱を取り除き、DMPC-d₅₄の動きだけを取り出した結果であり、t ≈ 0でI(q,t)/I(q,0)は1から始まっている。一方、MTDIデータはNSEデータにスムーズに繋がるように、右軸のスケールを調整してある。また、温度は融解転移点T_mからの相対温度で表示した。

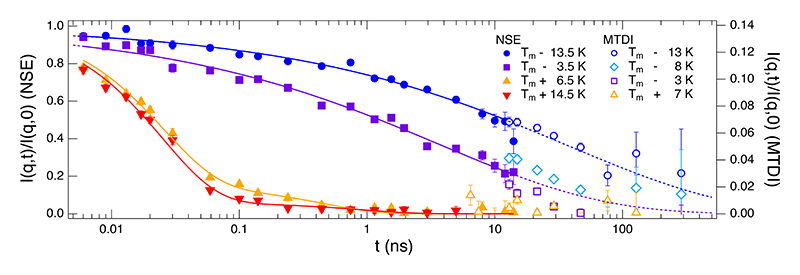
図3　NSE及びMTDIにより測定されたDMPC膜のアシル鎖の構造相関の中間散乱関数の温度依存性。http://dx.doi.org/10.1103/PhysRevLett.127.078102より許可を得て再掲載。

　T < T_mの脂質ゲル相ではアシル鎖は秩序的に並んでいると考えられてきたが、今回のNSEおよびMTDI測定により、psから数百nsの約5桁の時間オーダーにわたって緩やかに構造が緩和していることがわかった。NSE及びMTDIデータは拡張指数関数

によりフィットした。ここで、Cは係数で、NSEではC = 1、MTDIではフィットパラメータとした。τ_gel及びβは脂質ゲル相における緩和時間及び拡張指数である。一般的に、拡散運動の場合にはβ = 1となるが、本実験ではNSEデータの解析からβ ≈ 0.34の値が得られた。これは、ここで見られている緩和モードの緩和時間が不均一で、緩和時間の分布が非常に広いことを示している。また平均緩和時間を

により計算し、図4に〈τ_NSE〉及び〈τ_MTDI〉として示した。ここでΓ(x)はガンマ関数である。脂質ゲル相での平均緩和時間は転移点近傍では数十ns程度であるが、温度が下がるにつれて急激に大きくなり、T – T_m ≈ -15 Kでは数百nsまで遅くなる様子が捉えられた。

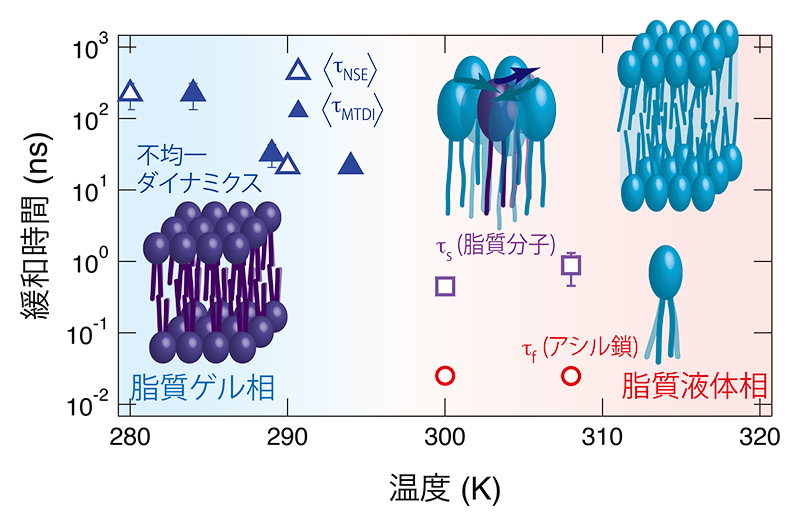
図4　NSE及びMTDI測定から得られた緩和時間の温度依存性。内装図は脂質分子の模式モデルであり、液体相での2種類の緩和がアシル鎖及び脂質分子の密度揺らぎに起因することを模式的に示す。

　一方、高温（T - T_m > 0）での緩和は脂質ゲル相とその様子が異なる。0.1 nsまでの早い時間スケールで見られる緩和と0.1 ns付近に見られる別の緩和モードの二段階の緩和が見られることがわかる。ここでは、二つの独立な緩和モードの重ね合わせを仮定し、

によりフィットした。これにより、速い緩和と遅い緩和のそれぞれの緩和時間τ_f及びτ_sを決定し、図4に示した。これらの緩和の緩和時間はあまり温度変化せず、τ_f ≈ 30 ps及びτ_s ≈ 500 ps程度と見積もられた。Rheinstädterらは基板に固定されたDMPC-d₅₄の重水膨潤膜のダイナミクスを中性子背面反射装置により測定し、アシル鎖相関ダイナミクスとしておよそ50 psの緩和時間を持つ運動が見られることを指摘している^[23][23] M. C. Rheinstädter et al.: Phys. Rev. Lett. 101 (2008) 248106.。本研究では運動を5桁にわたる時間領域で観測していることから、これらの時間領域に見られる緩和の描像をより詳細に決定できた。
　では、これら二つの緩和はどのような運動モードに対応するのであろうか。DMPCのアシル鎖は炭素数14の炭化水素鎖であり、三次元のテトラデカン（C₁₄H₃₀）の炭化水素鎖に非常に近い。山口はコンピュータシミュレーションによってテトラデカンの重心相関位置（q ≈ 1.4 Å^-1）における構造緩和の緩和時間が温度T_r = 298 Kでτ_r ≈ 3 ps程度であることを示している^[18][18] T. Yamaguchi: J. Chem. Phys. 146 (2017) 094511.。この緩和時間から計算された液体の粘性率は実験で得られているマクロな粘性率η_r ≈ 2.73 mPa•sとよく一致しており、シミュレーション結果が妥当であると考えられる。テトラデカンのアルキル鎖の構造緩和時間が3 psである一方、本実験から得られたDMPCアシル鎖の速い運動モードはこれよりも一桁遅い緩和時間を示している。これは、C₁₄の炭化水素鎖を二次元に閉じ込め、配向秩序と片端を親水基に結合するという構造上の制約を加えることによりアシル鎖自身の構造緩和が三次元液体状態の炭化水素鎖よりも一桁程度遅くなる、として理解できる。
　一方の遅い運動モードは脂質分子自身が再配置する構造緩和時間を表すと考えることができる。この場合、その緩和時間は脂質分子の拡散運動と関連していると考えられる。核磁気共鳴（NMR）法により求められている脂質分子の拡散係数はT = 308 KでD ≈ 1 × 10^-11 m²/sである^[24][24] A. Filippov, G. Orädd and G. Lindblom: Biophys. J. 84 (2003) 3079-3086.。拡散運動の緩和時間τ_Dはτ_D = 1/(Dq²)により計算することができ、我々の測定条件q ≈ 1.5 Å^-1では、τ_D ≈ 450 psと計算され、我々の測定結果（τ_s ≈ 500 ps）とよく一致する。
　上述した様に三次元液体の粘性係数と構造緩和時間の間にはη~τTの関係が成り立っている^[14][14] F. Mezei, W. Knaak and B. Farago: Phys. Rev. Lett. 58 (1987) 571-574.。この関係を二次元膜に拡張することによって膜の粘性率を見積もってみる。参照として、T_r = 298 Kにおけるテトラデカンの構造緩和の緩和時間τ_r ≈ 3 psと粘性率η_r ≈ 2.73 mPa•sを利用する^[18][18] T. Yamaguchi: J. Chem. Phys. 146 (2017) 094511.。脂質分子に対して得られている緩和時間τ_lipidに対して、以下の比例関係を用いることによって脂質分子の粘性率を計算することができる。

　この粘性率はDMPCが三次元に均一に分布している場合の粘性率と考えられる。一方、三次元物体を二次元に閉じ込めた場合の均一な二次元膜の表面粘度（あるいは膜粘度）はη_m ≈ d_m ηで表される^[25][25] E. Evans and E. Sackmann: J. Fluid Mech. 194 (1988) 553-561.。ここで、d_mは膜の厚みであり、DMPCの膜厚は以前の研究からおよそ3.5 nmである^[26][26] E. G. Kelley, P. D. Butler, R. Ashkar, R. Bradbury and M. Nagao: Proc. Natl. Acad. Sci. USA 117 (2020) 23365-23373.。これらの関係を利用して計算した膜粘度η_mの温度依存性を図5に示した。高温の脂質液体相では二つの緩和時間が観測されたが、そのうちの遅い緩和モードから計算された膜粘度は数桁にわたる広い膜粘度の文献値のほぼ中心に見られる。このことから、脂質分子の拡散に寄与する脂質分子間の相互作用が膜粘度の分子的起源であることが強く示唆される。一方、脂質ゲル相での膜粘度はこれまでに観測されたことがなく、本研究によって初めて求められた。脂質液体相に比較して一桁から二桁ほど大きな膜粘度を示すことが得られたが、これは、例えば膜の弾性率が脂質液体相と脂質ゲル相で一桁ほど異なること^[27][27] A. C. Woodka, P. D. Butler, L. Porcar, B. Farago and M. Nagao: Phys. Rev. Lett. 109 (2012) 058102.と整合する。

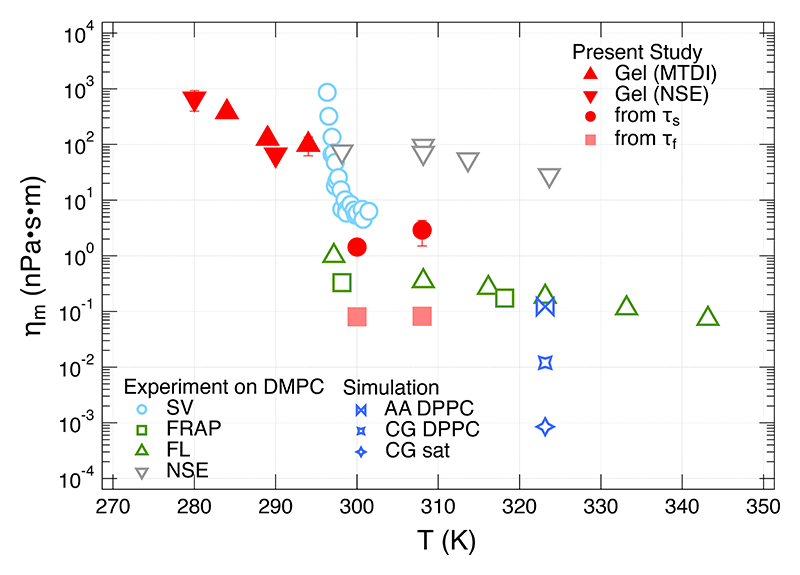
図5　様々な手法によって見積もられている脂質膜粘度。実験データはNSE^[9][9] M. Nagao, E. G. Kelley, R. Ashkar, R. Bradbury and P. D. Butler: J. Phys. Chem. Lett. 8 (2017) 4679-4684.、Surface Viscosimetry（SV）^[4][4] R. Dimova, C. Dietrich, A. Hadjisky, K. Danov and B. Pouligny: Euro. Phys. J. B 12 (1999) 589-598.、Fluorescent Recovery After Photobreaching（FRAP）^[28][28] R. Merkel, E. Sackmann and E. Evans: J. Phys. France 50 (1989) 1535-1555.及びFluorescence Life time（FL）^[29][29] Y. Wu et al.: Phys. Chem. Chem. Phys. 15 (2013) 14986-14993.、一方、シミュレーションデータは飽和脂質のcoarse grained（CG sat）^[11][11] S. A. Shkulipa, W. K. den Otter and W. J. Briels: Biophys. J. 89 (2005) 823-829.、DPPCモデルのcoarse grained（CG DPPC）^[30][30] W. K. den Otter and S. A. Shkulipa: Biophys. J. 93 (2007) 423-433.及び全原子シミュレーション（AA DPPC）^[12][12] A. Zgorski, R. W. Pastor and E. Lyman: J. Chem. Theory Comput. 15 (2019) 6471-6481.である。http://dx.doi.org/10.1103/PhysRevLett.127.078102より許可を得て再掲載。

5. 結語と展望
　脂質分子は細胞膜のモデル物質としてその物理化学的性質の理解が進められてきた。本研究では脂質膜粘性の分子論的起源に迫るべく、X線と中性子準弾性散乱により典型的な脂質アシル鎖の構造緩和をpsから数百nsという広い時間領域にわたって調べた。その結果、生物学的に不可欠な脂質液体相ではアシル鎖及び脂質分子の構造揺らぎの緩和時間を決定した。三次元液体の構造緩和と粘性の関係を二次元膜に拡張して計算した膜粘度から、脂質分子の構造揺らぎが粘性の起源であることが示唆された。一方、脂質ゲル相ではアシル鎖の非常に不均一な運動の描像が見出された。脂質ゲル相での膜粘度はこの様なヘテロな運動の平均緩和時間から算出され脂質液体相より一桁以上大きな粘性率を示すことがわかった。
　今後の方向性として、生物学的により重要であると考えられているステロール混合膜に見られる脂質液体秩序相のダイナミクスは非常に興味深い。また、4万種超の化学的に異なる脂質分子がどのように膜特性に関連するのかを知るためにも、X線や中性子を用いた原子、分子あるいは分子集合体スケールで見られる動的構造の理解が今後ますます興味深い研究対象になると考えられる。

謝辞
　本研究はElizabeth G. Kelley博士、Antonio Faraone博士、齋藤真器名准教授、依田芳卓主幹研究員、黒葛真行博士、高田慎一博士、瀬戸誠教授、Paul D. Butler博士との共同研究です。この場を借りてご協力に感謝します。放射光実験は高輝度光科学研究センターによって採択された実験課題番号2017B1512及び2018B1491についてSPring-8のBL09XUを用いて行われた。Access to the NGA-NSE instrument was provided by the Center for High Resolution Neutron Scattering, a partnership between the National Institute of Standards and Technology and the National Science Foundation under Agreement No. DMR-2010792.

参考文献
[1] T. Harayama and H. Riezman: Nat. Rev. Mol. Cell Biol. 19 (2018) 281-296.
[2] http://www.lipidmaps.org/
[3] G. van Meer, D. R. Voelker and G. W. Feigenson: Nat. Rev. Mol. Cell Biol. 9 (2008) 112-124.
[4] R. Dimova, C. Dietrich, A. Hadjisky, K. Danov and B. Pouligny: Euro. Phys. J. B 12 (1999) 589-598.
[5] A. R. Honerkamp-Smith, F. G. Woodhouse, V. Kantsler and R. E. Goldstein: Phys. Rev. Lett. 111 (2013) 038103.
[6] T. T. Hormel, S. Q. Kurihara, M. K. Brennan, M. C. Wozniak and R. Parthasarathy: Phys. Rev. Lett. 112 (2014) 188101.
[7] Y. Sakuma, T. Kawakatsu, T. Taniguchi and M. Imai: Biophys. J. 118 (2020) 1576-1587.
[8] H. A. Faizi, R. Dimova and P. M. Vlahovska: Biophys. J. 121 (2022) 910-918.
[9] M. Nagao, E. G. Kelley, R. Ashkar, R. Bradbury and P. D. Butler: J. Phys. Chem. Lett. 8 (2017) 4679-4684.
[10] E. G. Kelley, P. D. Butler and M. Nagao: in Characterization of Biological Membranes–Structure and Dynamics, Ed. J. Katsaras, M. P. Nieh, F. A. Heberle, de Gruyter, Chap. 4 (2019) 131.
[11] S. A. Shkulipa, W. K. den Otter and W. J. Briels: Biophys. J. 89 (2005) 823-829.
[12] A. Zgorski, R. W. Pastor and E. Lyman: J. Chem. Theory Comput. 15 (2019) 6471-6481.
[13] M. Nagao et al.: Phys. Rev. Lett. 127 (2021) 078102.
[14] F. Mezei, W. Knaak and B. Farago: Phys. Rev. Lett. 58 (1987) 571-574.
[15] J. Wuttke, W. Petry and S. Pouget: J. Chem. Phys. 105 (1996) 5177-5182.
[16] M.S. Green: J. Chem. Phys. 22 (1954) 398-413.
[17] R. Kubo: J. Phys. Soc. Jpn. 12 (1957) 570-586.
[18] T. Yamaguchi: J. Chem. Phys. 146 (2017) 094511.
[19] M. Saito, R. Masuda, Y. Yoda and M. Seto: Sci. Rep. 7 (2017) 12558.
[20] 齋藤真器名、山口毅、長尾道弘：物理学会誌, in press.
[21] F. Mezei: Z. Phys. 255 (1972) 146-160.
[22] 長尾道弘：波紋19 (2009) 42-48.
[23] M. C. Rheinstädter et al.: Phys. Rev. Lett. 101 (2008) 248106.
[24] A. Filippov, G. Orädd and G. Lindblom: Biophys. J. 84 (2003) 3079-3086.
[25] E. Evans and E. Sackmann: J. Fluid Mech. 194 (1988) 553-561.
[26] E. G. Kelley, P. D. Butler, R. Ashkar, R. Bradbury and M. Nagao: Proc. Natl. Acad. Sci. USA 117 (2020) 23365-23373.
[27] A. C. Woodka, P. D. Butler, L. Porcar, B. Farago and M. Nagao: Phys. Rev. Lett. 109 (2012) 058102.
[28] R. Merkel, E. Sackmann and E. Evans: J. Phys. France 50 (1989) 1535-1555.
[29] Y. Wu et al.: Phys. Chem. Chem. Phys. 15 (2013) 14986-14993.
[30] W. K. den Otter and S. A. Shkulipa: Biophys. J. 93 (2007) 423-433.

長尾　道弘　NAGAO Michihiro
Department of Materials Science and Engineering, University of Maryland
College Park, MD 20742-2115, USA
TEL : +1-301-975-5505
e-mail : mnagao@umd.edu