Volume 26, No.2 Pages 142 - 147
2. ビームライン/BEAMLINES
機械学習手法の導入によるデータ解析高度化
Upgrade of Data Analysis Method by using Machine Learning Technique
(公財)高輝度光科学研究センター 放射光利用研究基盤センター 分光推進室 Spectroscopy Division, Center for Synchrotron Radiation Research, JASRI
- Abstract
- 近年、機械学習の技術が急速に発展しており、その技術をサイエンス分野に適用する動きが活発化している。我々はこの技術を用いて、放射光計測データの解析法の高度化を精力的に行ってきた。本稿では、我々の成果である、1.ベイズ統合による異種計測X線分光のハミルトニアンパラメータ推定とその精度推定、2.ベイズ推定を用いた磁気コンプトン散乱測定における測定終了条件設定、の2例を紹介し、今後の展望を述べる。
1. 緒言・背景
今や機械学習の一つである深層学習による自動車の自動運転やデータ同化による天気予報など、我々の生活に密着したところで機械学習の技術が日々活躍している。このような機械学習の手法をサイエンスに適用しようとする動きが近年活発化している。Google DeepMindのDemis HassabisやFacebook AIセンターのYann Le CunらがCERN(欧州原子核機構)において人工知能に関する講演を行っていることもその流れの一つである。我が国においても、物質科学にも関連する領域では新学術領域「スパースモデリングの深化と高次元データ駆動科学の創成」(2013−2017:代表/東京大学 岡田真人教授)[1][1] http://sparse-modeling.jp
代表例: The Astrophysical Journal Letters 875 (2019) L1.や、CREST・さきがけ「計測技術と高度情報処理の融合によるインテリジェント計測・解析手法の開発と応用」(2016−:統括/JASRI 雨宮慶幸理事長)[2][2] https://www.jst.go.jp/kisoken/crest/research_area/ongoing/bunyah28-3.html
代表例: J. Phys. Soc. Jpn. 88 (2019) 024009.あるいは、情報統合型物質・材料開発イニシアティブ(MI2I)(2015−2020:伊藤聡代表)[3][3] https://www.nims.go.jp/MII-I/
代表例: npj Computational Materials 5 (2019) 39.などの大型プロジェクトが続々と立ち上げられ、目覚ましい成果を挙げている[1-3][1] http://sparse-modeling.jp
代表例: The Astrophysical Journal Letters 875 (2019) L1.
[2] https://www.jst.go.jp/kisoken/crest/research_area/ongoing/bunyah28-3.html
代表例: J. Phys. Soc. Jpn. 88 (2019) 024009.
[3] https://www.nims.go.jp/MII-I/
代表例: npj Computational Materials 5 (2019) 39.。
このような背景の下、JASRIにおいて我々のグループは機械学習の導入によるデータ解析の高度化を進めることで成果最大化・測定効率化を目指している。具体的には、機械学習技術であるベイズ推定の導入により、1)間接測定される物理量の統計的精度を評価することによるデータの高付加価値化、2)極端条件下での測定で、必要な精度を得るための実験条件が実験を行う前の事前シミュレーションによる実験の効率化に用いる、3)物理モデルの良し悪しを判定し、モデル選択を行うことでデータから対象としている現象を理解する、さらには新たなモデルを提案しそれをベイズ推定により評価し新しいサイエンスを提唱するなどを行っている。大量のデータからのデータマイニングも機械学習を用いた重要なアプローチであるが、我々は一つひとつのデータを大事にすることで、測定者が一生懸命に測定したデータに存在する情報をでき得る限り抽出することを目的にデータ解析技術の高度化を行ってきた。本稿では、最近挙げた幾つかの成果について以下に紹介する。
2. 導入した機械学習技術
2-1. ベイズ推定を用いたハミルトニアン選択
X線光電子分光(XPS)やX線吸収分光測定(XAS)は、元素・軌道選択性をもった手法で着目する原子の価数や配位子との結合などの電子状態を明らかにする強力な測定手法である。これらXPS・XASスペクトル解析は、従来不純物アンダーソン模型[4][4] F. de Groot and A. Kotani: Core Level Spectroscopy of Solids (CRC Press, Boca Raton, FL, 2008).やクラスター模型[5][5] K. Okada, T. Uozumi and A. Kotani: J. Phys. Soc. Jpn. 63 (1994) 3176-3184.を用いた理論スペクトルと実験スペクトルとを比較し、解析者が一致したかを判断する。この場合、ハミルトニアンに含まれる物理パラメータ(クーロン相互作用、混成相互作用)は点推定となり、精度は決められない。またどのモデルが良いかも解析者の主観によってしまう。XASとXPSの解析を各スペクトルでそれぞれ行い、XPSで決定しやすいパラメータを決めてその後XASでその他のパラメータを決定し、両スペクトルを矛盾なく説明できるパラメータを解析者が決め、両スペクトルを統合的に解析してきた。これも解析者の主観が入ってしまう問題点が存在する。これらの問題点を解決すべく、我々はこれらのスペクトル解析にベイズ的スペクトル分解[6][6] K. Nagata, S. Sugita and M. Okada: Neural Networks 28 (2012) 82-89.を適用して、間接的測定量であるハミルトニアンパラメータ(クーロン相互作用や混成相互作用)を精度付きで評価し、XPS・XAS測定から評価できるハミルトニアンパラメータのベイズ的統合に成功した[7][7] Y. Yokoyama, T. Uozumi, K. Nagata, M. Okada and M. Mizumaki: J. Phys. Soc. Jpn. 90 (2021) 034703.。またベイズ情報量基準に基づいたハミルトニアン選択も可能であることを示した[8][8] Y. Mototake, M. Mizumaki, I. Akai and M. Okada: J. Phys. Soc. Jpn. 88 (2019) 034004.。本稿では、XPS・XASの異種計測ベイズ統合による間接測定量の精度評価の結果について示す。
ベイズの定理は、
| ・・・ (1) |
と書ける。P(θ|D)は事後確率でデータDが取得された下でのパラメータセットθが得られる確率、P(D|θ)はパラメータセットが与えられた時のデータが得られる確率(尤度と呼ばれる)、P(θ)はパラメータの事前確率、P(D)はデータが得られる確率である。
ここで具体的な問題へ適用する前にこの式の意味を考えてみる。尤度P(D|θ)は、我々の測定行為そのもので、データはノイズを含んだ形で得られる。ノイズの確率分布は誤差論に基づきガウス分布が仮定されることが多く、本稿ではガウス分布を採用する。事後確率分布P(θ|D)は本当に我々がデータから抽出したい量で、データを生成するモデルのパラメータの分布を与える。つまりベイズの定理は、データのばらつきが実験の誤差分布ではなくモデルパラメータのばらつきから生じるという発想の転換を意味している。この発想の転換により、間接物理量であるパラメータの値と精度を得ることができるのである。実装するために以下で定式化を行う。データ(実験データ)yiは入力応答関数f(xi; θ)とノイズの足し合わせと考えて、
| yi = f(xi; θ) + ni (i = 1,2,・・・,N) | ・・・ (2) |
と表す。ノイズがガウス分布すると仮定すれば、得られるデータの得られる確率は、
| ・・・ (3) |
と表される。データyiが各iで独立と仮定すれば、データセットY = {y1,・・・,yN}の尤度P(Y|θ)は、
| ・・・ (4) |
ここで、![]() である。この確率分布を得るために交換レプリカモンテカルロ(RXMC)法を用いている。数万回のモンテカルロステップを経て事後確率分布が得られる。RXMCの詳細については参考文献[6]を参照していただきたい。
である。この確率分布を得るために交換レプリカモンテカルロ(RXMC)法を用いている。数万回のモンテカルロステップを経て事後確率分布が得られる。RXMCの詳細については参考文献[6]を参照していただきたい。
我々は、XASおよびXPSのスペクトルを以下の理論モデルにより生成し、ガウスノイズを足し合わせることで実験データを模擬した。ベイズ統合の効果を検討するために、1)それぞれスペクトルに対してベイズ推定を行う、2)2つのスペクトルに対して同時にベイズ推定するベイズ統合を行う、という2つの場合について電子物理量の精度を比較した。その結果を以下に示す。NiOを念頭に置き、正八面体クラスター[NiO6]10-を対象とした。それらのXAS・XPSスペクトルを、XAS・XPSの始状態・終状態を表すハミルトニアンは、
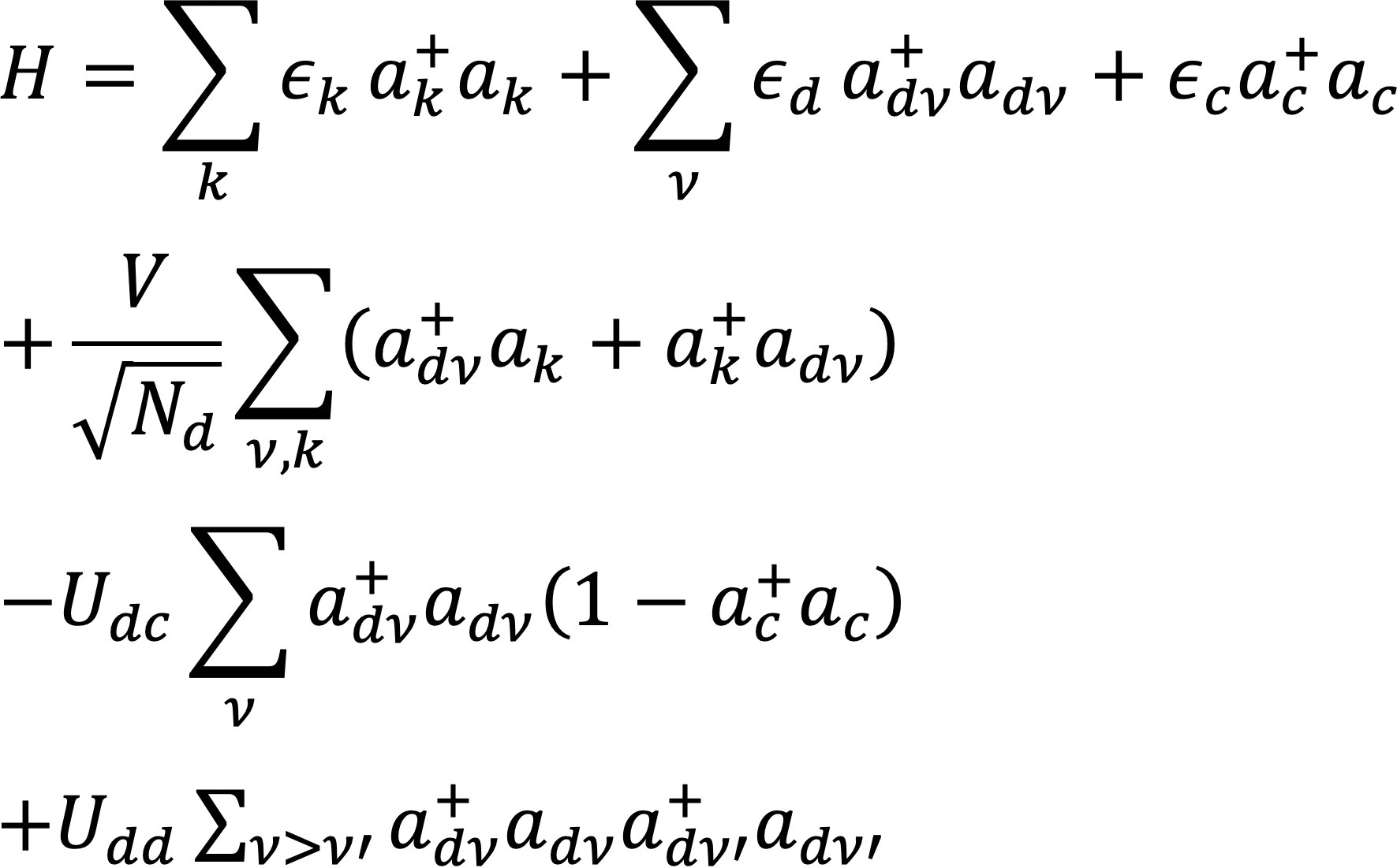 |
・・・ (5) |
で与えられ、XAS・XPSの素過程は、
| ・・・ (6) |
と表される。ϑは、{Δ = ∊k – ∊d, 10Dq, V, Udc, Udd, Γ}である。パラメータはそれぞれ∊kは価電子のエネルギー、∊dはd電子のエネルギー、10Dqは結晶場分裂エネルギー、Vは混成相互作用、Udcは内殻正孔とd電子とのクーロン相互作用、Uddはd電子同士のクーロン斥力である。(5)式から基底状態|g〉と終状態|f〉を求めて(6)式に代入することでXAS・XPSの強度が求まる。Tは、双極子演算子である。Γはピークの幅で内殻正孔の寿命で決まる。
この定式化を用いたNiの2p-XAS、2p-XPSの計算スペクトルは図1のようである。ノイズはXAS・XPSでS/N比が同一になるように設定している。XAS・XPSスペクトルに対して、それぞれベイズ推定を行った。(4)式のEをXASとXPSそれぞれに用意し、
| ・・・ (7) | |
| ・・・ (8) |
と表す。θXAS、θXPSはそれぞれのパラメータで、N(M)はXAS(XPS)の測定点数である。それぞれの事後確率P(Y|θ)を最大となるように推定を行った。その結果、各ハミルトニアンパラメータ(Γ以外を示す)は図2に示すような事後確率分布を示した。これにより間接測定量であるハミルトニアンパラメータの精度が評価できていることが分かる。おおよそXPSの方がパラメータの精度が高い。これはNi2+を対象と選んでいる特殊事情が絡んでいる。詳細は参考文献[7]を読んでいただきたい。次に統合の結果を示す。統合ではEXASとEXPSのデータ点数と測定データの標準偏差で加重平均をとった新たなEtotalを(4)式のEに代入する。このEの変換をすることでベイズ統合が行われる。その結果を図2に示す。別々でベイズ推定を行うよりも統合して行った方が各パラメータの推定精度が高くなっている(分布幅が狭くなっている)ことが図2から見て取れる。またベイズ自由エネルギーを用いたベイズ情報量基準によれば、ベイズ自由エネルギーが低い方がモデル選択される。このことから統合を行った方が良いと結論付けられる(表1)。この結果を鑑みれば、対象とした系の電子状態を正確に理解するには異種の測定を統合して知ることが重要であるということを示唆している。対象の本当の「姿」を見たければ、様々な角度から「見る」ことが重要なのである。
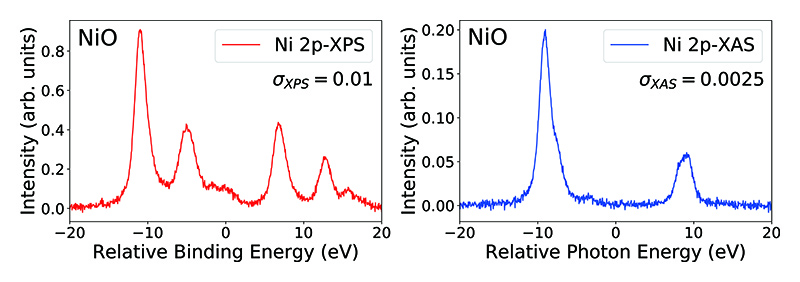
図1 NiOの2p-XPSと2p-XASの人工データ
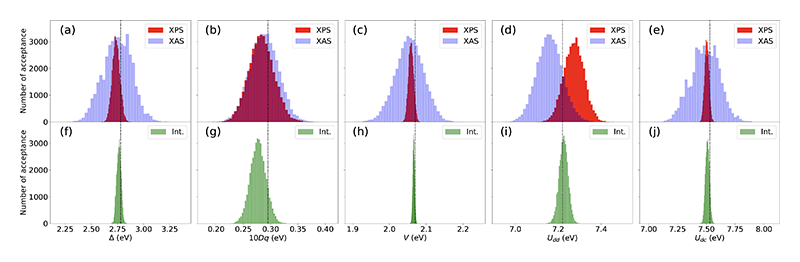
図2 XAS・XPSの各々でのベイズ推定による事後確率分布(上段)と統合後の事後確率分布
表1 ベイズ自由エネルギーの比較:太字の数字を比較する。一番下段が統合の結果。
| ベイズ自由エネルギー | |
| XPS | -2517.6 |
| XAS | -3644.9 |
| XPS+XAS | -6162.5 |
| 統合 | -6180.5 |
2-2. ベイズ推定を用いた実験戦略の提案
次は、実験の目的により、どの程度の時間をかければ良いかをベイズ推定により決定する方法を紹介する。我々はこの方法を磁気コンプトン散乱に適用した。
コンプトン散乱は、固体中の電子の運動量を観測するもので、実空間の波動関数をフーリエ変換した「運動量空間の波動関数」を観測する手法である。入射X線に円偏光を用い、強磁性体のコンプトン散乱を測定すればスピンに依存したコンプトン散乱スペクトルが得られ、スピンの情報をもった電子の波動関数が得られる。このスペクトルを磁気コンプトン散乱スペクトルと呼び、その積分強度はスピン磁気モーメントの大きさを反映したものとなる。スピンに依存した電子運動量分布を測定できること、スピン磁気モーメントが評価できることから強相関電子系の電子状態や磁性材料の特性を調べる強力な手段となっている。特に高エネルギーX線を用いるため、バルクの性質を強く反映すること、試料周りの外場(磁場・高圧・温度など)パラメータを制御しながらの測定が容易であるといった特長をもつ。しかしながら、コンプトン散乱の散乱断面積が非常に小さく測定に非常に時間がかかることが、磁気的性質を調べる他の手段と比べて不利な点である。この問題を解決するために、現在行われている測定終了条件を見直すことを考えた。今回は強磁性体であるFeを対象とした。磁気コンプトン散乱スペクトルは円偏光を入射し、フォトンの波数ベクトルと磁場が平行(+)・反平行(-)という配置のスペクトルの差分を取ることで得られる。実際の測定の際は磁場反転を(+)→(-)→(-)→(+)というサイクルを1サイクルとしてスペクトルとして得ている。以下の2種類の問題設定を用意した。1)磁気コンプトン散乱のスペクトルから3d電子軌道成分と4s電子軌道成分をある精度で分離評価できると測定を終了する。2)Feのスピン磁気モーメントがある精度で評価できると測定を終了する。測定はBL08Wにて室温で行った。Feの磁気コンプトン散乱スペクトルを図3に示す。136サイクルの積算を行った結果である。白丸が実験で、点線、破線がFe-3d、4sの理論スペクトルで、それらの和が実線である。理論スペクトルはFe原子の3d、4sの波動関数をHartree-Fock近似の下で評価したものである。これら2つの理論スペクトルの和を用いて実験スペクトルをフィッティングした結果が実線に対応している。フィッティングの結果、運動量がゼロ付近のスペクトルの凹みは4sが担っており、3d電子のスピン磁気モーメントと4sのそれが反対向きであることが分かる。このスペクトルにベイズ推定を以下のように適用する。測定データyiが先述した(2)式で表されるとすると、f(xi; θ)は理論スペクトルとなるが、それらは3d成分Fe3dと4s成分Fe4sを和で表されるため、
| f(xi; θ) = ([a3dFe3d + a4sFe4s] * G)(xi) | ・・・ (9) |
となる。ここで、![]() であり、*は畳み込み演算子であり、xiは運動量を表す。この幅Γは測定系分解能に対応する。2.2節と同様に各点は独立で、(2)式のノイズがガウスノイズであるとすると、
であり、*は畳み込み演算子であり、xiは運動量を表す。この幅Γは測定系分解能に対応する。2.2節と同様に各点は独立で、(2)式のノイズがガウスノイズであるとすると、
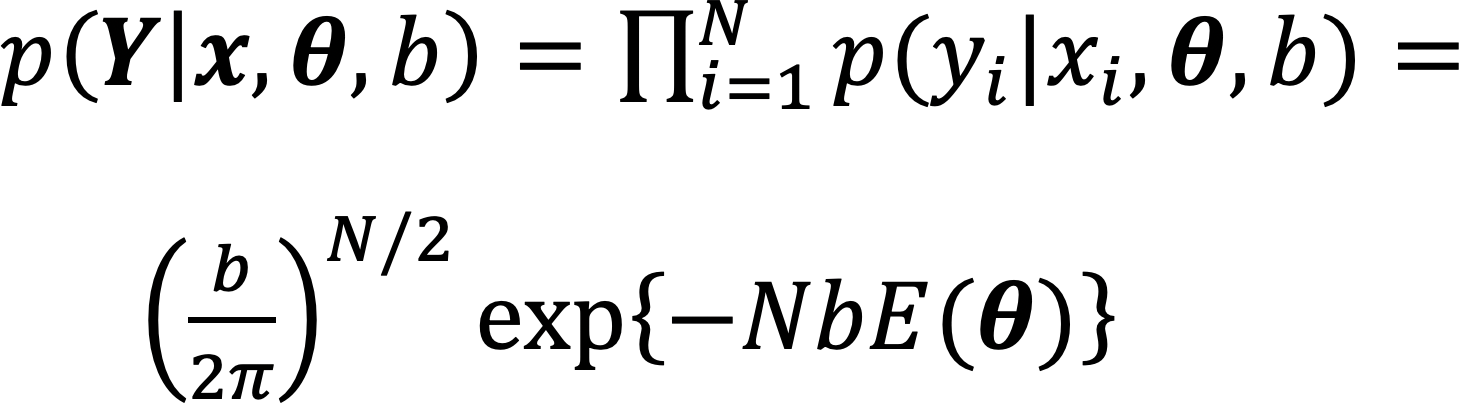 |
・・・ (10) |
ここで、![]() である。
である。
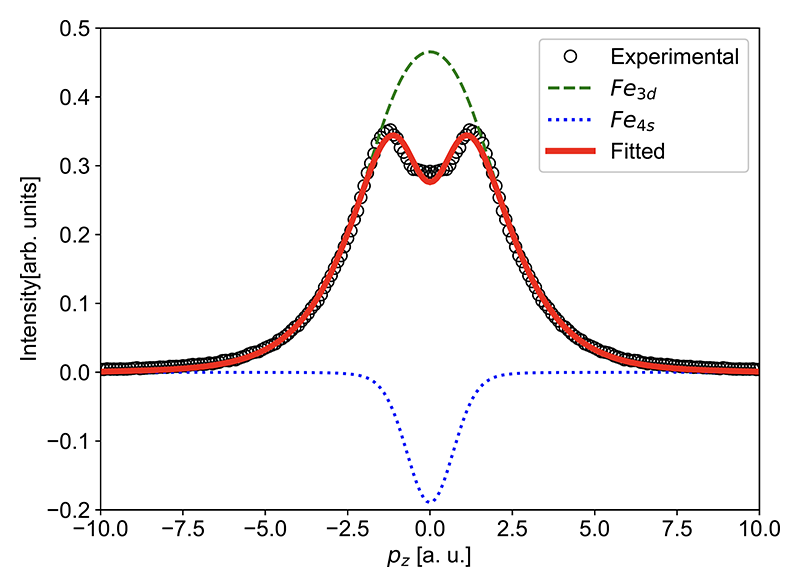
図3 Feの磁気コンプトンスペクトル
この定式化によりベイズ推定を行い、θ = (a3d, a4s, Γ)を精度ともに評価する。これらパラメータをサンプリングし、評価することにより、磁気コンプトンスペクトルの形状・面積(スピン磁気モーメントに対応)といった物理量もサンプリングすることが可能となり、精度付きでの評価が可能となる[9][9] Y. Yokoyama et. al: in preparation.。このベイズ推定を1サイクル分、2サイクル分積算したもの、・・・、136サイクル分積算したもの、それぞれに適用した。まず、1)の結果を示す。図5に3つのパラメータの事後確率分布を示す。これらの分布の標準偏差の積算サイクル依存性と、磁気コンプトン散乱の統計誤差のそれを図4に示す。統計誤差の方は徐々に滑らかに減少し、事後確率分布の標準偏差はおおよそ20サイクル積算したところで最小値を取り、それ以降一定である。この係数の精度がプロファイルの“合い”を表していると考えることができるため、この精度が一定値を示す20サイクルで実験を終了することができる。一方、統計誤差の方はそのような振る舞いがなく、決定しづらいことが見て取れる。従って、事後確率分布の標準偏差を指標にすれば明瞭に収量条件を決定可能となる。次に、2)の結果について示す。図5に磁気コンプトン散乱スペクトルの積分強度の事後確率分布とその標準偏差の積算サイクル依存性を示す。通常磁気コンプトン散乱測定から要求される磁気モーメントの精度は±0.01 μBであり、その範囲を点線で示している。図5を見れば分かるように6サイクル程度積算すれば、事後確率分の標準偏差は要求精度範囲内に収まる。このことから磁気モーメントを評価したいのであれば6サイクル積算で十分ということになる。これは従来の測定時間の20分の1程度となり、大幅な効率化が望める。
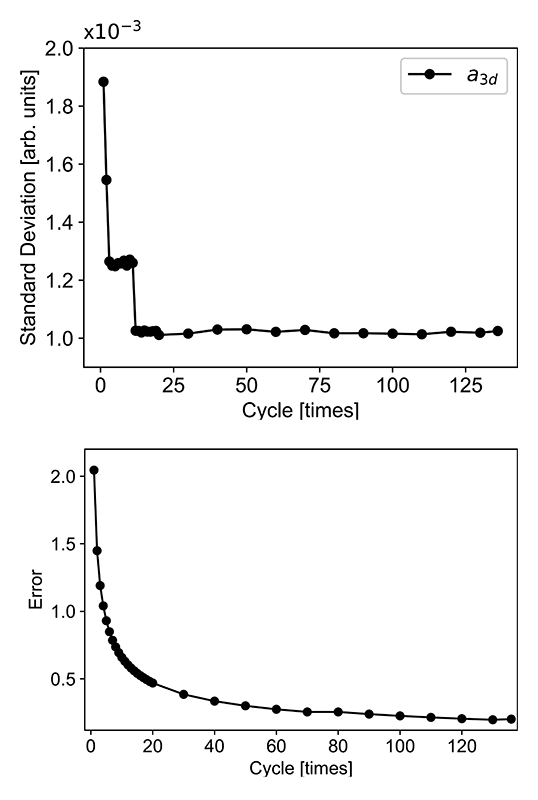
図4 Fe-3d成分の係数の事後確率分布の標準偏差(上段)と磁気散乱強度の統計誤差(下段)。
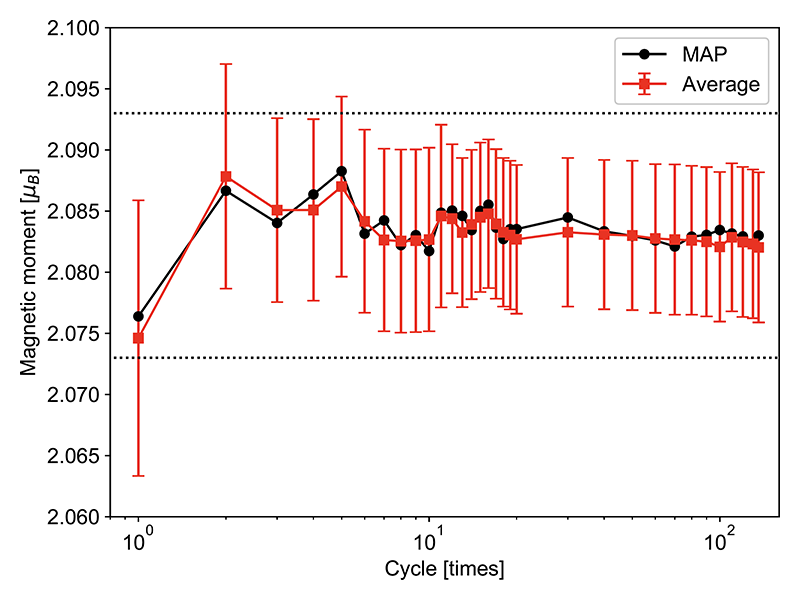
図5 ベイズ推定による磁気モーメントの最尤推定(黒丸)と平均値(赤丸)とその標準偏差(誤差棒)。
2-3. その他の例
我々は、上述したベイズ推定という機械学習技術以外にも導入を始めている。BL40B2において小角散乱測定の自動化に向けた準備として、カーネル密度推定(KDE)法を導入した。散乱パターンにカーネル密度推定法を適用し、散乱パターンの確率密度が収束した時点で測定を終了とする方法を確立した[10][10] H. Sekiguchi et. al: in preparation.。また次世代光源においてさらに進展すると期待される物性研究に対するコヒーレント利用を想定し、磁区パターンのコヒーレント回折イメージングの実像再構成にも取り組んでいる。通常行われている位相回復アルゴリズムを発展させ、スパースモデリングと全変動正則化を導入することで磁区パターンの実像回復が比較的少ない繰り返し回数で可能となっている[11][11] Y. Yokoyama et. al: in preparation.。さらに、これまであまり省みられてこなかった画像データの特徴量の定量化にも取り組んでいる。島状磁区パターンと迷路状磁区パターンの違いの定量化を人間の視覚認知科学の概念に基づいた高次元テキスチャー特徴量であるPortilla-Simoncelli(PSS)特徴量[12][12] J. Portilla and E. P. Simoncelli: Int. J. Comput. Vis. 40 (2000) 49-70.を用いて行った[13][13] R. Murakami, M. Mizumaki, Y. Hamano, I. Akai and H Shouno: J. Phys. Soc. Jpn. 90 (2021) 044705.。これにより、与えられた磁区パターンがどの程度島状であるかを測ることが可能となった。それだけでなく、どの程度島状であるかを示す量は、過飽和度と呼ばれる物理量と比例関係にあることまで分かってきた。詳細は参考文献[13]を読んでいただきたい。
3. まとめ
本稿では、我々が近年行ってきた機械学習の導入によるデータ解析の高度化の進展について紹介した。異種測定のベイズ統合による「データの高付加価値化」、ベイズ推定を用いた「測定の効率化」が機械学習を導入すると可能となることを示した。さらには、近年放射光測定技術の格段の進歩により、重要度が増している画像データの「見た目」の定性的な議論にとどまらず、画像データの定量的議論への道筋を示した。今後は、BL08WやBL40B2に限らず、他のビームラインへも機械学習手法の導入を検討していきたい。
謝辞
本研究は多くの方々にお世話になりました。ここに感謝申し上げます。1つ目の例は、JASRI 博士研究員の横山優一博士が精力的に進めてくれました。2つ目の例は、BL08W担当者の辻成希博士の協力なくしてはできませんでした。お礼申し上げます。BL40B2の測定・KDE法導入では、JASRI 関口博史博士、太田昇博士に大変お世話になりました。また、ベイズ推定の方法論や情報数理科学の議論においては、東京大学新領域 岡田真人教授、熊本大学 赤井一郎教授、NIMS 永田賢二主任研究員、統計数理研究所 日野英逸教授、福水健次教授、本武陽一助教に、磁区パターンの解析においては、電気通信大学 庄野逸教授、修士1年の村上諒君には大変お世話になりました。XAS・XPSスペクトル計算の理論に関する議論は、大阪府立大学 魚住孝幸教授にアドバイスをいただきました。心より感謝申し上げます。また、本研究はJST-CREST(JPMJCR1761、JPMJCR1861)の助成により行いました。
参考文献
[1] http://sparse-modeling.jp
代表例: The Astrophysical Journal Letters 875 (2019) L1.
[2] https://www.jst.go.jp/kisoken/crest/research_area/ongoing/bunyah28-3.html
代表例: J. Phys. Soc. Jpn. 88 (2019) 024009.
[3] https://www.nims.go.jp/MII-I/
代表例: npj Computational Materials 5 (2019) 39.
[4] F. de Groot and A. Kotani: Core Level Spectroscopy of Solids (CRC Press, Boca Raton, FL, 2008).
[5] K. Okada, T. Uozumi and A. Kotani: J. Phys. Soc. Jpn. 63 (1994) 3176-3184.
[6] K. Nagata, S. Sugita and M. Okada: Neural Networks 28 (2012) 82-89.
[7] Y. Yokoyama, T. Uozumi, K. Nagata, M. Okada and M. Mizumaki: J. Phys. Soc. Jpn. 90 (2021) 034703.
[8] Y. Mototake, M. Mizumaki, I. Akai and M. Okada: J. Phys. Soc. Jpn. 88 (2019) 034004.
[9] Y. Yokoyama et. al: in preparation.
[10] H. Sekiguchi et. al: in preparation.
[11] Y. Yokoyama et. al: in preparation.
[12] J. Portilla and E. P. Simoncelli: Int. J. Comput. Vis. 40 (2000) 49-70.
[13] R. Murakami, M. Mizumaki, Y. Hamano, I. Akai and H Shouno: J. Phys. Soc. Jpn. 90 (2021) 044705.
(公財)高輝度光科学研究センター
放射光利用研究基盤センター 分光推進室
〒679-5198 兵庫県佐用郡佐用町光都1-1-1
TEL : 0791-58-0833
e-mail : mizumaki@spring8.or.jp








