Volume 24, No.4 Pages 371 - 375

1. 序論
　磁気光学効果とは、磁性体の磁化が光の偏光状態を変化させる現象であり、光をプローブとした磁性測定に19世紀より広く利用されてきた。代表的なものにファラデー効果や磁気光学カー効果（magneto-optical Kerr effect, MOKE）がある^[1,2][1] 佐藤勝昭：光と磁気 改訂版（朝倉書店、2001）
[2] P. M. Oppeneer: Handbook of Magnetic Materials 13 (Elsevier, Amsterdam, 2001).。磁気光学効果では、磁性体による左右の円偏光の吸収の差に由来する磁気円二色性（MCD）と左右の円偏光の位相差の変化に由来する磁気旋光性から磁性情報が得られる。ここで、本稿で用いるMOKEを例に見てみる。MOKE測定では直線偏光の光を磁性体に照射し、その反射光の偏光状態変化を測定する。まず、MCDにより直線偏光は楕円偏光に変化する。次に、磁気旋光性により、偏光面が回転する。この回転角をカー回転角と言い、楕円偏光の楕円率との2つのパラメータでMOKEは記述でき、磁性情報を得ることができる。これらのパラメータを同時測定する方法として、偏光が連続的に変調する可視光レーザーを使った光学遅延変調法がある^[1,3,4][1] 佐藤勝昭：光と磁気 改訂版（朝倉書店、2001）
[3] K. Sato: Jpn. J. Appl. Phys. 20 (1981) 2403-2409.
[4] K. Sato, H. Kida and T. Kamimura: J. Magn. Soc. Jpn. 11 (1987) 113-116.。
　一方、入射する光の波長を、磁性体を構成する元素の吸収端に合わせることで、元素選択的な測定ができるとともに、共鳴効果により大きな信号が得られる。代表的な3d磁性元素のL殻吸収端をカバーする軟X線領域では、2つの磁気光学パラメータのうち、MCDのみを用いたX線MCD（XMCD）測定が有用な磁性測定手法として広く用いられてきた^[5][5] C. T. Chen et al.: Phys. Rev. Lett. 75 (1995) 152.。さらに最近では、MOKE測定においても軟X線領域の吸収端を利用した研究が進められており（特に共鳴MOKEと呼ぶ）、可視光を用いるよりも大きなカー回転角（磁気旋光性）の測定が可能となっている^[6-10][6] J. B. Kortright and S.-K. Kim: Phys. Rev. B 62 (2000) 12216.
[7] H.-C. Mertins et al.: Phys. Rev. B 69 (2004) 064407.
[8] S. Valencia et al.: Phys. B Condensed Matter 345 (2004) 189-192.
[9] J. B. Kortright: J. Electron Spectrosc. Relat. Phenom. 189 (2013) 178.
[10] M. F. Tesch et al.: Appl. Opt. 52 (2013) 4294-4310.。主に全電子収量法を用いるXMCD測定と比較して、photon-in photon-outの測定である共鳴MOKE測定はバルク敏感であり、埋込磁性層や界面磁性などの測定に有用である。しかし、XMCD測定ではMCDのみ、共鳴MOKE測定では磁気旋光性のみの情報しか観測が難しく、軟X線領域の磁性情報の完全な測定は実現していなかった。これは、この波長領域において偏光を連続的に変調させる方法が存在しなかったからである。
　そこで、本研究では、SPring-8 BL07LSU^[11][11] S. Yamamoto et al.: J. Synchrotron Radiat. 21 (2014) 352-365.における分割型クロスアンジュレータの特性を活かして世界初の連続型偏光変調軟X線（以下、変調軟X線とする）光源を開発し、それを用いたMCDと磁気旋光性の同時測定を実現した。2つの磁気光学パラメータを測定できたことで、物質の基本的な固有パラメータである複素誘電率テンソルを完全決定できる^[2,12,13][2] P. M. Oppeneer: Handbook of Magnetic Materials 13 (Elsevier, Amsterdam, 2001).
[12] L. L. Landau and E. M. Lifshitz: Electrodynamics of Continuous Media 8 (Pergamon, Elmsford, NY, 1960).
[13] B. Donovan and T. Medcalf: Proc. Phys. Soc. 86 (1965) 1179.。軟X線領域で初めて得られた複素誘電率テンソルの非対角項スペクトルも示す。

2. 実験手法
　変調軟X線光源はSPring-8 BL07LSU^[11][11] S. Yamamoto et al.: J. Synchrotron Radiat. 21 (2014) 352-365.にて開発した。このビームラインでは、世界唯一の分割型クロスアンジュレータを有している。分割型クロスアンジュレータは、水平方向の直線偏光を発生する水平8の字アンジュレータと垂直方向の直線偏光を発生する垂直8（∞）の字アンジュレータの2種類のアンジュレータから成る。各4台のアンジュレータが交互に並び、その間に移相器が7台設置されている。移相器は永久磁石と電磁石から成り^[14][14] I. Matsuda et al.: Nucl. Instrum. Methods Phys. Res. 767 (2014) 296-299.、電子ビームの軌道を変えることで、水平と垂直の直線偏光間の位相差を制御し、様々な偏光状態の高輝度軟X線の発生が可能である。連続的な偏光変調を実現するためには、この電磁石移相器に交流電流を加えてやれば良い。図1に変調軟X線のイメージを示す。周波数νの正弦波交流電流を電磁石移相器に印加することで、図1(b)に示すような、斜め直線偏光から左右の円偏光へ周波数νで切り替わる変調光源が実現できる。この時の光学遅延量は、

　　　･･･ (1)

で与えられる。ここで、δ₀は遅延量の振幅を表し、直線から右または左円偏光へ連続的に変化する際はδ₀ = π/2となる。この変調光源をMOKE測定に利用すると、磁性体からの反射光強度のうち、MCDに由来する楕円率の情報がν成分として、磁気旋光性に由来するカー回転角が2ν成分として得られる（図1(c), (d)）。つまり、検出信号からν、2ν成分を抽出することで、2つの磁気光学パラメータを同時にかつ高感度に測定することが可能である^[1,3][1] 佐藤勝昭：光と磁気 改訂版（朝倉書店、2001）
[3] K. Sato: Jpn. J. Appl. Phys. 20 (1981) 2403-2409.。

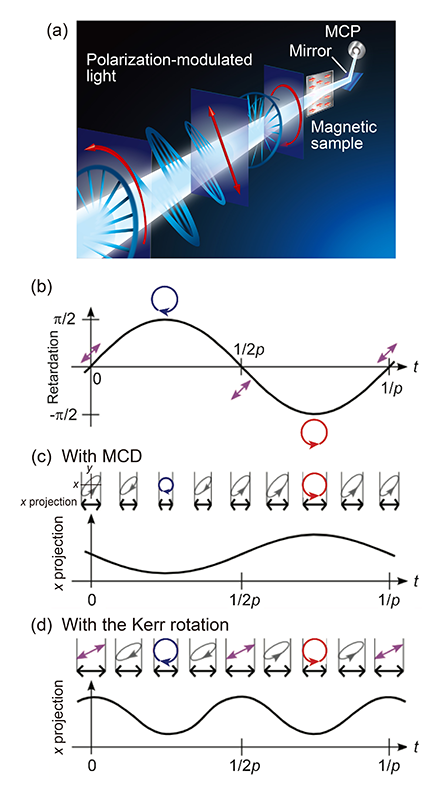
図1　(a) 変調軟X線光源のイメージ図。本研究で用いたL-MOKEの測定配置とともに示す。(b) 光学遅延量δ = (π/2)sin2πνtの時間変化とそれに対応する偏光の変化。斜め直線偏光（skew linearly, SL）→右円偏光→SL→左円偏光→SLと連続的に変化する。(c),(d) MCDと磁気旋光性（カー回転角）がν、2ν成分からそれぞれ得られることの説明図。磁性試料からの反射光電場のx軸方向への投影を(c)MCDを示す場合、(d)磁気旋光性を示す場合に対して図示している（文献17のFig.1からの転載）。

　次に、この変調軟X線を用いた共鳴MOKE測定の具体的な手法を紹介する。今回は図2(a)のように磁化方向が光の反射面に平行な、縦MOKE（longitudinal MOKE, L-MOKE）配置を用いる。従来の軟X線領域の共鳴MOKEでは、カー回転角の測定のためにrotating analyzer ellipsometry（RAE）と呼ばれる手法が用いられてきた。これは、図2に示すように、磁性体からの反射光を多層膜ミラーと検出器から成るユニットに導き、磁性体とミラーを結んだ直線を回転軸として、ユニット全体を回転させる。その回転角をχと定義する。多層膜ミラーからの反射光強度はs偏光配置になった角度χで最大になるので、強度のχ依存性を測定することで、偏光面方向が特定でき、カー回転角を求めることができる。詳細は先行研究[15,16]を参照していただきたい。一方、変調軟X線を入射光として用いると、このχの回転が不要になる。今、図2(a)に示したように、RAEユニットを反射面に対して平行方向（z方向）に固定する場合を考える（χ = π/2と定義する）。この状態で検出器から得られる信号のうち、DC成分、ν成分、2ν成分をそれぞれI(0)、I(ν)、I(2ν)とすると、従来のMOKE測定でs偏光を入射したことに相当するカー回転角と楕円率、θ_K^sとε_K^sが、

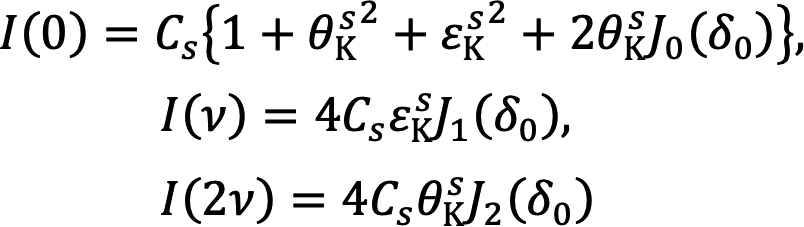　　　･･･ (2)

と表せられる。ここでC_sは比例定数、J_n(δ₀)はn次のベッセル関数をそれぞれ表す。一方、RAEユニットを図2(b)のように反射面に対して垂直方向（x方向）に固定した場合（χ = 0）は、従来手法のp偏光を入射したことに相当するカー回転角と楕円率、θ_K^pとε_K^pが、

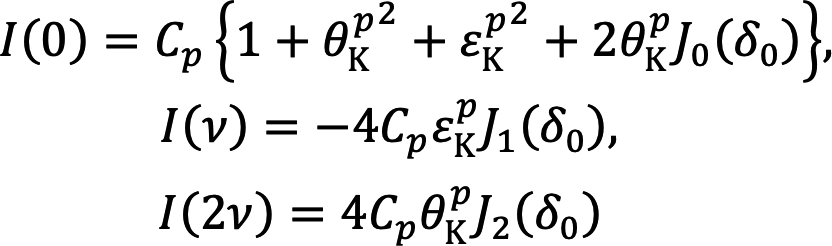　　　･･･ (3)

という式から得られる。ここでC_Pはp偏光に対する比例定数である。式(2)と(3)の詳細に関しては原著論文[17]を参照していただきたい。本研究では、式(1)における偏光変調は交流電流25 ± 0.588 Aを周波数ν = 12.987 Hzで印加して実現させた。交流電流の振幅0.588 Aがδ₀ = π/2に対応し、左右の円偏光を作る。

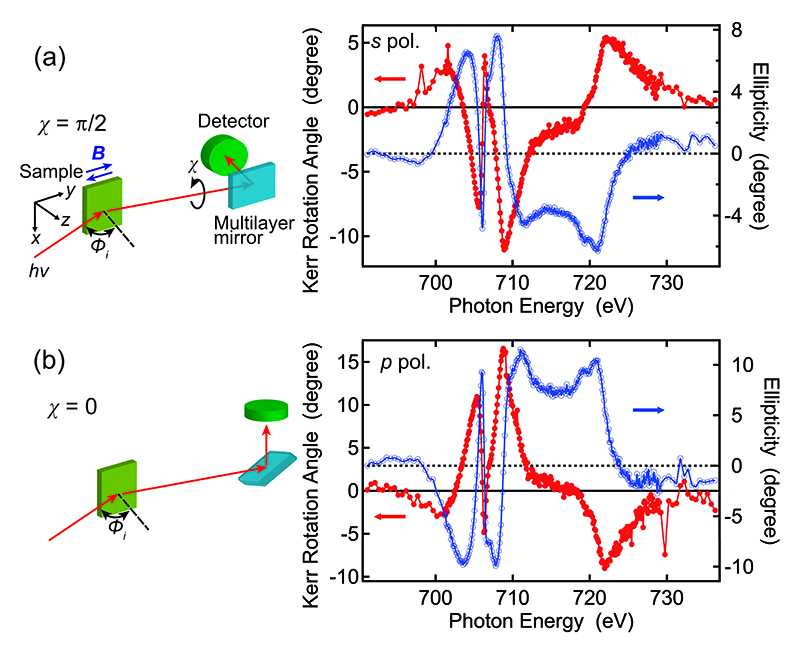
図2　埋込Fe薄膜に対して行った、L殻吸収端における変調軟X線L-MOKE測定結果。(a) s偏光、(b) p偏光入射に対応する場合をそれぞれ示し、その際のセットアップを左図に示している。測定結果の赤丸と青丸はカー回転角（左軸）と楕円率（右軸）のスペクトルをそれぞれ表す（文献17のFig.2を修正して掲載）。

　本研究では測定試料として、マグネトロンスパッタ法で作成した、Ta/Cu/Fe/MgO(001)ヘテロ構造試料を用いた。Ta、Cu、Feの厚みはそれぞれ2、2、30 nmであり、Ta/CuはFeの酸化を防ぐためのキャップ層である。この埋込Fe薄膜は面内に容易磁化方向を持ち、図2(a)に示すy軸方向に飽和磁場以上のB = ± 0.3 Tの外部磁場を超伝導マグネットで印加した。変調軟X線の入射角φ_iはyz平面内で試料の面直方向から約80°とした。試料温度は室温である。

3. 結果と考察
　変調軟X線を用いたFe L殻吸収端におけるL-MOKE測定結果を図3に示す。s偏光、p偏光を入射したことに相当するカー回転角と楕円率のスペクトルがそれぞれ得られた。絶対値は実際の光の偏光度を考慮して較正している。L₃、L₂殻吸収端近傍に構造が見られ、カー回転角スペクトルは従来手法で測定した先行研究結果を再現している^[16][16] Y. Kubota et al.: Phys. Rev. B 96 (2017) 134432.。さらに、新しい測定手法では、RAEユニットを回転する必要がなくなったため、測定時間の大幅短縮につながり、より詳細なスペクトル構造がより短い時間で得られた。また、カー回転角と楕円率はクラマース−クローニヒの関係で結ばれており、それを反映した、お互いの微分形のスペクトルを示していることが見て取れる^[2,18][2] P. M. Oppeneer: Handbook of Magnetic Materials 13 (Elsevier, Amsterdam, 2001).
[18] J. Kunes et al.: Phys. Rev. B 64 (2001) 174417.。ここで、s偏光、p偏光を入射した時のL-MOKEは以下の式で表現される^[2][2] P. M. Oppeneer: Handbook of Magnetic Materials 13 (Elsevier, Amsterdam, 2001).。

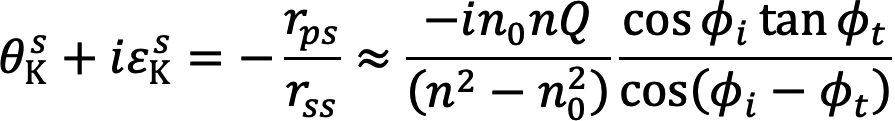　　　･･･ (4)

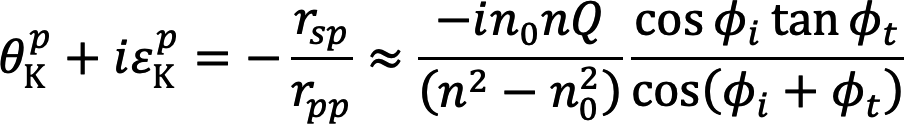　　　･･･ (5)

式中の、複素フレネル係数r_ijは入射光のj偏光電場と反射光のi偏光電場の比率である。また、nとn₀はそれぞれ磁性Fe薄膜とキャップ層（Ta/Cu）の複素屈折率であり、φ_tは屈折角を表す。今回のようにφ_iが大きく（70° ≤ φ_i ≤ 90°）、φ_i ≈ φ_tと近似できる時、分母の余弦関数によりs偏光入射とp偏光入射でカー回転角と楕円率の符号が反転する^[8,15,16][8] S. Valencia et al.: Phys. B Condensed Matter 345 (2004) 189-192.
[15] Y. Kubota et al.: J. Electron Spectrosc. Relat. Phenom. 220 (2017) 17-20.
[16] Y. Kubota et al.: Phys. Rev. B 96 (2017) 134432.。図2を見ると、確かにそのような振る舞いをしているのがわかる。磁気光学の情報は、式(4)と(5)内に現れているフォークトパラメータQに含まれる。このQは物質の基本的な固有パラメータである複素誘電率テンソルの2成分の比で表すことができる。

　　　･･･ (6)

ここで、磁場をy方向に印加した（L-MOKE）時の誘電率テンソルは、

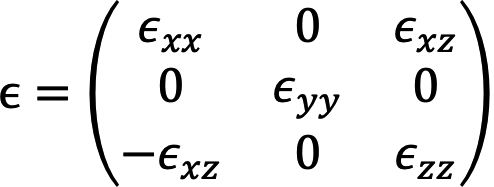　　　･･･ (7)

と表せられる。対角成分ϵ_xxは磁性情報を持たず、ϵ_xx = n²で与えられる。それに対して、非対角成分ϵ_xzが磁気光学特性を表し、磁性を議論する上で重要な物理量となる。式(4)–(6)から、測定条件φ_iとφ_t、磁性に依存しないnとn₀の値がわかれば、カー回転角と楕円率からϵ_xzを求めることができる^[19,20][19] H.-C. Mertins et al.: J. Magn. Magn. Mater. 240 (2002) 451-453.
[20] L. Henke, E. Gullikson and J. C. Davis: http://henke.lbl.gov/optical_constants/。図3に本研究で得られたカー回転角と楕円率の結果から求めたϵ_xzのスペクトルを実部虚部ともに示す。ϵ_xzの実部、虚部の間にもクラマース−クローニヒの関係が成り立つため、スペクトルがそれを反映した微分の関係になっていることがわかる。さらに、第一原理計算で求めたϵ_xzのスペクトルと比較を行った。この計算では、KKR-CPA-LDAパッケージのMachikaneyama（AkaiKKR）を使用し、バルクのFe(bcc)に対するϵ_xzスペクトルをKKRグリーン関数法から計算した^[21][21] H. Akai: http://kkr.issp.u-tokyo.ac.jp。電子構造は密度関数理論の局所密度近似（local-density approximation, LDA）の枠組みで求め、相対論的効果は内殻電子及び価電子ともに考慮している。計算手法の詳細は先行研究を参照していただきたい^[22][22] H. Akai: J. Phys: Condens. Matter 1 (1989) 8045.。その計算結果を図3(b)に示す。スペクトルの絶対値、形状ともに実験値と良い一致を示しているのがわかる。つまり、本研究で新たに開発した測定手法と、本計算手法が、物質の最も基本的なパラメータである複素誘電率テンソルを軟X線領域で求めるのに大変有用であると言える。実験値では706 eV辺りでϵ_xzの実部のピークと、虚部のディップが確認できる。これは、先行研究から薄膜における干渉効果であると言われており^[7,8,16][7] H.-C. Mertins et al.: Phys. Rev. B 69 (2004) 064407.
[8] S. Valencia et al.: Phys. B Condensed Matter 345 (2004) 189-192.
[16] Y. Kubota et al.: Phys. Rev. B 96 (2017) 134432.、バルクに対する計算スペクトルで見られないことからも、試料の形状に由来するスペクトル構造であると考えられる。その詳細は今後他の厚みの試料も測定することで明らかにしていきたい。

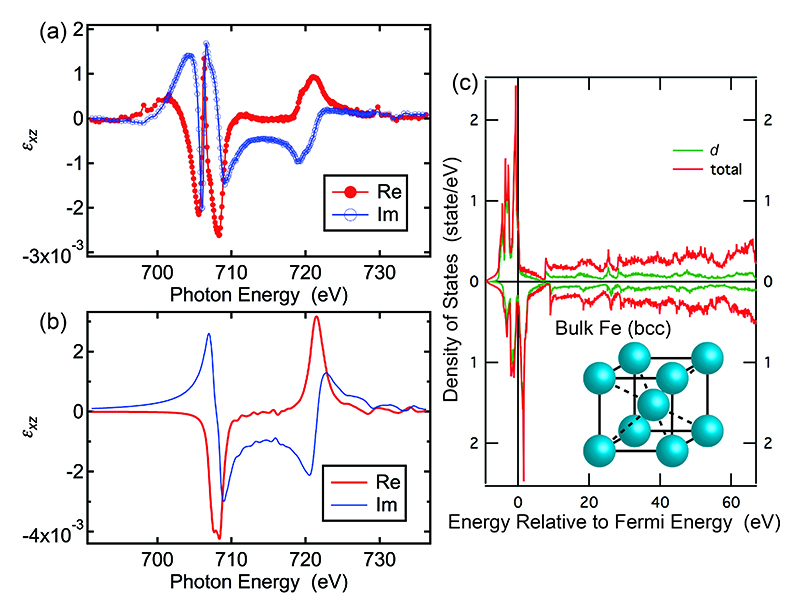
図3　(a) 埋込Fe薄膜のL殻吸収端におけるϵ_xzスペクトル。赤丸と青丸はϵ_xzの実部と虚部をそれぞれ表す。(b) 第一原理計算により得られたバルクFe(bcc)のL殻吸収端におけるϵ_xzスペクトル。赤線と青線はϵ_xzの実部と虚部をそれぞれ表す。(c) 第一原理計算から得られたバルクFe(bcc)の状態密度。赤線と緑線は全状態の状態密度とd電子状態の状態密度をそれぞれ表している。図の上半分がmajorityスピン、下半分がminorityスピンの状態密度である。バルクFe(bcc)の結晶構造を挿入図にて表す（文献17のFig.3からの転載）。

4. 結論
　本研究において、SPring-8 BL07LSUの分割型クロスアンジュレータの特性を十分に活かし、偏光が連続的に変調する軟X線光源を世界で初めて開発した。そして、その光を使って、光学遅延変調法を使った共鳴MOKE測定を埋込Fe薄膜に対して実施し、L殻吸収端におけるカー回転角と楕円率の両スペクトルが得られた。磁気光学効果の2つのパラメータである、MCDと磁気旋光性が同時測定できたことで、物質の基本パラメータである誘電率テンソルを求め、第一原理計算とも良い一致を示すことができた。本研究で新たに開発した磁性測定手法は、1）軟X線を用いることで元素選択性を持つ、2）photon-in photon-outのバルク敏感な測定である、3）特定の周波数を抽出することで高感度に磁性測定ができる、そして、4）誘電率テンソルが決定できる、という特長を持っている。特に、4）の誘電率を求められるということは、物質中の電子構造や光学遷移を軟X線のエネルギースケールで考察できるようになる。さらに、光学素子を設計する上でも有用な情報を与え、高次高調波レーザーや放射光技術の発展に大いに貢献できると期待している。

謝辞
　本稿で紹介した研究結果は、松田巌氏、赤井久純氏、田中隆次氏、辛埴氏、原田慈久氏、和達大樹氏、角田匡清氏、平田靖透氏、田口宗孝氏、宮脇淳氏、山本達氏、保原麗氏、藤澤正美氏、山本真吾氏、山本航平氏、染谷隆史氏、田久保耕氏、横山優一氏、荒木実穂子氏、金城良太氏、鏡畑暁裕氏、清家隆光氏、竹内政雄氏、小嗣真人氏、大門寛氏、成田尚司氏、高橋良暢氏らを始めとする多くの研究者との共同研究や有益な議論に寄っている。この場をお借りして感謝申し上げる。また、本研究は文科省の「X線自由電子レーザー重点戦略研究課題」と「光・量子融合連携研究開発プログラム」にて実施された。また、光科学技術研究振興財団、ひょうご科学技術協会、科学技術振興機構の科学研究費基盤研究（C）（科研費番号：26400328）、東京大学フォトンサイエンス・リーディング大学院（ALPS）より助成を受けた。実験は東京大学放射光分野融合国際卓越拠点及び東京大学物性研究所の共同利用（SPring-8の課題番号：2014A7401、2014B7401、2014B7473、2015A7401、2015B7401、2016A7403、2016A7504、2016B7403）にて行われた。

参考文献
[1] 佐藤勝昭：光と磁気 改訂版（朝倉書店、2001）
[2] P. M. Oppeneer: Handbook of Magnetic Materials 13 (Elsevier, Amsterdam, 2001).
[3] K. Sato: Jpn. J. Appl. Phys. 20 (1981) 2403-2409.
[4] K. Sato, H. Kida and T. Kamimura: J. Magn. Soc. Jpn. 11 (1987) 113-116.
[5] C. T. Chen et al.: Phys. Rev. Lett. 75 (1995) 152.
[6] J. B. Kortright and S.-K. Kim: Phys. Rev. B 62 (2000) 12216.
[7] H.-C. Mertins et al.: Phys. Rev. B 69 (2004) 064407.
[8] S. Valencia et al.: Phys. B Condensed Matter 345 (2004) 189-192.
[9] J. B. Kortright: J. Electron Spectrosc. Relat. Phenom. 189 (2013) 178.
[10] M. F. Tesch et al.: Appl. Opt. 52 (2013) 4294-4310.
[11] S. Yamamoto et al.: J. Synchrotron Radiat. 21 (2014) 352-365.
[12] L. L. Landau and E. M. Lifshitz: Electrodynamics of Continuous Media 8 (Pergamon, Elmsford, NY, 1960).
[13] B. Donovan and T. Medcalf: Proc. Phys. Soc. 86 (1965) 1179.
[14] I. Matsuda et al.: Nucl. Instrum. Methods Phys. Res. 767 (2014) 296-299.
[15] Y. Kubota et al.: J. Electron Spectrosc. Relat. Phenom. 220 (2017) 17-20.
[16] Y. Kubota et al.: Phys. Rev. B 96 (2017) 134432.
[17] Y. Kubota et al.: Phys. Rev. B 96 (2017) 214417.
[18] J. Kunes et al.: Phys. Rev. B 64 (2001) 174417.
[19] H.-C. Mertins et al.: J. Magn. Magn. Mater. 240 (2002) 451-453.
[20] L. Henke, E. Gullikson and J. C. Davis: http://henke.lbl.gov/optical_constants/
[21] H. Akai: http://kkr.issp.u-tokyo.ac.jp
[22] H. Akai: J. Phys: Condens. Matter 1 (1989) 8045.

久保田　雄也　KUBOTA Yuya
（公財）高輝度光科学研究センター　XFEL利用研究推進室
〒679-5198　兵庫県佐用郡佐用町光都1-1-1
TEL : 0791-58-0992
e-mail : kubota@spring8.or.jp