Volume 23, No.4 Pages 316 - 320

1. はじめに
　電磁場のコヒーレンスという概念は、時空における電磁場の振動の位相の相関の度合いを表現する^[1][1] 菊田惺志：X線散乱と放射光科学 基礎編（東京大学出版会、2011）。いわゆるMössbauer効果が起きた場合、励起原子核から弾性的に放射されるガンマ線の電場の位相の相関は、10⁻⁹から10⁻⁵秒の時間に渡って継続する^[2][2] G. V. Smirnov: Hyperfine Interactions 123/124 (1999) 31.。このような位相相関の継続時間をコヒーレント時間または可干渉時間と呼ぶ。放射光X線のコヒーレント時間は、複数の単結晶を用いて分光しても10⁻¹²秒程度に留まることを考えると^[3][3] M. Yabashi, K. Tamasaku, S. Kikuta, T. Ishikawa: Rev. Sci. Instrum. 72 (2001) 4080.、硬X線領域の光としてはMössbauerガンマ線は非常に高い時間コヒーレンスを有するといえる。最も典型的なMössbauer核種である⁵⁷Fe励起核からの14.4 keVガンマ線の場合、互いに位相の相関がある光子の波連の進行方向への長さ（コヒーレンス長）は40 m以上に及ぶものとなる。
　この高い時間コヒーレンスは、Wiener−Khintchineの定理によりMössbauerガンマ線の高い単色性と強く結びついている^[1][1] 菊田惺志：X線散乱と放射光科学 基礎編（東京大学出版会、2011）。この定理によれば、一般に光のエネルギースペクトルのFourier変換より得られる時間スペクトルは、電場の位相の時間相関関数を表す。ガンマ線のエネルギースペクトルの半値全幅がΓ₀とかけるとき、コヒーレンス時間τ₀はτ₀～h/Γ₀と評価できる。すなわちガンマ線のスペクトルの幅が狭いほど、コヒーレンス時間が長いことを示している。⁵⁷Fe励起核からの14.4 keVガンマ線のコヒーレンス時間～10⁻⁷秒は、Γ₀がneVのオーダーであり、ガンマ線のエネルギーに対して13桁も狭いためにもたらされることが確認できる。この高い時間コヒーレンス特性は、これまでMössbauer核を含む物質の物性研究などに有効に用いられてきた^[4,5][4] 瀬戸誠：日本結晶学会誌 43 (2001) 405.
[5] 瀬戸誠：固体物理 44 (2009) 27.。
　本稿で解説する時間領域干渉計を用いた準弾性散乱法は、高い時間コヒーレンスを有する単色ガンマ線をMössbauer核を含まない一般の物質のダイナミクス研究に用いる手法である^[6,7][6] 齋藤真器名：SPring-8/SACLA利用者情報 22 (2017) 91.
[7] 齋藤真器名：固体物理 47 (2012) 11.。2章では、まず実験セットアップや各種実験条件を整理した上で、入射放射光とガンマ線の経路を時空ダイヤグラム上で表現し、基本的なシングルライン条件の場合に得られるガンマ線の時間スペクトルの干渉パターンが、試料中のダイナミクスを反映して時間的に変化する描像を解説する。3章では、マルチラインの時間領域干渉計の概要とその高効率の起源を概説する。4章では、入射放射光のエネルギー幅のガンマ線時間スペクトルへの影響を時間領域上で解説する。5章では、まとめと今後の展望を示す。

2. シングルライン時間領域干渉計の時空ダイヤグラム描像
　以降の議論は一般的なMössbauerガンマ線を用いた時間領域干渉計にも成立するものであるが、ここでは具体的にわかりやすく解説するため、⁵⁷Fe核から放射されるガンマ線を用いた実験を考える。図1に実験セットアップの一例と諸条件をまとめる^[8-10][8] A. Q. R. Baron et. al.: Phys. Rev. Lett. 79 (1997) 2823.
[9] G. V. Smirnov, V. G. Kohn, and W. Petry: Phys. Rev. B 63 (2001) 144303.
[10] G. V. Smirnov, et. al.: Phys. Rev. B 73 (2006) 184126.。

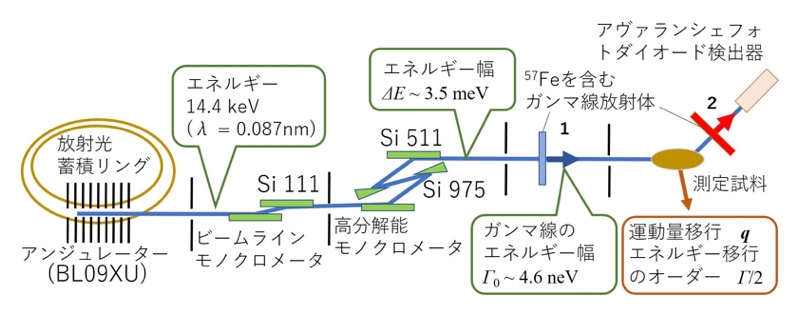
図1　実験セットアップの概念図

　時間領域干渉計システムへの入射放射光は、試料への放射ダメージを軽減するために可能な限り分光しておくことが望ましい。そのため、Nested型の高分解能モノクロメーターを用いることで、エネルギー幅ΔE～meVのオーダーに入射放射光を分光する^[11][11] T. Ishikawa, Y. Yoda, K. Izumi, C. K. Suzuki, X. W. Zhang, M. Ando, and S. Kikuta: Rev. Sci. Instrum. 63 (1992) 1015.。図2(a)左図に、入射光のエネルギースペクトルの模式図を示す。エネルギースペクトルをフーリエ変換により得られる時間スペクトル（図2(a)右図）は、ΔT～h/ΔE程度の時間スケールまでX線電場が干渉性を有することを示している。

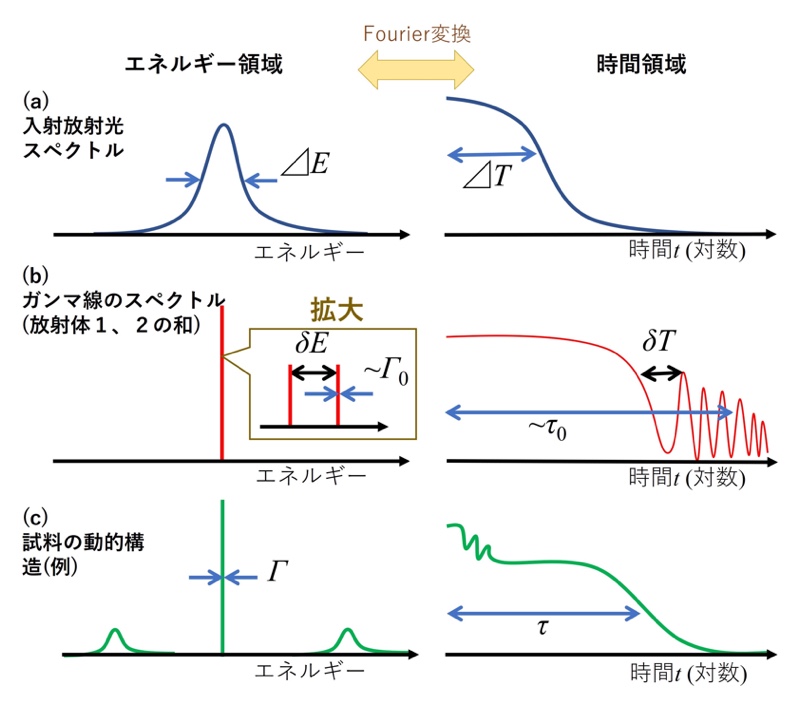
図2　(a) 典型的な入射放射光、(b) ガンマ線の時間スペクトル・エネルギースペクトル（ガンマ線1、2の和）と、(c) 試料の動的構造因子・中間散乱関数の一例

　図2(b)に放射体1および2から放射される全ガンマ線のエネルギースペクトル、時間スペクトルをそれぞれ示す。ガンマ線放射体1、2ではある単一のエネルギーでそれぞれ核励起を起こすものとする。両放射体の違いは核励起エネルギーのみで、その差δEはΔE >> δEをみたすとする。加えて、δEは核励起のエネルギー幅Γ₀に対し十分大きい（すなわちδE >> Γ₀）とする。このとき、各放射体から放射されるガンマ線のエネルギースペクトルはシングルラインとなるので、シングルラインの時間領域干渉計と呼ぶ。
　図1に示すように、ガンマ線が試料により散乱される際に検出器を配置した散乱角とガンマ線のエネルギーからBraggの式より決まる運動量qが移行する。図2(c)右図はあるqにおいて静的構造因子S(q)として表される空間的な相関が時間とともに緩和する様子を模式的に示しており、中間散乱関数S(q,t)と呼ばれる^[12][12] P. M. Chaikin, T. C. Lubensky: 現代の凝縮系物理学（吉岡書店、2000).。このエネルギー領域における表現（図2(c)左図）は動的構造因子と呼ばれる。
　図3に時間領域干渉計セットアップにおける、入射放射光パルスとガンマ線の時空ダイヤグラム上での経路を示す^[13,14][13] R. Röhlsberger: Nuclear Condensed Matter Physics with Synchrotron Radiation (Springer, 2005).
[14] M. Saito, R. Masuda, Y. Yoda, M. Seto: Sci. Rep. 7 (2017) 12558.。横軸としては、試料からある散乱角に散乱されるビームパス方向に沿った空間を考える。●は放射光による原子核の励起イベント、○は原子核の脱励起にともなうMössbauerガンマ線の前方方向への放射イベント、★は試料におけるRayleigh散乱イベントをそれぞれ表す。大部分の入射放射光は原子核を励起せず、試料により散乱され検出器で検出される。時空ダイヤグラム上での経路の傾きは光速を表す。この大部分の放射光パルスより、原子核の寿命τ₀～140 nsと同程度の時間スケールtだけ遅れて検出器で検出される光子（ガンマ線）が時空ダイヤグラム上でどのような経路を取りうるか考える。図1に示すように、ガンマ線放射体1中で核励起イベントを起こし、時間tだけ後にガンマ線“1”を放射し、試料によりRayleigh散乱され、ガンマ線放射体2中で核励起イベントを起こさずに検出器で検出される経路Iが考えられる。また、ガンマ線放射体1中で核励起イベントを起こさずに、試料によりRayleigh散乱され、ガンマ線放射体2中で核励起イベントを起こし、時間tだけ後にガンマ線“2”を放射し検出器で検出される経路IIが考えられる。検出器の時間分解能がh/δEよりも十分小さい場合、時間tにおいて観測された光子が経路I、経路IIのどちらを通ってきたかガンマ線のエネルギー差の観点からは不確定性原理により知ることができない。

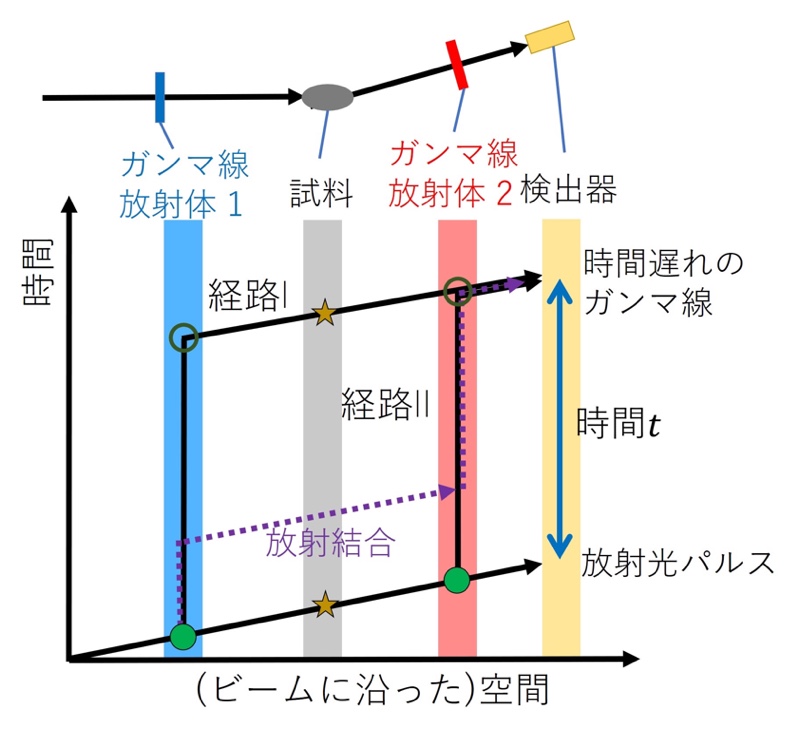
図3　時間領域干渉計におけるガンマ線・入射放射光の時間・空間経路

　ここで、δE >> Γの場合、図1中の放射結合と表記された点線の経路のように、ガンマ線放射体1、2の両方で核励起イベントを起こす経路をガンマ線が通る可能性は無視できる。
　通常、干渉計は空間で光を2手方向に分けることにより構築される。しかし本測定系は、比較的長いコヒーレンス時間を有するガンマ線を時空ダイヤグラム上で分けて干渉計を構築する大変ユニークなものである。これが時間領域干渉計という手法の名称の由来である。
　試料中での運動が無視できる場合、得られる時間スペクトルは図4(a)のように互いにわずかにエネルギーの異なるガンマ線1、2の干渉から“うなり”が生じる。時空ダイヤグラム上では、経路Iを通るガンマ線は、経路IIを通るガンマ線に対し時間tだけ遅れて試料によりRayleigh散乱される。ここで、ガンマ線の試料への運動量移行qに対応する、2π/qスケールの電子密度の空間的な相関が緩和する時間τがガンマ線の観測時間窓に入る場合を考える。このとき、経路I、IIを通ったガンマ線の位相の相関はτの時間スケールで消失する。その結果、図4(b)のように両経路のガンマ線の干渉パターン（うなり）がτの時間スケールで消え、干渉がない場合の時間スペクトルに移り変わる。これが“うなり”の緩和の時間領域上での解釈である。

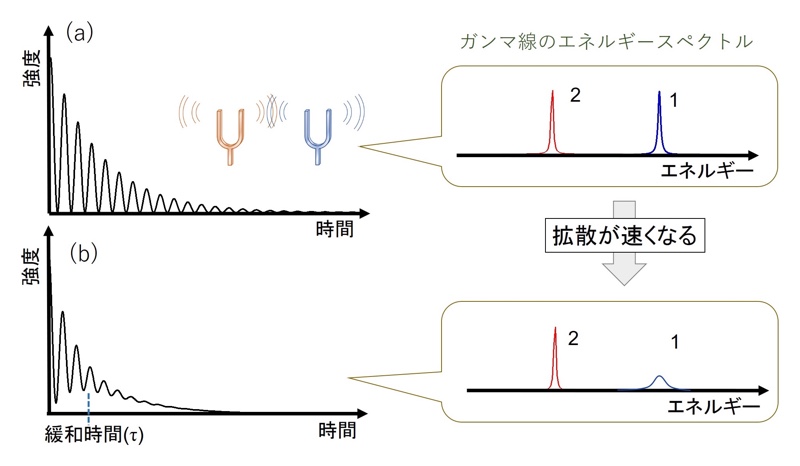
図4　シングルライン時間領域干渉計の時間スペクトルと対応するエネルギースペクトルの概念図　(a) 拡散がない場合、(b) 拡散が存在し、その緩和時間が観測時間窓に入る場合

3. マルチライン時間領域干渉計の時空ダイヤグラム描像
　ガンマ線放射体1、2として、それぞれで複数の異なるエネルギーで核励起を起こすような、マルチラインの時間領域干渉計を構築した場合に得られる時間スペクトルに関しても、基本的には同様の描像が成り立つ^[14][14] M. Saito, R. Masuda, Y. Yoda, M. Seto: Sci. Rep. 7 (2017) 12558.。すなわち、ガンマ線の時間スペクトルは、試料中のミクロな空間的な相関の緩和に伴い、経路I、IIを通ったガンマ線同士の干渉の現れである“うなり”の振幅が減少する（図5）。ガンマ線放射体1、2として様々な核励起エネルギーを有する放射体の選択が可能であるが、ガンマ線1、2間の干渉パターンがより劇的に干渉がない場合の時間スペクトルを変化させるような組み合わせを選択することで、試料の緩和の情報をより効率よく取得することが可能となる。これまで模擬実験スペクトルを生成し効率を評価する手法を確立することで、単純性と高効率を両立する組み合わせを見出している。それにより、ガンマ線の干渉パターンに、より効率的に情報をのせることを可能としている。これが、シングルライン法にくらべてマルチライン法の測定効率が大変高い要因の一つである。

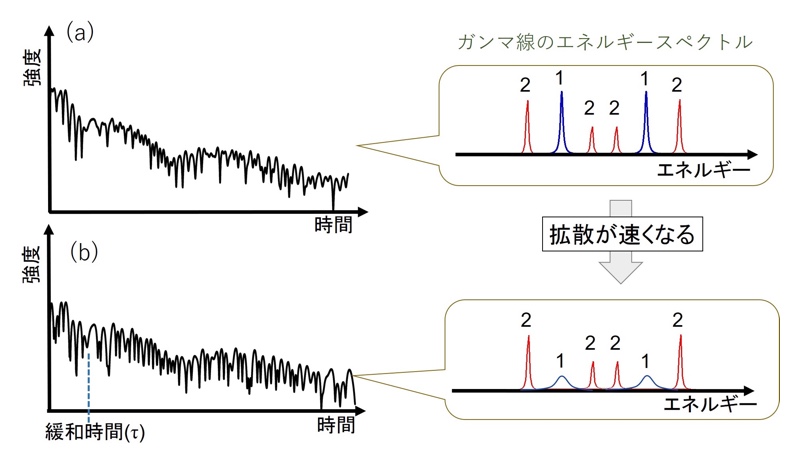
図5　マルチライン時間領域干渉計の時間スペクトルと対応するエネルギースペクトルの概念図　(a) 拡散がない場合、(b) 拡散が存在し、その緩和時間が観測時間窓に入る場合

4. 入射放射光のエネルギー幅の影響の時間領域描像―マルチライン法のもう一つの利点
　液体や固体中には格子振動や分子振動が存在し、その時間スケールは通常サブピコ秒程度である。この時間スケールは、meVに入射光を分光した場合の入射光のコヒーレンス時間と同程度のスケールとなる。我々は、入射放射光の時間コヒーレンスが試料との相互作用により低下しそれがガンマ線の時間スペクトルに影響すること、そしてマルチライン法を用いることで、このようなサブピコ秒スケールのダイナミクスの情報がナノ秒スケールの情報に加えて同時に得られることを示してきた^[14][14] M. Saito, R. Masuda, Y. Yoda, M. Seto: Sci. Rep. 7 (2017) 12558.。
　この理解のために、経路I、IIを図6(a)、(b)に個別に示しそれぞれ詳細に考察する。入射光のエネルギー幅がmeV程度であり、そのため入射光がΔT～サブピコ秒のコヒーレンス時間を有する場合を考える。2章と同様に、核励起を起こさない大部分のパルス放射光の強度ピークに対しt（>> ΔT）だけ遅れて検出されるガンマ線のとりうる経路を考える。このとき互いに干渉性を有するΔT程度の時間t’異なった時間成分の入射光の経路も考慮する必要がある。経路Iでは、検出器で大部分の散乱放射光から時間tだけ遅れて検出された光子は、入射時間に時間差t’があったとしても、試料において大部分の放射光が散乱される時間から常にtの時間後に散乱される。

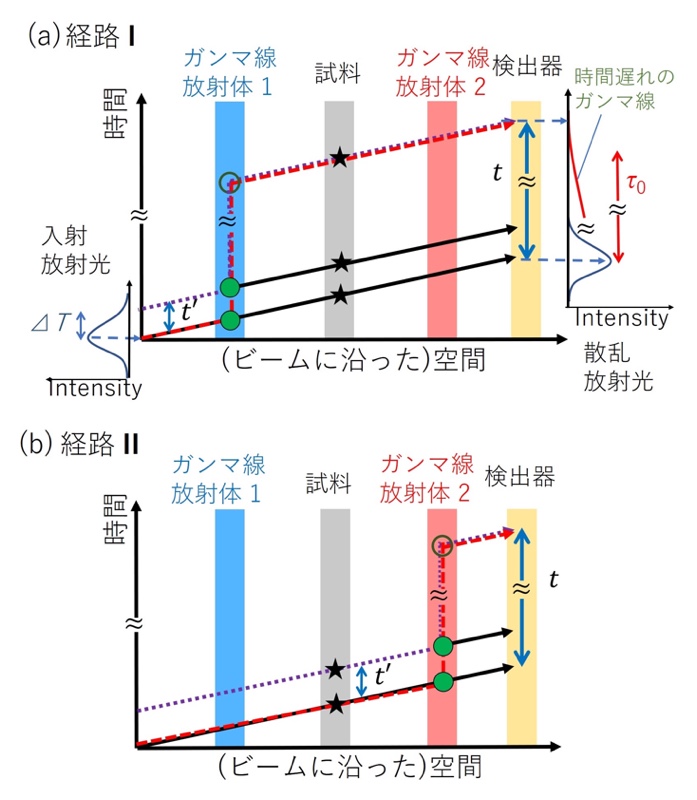
図6　入射放射光のエネルギー幅を考慮した時間領域干渉計におけるガンマ線・入射放射光の時間・空間経路　(a) 経路I、(b) 経路II

　一方経路IIでは、同様に核励起を起こさなかった散乱放射光の強度のピークから時間tだけ遅れて検出された光子は、入射時間に時間差t’分の差があった場合、試料においてもt’だけ異なった時間で散乱することになる。試料においてΔTの時間スケールにおいて運動がある場合、散乱電場の位相の相関は減少することになる。これは、位相が揃い前方方向に建設的に干渉する成分が減少することを意味するため、経路IIを通ったガンマ線2の散乱強度がガンマ線1に対して減少する効果として現れる。
　これまでガンマ線経路I、IIは同等であると考えられてきた^[8-10][8] A. Q. R. Baron et. al.: Phys. Rev. Lett. 79 (1997) 2823.
[9] G. V. Smirnov, V. G. Kohn, and W. Petry: Phys. Rev. B 63 (2001) 144303.
[10] G. V. Smirnov, et. al.: Phys. Rev. B 73 (2006) 184126.。しかし、ガンマ線放射過程が試料による散乱過程より後に起こると、散乱ガンマ線の強度が減少する場合があることが示された。シングルラインの時間領域干渉計を構築した場合、ガンマ線1、2の強度差があったとしても、ガンマ線1、2の干渉によるうなりが観測時間窓より速い時間スケールで緩和している効果と同じように見え、定量的にその寄与を決定できない。一方、ガンマ線1、2のエネルギースペクトルの形状が互いに異なる条件のマルチライン時間領域干渉計を構築することで、初めてガンマ線1、2の強度差を測定することが可能となり、サブピコ秒のダイナミクスの情報を引き出すことができる^[14][14] M. Saito, R. Masuda, Y. Yoda, M. Seto: Sci. Rep. 7 (2017) 12558.。これが、マルチライン時間領域干渉計の高速測定効率に加えたもう一つの利点である。
　図7にガンマ線時間スペクトルの干渉パターンを解析することで得られる時間0での値（すなわち静的構造因子S(q)）で規格化された中間散乱関数S(q,t)/S(q)を示す。結果はglycerolについて得られたものであり、観測時間窓内で十分緩和する255 Kにおけるq = 31 nm⁻¹で得られたS(q,t)/S(q)と、緩和が十分でない237.5 Kにおけるq = 14 nm⁻¹で得られたS(q,t)/S(q)を示す^[14][14] M. Saito, R. Masuda, Y. Yoda, M. Seto: Sci. Rep. 7 (2017) 12558.。現在ガンマ線の時間スペクトルを観測可能な時間窓（数ナノ秒～サブマイクロ秒）での観測結果に対し、そのフィット曲線を実線で示している。一方、ΔTに対応するサブピコ秒の時間スケールにおいても、典型的なS(q,t)/S(q)の値をプロットすることができる。この点がナノ秒領域のフィット曲線から外れているのはサブピコ秒の時間スケールで分子振動やボゾンピークにより中間散乱関数が緩和していることを表している^[15][15] F. Bencivenga, et. al.: Nature 520 (2005) 205.。このように、時間領域干渉計は2つのエネルギー分解能関数を有するユニークな測定系で、対応する異なる時間スケールのダイナミクスの情報を、マルチライン化することで同時に得ることができる。なお、この節において時間領域上で解説した描像は、エネルギー領域上のスペクトル形状の議論からも示すことができるが、紙面の都合上割愛する。

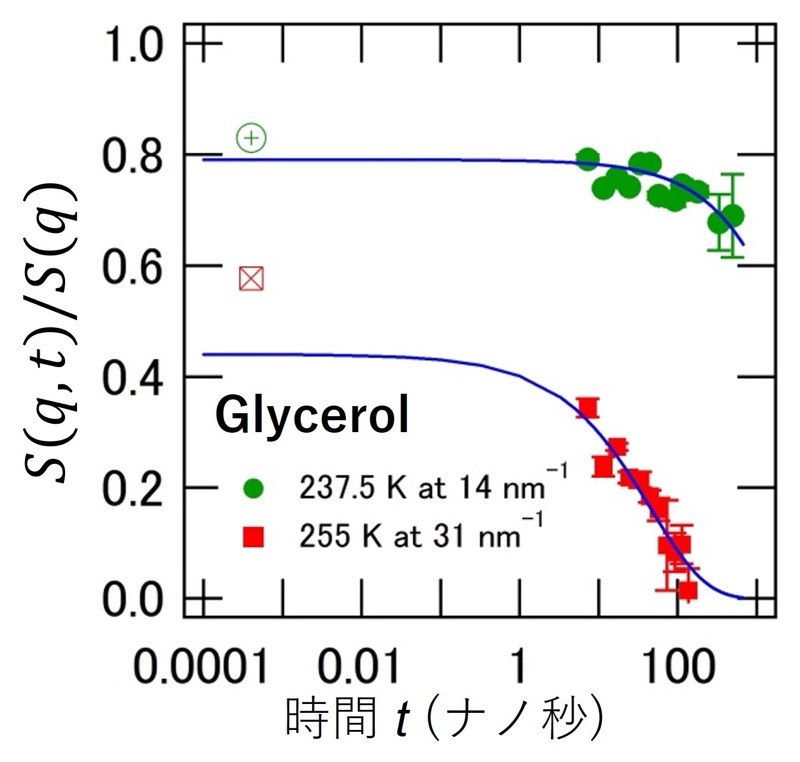
図7　Glycerolに対して得られた規格化された中間散乱関数S(q,t)/S(q)の例

5. まとめと展望
　本稿では、ガンマ線の長い時間コヒーレンスの観点から時間領域干渉計の原理の解説を試みた。今後SPring-8-IIの完成により入射放射光の空間コヒーレンスが向上することから、高い時間・空間コヒーレンス有するガンマ線を生成することが可能となると考えられる。このような高コヒーレントなガンマ線によりユニークな物性研究が加速すると考えられる。

参考文献
[1] 菊田惺志：X線散乱と放射光科学 基礎編（東京大学出版会、2011）
[2] G. V. Smirnov: Hyperfine Interactions 123/124 (1999) 31.
[3] M. Yabashi, K. Tamasaku, S. Kikuta, T. Ishikawa: Rev. Sci. Instrum. 72 (2001) 4080.
[4] 瀬戸誠：日本結晶学会誌 43 (2001) 405.
[5] 瀬戸誠：固体物理 44 (2009) 27.
[6] 齋藤真器名：SPring-8/SACLA利用者情報 22 (2017) 91.
[7] 齋藤真器名：固体物理 47 (2012) 11.
[8] A. Q. R. Baron et. al.: Phys. Rev. Lett. 79 (1997) 2823.
[9] G. V. Smirnov, V. G. Kohn, and W. Petry: Phys. Rev. B 63 (2001) 144303.
[10] G. V. Smirnov, et. al.: Phys. Rev. B 73 (2006) 184126.
[11] T. Ishikawa, Y. Yoda, K. Izumi, C. K. Suzuki, X. W. Zhang, M. Ando, and S. Kikuta: Rev. Sci. Instrum. 63 (1992) 1015.
[12] P. M. Chaikin, T. C. Lubensky: 現代の凝縮系物理学（吉岡書店、2000).
[13] R. Röhlsberger: Nuclear Condensed Matter Physics with Synchrotron Radiation (Springer, 2005).
[14] M. Saito, R. Masuda, Y. Yoda, M. Seto: Sci. Rep. 7 (2017) 12558.
[15] F. Bencivenga, et. al.: Nature 520 (2005) 205.

齋藤　真器名　SAITO Makina
京都大学　複合原子力科学研究所
〒590-0494　大阪府泉南郡熊取町朝代西2丁目
TEL : 072-451-2680
e-mail : msaito@rri.kyoto-u.ac.jp