Volume 23, No.4 Pages 310 - 315

1. はじめに
　X線トポグラフィは単結晶の欠陥や析出物^[1-4][1] D. K. Bowen and B. K. Tanner: High Resolution X-Ray Diffraction and Topography (Taylor & Francis, London, 1998).
[2] J. Appl. Phys. 28, No.4A, A17-A91 (1995), Special Issue: X-ray topography and high resolution diffraction.
[3] J. M. Yi, J. H. Je, Y. S. Chu, Y. Zhong, Y. Hwu and G. Margaritondo: Appl. Phys. Lett. 89 (2006) 074103.
[4] J. Japanese Association for Crystal Growth 54, No.1 (2012), Special Issue: Recent Advances in X-ray Topography [in Japanese].などの転位やその他の欠陥を調べるために広く使用されており、特に転位のバーガースベクトルの決定に有用である。通常トポグラフでは、結晶内の個々の転位を視覚化するために、X線フィルムや原子核乾板を使用して記録する。各転位のバーガースベクトルは、異なる回折ビームを使用するいくつかの画像からコントラストの消失によって決定されるが、これらの画像は、回折の光学配置に依存して結晶の元の形状から変形する。元の形状を回復するために、トポグラフ上で1つまたは2つの方向に画像解析ソフトなどを用いて電子的に縮小拡大されるが、この操作は空間分解能を低下させる。2波近似のX線回折の動力学理論^[5][5] For example, A. Authier: Dynamical Theory of X-Ray Diffraction (Oxford University Press, Oxford, 2001).によると、回折されたビームと前方透過されたビームによって得られる転位像は、結晶の吸収率が小さい場合（µt < 1、ここでµは線吸収係数、tは試料中のX線ビームの侵入深さである）、コントラストが反転する。以下、前者のビームを用いたトポグラフを暗視野トポグラフ、後者のそれを明視野トポグラフと呼ぶ。したがって、暗視野または明視野トポグラフィのいずれかを使用して、転位のバーガースベクトルを決定することができる。Yiらは、明視野透過型電子顕微鏡法（TEM）と同様に、4H-SiC結晶の格子歪みを調べるために、明視野X線ビームトポグラフィを利用している^[3][3] J. M. Yi, J. H. Je, Y. S. Chu, Y. Zhong, Y. Hwu and G. Margaritondo: Appl. Phys. Lett. 89 (2006) 074103.。
　本研究では、複数の回折が同時に生じる多波近似条件近傍で、明視野トポグラフを撮像する。このため、トポグラフ像に形状変形が生じない。コヒーレントなX線ビームを用いて多波回折を生じさせたときのビームの干渉パターンは、沖津らによる報告があるが^[6,7][6] K. Okitsu: Acta Crystallogr., Sect. A 59 (2003) 235-244.
[7] K. Okitsu, Y. Imai, Y. Ueji and Y. Yoda: Acta Crystallogr., Sect. A 59 (2003) 311-316.、本研究で用いたビームはインコヒーレントであるため、トポグラフ像にこれらの干渉パターンが際立つことはない。

2. 多波近似条件
　完全性が高い結晶にX線が入射する場合、結晶中には入射方向の波（O波）と回折方向の波（G波）が生じる。通常の実験条件では結晶中にはG波は1つだけであり（その他の波はとても小さい）、O波と合わせて2波近似と呼ばれる。それに対して、特定の指数の回折を考える場合、結晶と入射ビームのアラインメントを精密に調整すると、複数のG波を励起することができる。この条件が満たされる場合を多波近似条件と呼ぶ。
　本実験で用いたサファイア結晶は六方晶であり、例えば、4220、3300、3030、1210、1120の5つの回折波を同時に励起することができる。この場合、O波と合わせて結晶中に6つの波が生じるため6波近似と言う。同時に回折が生じる場合を実空間で説明すると以下の通りである。図1(a)のように六方晶のa1、a2、a3、c軸をとる。また、図1(b)に示すように、(4220)、(3300)、(3030)、(1210)、(1120)面に平行な面をとる。図1(c)のようにxyz座標をとると、図1(b)の矢印で示した5つの面の法線ベクトルは、(4220)面から順に、(0, 1, 0)、(0, cos30°, sin30°)、(0, cos30°, -sin30°)、(0, cos60°, -sin60°)、(0, cos60°, sin60°)で表される。以下同時に生じる回折に関して、4220回折と3300回折のみについて述べる。4220回折のブラッグ角をθ_{4-2-2 0}とし、結晶を図1(b)の状態からz軸まわりにθ_{4-2-2 0}だけまわすと、(4220)、(3300)面の法線ベクトルはそれぞれ、(-sinθ_{4-2-2 0}, cosθ_{4-2-2 0}, 0)、(-sinθ_{4-2-2 0}・cos30°, cosθ_{4-2-2 0}・cos30°, sin30°)となる（図1(d)参照）。X線と回折面のなす角は、X線の方向ベクトルと回折面の法線ベクトルの内積を使って求めることができる。図1(e)のように、X線の方向ベクトルと回折面の法線ベクトルのなす角をθ、X線の方向ベクトルと回折面のなす角をαとする。方向ベクトル、法線ベクトル共に大きさは1だから、その内積は、

cosθ = cos(90° + α) = -sinα

である。これを先程のθ_{4-2-2 0}だけ回転した(4220)面の法線ベクトルn₁(-sinθ_{4-2-2 0}, cosθ_{4-2-2 0}, 0)とX線の方向ベクトルl(1, 0, 0)に適用すると、

n₁・l = -sinθ_{4-2-2 0}

これが、-sinαに等しいので、θ_{4-2-2 0} = αと当然の結果が得られる。

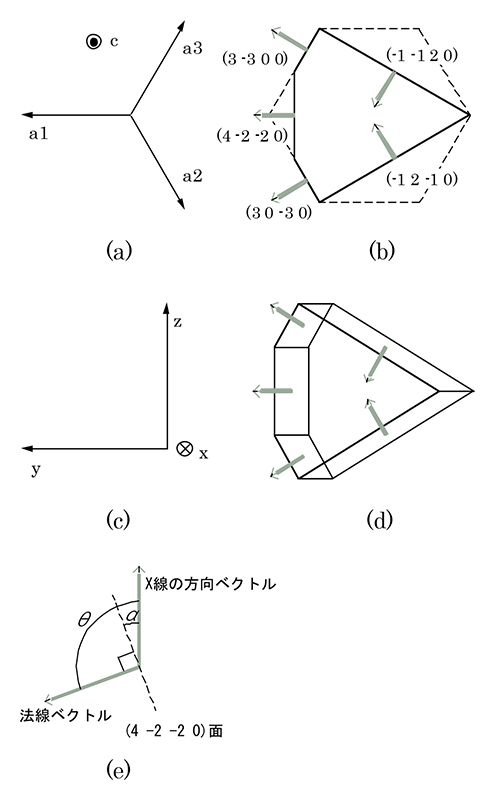
図1　(a) 六方晶の基本ベクトル、(b) (4220)、(3300)、(3030)、(1210)、(1120)面、(c) 座標軸、(d) (b)の状態からz軸周りにθ_{4-2-2 0}だけ回転したときの模式図、(e) 法線ベクトルと方向ベクトルの関係。

　同様にθ_{4-2-2 0}だけ回転した(3-3 0 0)面の法線ベクトルn₂(-sinθ_{4-2-2 0}・cos30°, cosθ_{4-2-2 0}・cos30°, sin30°)とX線の方向ベクトルl(1, 0, 0)、X線と回折面のなす角α₁に適用すると、

n₂・l = -sinθ_{4-2-2 0}・cos30°

= -sinθ_{4-2-2 0} = -sinα₁

である。ブラッグの法則から、sinθ_{4-2-2 0} = λ/2d_{4-2-2 0}だから、これを上式に代入して、

λ = d_{4-4-2 0} sinα₁

を得る。六方晶では、d_{3-3 0 0} = d_{4-2-2 0}なので、上式は、

λ = 2d_{3-3 0 0}・sinα₁

となり、3300回折も同時に回折条件を満たすことがわかる。

3. 実験
　実験はSPring-8 BL24XU（兵庫県ID）で行った。二結晶分光器で15 keVのX線を選択し、4象限スリットで1 × 1 mm²にビームを整形した。このときの波長幅（Δλ/λ）は3 × 10⁻⁴である。試料は、鏡面研磨したサファイア単結晶で表面は(0001)面である。撮像は可視変換型のCMOSカメラ（Hamamatsu, C11440-22CU）で、蛍光体にはGAGG（Gd₃Al₂Ga₃O₁₂）シンチレータを用いた。この組み合わせで、1 µmのラインアンドスペースの分離が可能である。その光学配置を図2に示す。

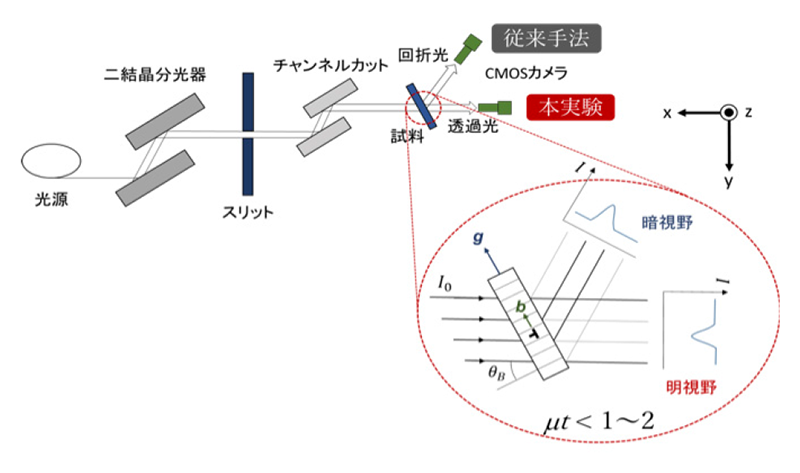
図2　本実験での実験配置。

　図3(a)は6波を励起したときの蛍光板像である。Oで示したスポットは、サファイア結晶上の点Pを透過した透過ビームであり、A−Eのそれは、それぞれ4220、3300、3030、1210、1120の5つの回折ビームである。図3(a)の状態からOBを結ぶ直線を回転軸に結晶をわずか0.1°程度回転すると図3(b)の蛍光板像が得られる。このとき結晶内には入射方向の波と3300回折の方向の波の2波近似が成り立つ。その他の回折もOとその回折スポットを結ぶ直線の周りのわずかな回転で2波近似が成立する。このため、回折ベクトルを変更しても入射方向からみた結晶の外形はほとんど変化がなく、また透過ビームを撮像するためトポグラフ像に現れる転位線の位置や形状も変化しない。

図3　(a) 6波近似時の蛍光板像、(b) 2波近似時の蛍光板像。

4. 結果と考察
　図4(a)、(b)はそれぞれ図3(a)、(b)の6波近似状態と2波近似状態でのトポグラフ像で、水平方向6ショット、鉛直方向5ショットをつなぎ合わせている。これらのトポグラフ像では、転位線の位置や形状に変化がないことがわかる。これは、明視野かつ多波近似近傍でのトポグラフ撮像のためである。

図4　(a) 明視野6波近似条件でのトポグラフ像。CMOSカメラで撮像。図3(a)の6波を励起した状態で撮像。(b) 明視野2波近似条件でのトポグラフ像。CMOSカメラで撮像。図3(b)の2波を励起した状態で撮像。(c) 暗視野トポグラフ像。CMOSカメラで撮像。図3(a)のスポットAを励起した状態で撮像。(d) 実験室光源でのトポグラフ像。X線フィルムで撮像。(a)～(c)は水平方向6ショット、鉛直方向5ショットをつなぎ合わせたもの。(a)と(b)の比較からBで示す転位線のバーガースベクトルがOB方向に直交し、またこの転位の伸びている方向がOB方向と平行であるため、刃状転位であることがわかる。(c)の黄色丸で示した領域の転位線の間隔が、(a)の像と比べて広がっていることが確認できる。これは回折像を撮影したため、像の変形が起こっていることを示す。(a)～(c)の画像の分解能は、(d)の画像の分解能より格段に向上していることが確認できる。

　図4(a)で、Aで示された転位線は図4(b)でも現れているのに対し、Bで示された転位線は、図4(b)ではコントラストが消失していることがわかる。一般に回折ベクトルgと転位まわりの歪みを表すバーガースベクトルbが直交するとき、そのコントラストは消失または弱くなる。このことから、Bで示した転位線のバーガースベクトルはOB方向に直交でまた、転位線の伸びている方向がOB方向であるため、この転位は刃状転位であることがわかる。これは、明視野トポグラフィであっても、通常のLang法で用いられる転位のバーガースベクトルの決定が可能であることを示している。
　図4(c)は、4220回折のみを励起したときの暗視野トポグラフ像（回折像）で、図4(a)と同じ領域を撮像している。このトポグラフ像は、おおむね図4(a)のコントラストの反転であるが、一方、黄色丸で囲った領域の転位線の間隔が広がっていることが確認できる。これは、暗視野トポグラフィでの転位線の形状の変形である。
　図4(d)は実験室光源でX線フィルムを用いて取得した同じ領域のトポグラフ像である。SPring-8でCMOSカメラを用いた撮像の空間分解能が高いことがわかる。
　図5(a)、(b)は、図4(a)、(b)と同じ条件で比較的転位密度の高い領域を撮像したトポグラフ像の拡大図である。下側の比較的転位密度の高い領域でも個々の転位線が細い線として分離されている。この領域の転位密度は3 × 10⁴ /cm²程度であり、これまでX線トポグラフィでは分離が難しいとされていた10⁴ /cm²でも撮像可能であることを示している。この要因としては、検出器の空間分解能や検出感度の高い線形性によるところだけでなく、SPring-8の輝度が高いためでもある。CMOSカメラでの1ショットの露光は、数10 msecで十分S/N比の高い画像がリアルタイムで得られる。このためロッキングカーブのピークまたはテールでの撮像も迅速で、転位線を細く撮像できる条件調整が容易であるためである。

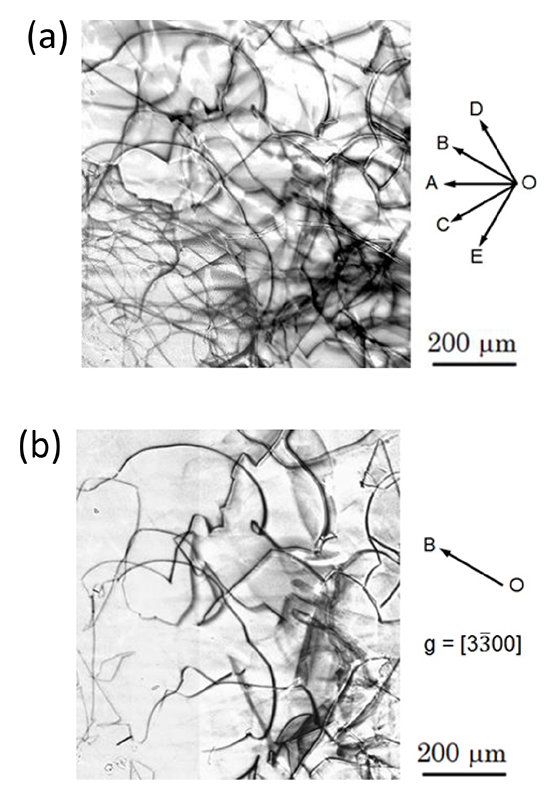
図5　高転位密度領域のトポグラフ像。(a) 6波近似条件でのトポグラフ像。(b) 2波近似条件でのトポグラフ像。下側の領域での転位密度は3 × 10⁴ /cm²程度である。

　放射光を用いたトポグラフィでは、Be窓や分光器が原因の入射ビームの強度ムラがしばしば問題になるが、明視野トポグラフィではその問題も解決可能である。図6(a)はある領域で撮像したオリジナルのトポグラフ像、図6(b)はロッキングカーブのピークから結晶をわずかに回転し、回折条件を満たさない状態で得られたビームの透過像である。図6(a)の強度分布を図6(b)の強度分布で除して得られた像が図6(c)である。図6(a)と比べて、バックグラウンドの強度ムラが解消されている。

図6　(a) オリジナルのトポグラフ像、(b) ロッキングカーブのピークから結晶をわずかに回転し、回折条件を満たさない状態で得られたビームの透過像。(a)の強度分布を(b)の強度分布で除して得られた像が(c)である。

5. まとめ
　本研究では、多波近似条件近傍での明視野トポグラフィをサファイア結晶に適用し、転位線の観察を行った。高輝度なX線光源を利用し、画像検出器にCMOSカメラを用いることで、以下に述べるメリットがあることを示した。

1. 高輝度放射光を利用し、検出器に高空間分解能・検出感度の高線形性を持つCMOSカメラを用いることで、高分解能のトポグラフ像が得られる。
これまで10⁴ /cm²以上の転位密度を持つ試料の観察が困難と考えられていたX線トポグラフが10⁵ /cm²程度のそれの観察まで可能性があることを示す。一方で、電子顕微鏡では10⁶ /cm²以下の転位密度の試料の観察は困難とされており、観察の難しい領域を簡便な方法で埋める可能性を示した。

2. 回折ベクトルを変更しても転位線の位置や形状が変形することはない。これは、コントラストの消失から判断する転位のバーガースベクトルの決定に大変有用である。

3. 回折ベクトルの変更が容易で、また検出器の移動がないため、異なる回折ベクトル撮像が迅速である。

4. リアルタイム観察が可能であるため、良好なコントラストを得ることができる撮像条件の調整が迅速である。

参考文献
[1] D. K. Bowen and B. K. Tanner: High Resolution X-Ray Diffraction and Topography (Taylor & Francis, London, 1998).
[2] J. Appl. Phys. 28, No.4A, A17-A91 (1995), Special Issue: X-ray topography and high resolution diffraction.
[3] J. M. Yi, J. H. Je, Y. S. Chu, Y. Zhong, Y. Hwu and G. Margaritondo: Appl. Phys. Lett. 89 (2006) 074103.
[4] J. Japanese Association for Crystal Growth 54, No.1 (2012), Special Issue: Recent Advances in X-ray Topography [in Japanese].
[5] For example, A. Authier: Dynamical Theory of X-Ray Diffraction (Oxford University Press, Oxford, 2001).
[6] K. Okitsu: Acta Crystallogr., Sect. A 59 (2003) 235-244.
[7] K. Okitsu, Y. Imai, Y. Ueji and Y. Yoda: Acta Crystallogr., Sect. A 59 (2003) 311-316.

津坂　佳幸　TSUSAKA Yoshiyuki
兵庫県立大学　大学院物質理学研究科
〒679-1297　兵庫県赤穂郡上郡町光都3-2-1
TEL : 0791-58-0231
e-mail : tsusaka@sci.u-hyogo.ac.jp

鶴丸　哲也　TSURUMARU Tetsuya
兵庫県立大学　大学院物質理学研究科
〒679-1297　兵庫県赤穂郡上郡町光都3-2-1
TEL : 0791-58-0229
e-mail : ri16q025@stkt.u-hyogo.ac.jp

水落　博之　MIZUOCHI Hiroyuki
兵庫県立大学　大学院物質理学研究科
〒679-1297　兵庫県赤穂郡上郡町光都3-2-1
TEL : 0791-58-0229
e-mail : ri17x025@stkt.u-hyogo.ac.jp

鎌本　春花　KAMAMOTO Haruka
兵庫県立大学　大学院物質理学研究科
〒679-1297　兵庫県赤穂郡上郡町光都3-2-1
TEL : 0791-58-0229
e-mail : ri17b007@stkt.u-hyogo.ac.jp

藤田　優　FUJITA Yu
兵庫県立大学　大学院物質理学研究科
〒679-1297　兵庫県赤穂郡上郡町光都3-2-1
TEL : 0791-58-0229
e-mail : ri18x026@stkt.u-hyogo.ac.jp

松井　純爾　MATSUI Junji
兵庫県立大学　放射光ナノテクセンター
〒679-5165　兵庫県たつの市新宮町光都1-49-2
TEL : 0791-58-1415
e-mail : matsui@hyogo-bl.jp

産業利用の課題を随時受け付けております。
詳細につきましては下記ウェブサイトまたは連絡先までお問合せください。
http://www.hyogo-bl.jp/
兵庫県ビームライン事務局
TEL : 0791-58-1961
e-mail : nanochan@hyogo-bl.jp