Volume 23, No.3 Pages 219 - 222

1. Introduction
　Magnetic Compton scattering is an established experimental technique, used extensively on beamline BL08W at SPring-8. The objective of this long term project was to perform experiments using our "Spectromag" cryomagnet sample environment, which is capable of applying magnetic fields up to 9 T, and temperatures down to 1.5 K. Previously, we had commissioned this cryomagnet for use on BL08W via long term project 2012B0045.
　The magnetic Compton scattering experimental technique enables the study of the spin resolved electron momentum density of a magnetic material via measurements of the inelastic scattering of high energy circularly polarised X-rays. The interpretation of the results typically requires electronic structure calculations, and hence, the technique provides insight into the underlying electronic structure of the material studied. The method is suitable for materials with a net magnetic moment: ferromagnets and ferrimagnets, and also other systems where the applied magnetic field induces a moment.
　The experiments utilise non-resonant inelastic, or "Compton", scattering of monochromatic high energy (typically 175 keV) photons from the sample. Figure 1 depicts the experimental geometry. The high scattering angle, of 175° is used to optimise the magnetic signal and the experimental resolution. When the X-rays are inelastically scattered by the electrons in the sample, the photon energy distribution measured at a set scattering angle is Doppler broadened because of the electrons' momentum distribution. A measurement of the photon energy spectrum can be directly related to a 1-dimensional projection of the electron momentum distribution of the sample. In order to make the spin-resolved measurements, circularly polarised photons are required, and a reversible magnetic field is applied to the sample. This permits a spin-dependent term in the scattering cross-section to be exploited. A measurement involves reversing the applied field and taking the difference between the two spectra collected. The charge scattering cancels out, leaving the spin contribution. Hence the resultant measurement, or magnetic Compton profile (MCP), represents the electron momentum density of only those electrons that contribute to the spin magnetic moment of the sample.

Figure 1  A schematic representation of the geometry adopted for magnetic Compton scattering experiments.

2. Interpretation and Application of magnetic Compton scattering
　Because only those electrons that contribute to the spin moment of the sample contribute to the MCP, the sample's spin magnetic moment can be determined. Such measurements can provide valuable information in systems where the spin and orbital moments contributions to a known bulk magnetic moment are unknown or not fully understood. For example, in many 5d and 5f compounds the crystalline electric field and spin-orbit coupling contributions to the ground state are finely balanced, leading to complex electronic structures and competing magnetic states. One consequence of this delicate balance is a high sensitivity of the values of the spin and orbital moments to the details of the electronic structure. Magnetic Compton scattering has an important role to play here as it permits the determination of the ground state spin and orbital magnetic moments (when combined with bulk magnetisation measurements); for example see^[1][1] M. W. Butchers et al.: Phys. Rev. B 92 (2015) 121107(R).. In this report we demonstrate this for the 5d system Nd₂Ir₂O₇.
　In order to interpret measured MCPs, electronic structure calculations are often used. A number of theoretical approaches are possible typically using density function theory (DFT) in the local spin density or generalised gradient approximations. The effects of the Fermi surface are often observed in metallic materials, and such calculations can help give an understanding of the underlying electronic properties. The electronic structure calculations can be used as the basis for fitting to the data to reveal the physics, rather than relying on a purely ab initio approach. For example, see our previous work based on measurements on BL08W, where the method reveals ferrimagnetism rather than ferromagnetism in the Fe-rich NbFe₂^[2][2] T. D. Haynes et al.: Phys. Rev. B 85 (2012) 115137.. In this article we will give a progress report on our work on the itinerant metamagnet Sr₃Ru₂O₇, where we used the "Elk" electronic structure code^[3][3] D. Ernsting et al.: J. Phys. Condens. Matter 26 (2014) 495501..

3. Experimental Details
3.1 The experimental set up
　Monochromatic circularly polarised X-rays of energy 182 keV were used for these experiments, which are available on beamline BL08W. The beamline's helical wiggler was used to obtain the required circular polarisation. The scattering geometry adopted is the standard approach, and is based on that depicted in figure 1. The scattering angle is approximately 172 degrees, and the experiments use the beamline's own 10-element solid state Ge detector to measure the energy spectrum of the scattered X-rays. The known scattering cross-section is then used to obtain the electron momentum density as resolved along the X-ray scattering vector. Because of the high energy photons, and the requirements for being able to gain sufficient statistical accuracy, typical sample sizes are around 8 mm³, although smaller samples are feasible.

3.2 Experimental Procedure
　As discussed above, obtaining an MCP requires a difference measurement to be made. To do this, the magnetic field is reversed and data collected for fields parallel and anti-parallel to the X-ray scattering vector. The magnetic signal is often less than 0.5% of the charge scattering, and hence very good normalisation is crucial. The procedure adopted is the "ABBA" method, where A and B represent the two magnetic field directions. The counting times between field reversals are set according to the field required, and can be as long as 30 minutes. In our previous long term project, we were able to show that very good normalisation is feasible even for such long counting times. Our further refinements during this project have shown us that this is actually limited by the magnitude of the signal. For systems with very small signals, which are defined in terms of ratio of the spin moment to the number of electrons per formula unit, we found that the normalisation became unachievable because of some (very small) instabilities in the counting chain over long times.

4. Results and Discussion
　During the course of the long term project a number of materials have been studied. In this article, we discuss two of our investigations, in order to illustrate how magnetic Compton scattering can be utilised to contribute to our understanding of magnetic materials.

4.1 The itinerant metamagnet Sr₃Ru₂O₇
　Sr₃Ru₂O₇ is considered to be a system that exhibits quantum criticality (for example, see^[4][4] Y. Tokiwa et al.: Phys. Rev. Lett 116 (2016) 226402. and references therein). It has a low temperature metamagnetic transition which may be related to a change in the topology of the Fermi surface. The recent observation of spin-density wave (SDW) order^[5][5] C. Lester et al.: Nature Materials 14 (2015) 373-378. appears to support earlier ideas connecting the shape of the Fermi surface with the electronic instability^[6,7][6] L. Capogna et al.: Phys. Rev. B 67 (2003) 012504.
[7] S. Ramos et al.: Physica B 403 (2008) 1270-1272.. It is proposed that, as the magnetisation changes through the metamagnetic transition, the underlying Fermi surface itself changes, going through an "electronic topological transition". The objective of our experiment was to use the sensitivity of magnetic Compton scattering to the electronic structure and Fermi surface effects as a tool to determine the correct theoretical description of the metamagnetic state.
　For our study, we have combined experimental measurements along three high-symmetry crystallographic directions with electronic structure calculations. The experimental data for one crystallographic direction shown in figure 2, together with the results of one of our calculations. The experimental value of the spin moment determined from our measurement at temperature T = 1.5 K and in an applied magnetic field of B = 6 T is small (0.71 ± 0.02 μ_B). Since Sr₃Ru₂O₇ is metamagnetic it is non-magnetic in zero applied field: consistently with this, ab initio calculations do not predict exchange splitting of the electronic bands and hence predict there to be no magnetic moment. For our calculation shown in figure 2, we fixed the spin moment to agree with the experimental value in order to simulate the metamagnetic phase. It is clear that the predicted profile does follow the overall shape of the experimental data, but there are important differences, especially between 0.5 - 1.5 a.u. (atomic units). As will be discussed elsewhere, we have performed several calculations where the spin moment (and hence the spin splitting of the electron bands) is fixed at different values higher than the experimental moment: whilst such calculations by definition give the wrong signal size, they show a much improved shape. We intend to make field-dependent Fermi surface measurements on this system, if we are successful in obtaining the UK funding for our new research project: for example our current measurements are in the metamagnetic phase, but we wish to study the transition itself to look for evidence of the proposed electronic topological transition.

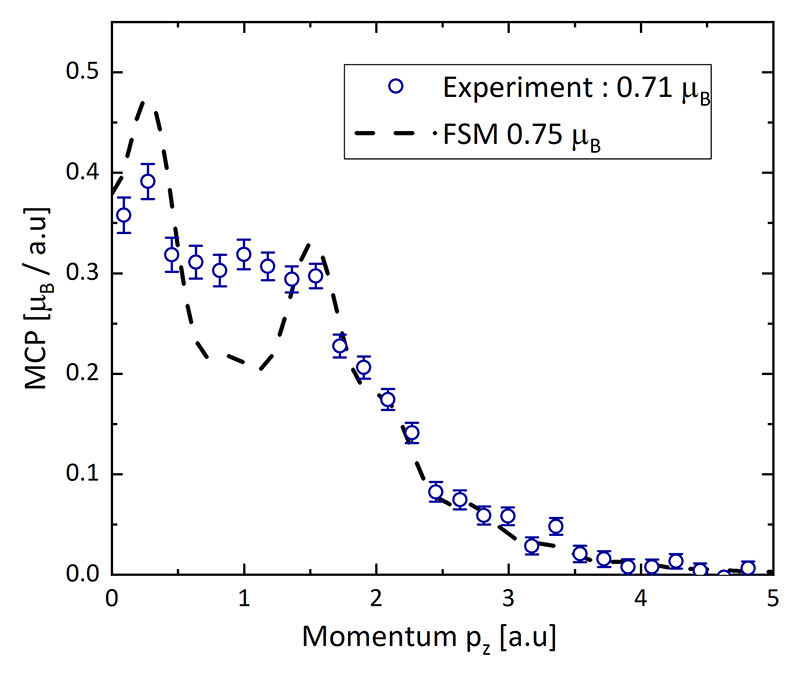
Figure 2  MCP for Sr₃Ru₂O₇ measured at 1.5 K in an applied field of 6 T, for the [100] crystallographic direction. "FSM" stands for the "fixed spin moment" values used in the calculation presented. Particular features can be observed at the origin and at p_z = 1 a.u., where there are clear discrepancies between the experiment and the calculation.

4.2 Spin and orbital moments in Nd₂Ir₂O₇
　The iridate compounds are particularly interesting because the crystalline electric field and spin-orbit coupling contributions to the ground state are finely balanced for the magnetically-active 5d electrons, leading to complex electronic structures and competing magnetic states. In the case of Nd₂Ir₂O₇, Muon spectroscopy papers from two groups suggest differing magnetic properties: in one case^[8,9][8] K. Matsuhira et al.: JPSJ 82 (2013) 023706.
[9] S. M. Disseler et al.: Phys. Rev. B 85 (2012) 174441., there is a low temperature Ir moment, but no ordered Nd moment; in the other^[10][10] S. M. Disseler et al.: Phys. Rev. B 87 (2013) 060403(R)., the Ir orders at T = 30 K and the Nd at T = 9 K. New theoretical^[11][11] H. Zhang et al.: Phys. Rev. Lett 118 (2017) 026404. and muon work^[12][12] R. Asih et al.: JPSJ 86 (2017) 024705., both concerning the magnetic moments, which we can address. Nd₂Ir₂O₇ is metallic above T ~33 K, at which temperature it undergoes a metal-insulator transition (MIT). A giant magnetoresistance (GMR) of up to 3000% has been found^[13][13] H. Guo et al.: Phys. Rev. B 88 (2013) 060411(R).. Such a high GMR only occurs for the Nd member of the series: a large anisotropic 4f moment appears crucial.
　We have used magnetic Compton scattering in conjunction with GAMESS molecular orbital calculations to study the origin of the magnetisation. GAMESS gives a guide to the Compton profile contributions of the Nd 4f and Ir 5d orbitals. We have studied the temperature dependence in detail, collecting data across the proposed electronic transitions.
　We have made measurements in a magnetic field of 5 T and at temperatures from 2.0 K up to 60 K. We have found that the Nd 4f moment persists at all temperatures. However, as shown in figure 3, the spin moment and the ratio of the spin to orbital moments appear to exhibit different temperature dependencies. It appears that the spin moment drops above 10 K, with no change in the spin/orbit ratio, probably dominated by the reduction of Nd 4f moment with increasing temperature. There is also a distinct change in the ratio at around 30~40 K, together with a possible small increase in the spin moment, near the proposed MIT. We are now developing a model in order to analyse the Ir contribution, which we expect will complete our interpretation.

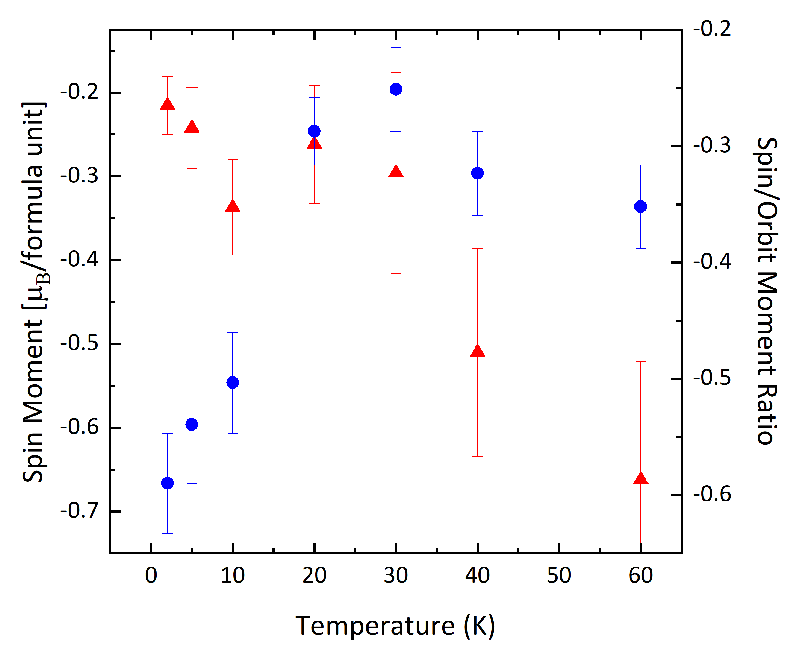
Figure 3  Temperature dependence of the spin moment (blue circles) and ratio of the spin to orbital moments (red triangles) in Nd₂Ir₂O₇. A large change appears in the spin moment at T = 10~20 K but in the ratio at T = 30~40 K.

5. Summary
　Magnetic Compton scattering experiments provide a considerable amount of information in magnetic materials. It is particularly useful to investigate the spin contribution in systems where both spin and orbital contributions may exist. Furthermore, its sensitivity to the underlying electronic structure can be invaluable when investigating the electronic properties of materials and how these lead to the materials' properties. Our cryomagnet sample environment is capable of providing magnetic fields up to 9 T and temperatures down to 1.5 K. Anyone who is interested in exploiting magnetic Compton scattering as part of their research is very welcome to use our magnet for their experiments at SPring-8.

Acknowledgments
　We gratefully acknowledge the provision of beam time at SPring-8 by JASRI (Proposal number 2016A0131). We would also like to thank N. Tsuji, M. Itou, Y. Sakurai and the staff for their support and assistance.

References
[1] M. W. Butchers et al.: Phys. Rev. B 92 (2015) 121107(R).
[2] T. D. Haynes et al.: Phys. Rev. B 85 (2012) 115137.
[3] D. Ernsting et al.: J. Phys. Condens. Matter 26 (2014) 495501.
[4] Y. Tokiwa et al.: Phys. Rev. Lett 116 (2016) 226402.
[5] C. Lester et al.: Nature Materials 14 (2015) 373-378.
[6] L. Capogna et al.: Phys. Rev. B 67 (2003) 012504.
[7] S. Ramos et al.: Physica B 403 (2008) 1270-1272.
[8] K. Matsuhira et al.: JPSJ 82 (2013) 023706.
[9] S. M. Disseler et al.: Phys. Rev. B 85 (2012) 174441.
[10] S. M. Disseler et al.: Phys. Rev. B 87 (2013) 060403(R).
[11] H. Zhang et al.: Phys. Rev. Lett 118 (2017) 026404.
[12] R. Asih et al.: JPSJ 86 (2017) 024705.
[13] H. Guo et al.: Phys. Rev. B 88 (2013) 060411(R).