Volume 23, No.1 Pages 8 - 13

1. 序論
　強磁性体の磁極（N極S極）は古代では方位磁針として使われ、近代からは電磁誘導を用いてエネルギー変換手法として利用されてきた。現代では磁極はハード磁気ディスクドライブに代表される磁気記録媒体として用いられている。一方で強磁性体を含有するスピントロニクスデバイスは磁極方向により電気抵抗を変える磁気抵抗効果を示す。従って磁極の方向を高効率に電気制御できれば、省エネルギーメモリデバイスとして応用できる。2000年にスピン流磁化反転が実証され^[1][1] J. A. Katine, F. J. Albert, R. A. Buhrman, E. B. Myers and D. C. Ralph: Phys. Rev. Lett. 84 (2000) 3149.、電磁誘導を用いずに電気的に直接磁極方向を変えられるようになった。このスピン流磁化反転は電磁誘導よりスケーリングに優れ、磁気メモリMRAM（magnetic random access memory）の駆動原理として期待されている^[2][2] K. Ando, S. Fujita, J. Ito, S. Yuasa, Y. Suzuki, Y. Nakatani, T. Miyazaki and H. Yoda: J. Appl. Phys. 115 (2014) 172607.。しかし、スピン流磁化反転も電流を必要とし、磁化反転に必要な最小エネルギー（Landauer限界）の10,000,000倍以上のエネルギーを消費する。そこで最近は電流を流さず、電圧をかけて強磁性体表面を帯電させるだけで磁化を反転する研究が行われている。この電圧磁化制御法の一つが電圧誘起磁気異方性変化である^[3-5][3] D. Chiba, M. Yamanouchi, F. Matsukura and H. Ohno: Science 301 (2003) 943-945.
[4] M. Weisheit, S. Fähler, A. Marty, Y. Souche, C. Poinsignon and D. Givord: Science 315 (2007) 349-351.
[5] T. Maruyama, Y. Shiota, T. Nozaki, K. Ohta, N. Toda, M. Mizuguchi, A. A. Tulapurkar, T. Shinjo, M. Shiraishi, S. Mizukami, Y. Ando and Y. Suzuki: Nat. Nanotechnol. 4 (2009) 158-161.。特にFeやCoを用いる強磁性金属薄膜の電圧誘起磁気異方性変化^[4,5][4] M. Weisheit, S. Fähler, A. Marty, Y. Souche, C. Poinsignon and D. Givord: Science 315 (2007) 349-351.
[5] T. Maruyama, Y. Shiota, T. Nozaki, K. Ohta, N. Toda, M. Mizuguchi, A. A. Tulapurkar, T. Shinjo, M. Shiraishi, S. Mizukami, Y. Ando and Y. Suzuki: Nat. Nanotechnol. 4 (2009) 158-161.は室温で生じるため、スピントロニクスデバイスの新たな駆動原理として注目されている。
　強磁性金属薄膜の電界誘起磁気異方性変化は、2007年に電解液に浸した厚さ数nmのFePt及びFePd薄膜で発見され^[2][2] K. Ando, S. Fujita, J. Ito, S. Yuasa, Y. Suzuki, Y. Nakatani, T. Miyazaki and H. Yoda: J. Appl. Phys. 115 (2014) 172607.、その後Fe/MgO等の室温固体素子における実証により脚光を浴びた^[3][3] D. Chiba, M. Yamanouchi, F. Matsukura and H. Ohno: Science 301 (2003) 943-945.。これまでに報告されている電圧効果には2種類ある。一つは金属と誘電体界面近傍での酸素イオンの移動に由来する電気化学反応である。この電圧誘起酸化還元反応は、FeCoO_x/MgO接合で発見され^[6][6] F. Bonell, Y. T. Takahashi, D. D. Lam, S. Yoshida, Y. Shiota, S. Miwa, T. Nakamura and Y. Suzuki: Appl. Phys. Lett. 102 (2013) 152401.、その後、Fe/BaTiO₃接合^[7][7] G. Radaelli, D. Petti, E. Plekhanov, I. Fina, P. Torelli, B. R. Salles, M. Cantoni, C. Rinaldi, D. Gutiérrez, G. Panaccione, M. Varela, S. Picozzi, J. Fontcuberta and R. Bertacco: Nat. Commun. 5 (2014) 3404.やFePt/イオンゲル接合^[8][8] K. Leistner, J. Wunderwald, N. Lange, S. Oswald, M. Richter, H. Zhang, L. Schultz and S. Fähler: Phys. Rev. B 87 (2013) 224411.で同様の効果が見出された。特にイオン伝導度の大きな誘電体を用いたCo/Gd₂O₃接合^[9,10][9] C. Bi, Y. Liu, T. Newhouse-Illige, M. Xu, M. Rosales, J. W. Freeland, O. Mryasov, S. Zhang, S. G. E. Velthuis and W. G. Wang: Phys. Rev. Lett. 113 (2014) 267202.
[10] U. Bauer, L. Yao, A. J. Tan, P. Agrawal, S. Emori, H. L. Tuller, S. Dijken and G. S. D. Beach: Nat. Mater. 14 (2015) 174-181.ではより顕著な電圧誘起酸化還元反応が起き、単位電界辺りの界面磁気異方性エネルギー（電圧誘起磁気異方性変化の大きさ）は、10,000 fJ/m²÷V/mを超える。もう一つは純粋に強磁性金属表面の電荷増減及び再配列で生じる効果^[11][11] S. Miwa, K. Matsuda, K. Tanaka, Y. Kotani, M. Goto, T. Nakamura and Y. Suzuki: Appl. Phys. Lett. 107 (2015) 162402.である。後者の電圧誘起磁気異方性変化は高々100 fJ/Vmであり、前者と比べて小さな値が報告されている。
　2種類の電圧効果のうち、前者の電気化学反応は大きな効果が魅力的であるものの、化学反応であるため熱活性過程が必要である。従って動作速度がサブミリ秒と遅く、メモリ動作に必要な繰り返し動作耐性を担保できない。一方で後者の電界効果はサブナノ秒以下の高速応答性^[12-15][12] Y. Shiota, T. Nozaki, F. Bonell, S. Murakami, T. Shinjo and Y. Suzuki: Nat. Mater. 11 (2012) 39-43.
[13] S. Kanai, M. Yamanouchi, S. Ikeda, Y. Nakatani, F. Matsukura and H. Ohno: Appl. Phys. Lett. 101 (2012) 122403.
[14] T. Nozaki, Y. Shiota, S. Miwa, S. Murakami, F. Bonell, S. Ishibashi, H. Kubota, K. Yakushiji, T. Saruya, A. Fukushima, S. Yuasa, T. Shinjo and Y. Suzuki: Nat. Phys. 8 (2012) 491-496.
[15] E. Tamura, J. van Ek, M. Fröba and J. Wong: Phys. Rev. Lett. 74 (1995) 4899.及び繰り返し耐性を有する。従って後者の電圧効果を大きくすればMRAMをはじめとしたスピントロニクスデバイスの駆動原理として利用可能であり、スピン流磁化反転に替わる新規スピン操作方法になり得る。一方で、現在報告されている後者の電圧誘起磁気異方性変化は高々100 fJ/Vmであり、メインメモリ応用に必要な1,000 fJ/Vmより小さい。そこで本研究では放射光を用いたX線磁気円二色性分光（XMCD）実験を行い、後者の強磁性金属表面の電荷増減及び再配列で生じる電圧誘起磁気異方性変化の機構を明らかにし、巨大効果を示す新物質材料設計指針獲得を試みた。

2. 実験手法
　本研究では、Fe/MgO界面にPtを単原子層（0.2 nm）挿入したFe/Pt/MgO系を採用した。電圧誘起磁気異方性変化は電圧による界面磁気異方性エネルギーの変調である。界面磁気異方性はスピン軌道相互作用と密接な関係があるため、スピン軌道相互作用が大きな材料の利用が有望である。そこで単原子層のPtをFe/MgO界面に用意した。通常のPtは常磁性体であるが、本研究で用いた単原子層Ptは強磁性体のFeと接しているため、誘導磁気モーメントを有する強磁性体である。
　図1は素子構造及び実験概要である。fcc-Pd(001)下地の上に、L1₀-FePt(001)超薄膜を用意し、fcc-MgO(001)とポリイミド絶縁膜を通して外部から電界をPt/MgO界面に印加した。Pt L吸収端のXMCD分光では硬X線（10 keV超）を用いる。硬X線は比較的厚い誘電体を透過するため、X線照射面積を大きく取るためにMgO（5 nm）とポリイミド（1,500 nm）の2層誘電体を用いた。実験ではPt/MgO界面を有するL1₀-FePt(001)/fcc-MgO(001)接合を用いた。FePtはFe原子層（0.14 nm）とPt原子層（0.20 nm）を交互に電子線蒸着法で積層させて成膜した。図1の電子顕微鏡写真において白く輝く原子がPtであり、MgOとの界面に確かに1原子層のPtが存在することがわかる。本研究の参照実験としてPt/MgO界面を有するFePt/MgOとFe/MgO界面を有するFePt/MgO、それぞれの電圧誘起磁気異方性変化を評価した。結果としてFe/Pt/MgO系はFe/MgO系の30 fJ/Vm^[11][11] S. Miwa, K. Matsuda, K. Tanaka, Y. Kotani, M. Goto, T. Nakamura and Y. Suzuki: Appl. Phys. Lett. 107 (2015) 162402.よりも大きな140 fJ/Vmの電圧磁気異方性変化を示すことがわかった。

図1　素子構造及び実験概要

3. 結果と考察
　FePt/MgO接合の電圧磁気異方変化をPt-L₃吸収端のXMCD信号で評価した（図2）。図2の横軸は膜面垂直方向の外部磁場強度、縦軸はPt-L₃吸収端のXMCD強度である。XMCD強度は膜面垂直方向の磁化の大きさに比例する。このグラフから負電圧下の磁化曲線は磁場掃引方向で結果が異なるヒステリシスを示すのに対し、正電圧下の磁化曲線ではヒステリシスが消失することがわかる。これはFePt/MgO膜の垂直磁気異方性が電圧で変化したことを意味する。なお、±200 VはMgO絶縁体中の±0.7 V/nmに相当する。電圧印加時にPt/MgO界面に電子が蓄積される方向を正電圧と定義した。

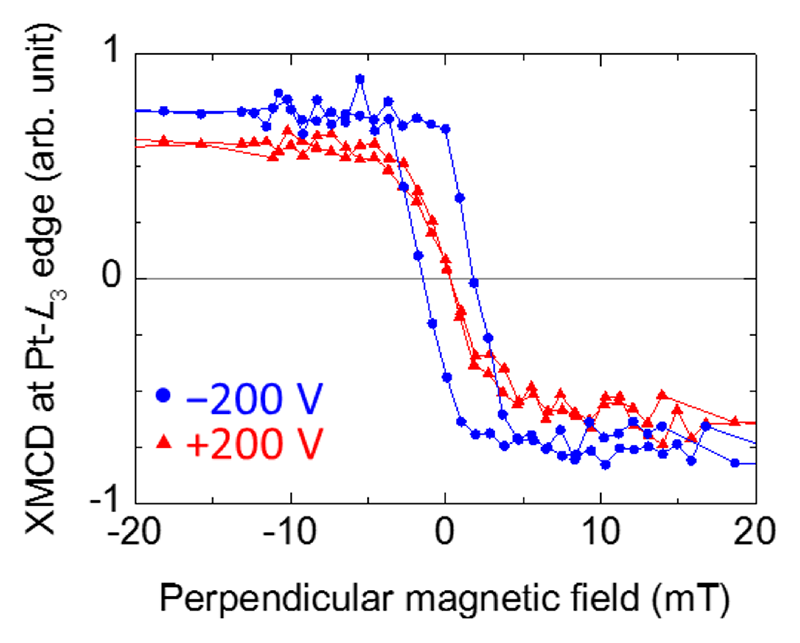
図2　Fe/Pt/MgO系の電圧磁気異方性変化

　Pt吸収端のX線吸収（XAS）及びXMCDスペクトルを図3に示す。±200 Vの外部電圧下で測定し、それぞれ赤及び青で示した。実験中は外部磁場60 mTを膜面垂直に印加し、磁化を飽和させている。XAS differenceは、−200 VのXASから、+200 VのXAS信号を差し引いたものである。XAS differenceを注視すると、外部電圧によりPtの電子状態が変化していることがわかる。例えば黒矢印は2pから5dへの遷移に相当する。選択則からL₃端遷移は2p_3/2 → 5d_3/2及び2p_3/2 → 5d_5/2を含むのに対し、L₂端遷移は2p_1/2 → 5d_3/2を含むことがわかる。XAS differenceの黒矢印部分はL₃端でのみ顕著であるため、負電圧が5d_5/2準位の電子を欠乏させ、空状態の状態密度を大きくしたと考えられる。Ptに電界を印加すると静電遮蔽によりPt原子の電子は欠乏するため、5d軌道の電子欠乏はこのことと一致する。なお赤矢印は2pから6sへの遷移を示す^[15][15] E. Tamura, J. van Ek, M. Fröba and J. Wong: Phys. Rev. Lett. 74 (1995) 4899.。実験結果からは5d軌道と異なり6s軌道には電子が充填されていることがわかる。これはPt原子が静電遮蔽を起こすために電気双極子をs-p混成軌道から生成し、結果としてp軌道からs軌道に電子が移動するためであると考えられる。XMCD integralは実験的に得たXMCDスペクトルの数値積分である。負電圧を印加するとL₃端L₂端ともにXMCD信号強度が増大することがわかった。

図3　Pt吸収端でのXMCD分光結果

　XMCDのスペクトルの強度を解析すると、磁気モーメントの情報を得られることが知られている。これをサムルール解析^[16,17][16] B. T. Thole, P. Carra, F. Sette and G. van der Laan: Phys. Rev. Lett. 68 (1992) 1943.
[17] P. Carra, B. T. Thole, M. Altarelli and X. Wang: Phys. Rev. Lett. 70 (1993) 694.というが、本研究でもこの解析によりPtの磁気モーメント及び磁気モーメントの電圧変化を求めた。電圧を印加しない時、Pt原子における垂直磁場下の有効スピン磁気モーメント（m_eff = m_S – 7m_T）は0.30 µ_B、軌道磁気モーメント（m_L）は0.055 µ_B、5d軌道のホール数（n_5d）は1.76であった。ここでm_S、m_T、µ_Bはそれぞれスピン磁気モーメント、電気四極子並びに原子内部のスピン密度非対称性と関連する磁気双極子モーメント、ボーア磁子である。各磁気モーメントは、m_S = −2 µ_B<S_α>/ħ、m_L = −µ_B<L_α>/ħ、m_T = µ_B<T_α>/ħの関係を持つ。<S_α>、<L_α>、<T_α>はスピン角運動量、軌道角運動量、磁気双極子演算子のα方向成分期待値である。スピン軌道相互作用が<T_α>に及ぼす影響を無視できる時、磁気双極子演算子は、T = S – 3r(r∙S)～−2Q∙S/7と記述できる。ここでrとQは位置ベクトル及び電気四重極子テンソルである。系がC_4v対称性を有する系の場合、Tは単純に式1で表される。

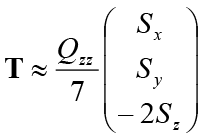･････（1）

z方向を膜面垂直方向とした。
　次に電圧による磁気モーメント及びホール数の変化を議論したい。負電圧印加時の有効スピン磁気モーメントは正電圧印加時のそれと比較すると13％増大することがわかった。一方で軌道磁気モーメントの変化量は観測限界以下（< 7％）であった。一方でホール数は正電圧を印加すると0.019（～1％）増大した。有効スピン磁気モーメントの変化量（13％）はホール数の変化量（1％）よりも非常に大きく、Ptの価電子数を大きく変える電気化学反応ではなく純粋にPt原子の磁性を担う5d軌道の電子再配列により有効スピン磁気モーメントの変化が起きていることがわかる。
　有効スピン磁気モーメント（m_eff）はスピン磁気モーメント（m_S）とm_T項の和である。一般的に正方晶・界面・薄膜等の対称性が低い系では原子の電子分布は電気四極子を有する。この時、電子がスピン偏極していると電気四重極子は原子内部のスピン分布異方性を与える。これがm_T項である^[18][18] G. van der Laan: J. Phys: Condens. Matter. 10 (1998) 3239.。式1からm_T項に磁化角度依存性があることがわかる。一方でスピン磁気モーメントは磁化方向に依存しない。我々の実験では電圧をかけない状態ではm_T項がほぼゼロであった（< 0.01 µ_B）。一方で負電圧を印加すると正のm_T項が発現した。そしてm_T項の電圧誘起は垂直磁化でのみ顕著であった。これらのことから、13％もの有効スピン磁気モーメントの増大は主にm_T項に由来すると結論できる。我々の検討結果はm_effの電圧変化量における70％以上がm_Sでなくm_Tに起因することを示している。
　次にこのFePt/MgO系の磁気異方性及び磁気異方性変化の起源を議論する。磁気異方性エネルギーをl∙sカップリングのスピン軌道相互作用係数に対する2次摂動で考えると式2で表される^[18][18] G. van der Laan: J. Phys: Condens. Matter. 10 (1998) 3239.。

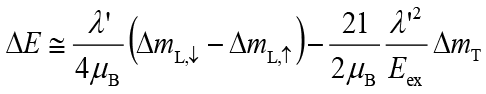･････（2）

　垂直磁気異方性エネルギー（ΔE）の定義は垂直磁化と面内磁化の磁気異方性エネルギー差である。λ'はdバンドの有効スピン軌道相互作用係数である。Δm_L,↓(↑)は少数（多数）スピンバンド由来の軌道磁気モーメントの磁化角度異方性（垂直磁化と面内磁化の差）である。なお、測定で得られる軌道磁気モーメントはm_L = m_L,↓ + m_L,↑であり、注意が必要である。式2の第一項は軌道磁気モーメント由来の磁気異方性である。多数スピンバンドが埋まると仮定してm_L,↑を無視すると垂直磁気異方性エネルギーはm_Lに比例し、表面界面磁性の分野で著名なBrunoの式と一致する^[19][19] P. Bruno: Phys. Rev. B 39 (1989) 865(R).。しかし、Ptは交換相互作用がFeやCo等の3d遷移金属強磁性体と比べて小さく、m_L,↑を無視できない。第二項はm_T項由来の磁気異方性である^[18][18] G. van der Laan: J. Phys: Condens. Matter. 10 (1998) 3239.。これは交換相互作用（E_ex）で分離された多数スピンバンドと少数スピンバンド間のスピン反転励起過程に起因する。従って大きなλ'及び小さなE_exの時に有限な値を持つ。本研究のように5d遷移金属のPtはこの条件を満たす。
　次に第一原理計算による検討を行った。計算では、式2において「（第一項）:（第二項）= −0.91 : 1.00」であることがわかった。これは第二項の寄与が大きいこと、そして実験で得た電圧誘起磁気異方性変化140 fJ/Vmは第一項と第二項が相殺され、第二項の寄与が一部残った結果であることがわかる。従って2つの機構の寄与を調節すれば応用レベルの1,000 fJ/Vmを超える巨大電圧効果を現実的に得る可能性が十分にあることがわかった。
　最後に電圧磁気異方性変化の物理描像を説明したい。強磁性金属の電界誘起磁気異方性変化は前述の式2で表せる。式2の第一項はl∙sカップリングのl_zs_z項由来のエネルギーとも言える。これはl∙sカップリングをスピンが保存した波動関数で挟んだ時に得られるエネルギーである。別の言い方をすると電界により金属原子の電子数が変化し、その結果として軌道磁気（双極子）モーメントが発生した結果である（図4上図）。一方で式2の第二項はl∙sカップリングの（l₊s₋ + l₋s₊）項由来のエネルギーである。これはl∙sカップリングをスピンが反転した波動関数で挟んだ時に得られるエネルギーであり、電界により金属原子の電子雲が歪んで（電子の再配列が起きて）電気四極子が発生し、結果として磁気モーメント分布が異方的になった結果であると言える（図4下図）。

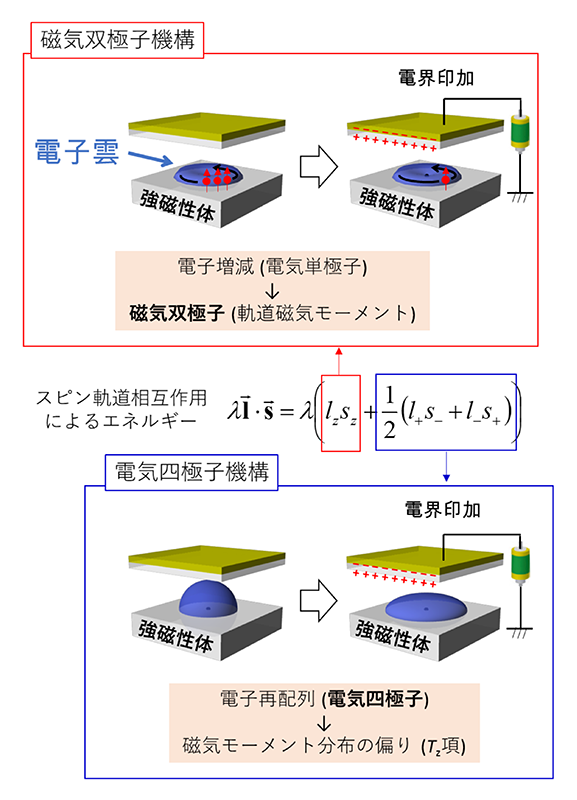
図4　電圧磁気異方性変化の機構

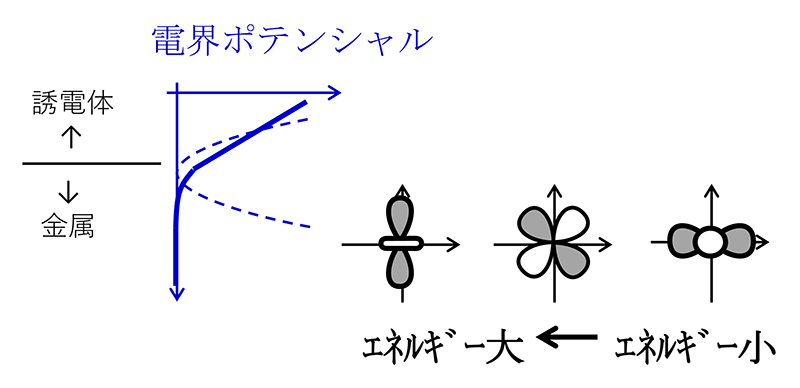
図5　電気四極子の発生原理

4. 結論
　本研究では良質なFePt/MgO接合デバイスを作製してXMCD分光を行い、電圧誘起磁気異方性変化の機構解明を目指した。結果として電界によりPt原子に電気四極子が発生し、T_z項の変化が生じることを実験的に見出した。本研究により電圧誘起磁気異方性変化の描像が明らかになり、今後の電圧スピントロニクスデバイスの材料研究の指針が明確になった。本研究の詳細は文献[20]に記載されている。

謝辞
　本研究は大阪大学のFrédéric Bonell氏、松田健彰氏、塚原拓也氏、鈴木義茂氏、縄岡孝平氏、後藤穣氏、産業技術総合研究所の野崎隆行氏、湯浅新治氏、高輝度光科学研究センターの鈴木基寛氏、中村哲也氏、小谷佳範氏、そして東北大学の辻川雅人氏、白井正文氏らとの共同研究成果である。そして本研究の一部は革新的研究開発推進プログラム（ImPACT）、科研費新学術領域研究「ナノスピン変換科学」及び若手研究（A）の支援により行われた。XAS／XMCD測定はSPring-8のBL39XU及びBL25SUで行われた（課題番号2014B1007、2015A1003、2015A1572、2015B0079、2015B1020、2015B1250、2016A0079、2016A1122、2016A1314、2016B1017）。

参考文献
[1] J. A. Katine, F. J. Albert, R. A. Buhrman, E. B. Myers and D. C. Ralph: Phys. Rev. Lett. 84 (2000) 3149.
[2] K. Ando, S. Fujita, J. Ito, S. Yuasa, Y. Suzuki, Y. Nakatani, T. Miyazaki and H. Yoda: J. Appl. Phys. 115 (2014) 172607.
[3] D. Chiba, M. Yamanouchi, F. Matsukura and H. Ohno: Science 301 (2003) 943-945.
[4] M. Weisheit, S. Fähler, A. Marty, Y. Souche, C. Poinsignon and D. Givord: Science 315 (2007) 349-351.
[5] T. Maruyama, Y. Shiota, T. Nozaki, K. Ohta, N. Toda, M. Mizuguchi, A. A. Tulapurkar, T. Shinjo, M. Shiraishi, S. Mizukami, Y. Ando and Y. Suzuki: Nat. Nanotechnol. 4 (2009) 158-161.
[6] F. Bonell, Y. T. Takahashi, D. D. Lam, S. Yoshida, Y. Shiota, S. Miwa, T. Nakamura and Y. Suzuki: Appl. Phys. Lett. 102 (2013) 152401.
[7] G. Radaelli, D. Petti, E. Plekhanov, I. Fina, P. Torelli, B. R. Salles, M. Cantoni, C. Rinaldi, D. Gutiérrez, G. Panaccione, M. Varela, S. Picozzi, J. Fontcuberta and R. Bertacco: Nat. Commun. 5 (2014) 3404.
[8] K. Leistner, J. Wunderwald, N. Lange, S. Oswald, M. Richter, H. Zhang, L. Schultz and S. Fähler: Phys. Rev. B 87 (2013) 224411.
[9] C. Bi, Y. Liu, T. Newhouse-Illige, M. Xu, M. Rosales, J. W. Freeland, O. Mryasov, S. Zhang, S. G. E. Velthuis and W. G. Wang: Phys. Rev. Lett. 113 (2014) 267202.
[10] U. Bauer, L. Yao, A. J. Tan, P. Agrawal, S. Emori, H. L. Tuller, S. Dijken and G. S. D. Beach: Nat. Mater. 14 (2015) 174-181.
[11] S. Miwa, K. Matsuda, K. Tanaka, Y. Kotani, M. Goto, T. Nakamura and Y. Suzuki: Appl. Phys. Lett. 107 (2015) 162402.
[12] Y. Shiota, T. Nozaki, F. Bonell, S. Murakami, T. Shinjo and Y. Suzuki: Nat. Mater. 11 (2012) 39-43.
[13] S. Kanai, M. Yamanouchi, S. Ikeda, Y. Nakatani, F. Matsukura and H. Ohno: Appl. Phys. Lett. 101 (2012) 122403.
[14] T. Nozaki, Y. Shiota, S. Miwa, S. Murakami, F. Bonell, S. Ishibashi, H. Kubota, K. Yakushiji, T. Saruya, A. Fukushima, S. Yuasa, T. Shinjo and Y. Suzuki: Nat. Phys. 8 (2012) 491-496.
[15] E. Tamura, J. van Ek, M. Fröba and J. Wong: Phys. Rev. Lett. 74 (1995) 4899.
[16] B. T. Thole, P. Carra, F. Sette and G. van der Laan: Phys. Rev. Lett. 68 (1992) 1943.
[17] P. Carra, B. T. Thole, M. Altarelli and X. Wang: Phys. Rev. Lett. 70 (1993) 694.
[18] G. van der Laan: J. Phys: Condens. Matter. 10 (1998) 3239.
[19] P. Bruno: Phys. Rev. B 39 (1989) 865(R).
[20] S. Miwa, M. Suzuki, M. Tsujikawa, K. Matsuda, T. Nozaki, K. Tanaka, T. Tsukahara, K. Nawaoka, M. Goto, Y. Kotani, T. Ohkubo, F. Bonell, E. Tamura, K. Hono, T. Nakamura, M. Shirai, S. Yuasa and Y. Suzuki: Nat. Commun. 8 (2017) 15848.

三輪　真嗣　MIWA Shinji
大阪大学　大学院基礎工学研究科
〒560-8531　大阪府豊中市待兼山町1-3
TEL : 06-6850-6426
e-mail : miwa@mp.es.osaka-u.ac.jp