Volume 22, No.2 Pages 91 - 98

1. はじめに
　凝集系にはミクロからマクロな空間スケールにわたって階層構造を有するものが多く存在し、その階層構造がマクロな物性や機能の発現において重要な役割を担うことがある。構造の階層性に関してこれまで非常に多くの研究がなされてきた。可視レーザー光、X線、中性子、電子などをプローブとして用いることで、原子スケールからマクロな長さスケールにわたる広い空間スケールにおいて物質の構造を調べることが可能であり、物質の構造の理解に飛躍的な進展がもたらされてきた。物質中の多様な振動・緩和ダイナミクスを調べるためには、赤外分光法、ラマン分光法、各種ブリルアン散乱測定法、可視光光子相関法など、様々な測定法が用いられている。これらの手法ではダイナミクスの時間スケールに関する知見は得られるが、ミクロな空間スケールに関する情報は乏しい。しかしながら、物質の機能や物性をより詳細に理解するためには時間スケールのみならず、ダイナミクスのミクロな空間スケールに関する理解も必要である。
　ミクロな空間スケールにおいて各時間スケールの物質のダイナミクスを測定する手法として、中性子やX線の非弾性・準弾性散乱法や中性子スピン・エコー法、X線光子相関法などが挙げられる。それらの手法は、それぞれユニークな時間・空間スケールをカバーしている。図1に様々な手法がカバーする典型的な空間・時間領域を示す^[1][1] 齋藤真器名：固体物理 47 (2012) 11.。

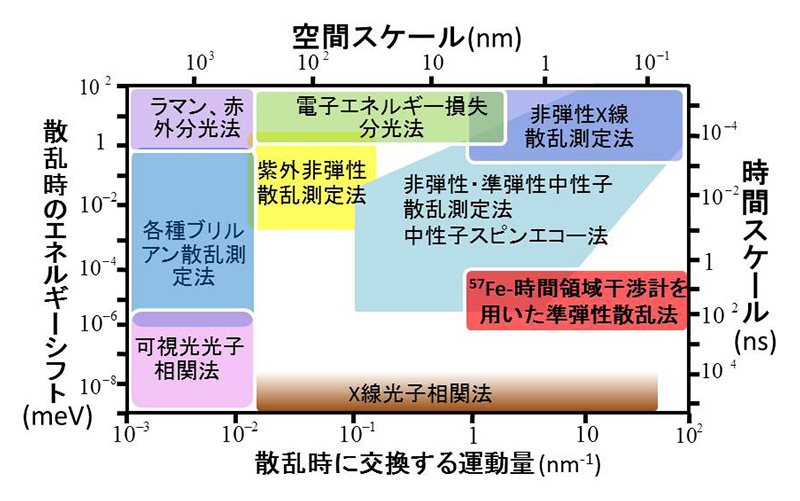
図1　様々なエネルギー・時間分解能を有する非弾性・準弾性散乱法とそれらのカバーするダイナミクスの時間・空間スケール

　凝縮系において重要となるダイナミクスの時間スケールは、一般にフェムト秒～マクロな時間スケールと非常に幅が広く、図1に示されているように現状では1つの方法ではすべての時間・空間スケールをカバーすることができない。図1中の“⁵⁷Fe−時間領域干渉計を用いた準弾性散乱法”の示す領域は、本稿で解説する時間領域干渉計を用いたガンマ線準弾性散乱法のカバーする時間・空間領域である。時間領域干渉計を用いたガンマ線準弾性散乱法により、他の手法では測定が非常に困難な原子・分子スケールの数ns～サブµsの時間スケールのダイナミクスを測定できる。この時間スケールは、結晶固体と液体の中間にあるような半固体的な物質中で原子・分子が運動する時間スケールとなっている。そのような時間スケールのミクロなダイナミクスを理解することは、基礎物性研究においてはもちろん、様々な産業利用材料（例えばイオン伝導ガラス、イオン液体、液晶、脂質膜、ゴムなど）や生体系のモデル物質においても大変重要であることが近年分かってきており、現在精力的に研究されている。本稿ではその原理と応用例に加えて、なぜ本手法がセベラルバンチモードを必要とするかを解説する。
　2章ではまず準弾性散乱実験の基礎として、試料がない場合に、放射光により励起された原子核が放射するガンマ線の前方散乱時間スペクトルがどのように観測されるか、そして、2つの異なる励起エネルギーをもつ原子核からガンマ線が放射される場合に、時間領域上でどのようにそれらが干渉し、いかにガンマ線のエネルギープロファイルと対応付けられるかを解説する。3章では、一般的なモノクロメーター、アナライザーを用いたエネルギー領域上での非弾性・準弾性散乱実験の基礎を解説する。4章以降では、時間領域干渉計を用いた準弾性散乱について解説する。本手法、“時間領域干渉計を用いた準弾性散乱法”は、時間領域においてダイナミクスを測定する方法であるが、エネルギー領域上の測定と同等な情報を得ることができることを説明する。本手法を一言で言えば、レーザーを用いた実験手法の光ヘテロダイン干渉法と同様に、プローブ・リファレンス光を時間領域上で干渉させ、その干渉パターンからダイナミクスの情報を引き出す手法である。時間領域干渉計のセットアップでは、2章で解説した2つの異なる励起エネルギーをもつ原子核から放射されるガンマ線を、それぞれプローブ・リファレンスガンマ線として用いる。プローブ・リファレンスガンマ線としてそれぞれに単一のエネルギーのガンマ線を用いる場合が、基本となる“シングルラインの時間領域干渉計”という手法である。このシングルラインの時間領域干渉計については4章で解説する。測定の効率を上げるために、プローブ・リファレンスそれぞれに複数エネルギーのガンマ線を用いるのが、“マルチラインの時間領域干渉計”であり、5章ではその原理を解説する。6章では、時間領域干渉計を用いた準弾性散乱実験のこれまでの応用結果を紹介し、7章では他の準弾性散乱法との関係性をさらに詳細に議論し、まとめと今後の展開を最後に述べる。

2. 核共鳴（ガンマ線）前方散乱^[2,3][2] 瀬戸誠：日本結晶学会誌 43 (2001) 405-412.
[3] 瀬戸誠：固体物理 44 (2009) 27.
　この章では、準弾性散乱実験でプローブ、リファレンスとして用いられるガンマ線吸収体1、2からの放射ガンマ線が、試料がない場合にどのように時間領域上で干渉するのかを解説し、それらのエネルギースペクトルとの関係性を明らかにする。
　ガンマ線を用いた準弾性散乱実験の基礎となる、⁵⁷Fe核共鳴前方散乱実験のセットアップを図2(a)に示す。SPring-8などの大型放射光施設において、電子は高周波バケット内の安定な領域で集団（バンチ）を形成し、蓄積リングを周回することで放射光を出す。ここで、蓄積リング内で電子がどのような構造のバンチを形成するかは放射光運転のバンチモードに依存するが、例えば、Dモード（1/7-filling ＋ 5 bunches）では、図2(a)に示されるようなバンチが比較的連続的に連なったマルチバンチ部と、1バンチが孤立したシングルバンチからなるバンチ構造を有する。シングルバンチ部の電子から放射される放射光は時間幅数十psのパルスとみなせる。⁵⁷Fe核の前方散乱実験では、このような放射光のエネルギーを⁵⁷Fe原子核の核励起エネルギー～14.4 keV近傍でmeV程度の幅に分光する。この放射光を、相対的に核励起エネルギー差δEをつけた2つの⁵⁷Feガンマ線放射体を通過させ、前方方向の散乱強度の時間依存性測定、すなわち時間スペクトル測定を行う。核励起エネルギー差をつける方法としては、同等な2つの⁵⁷Fe放射体間に相対速度を与えることで、ドップラー効果により両者の核励起エネルギーを相対的に変化させるなどの方法がある。検出器としては1 nsの時間分解能を有するアヴァランシェフォトダイオード検出器（APD）を用いる。

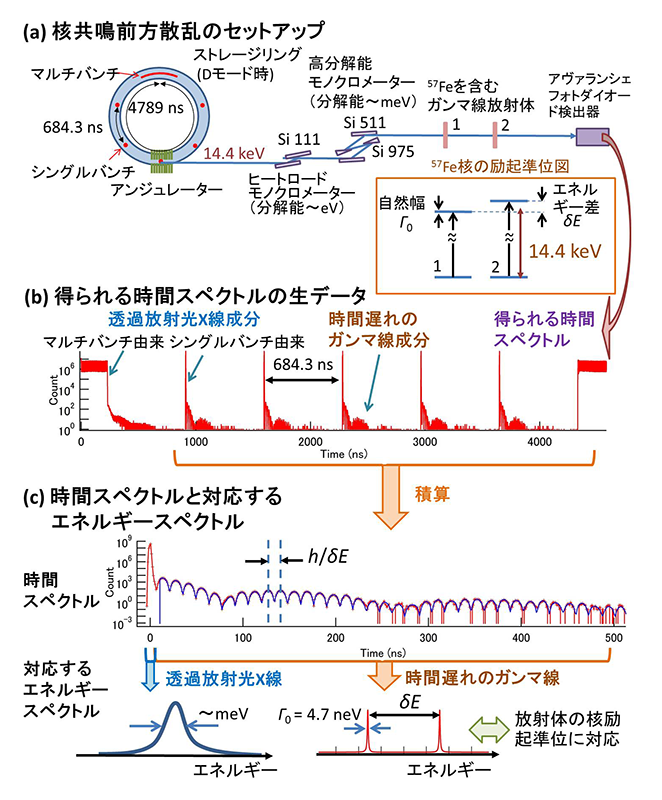
図2　核共鳴前方散乱測定の、(a) セットアップ（Dモード運転時、BL09XU、SPirng-8での測定の例）、(b) 得られる時間スペクトルの生データと、(c) 積算されて得られた時間スペクトルと対応するエネルギースペクトルの概念図

　パルス放射光により原子核が励起された場合、励起原子核は励起寿命（⁵⁷Fe原子核の場合141 ns）程度の時間スケールでガンマ線を放射し基底状態に戻る。励起核から弾性的に放射されたガンマ線は核の励起エネルギーを有する、共鳴エネルギー幅Γ₀～4.7 neV程度のエネルギー不確定幅を持つ単色の光であり、入射パルスに対し励起核の寿命程度遅れて検出される。このような単色ガンマ線には、入射光の向きと指向性を比較的保ったまま放射される成分があり、前方方向ではそのような指向性を保った弾性成分が主として観測される。“核共鳴散乱”は、励起原子核から放射される散乱（電子、蛍光X線、弾性・非弾性ガンマ線など）の総称であるが、本研究ではこの弾性的で前方方向に指向性をもって放射されるガンマ線が重要な役割を果たす。以降このようなガンマ線を単にガンマ線と呼ぶ。
　このような前方散乱実験において、蓄積リングの周回時間4789 nsにわたって繰り返し積算された時間スペクトルを図2(b)に示す。マルチバンチおよびシングルバンチ由来の透過放射光として示された比較的高強度の成分は、蓄積リングのバンチ構造をそのまま反映したものとなっている。一方、それらに対し原子核の励起寿命の時間スケールだけ遅れてガンマ線成分が観測される。図2(c)にシングルバンチ部のスペクトルを5つ分積算して得られた時間スペクトルを示す。得られた時間スペクトル上には、2つのガンマ線放射体のエネルギー差δEから決まる周期h/δEのうなり（量子ビート）が観測される。核共鳴前方散乱実験では、このような時間スペクトル上の量子ビートの周期から核の励起エネルギーの差などを決定することができる。
　この量子ビートは一見すると特異な現象に見えるが、放射光ユーザーにとって馴染み深い、位置−運動量空間における回折実験と共通点を見出すことができる。回折実験において、位置−運動量空間は互いにフーリエ変化により関係付けられ、X線回折測定により運動量空間上での回折プロファイルから原子位置の情報を得ることができる。一方、エネルギー（または角振動数）と時間も同様にフーリエ変換の関係性にあり、回折実験で位置をエネルギー、運動量を時間と読み替えると、量子ビートは、異なったエネルギーを有する光子が時間領域上でつくる干渉縞と例えることができる。どのような時間スケールまで干渉縞ができるかはガンマ線の単色性が決めており^[4][4] 菊田惺志：X線散乱と放射光科学 基礎編（東京大学出版会、2011）、neVレベルまで単色なガンマ線を用いることで、ようやく比較的高速の検出器であるAPDを用いて、実験的に測定可能な100 nsの時間スケールで干渉縞を観測することができる。そのため、時間領域上での干渉は、物理現象としては一般的な現象にもかかわらず、多くの放射光実験では馴染みのないものになっている。
　回折実験においては、運動量空間での回折プロファイルが散乱体位置の情報を有し、広い運動量空間で測定を行うことで、精度よく位置に関する情報を得ることができる。同様に、時間領域上での干渉縞である量子ビートは、ガンマ線のエネルギー情報を有し、時間スペクトルを広い時間スケールで測定することによって詳細なエネルギーの情報を引き出すことができる。時間スケールの幅を広くとるために、核共鳴前方散乱実験では、パルス間隔が適当に開いた運転モードであるセベラルバンチモードが必要となっている。また後述するように、時間領域干渉計を用いた準弾性散乱実験でも測定したいダイナミクスの時間領域を含む広い時間スケールにわたって時間スペクトルを観測する必要があるため、長いパルス間隔のセベラルバンチモード、例えばSPring-8の場合にはD（684.3 ns）、およびF（342 ns）モードの利用が大変有利となる。ここで、括弧内の数字はシングルバンチとシングルバンチの間隔である（さらに詳細な解説は文献2、3を参照）。

3. 非弾性・準弾性散乱の典型的な測定手段^[5,6][5] 細川伸也：分光研究 57 (2008) 301-312.
[6] A. Q. R. Baron：固体物理 44 (2009) 11.
　時間領域干渉計の解説の前に典型的な非弾性・準弾性散乱実験について解説する。エネルギー領域上での準弾性散乱実験としては、比較的エネルギー不確定幅の狭い光などの粒子を拡散などのダイナミクスを調べたい試料に照射し、散乱粒子のエネルギースペクトルを調べる実験を行う。このとき、試料中のミクロな運動性に応じて試料と散乱粒子はエネルギーを移行し合う。これにより散乱粒子のエネルギーの幅は広がるなど変化するため、その変化から試料のダイナミクスを調べることができる。非弾性・準弾性散乱法は、プローブ粒子のエネルギーや散乱角などを選択することにより試料との運動量移行qを変化させることで、ダイナミクスを調べたい試料の空間スケールを選択できるという特徴がある。この特性により、例えば複雑な構造をもつ物質においても、その内部で異なる空間スケールでのダイナミクスを比較的独立に調べることができる。図3に典型的な非弾性・準弾性散乱実験のセットアップの模式図を示す。試料上流側のモノクロメーターにより入射粒子のエネルギー幅をΔE_monoと制限しておく。試料より散乱された電場強度のエネルギープロファイルは、いわゆる動的構造因子S(q,E)（Eはエネルギー）が入射エネルギープロファイルに畳み込まれたような形をしている。動的構造因子は、X線を用いた場合、電子密度ρ(r,t)（rは位置ベクトル、tは時間）の時空間相関関数であるG(r,t)のrおよびtに関するフーリエ変換により定義されており、試料の詳細なダイナミクスの情報を有する（さらに詳細な解説は文献5、6を参照）。

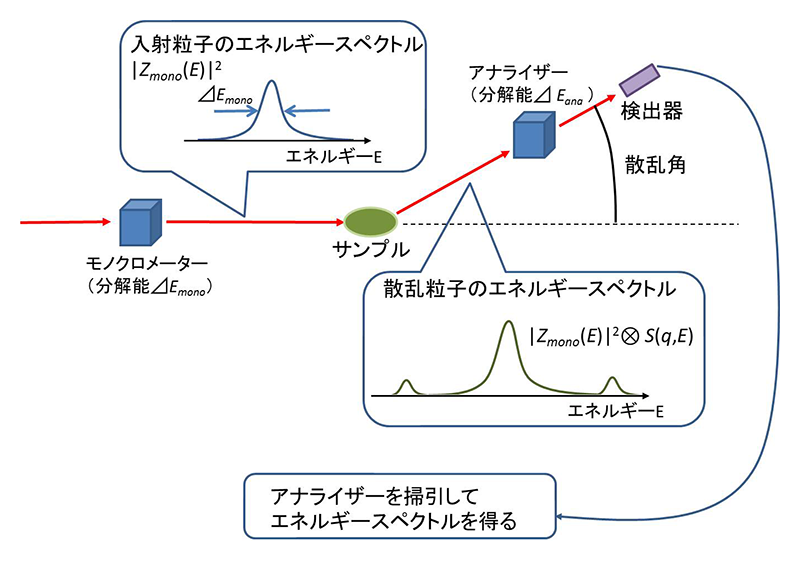
図3　典型的な非弾性・準弾性散乱実験のセットアップの概念図

　一般的にS(q,E)は広いエネルギー、qスケールにわたり物質の構造とダイナミクスを特徴付けるような形状を有する。観測可能なS(q,E)のエネルギースケールは測定系の分解能ΔE_mono、およびアナライザーの分解能ΔE_ana（典型的にはΔE_mono～ΔE_ana）の近傍となる。図1に示すように、例えばBL35XUで実験可能なX線非弾性散乱測定は、meVスケールのエネルギー分解能を有する測定系であり、これは、フーリエ変換すると、時間スケールps程度以上のダイナミクスの測定が可能となっていることに対応している。
　回折実験において測定するqレンジが大きいほど小さな構造を調べることができることに対応して、一般的にエネルギー分解能が高い測定系ほどより長い時間スケールのダイナミクスの測定に適している。⁵⁷Fe核からのガンマ線は数neVの分解能を有しているので、X線非弾性散乱測定の数100000倍ほど長い時間スケール（100 ns）のダイナミクス測定が可能となる。

4. シングルラインの時間領域干渉計^[7-9][7] A. Q. R. Baron et al.: Phys. Rev. Lett. 79 (1997) 2823.
[8] G. V. Smirnov, V. G. Kohn and W. Petry: Phys. Rev. B 63 (2001) 144303.
[9] G. V. Smirnov et al.: Phys. Rev. B 73 (2006) 184126.
　⁵⁷Fe核からのガンマ線を用いた時間領域干渉計のセットアップの概念図を図4に示す。実験はSPring-8、BL09XUにおいて行っている。この図では、4.7 neVのエネルギー不確定幅を有する単一の励起エネルギーをもつシングルラインのガンマ線放射体を用いたセットアップを示している。ここでは、試料として、長周期構造のない物質（例えば液体）を考える。放射光のパス上の試料の前後にはガンマ線放射体1と2を配置し、前述の前方散乱実験と同様にそれらの励起エネルギーをδEだけ異なったものとしておく。

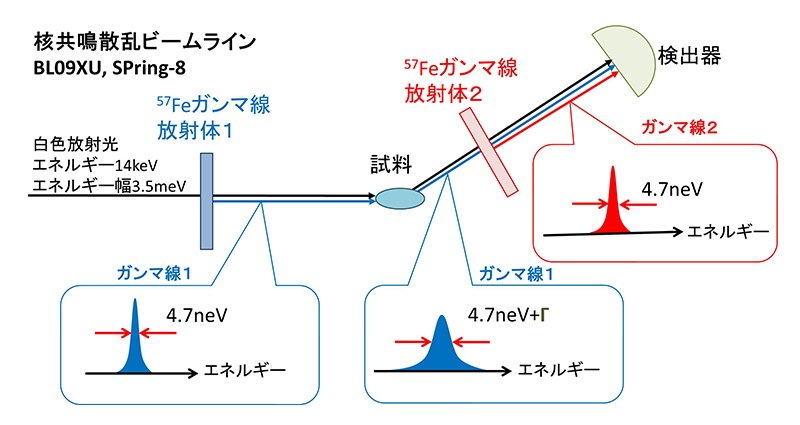
図4　ガンマ線準弾性散乱実験セットアップの概念

　3章では入射光を単色化することにより、散乱実験において試料の動的な応答をエネルギー領域上で観測する非弾性・準弾性散乱法を説明した。一方、放射光によりガンマ線を生成した場合は、単色なガンマ線成分以外に透過放射光成分も試料によって散乱されるため、上述のエネルギー領域上の測定をそのまま行うことができない（例えば、⁵⁷Feの核共鳴を用いた場合、透過成分はそれに対し100000倍ほど強い）。ここで、前方散乱実験でガンマ線の時間スペクトル測定をすると、強い透過放射光成分とガンマ線を分けて観測でき、しかも時間スペクトル上の量子ビートからガンマ線のエネルギースペクトルの情報が得られることを利用すると、ガンマ線を用いた準弾性散乱実験においても、時間スペクトルを測定し量子ビートを調べることで、S(q,E)を得ることができると考えられる。S(q,E)がどのように量子ビートに影響するか調べるため、まずは図4を基に試料での散乱過程によるガンマ線のエネルギープロファイルの変化を考える。放射体1から放射されたガンマ線1が試料により準弾性散乱されると、エネルギー幅は、試料中の拡散の度合い（すなわちS(q,E)）に応じて半値全幅Γ分だけ広がる。ガンマ線1はプローブ光として機能する。一方、試料の下流側にあるガンマ線放射体2から放射されるガンマ線2については、そのエネルギー幅は試料による準弾性散乱による広がりを受けない。そのため、ガンマ線2はリファレンス光として機能する。原子核共鳴を起こさない大部分の放射光に対し、時間的に遅れてこれら2つの放射体起源のガンマ線が検出器に到着することになる。
　S(q,E)の中心ピークの幅Γが、neVのエネルギースケールに比べて十分狭い場合、前方散乱の条件とほぼ変わらなくなる。ゆえに、図5(a)のように時間領域上の量子ビートは比較的明瞭なものとなる。一方、拡散が速くなると図5(b)のようにガンマ線1のエネルギー幅が広がるため、時間領域上で量子ビートの振動数成分が増え、量子ビートが時間とともに緩和するような効果をもたらす。より一般的には、量子ビートは、S(q,E)の時間領域上の表現である関数S(q,t)に従って緩和することを示すことができる。このS(q,t)を中間散乱関数と呼ぶ。中性子スピン・エコー法やX線光子相関法も、時間領域上でダイナミクスを測定し、S(q,t)を求める手法である。このように、時間スペクトルの測定を通じて量子ビートの明瞭性の時間変化を調べることにより、試料のミクロなダイナミクスを調べることができる。

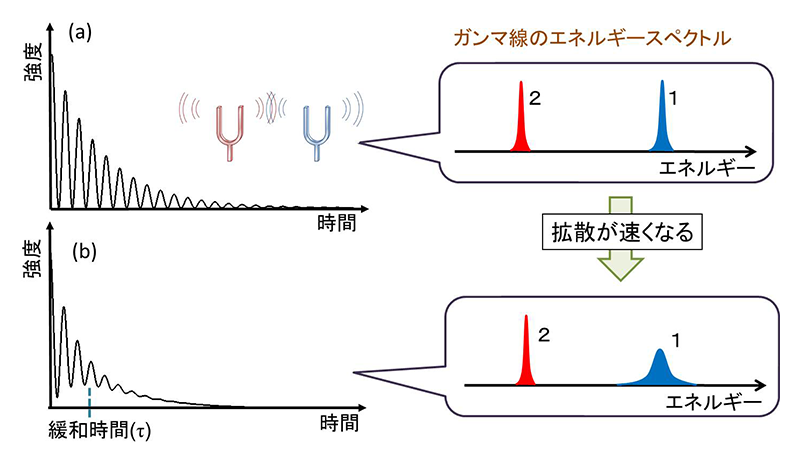
図5　ダイナミクスが比較的、(a) 早い場合と、(b) 遅い場合のシングルラインの時間領域干渉計の時間スペクトルと対応するガンマ線のエネルギースペクトル

5. マルチラインの時間領域干渉計^[10][10] M. Saito et al.: Hyperfine Interact. 206 (2012) 87-90.
　シングルラインのガンマ線準弾性散乱法では、白色の放射光からneV幅の単色のガンマ線のみを実験に用いていることにも関係して、大部分の放射光を実験に用いていない。より多くの入射光を有効に用いてさらに効率よく実験を行うため、複数の異なるエネルギーの単色ガンマ線を用いて構築された時間領域干渉計が、マルチラインの時間領域干渉計である。
　このセットアップではガンマ線放射体1、2として鉄箔を用いる。鉄中には33 Tの内部磁場が存在し、⁵⁷Fe原子核の磁気モーメントと相互作用することにより、励起状態および基底状態の鉄原子核のエネルギー準位はそれぞれZeeman分裂を起こしている（図6(a)参照）。この分裂幅は数十neV程度で、電子系のZeeman分裂幅に比べて大変小さく、核エネルギー準位の超微細構造分裂と呼ばれる。

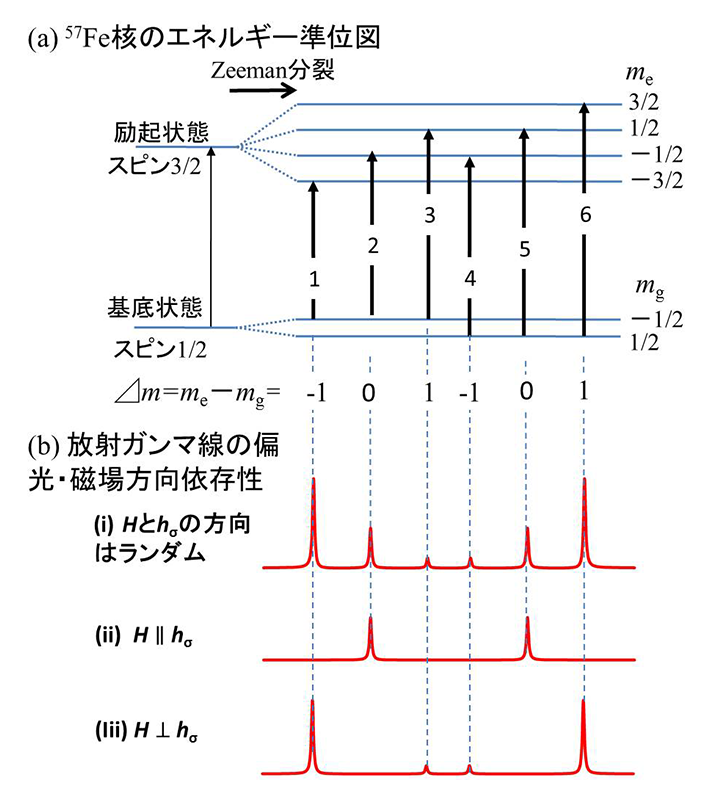
図6　(a) α-Fe中の核準位の分裂と、(b) 放射ガンマ線の偏光・内部磁場方向依存性

　⁵⁷Feの核準位間の遷移に関する選択則により、図6(a)に示されるような6種の遷移が許容となる。励起状態の磁気量子数m_eと基底状態の磁気量子数m_gの差Δmに関して、6種の遷移は、-1, 0, 1のいずれかの値をとる。各Δmを有する遷移の遷移確率は、内部磁場Hの方向と入射放射光の磁場偏光ベクトルh_δの向きの関係性にそれぞれ大きく依存する。例えば、線2色性や磁気円2色性実験では電子系の準位間遷移に関するこのような選択則を利用して物性研究を行っている。H⊥kとし（kは波数ベクトル）、さらに、H‖h_δならばΔm = 0の遷移のみが、H⊥h_δならばΔm = ±1の遷移のみが許容される。それらの条件でそれぞれ得られるガンマ線のエネルギースペクトルをそれぞれ図6(b)中に示す。
　マルチラインのガンマ線準弾性散乱法では、このような選択則を利用し、ガンマ線放射体1、2にそれぞれ、H‖h_δおよびH⊥h_δと磁場をかけることでエネルギー的に異なる複数のエネルギーのガンマ線が両者から放射されるような条件をつくる。このときの実験セットアップの概念図を図7に示す。図にはマルチライン法を反映するガンマ線のエネルギースペクトルが描かれている。1と番号付けられた放射体1起源のプローブガンマ線のピークでは、試料の拡散の影響を受けてエネルギー幅が広がる。一方、2と番号付けされた放射体2起源のリファレンスガンマ線のピークでのエネルギー幅は、試料による散乱の影響を受けない。時間領域上ではこれらの干渉の結果生じる複雑な量子ビートが測定される。その時間スペクトルの例を図7に示す。

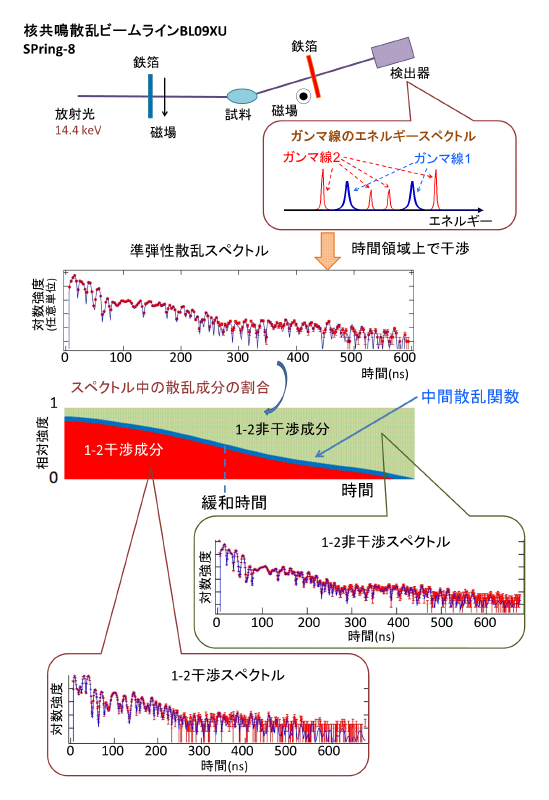
図7　マルチラインの時間領域干渉計法を用いた準弾性散乱実験により得られるガンマ線の時間スペクトル

　シングルラインの時間領域干渉計では、ガンマ線1と2の干渉項（量子ビート）はダイナミクスの影響（中間散乱関数）により時間的に消失していった。マルチライン法でもスペクトルの形状は複数の量子ビートが混在し複雑になるものの、基本的に同様のことが起こる。すなわち、中間散乱関数に従ってスペクトルの形状はプローブガンマ線1とリファレンスガンマ線2の成分間の干渉がある場合のスペクトル（1-2干渉スペクトル）から、プローブガンマ線1とリファレンスガンマ線2の成分間の干渉がない場合のスペクトル（1-2非干渉スペクトル）に変化する。ゆえに、両スペクトルをあらかじめ精度よく測定しておけば、準弾性散乱スペクトルにおけるそれらのスペクトルの成分比の時間変化を調べることにより、動的構造因子と等価な中間散乱関数を決定することができる。
　既存のシングルライン法では、量子ビートは時間とともに消失するのみであったが、マルチライン法では、1-2干渉スペクトルと1-2非干渉スペクトルはそれぞれ大きく異なった時間構造（ピーク位置）をもつため、両者間に大きな強度のコントラストがつき、ダイナミクスの影響を反映して量子ビートのパターンが劇的に変化する。このような高いコントラストに基づく高いダイナミクス測定効率も、マルチライン法を用いる利点である。

6. 応用例の紹介
　ガンマ線準弾性散乱法は過冷却液体、結晶、ガラス、および液晶などのソフトマターのダイナミクス研究に対して用いられている。過冷却液体のダイナミクス測定はガラス転移のメカニズムの理解に有用である^[11][11] M. Saito et al.: Phys. Rev. Lett. 109 (2012) 115705.。これまで過冷却液体、およびガラス状態のo-terphenyl^[11-13][11] M. Saito et al.: Phys. Rev. Lett. 109 (2012) 115705.
[12] M. Saito et al.: Hyperfine Interact. 226 (2014) 629-636.
[13] T. Kanaya et al.: J. Chem. Phys. 140 (2014) 144906.、polybutadiene^[13][13] T. Kanaya et al.: J. Chem. Phys. 140 (2014) 144906.、glycerol^[12,14][12] M. Saito et al.: Hyperfine Interact. 226 (2014) 629-636.
[14] M. Saito et al.: Hyperfine Interact. 237 (2016) 22.、ionic liquid 1-butyl-3-methylimidazolium iodide^[15,16][15] M. Saito et al.: J. Phys.: Conf. Ser. 217 (2010) 012147.
[16] M. Saito et al.: Appl. Phys. Express 2 (2009) 026502.の研究がなされている。また、ordered alloy中の拡散も報告されている^[17,18][17] B. Sepiol et al.: Hyperfine Interact. 126 (2000) 329-333.
[18] M. Kaisermayr et al.: Eur. Phys. J. B 20 (2001) 335-341.。液晶分子の拡散ダイナミクスもガンマ線を用いた準弾性散乱法で調べられており、典型的なサーモトロピック液晶4-n-octyl-4-cyanobiphenylと部分的にフッ素化された炭化水素鎖をもつ液晶が測定され、それらの非等方的な緩和時間からミクロな構造が議論されている^[19][19] M. Saito et al.: J. Phys. Soc. Jpn. 81 (2012) 023001.。
　これまでに得られた新しい結果の例として、典型的な過冷却液体o-terphenylの冷却過程におけるミクロなダイナミクスの研究を紹介する^[11][11] M. Saito et al.: Phys. Rev. Lett. 109 (2012) 115705.。この液体を冷却していくと、分子間スケールの緩和時間はガラス転移温度近傍に向けて発散的に遅くなる。図8(a)に実験で得られたミクロな緩和時間のq依存性のべき指数の温度依存性を示す。緩和時間のq依存性を測定することで、ミクロな拡散の局所的な度合いを調べることができ、べき指数が2から大きくなるほど拡散は局所的になっていると解釈できる。実験の結果、o-terphenylでは290 Kにおいて拡散が局所的になり始めることが分かった。これまでの他の測定でも290 Kで様々なダイナミクスの変化が観測されており、この温度で分子環境が徐々に局所的に液体的な振る舞いから固体的な振る舞いに変化し始めていると考えられている。我々の実験でも、290 Kにおいて分子環境が固体ライクとなり始める様子が拡散の局所化という観点から観測されたと考えている。一方、図8(b)に示される緩和時間の温度依存性に関しては、分子内スケールの緩和時間（q = 23 nm^-1）は、278 Kで発散的な温度依存性からより温度依存性が穏やかなArrhenius則に従うようになることが見出された。この変化は、冷却に伴い278 Kから本来固体中で見られる活性化過程であるJohari-Goldstein β過程が生じたことによると結論できた。すなわち、290 Kからさらに冷却すると、278 Kにおいて活性化過程が起こるのに十分な時間スケールまで分子環境が固体的となることが分かった。このように、過冷却液体中ではミクロなダイナミクスは冷却に伴い段階的に固体的な特徴を帯び始めることが明らかにされた。

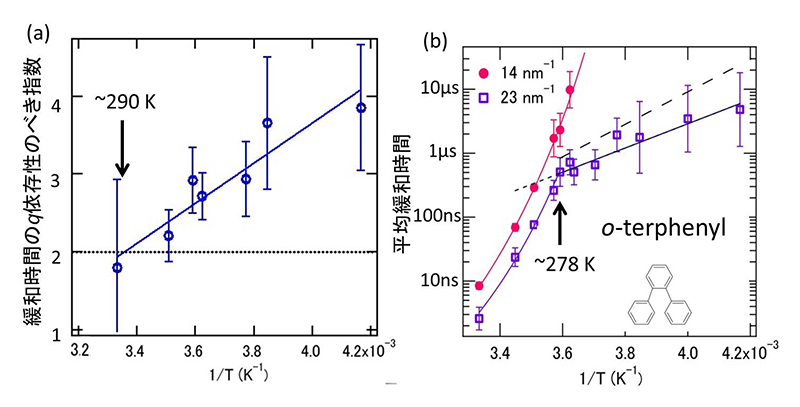
図8　o-terphenylの冷却過程におけるミクロなダイナミクスの結果、 (a) 緩和時間のq依存性のべき指数の温度変化、(b) 緩和時間の温度依存性

7. まとめと今後の展開
　図7中の準弾性散乱スペクトル例から分かるように、現在のところ時間領域干渉計を用いて600 ns程度まで時間スペクトルを観測することができ、凝縮系のns～µsダイナミクス測定が可能となっている。一方、中性子スピン・エコー法では、nmスケールの構造のダイナミクスに関しては典型的に数百nsまでの時間レンジで測定できる。ゆえに、nmスケールの100 ns程度のダイナミクス研究に関しては、両者を相補的に用いた研究を行うことができ、プローブの違いを有効に利用することで1手法により得られる結果よりも遥かに多くの情報を得ることができる。
　中性子スピン・エコー法にはダイナミクスを観測する空間スケールを小さくすると、緩和の観測時間スケールが相対的に短くなるという特性がある。このため、中性子を用いて、原子スケール（0.1 nmスケール）のµsの緩和ダイナミクスを観測するのは現実的ではない。一方、時間領域干渉計は原子スケールにおいても比較的容易にµsスケールという長い時間スケールのダイナミクスを測定できるという特徴がある。
　核Bragg分光器を用いて白色放射光から単色ガンマ線をほぼ完全に切り出し、そのガンマ線を用いて準弾性散乱測定をエネルギー領域上で行う方法も提案されている^[20,21][20] J. Z. Tischler et al.: J. Appl. Phys. 79 (1996) 3686.
[21] R. Masuda et al.: Jpn. J. Appl. Phys. 48 (2009) 120221.。この方法には必ずしもセベラルバンチモード運転が必要でないという利点がある。この手法では、生成されたガンマ線のエネルギー幅が自然幅より大きくなってしまうなどの手法上の特性のため、数十ns程度より短い時間スケールのダイナミクス測定に適していることが示唆されている。
　このように、時間領域干渉計を用いたガンマ線準弾性散乱法は凝縮系の物性研究法として非常にユニークな手法であり、いまださらなる開発の余地がある。そして今後の装置開発により、さらに様々な対象への応用が可能となると考えられる。その効率よい測定のため、1バンチに比較的高い電流が蓄積され、340 ns以上のバンチ間隔を有する加速器運転におけるセベラルバンチモード（D、Fモード）の利用が本質的に重要である。この手法が今後益々発展していくためには、このようなセベラルバンチ運転等による放射光パルスの時間間隔制御が不可欠であり、そのうえで、より高輝度の放射光の利用ができるようになることを期待したい。

参考文献
[1] 齋藤真器名：固体物理 47 (2012) 11.
[2] 瀬戸誠：日本結晶学会誌 43 (2001) 405-412.
[3] 瀬戸誠：固体物理 44 (2009) 27.
[4] 菊田惺志：X線散乱と放射光科学 基礎編（東京大学出版会、2011）
[5] 細川伸也：分光研究 57 (2008) 301-312.
[6] A. Q. R. Baron：固体物理 44 (2009) 11.
[7] A. Q. R. Baron et al.: Phys. Rev. Lett. 79 (1997) 2823.
[8] G. V. Smirnov, V. G. Kohn and W. Petry: Phys. Rev. B 63 (2001) 144303.
[9] G. V. Smirnov et al.: Phys. Rev. B 73 (2006) 184126.
[10] M. Saito et al.: Hyperfine Interact. 206 (2012) 87-90.
[11] M. Saito et al.: Phys. Rev. Lett. 109 (2012) 115705.
[12] M. Saito et al.: Hyperfine Interact. 226 (2014) 629-636.
[13] T. Kanaya et al.: J. Chem. Phys. 140 (2014) 144906.
[14] M. Saito et al.: Hyperfine Interact. 237 (2016) 22.
[15] M. Saito et al.: J. Phys.: Conf. Ser. 217 (2010) 012147.
[16] M. Saito et al.: Appl. Phys. Express 2 (2009) 026502.
[17] B. Sepiol et al.: Hyperfine Interact. 126 (2000) 329-333.
[18] M. Kaisermayr et al.: Eur. Phys. J. B 20 (2001) 335-341.
[19] M. Saito et al.: J. Phys. Soc. Jpn. 81 (2012) 023001.
[20] J. Z. Tischler et al.: J. Appl. Phys. 79 (1996) 3686.
[21] R. Masuda et al.: Jpn. J. Appl. Phys. 48 (2009) 120221.

齋藤　真器名　SAITO Makina
京都大学原子炉実験所
〒490-0494　大阪府泉南郡熊取町朝代西二丁目
TEL : 072-451-2680
e-mail : msaito@rri.kyoto-u.ac.jp