Volume 22, No.1 Pages 8 - 13

1. 背景
　金属材料の分野では、機械特性の定性的な理解から定量予測へと大きくシフトしようとしている。例えば降伏強度や成形性を定量予測しようという試みがなされており、実現すればモノづくりの高度化に貢献することは言うまでもない。自動車工業においては金属材料の塑性加工が多用されているが、高ひずみ領域における塑性加工CAE（Computer Aided Engineering）の予測精度が不十分なため試作が避けられない。自動車工業においてコスト削減は最重要課題の1つであり、試作はCAEの精度向上により克服すべきコストである。しかし、鉄鋼材料を始めとする実際の金属材料の塑性変形の数理モデリングは容易ではない。アプローチのひとつは、製造現場でもよく知られている有限要素法を使った工学的手法である。この手法では、応力とひずみの関係を定式化した構成方程式を設定し、有限要素法により数値解析を行う。例えば多結晶組織のような材料の不均一性は要素を小さくすることで表現する。結晶粒を有限要素分割できれば、結晶塑性論に基づく多結晶塑性モデリングが可能であり、最近では、結晶塑性論に転位論の考え方を取り込んだマルチスケールモデリングも登場している。しかし、現実の部品の大きさから結晶粒までを有限要素分割するには(10⁵)³オーダーの要素数を要するため現状では難しい。一方、究極的な数理モデルとして、原子間ポテンシャルを設定し、原子1個1個の運動を数値解析する原子シミュレーションも検討されている。分子動力学法では、転位のすべり運動や、転位の増殖、転位同士の相互作用、固溶原子・分散粒子・析出物と転位の相互作用、粒界における転位の堆積・応力集中といった塑性変形の素過程とも言える現象がシミュレーション可能である。しかし、1つの結晶における周期境界条件では従来と同じく現象の定性的な理解にとどまってしまうため、粒界ネットワークを記述できるスケールに拡張する必要があるが、それには(10⁵)³オーダーの原子数を要するため現状ではやはり難しい。
　数理モデルによる定量予測はまだ始まったばかりであり、計算科学の発達に伴ってそれぞれの手法がスケールを拡張し結晶粒スケールに到達することは、いずれ可能となろう。そうすれば結晶粒スケールを架け橋として原子シミュレーションに基づいた部品スケールのCAEの可能性が見えてくる。ここで重要な問題は、それぞれ結晶粒スケールに拡張したモデルのシミュレーションが実際の材料の挙動と一致しているかどうか確かめる実験手法が確立されていない点である。このような実験手法には、(1) 結晶粒スケールの顕微鏡法、(2) 応力及びひずみの定量評価、(3) 結晶方位の決定、(4) バルク内部3次元観察、(5) 非破壊観察といった機能が要求される。H. F. Poulsenらによって提案された、Three-dimensional x-ray diffraction microscopy（3DXRD）^[1][1] H. F. Poulsen: J. Appl. Cryst. 45 (2012) 1084-1097.は、上のような要件を満たすことのできる放射光を使った新しい実験手法として有力視されている。
　3DXRD法は言わば多結晶の回転結晶法である。多結晶試料に単色X線を入射し、試料を回転させながら、試料透過方向に配置した2次元検出器により複数の結晶粒からのX線回折斑点を記録する。検出器は試料近く（10 mm以内）に配置する高空間分解能検出器D1と、遠く（100 mm以上）に配置する大面積検出器D2を用いる。D2の回折画像の中から、結晶構造及び格子パラメータを既知として“多結晶指数付け”^[2-7][2] E. M. Lauridsen et al.: J. Appl. Cryst. 34 (2001) 744-750.
[3] W. Ludwig et al.: Rev. Sci. Instrum. 80 (2009) 033905.
[4] M. Moscicki et al.: Mater. Sci. Eng. A 524 (2009) 64-68.
[5] J. Oddershede et al.: J. Appl. Cryst. 43 (2010) 539-549.
[6] J. V. Bernier et al.: J. Strain Anal. Eng. Des. 46 (2011) 527-547.
[7] J. K. Edmiston et al.: J. Appl. Cryst. 44 (2011) 299-312.により、ある結晶粒からの回折斑点を抽出する。回折斑点の位置からその結晶粒の平均の結晶方位を決定し、格子パラメータを変数として結晶粒の平均の格子パラメータを決定する。何らかの方法で定義した無ひずみ時の格子パラメータとの差をとることで弾性ひずみを求めることができる。全ての格子パラメータが得られるため、弾性ひずみテンソルを求めることができる。したがって、応力テンソルに変換することも可能である^[5][5] J. Oddershede et al.: J. Appl. Cryst. 43 (2010) 539-549.。これをX線が入射した各結晶粒に適用することにより、各結晶粒の粒内平均の結晶方位と応力が得られる。結晶粒の位置と形状の解析には、シート状の入射ビームとD1を用いる。D1における各回折斑点の位置と形状から、シート状ビーム入射断面内における結晶粒の位置と形状が解析される。回折斑点の形状及び強度分布も詳細に解析することにより、結晶粒内の結晶方位分布を再構成することが可能である^[8,9][8] S. F. Li et al.: J. Appl. Cryst. 45 (2012) 1098-1108.
[9] R. Pokharel et al.: Int. J. Plasticity 67 (2015) 217-234.。これにより、塑性ひずみに相当する物理量が得られる。ただし、結晶粒内の応力分布の解析はまだ達成されていない。50 keV以上の高エネルギーX線を使用するため、ビーム入射断層面内において、1 × 1 mm²程度の試料外寸をもつ鉄系試料の観察が可能であり、微小引張試験片の塑性変形その場観察が実現されている。この断層の積み重ねにより3次元再構成が行われる^[9,10][9] R. Pokharel et al.: Int. J. Plasticity 67 (2015) 217-234.
[10] G. Winther et al.: Int. J. Plasticity 88 (2017) 108-125.。これにより原理的には上述の(1)及び(3)−(5)を可能にしている。(2)に関しては塑性ひずみについては粒内分布、応力については粒内平均（第2種応力と呼ばれる）が得られる。
　3DXRD法では回折斑点の位置を基に解析を行うため、異なる結晶粒からの回折斑点がオーバーラップしないような実験条件を満たさなければならない。そのため、熱処理により結晶粒径を粗大粒（100 µm程度）化した試料を使って断層面内の結晶粒数を減らした実験がよく報告されている。実際の鉄鋼材料によく見られる粒径（10 µm程度）では、1 × 1 mm²微小引張試験片断層面内における結晶粒数が多すぎるため、回折斑点がオーバーラップし解析不能となる。筆者らはこの点が3DXRD法の最大の問題であると考えている。なぜなら、実験手法の制約により実際の材料とは大きく異なる試料をモデリングすることは、実用金属材料の塑性加工CAE高精度化を目指す筆者らにとっては本末転倒だからである。この問題を克服するために、筆者らは細い入射ビームを使って一度にX線が入射する結晶粒数を減らすことによって、回折斑点のオーバーラップを抑える方法を提案した^[11][11] Y. Hayashi et al.: J. Appl Cryst. 48 (2015) 1094-1101.。細いビームを使った走査型の顕微鏡法であることから走査型3DXRD法（Scanning 3DXRD）と呼んでいる。走査型3DXRD法では、試料を走査することにより空間分解を行うためD1を必要としない。そのため試料周りの空間が広くとれるため、その場観察引張試験が容易になるという利点もある。また、3DXRD法では粒内方位分布（及び粒内応力分布）を解析するためにはD1上の回折斑点の強度分布データも必要となるが、一般にX線2次元検出器の空間分解能とダイナミックレンジはトレードオフの関係にあるため、粒内分布の再構成は容易ではない。一方、走査型3DXRD法では、粒内分布の解析においてもD2上の回折斑点の位置情報のみを用いて強度情報は用いないため検出器のダイナミックレンジは不要である。
　本稿では、まず走査型3DXRD法の方法論を概説する（2節）。本手法では走査型の利点を最大限に活用するため、3DXRD法とは異なる再構成法を新たに構築した。これは経験則に基づく工学的アプローチであるため、シミュレーションにより本再構成法の妥当性及びその限界を調べた（3節）。検証実験については2例紹介する（4−5節）。

2. 方法
　走査型3DXRD法では細いビームを多結晶試料に入射し、Fig.1に示すような回転ωにより試料を回転しながら、D2により回折画像を連続的に記録する。ωを180°回転したらX方向にΔXだけ並進させる。これを繰り返し、ω及びXで2次元スキャンした回折画像データを得る。2次元スキャンデータから入射ビームが任意の点Q(x,y)を常に通るような(ω,X)の関係を満たす回折画像データを抽出する。この条件を満たすとき、簡単のためx方向の入射ビーム幅をΔXとすると、180°回転の間、点Qを中心とした直径2ΔXの領域に入射ビームが概ね集中する。そこで、抽出した回折画像の中には、点Q及びその周り直径2ΔXの空間を占める結晶粒の回折斑点が最も多く記録されていると仮定する。正確には、ある結晶粒から検出される回折斑点数Nは結晶方位に依存するため、Nの理論的な最大値をMとして、N/Mが最大となる結晶粒が点Qを占める結晶粒であると仮定する。Nは3DXRD法により構築された“多結晶指数付け”により決定することができ、Mは理論的に求められる。多結晶指数付けにより同時にその結晶粒の結晶方位も求まる。したがって、点Q及びその周り直径2ΔXの空間を占める結晶粒及びその結晶方位が求まる。直径2ΔXは位置不確定性をもたらすため、空間分解能は2ΔX程度であると予想される。また、位置不確定性の観点からΔXは入射ビーム幅もしくはX方向スキャンステップのどちらか大きい方と定義できる。点Qを視野全体にわたって掃引することにより2次元結晶方位マップが得られる。この2次元マップをz方向に積み重ねることにより3次元結晶方位マップが得られる。

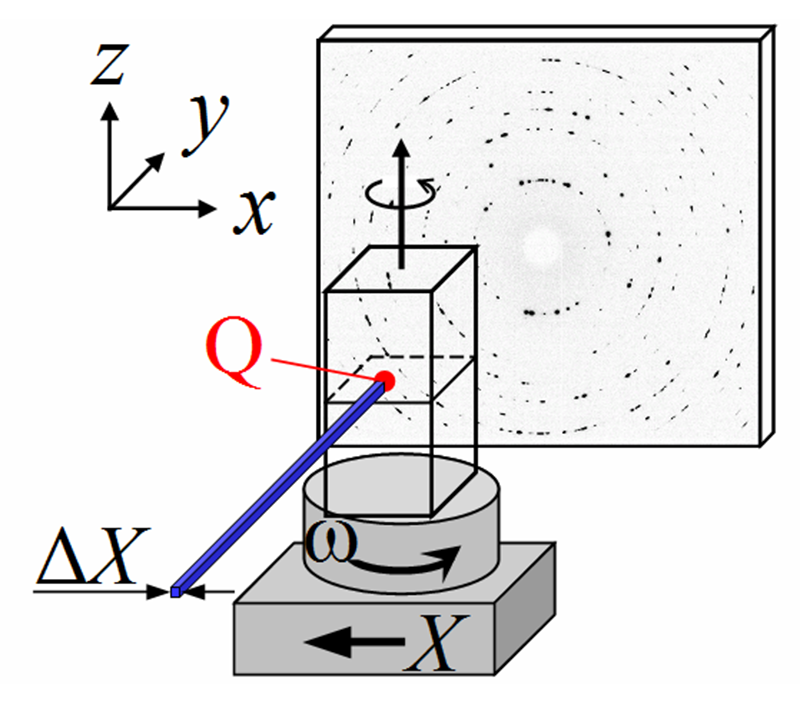
Fig.1　走査型3DXRD顕微鏡法のセットアップ。

3. 再構成シミュレーション
　走査型3DXRD法における再構成方法の妥当性を検証するために、最初のステップとして、再構成シミュレーションにより結晶粒形状の再現性を調べた。用いた結晶粒形状評価用ファントムをFig.2(a)に示す（再構成法評価用人工モデルをファントムと呼ぶ）。結晶粒分布ファントムでは各結晶粒を要素分割し、結晶粒内部では均一な結晶方位をもたせている。Fig.2(a)において色は結晶方位を、実線は結晶粒界を示している。入射ビーム幅（及びX方向スキャンステップ）ΔXを結晶粒径よりも十分小さくとり、(ω,X)の関数として各結晶粒の回折斑点位置を計算した。次にファントムの情報は使わずに、計算した回折斑点位置データから前節で述べた方法により結晶粒マップを再構成した。シミュレーション方法の詳細は文献[11]を参照されたい。再構成された結晶粒マップをFig.2(b)に示す。Fig.2(b)において色は再構成された結晶粒分布、実線はファントムの結晶粒界を示している。Fig.2(b)より、(i) 小さい粒に隣接している大きい粒はさらに大きくなる、(ii) 大きい粒に隣接している小さい粒はさらに小さくなるか消失する、(iii) 結晶粒の凹凸形状が丸みを帯びる、といったアーティファクトが生じることが分かる。結晶粒形状ずれ量を定量的に調べるために、再構成マップの結晶粒界とファントムの結晶粒界の位置ずれ量W_bを評価した。その結果をヒストグラムとしてFig.2(c)に示す。ヒストグラムの横軸W_bはΔXにより規格化している。ヒストグラムよりW_bは概ね2ΔX以下に集中していることが分かる。したがって、本シミュレーションでは結晶粒形状の再現性は、～2ΔX程度であると言える。これは前節で予想した空間分解能と一致する。

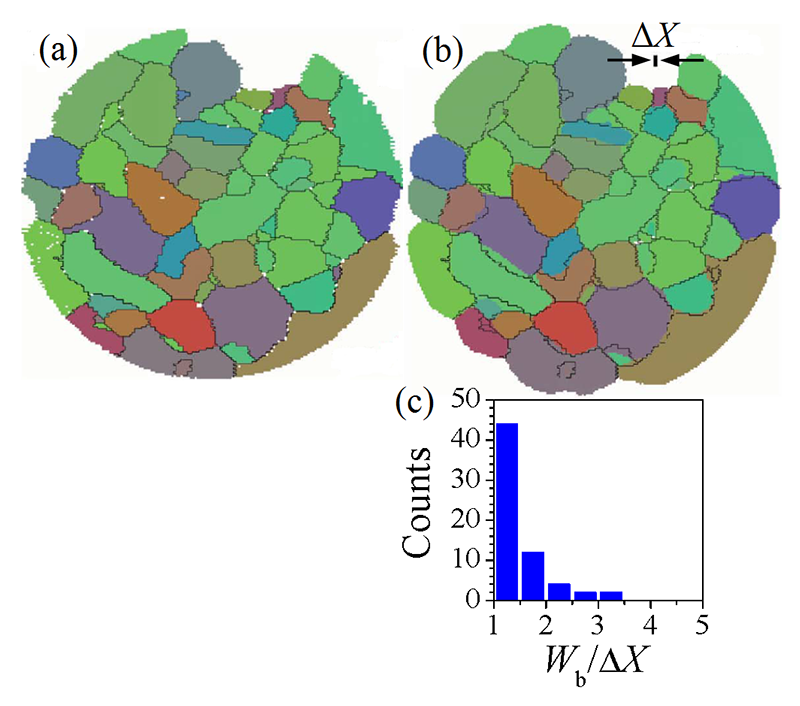
Fig.2　再構成シミュレーションに用いた、(a) 結晶粒形状評価用結晶粒分布ファントムと、(b) シミュレーションにより得られた結晶粒マップ。(a)及び(b)中の両方にファントムの結晶粒界を実線で示している。(c) 入射ビーム幅ΔXで規格化したW_bのヒストグラム。W_bはファントムの結晶粒界位置とシミュレーションにより得られた粒界位置のずれ量である。

4. 粗大粒試料による検証実験
　走査型3DXRD法の初めての実験を粗大粒化純鉄試料と20 µmビームを用いて行った。供試材として直径0.5 mmの純Fe線（純度99.5％）を用意し、1250℃・5時間の粗大粒化熱処理を施した試料を用いた。BL33XU豊田ビームラインにおいて、アンジュレータ放射光をSi220チャネルカット分光器により40 keVに単色化し、20 × 20 µm²のスリットを通して試料に入射した。D2にはフラットパネル検出器を用いた。ΔXを25 µm、z方向のスキャンステップを25 µmとし、走査型3DXRD法により3次元結晶方位マッピングを行った。次に試料を切り出し、電子線後方散乱回折（EBSD）法により切り出し表面の結晶方位マッピングを行った。結晶粒の相対方位及び相対位置を頼りに、EBSD方位マップ中で観察された結晶粒を走査型3DXRDによる3次元方位マップの中から探し出した。3次元マップ中、一致した結晶粒が最も多く含まれるxy面2次元マップをEBSD観察と一致した走査型3DXRDレイヤとした。一致した走査型3DXRDレイヤにおける2次元結晶方位マップをxy面内におけるボクセルサイズΔxを12.5 µmとしてもう一度再構成した（xy面内ボクセルサイズΔxは入射ビーム幅及びX方向スキャンステップΔXと必ずしも一致しなくてよいが、原理的な空間分解能はΔxには依存せずΔXに依存する。詳しくは文献[11]を参照されたい）。これを走査型3DXRDで再構成された方位マップとして、走査型3DXRD及びEBSDで評価された結晶粒径を比較した。
　走査型3DXRD及びEBSDにより得られた方位マップをそれぞれFig.3(a)及び3(b)に示す。両マップで一致した結晶粒の直径の比d_3DXRD/d_EBSDを、d_EBSD/ΔXに対してプロットした結果をFig.3(c)に示す。ここで、ΔX ＝ 25 µmである。Fig.3(c)のグラフ中には走査型3DXRD再構成シミュレーションにより推定された空間分解能2ΔXによる粒径比の上限と下限を実線で示している。また、走査型3DXRD方位マップのxy面内におけるボクセルサイズΔxによる粒径比の下限を点線で示している。粒径比がこれら上限・下限以内に収まっていることが分かる。これは、走査型3DXRD法の空間分解能を2ΔXと仮定すると、走査型3DXRD及びEBSDによる粒径評価値が一致していることを表している。

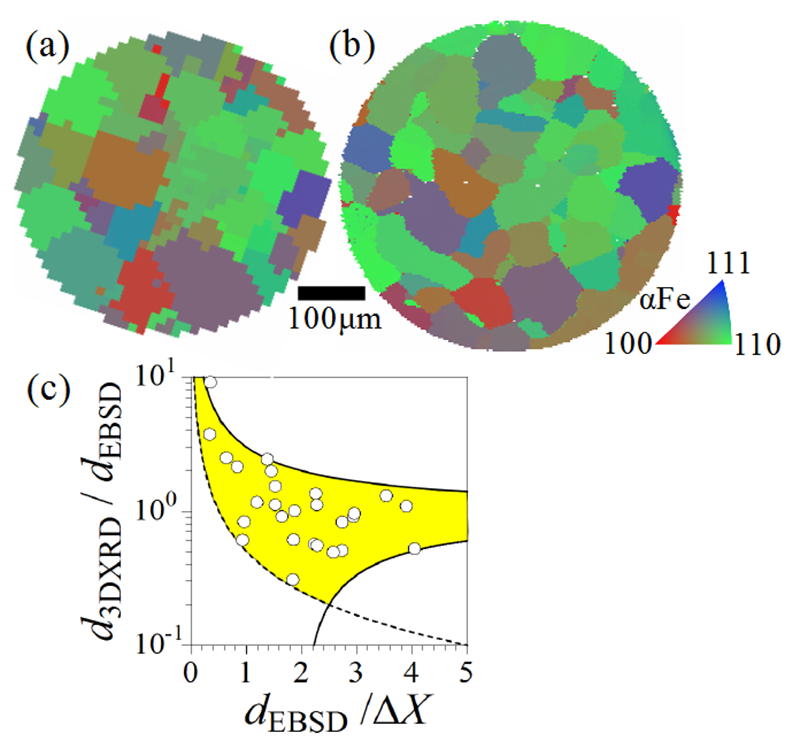
Fig.3　(a) 走査型3DXRD法及び、(b) EBSD法により得られた粗大粒化純Fe線材の結晶方位マップ。結晶方位はz方向の逆極点図表示。(c) 両マップで一致した結晶粒の粒径比の粒径（直径d）依存性。(c)グラフ中の実線は走査型3DXRD法の空間分解能を2ΔXと仮定したときの粒径比の上限及び下限(d-2ΔX)/dを示す（＋は上限、－は下限）。点線は走査型3DXRD法のxy面内におけるボクセルサイズΔxによる粒径比の下限Δx/dを示す。

5. マイクロビームを用いた実用鉄鋼材料の観察
　次に、マイクロビームを使った走査型3DXRD法により実際の鉄鋼材料を熱処理せずに2次元結晶方位マッピングを行った。供試材には一般塑性加工用として非常に広く実用に供されている冷間圧延鋼板SPCC（JIS G 3141）商用流通受け入れ材を用いた。EBSDにより評価したSPCC材（1 mm厚）の方位マップと粒径のヒストグラムをそれぞれFig.4(a)及び4(b)に示す。実験は、BL33XU豊田ビームラインにおいて50 keVマイクロビーム光学系を構築して行った^[12][12] Y. Hayashi et al.: AIP Conf. Proc. 1741 (2016) 050024.。アンジュレータ放射光をSi311二結晶分光器により50 keVに単色化し、Kirkpatrick-Baez配置400 mm長PtコートSiミラーにより集光した。集光サイズは半値全幅で幅1.3 × 高さ1.6 µm²、フラックスは、5.9 × 10⁹ photons/sであった。EBSD評価とは別ロットのSPCC材（1 mm厚）からワイヤカット加工により幅1 mmの試料を切り出し、試料長手方向をz方向とした。したがって、xy面内の試料断面積は1 × 1 mm²である。X方向スキャンステップを1 µmとしてxy面内の2次元結晶方位マッピングを行った結果をFig.4(c)に示す。3DXRD的手法により粒径20 µm・断面積1 × 1 mm²の金属試料において粒径が評価できる程度の結晶方位マップが得られたのはこれが初めてである。この結晶方位マップから得られた粒径のヒストグラムをFig.4(d)に示す。視野が狭いため統計ばらつきが見られるものの、平均値はおよそ15 µm、分布はおよそ5～25 µmとなっており、EBSDによる評価と概ね一致が得られている。結晶粒形状に着目すると、Fig.4(c)ではFig.4(a)のような滑らかな結晶粒界が再現されておらず、粒界位置が不鮮明である。実験装置の精度向上及び再構成アルゴリズムの精密化等により粒界位置の鮮明化は可能であると考えている。

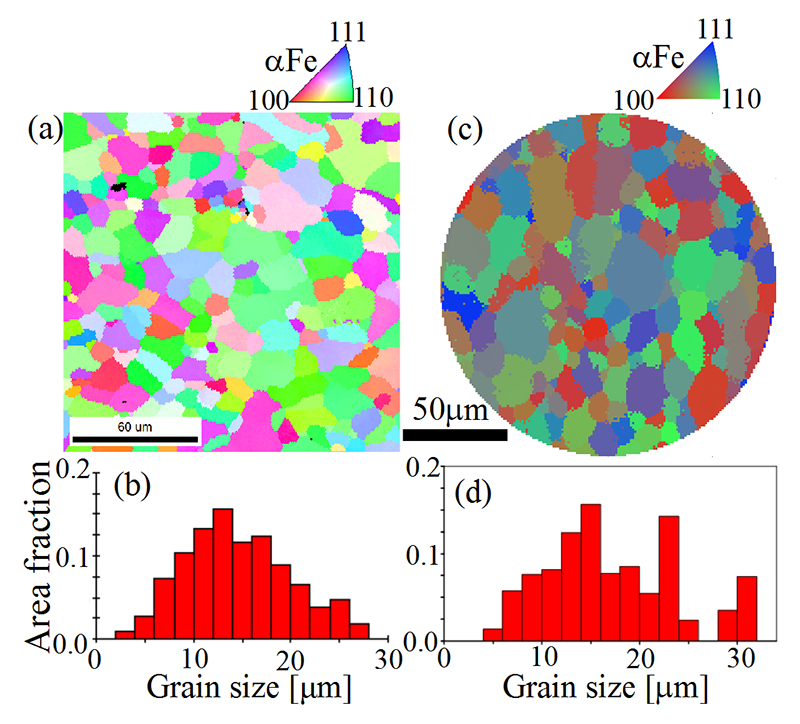
Fig.4　冷間圧延鋼板SPCC材のEBSD法による、(a) 結晶方位マップと、(b) 粒径（直径）ヒストグラム、及び、マイクロビームを用いた走査型3DXRD法による(c) 結晶方位マップと、(d) 粒径（直径）ヒストグラム。

6. まとめ
　3DXRD法は高エネルギー放射光X線を使って多結晶金属材料内部における結晶方位と応力の非破壊3次元観察を可能にした新しい手法である。筆者らは、3DXRD法を実際の材料に応用する際に最大の問題となる回折斑点のオーバーラップを解決するため、マイクロビームを用いて試料を走査する走査型3DXRD法を考案し、最初のステップとして結晶粒マッピングのシミュレーションと実験を行った。再構成シミュレーションでは、結晶粒形状の再現性の空間分解能は入射ビーム幅（またはスキャンステップ幅の大きい方）の2倍程度であることを推定した。実験では、粗大粒化純Fe線試料を用いて走査型3DXRDとEBSDにより同じ断面の結晶方位マッピングを行い、粒径を比較した結果、再構成シミュレーションにより推定された空間分解能と矛盾しないことを確かめた。実用へ向けて50 keVマイクロビームを使った走査型3DXRD装置を構築し、冷間圧延鋼板1 mm厚商用流通受け入れ材の非破壊結晶方位マッピングに初めて成功した。

7. 今後の展望
　これまでに一般塑性加工用鉄鋼材料の代表である冷間圧延鋼板SPCC材（平均粒径約20 µm）の非破壊結晶方位マッピングを達成した。その際、(1) 結晶粒スケールの顕微鏡法、(3) 結晶方位の決定、(5) 非破壊観察を達成した。今後は、一般鍛造用鉄鋼材料の代表であるフェライト・パーライト炭素鋼や自動車用高強度鋼板であるフェライト・マルテンサイト二相鋼への適用拡大を目指す。このため、フェライトとパーライトまたはフェライトとマルテンサイトの識別方法の検討を行う。また、(2) 応力及びひずみの定量評価、及び(4) バルク内部3次元観察への拡張を目指す。(4)への拡張は、走査型の欠点である長時間測定による位置ドリフトを克服するために試料及びビームの長時間位置安定化を図る。(2)については、走査型3DXRD法における結晶粒内方位及び応力分布の解析方法の構築を要する。本稿で紹介した結晶方位マッピング方法においても既に結晶粒内の方位分布をある程度反映した情報が得られているが^[13][13] Y. Hayashi et al.: Mater. Sci. Forum 777 (2014) 118-123.、ある結晶粒からの回折斑点は入射ビーム奥行き方向の平均になるため粒内方位差量及び応力の定量性が損なわれている。そこで、本再構成法によって得られる方位・応力マップを初期マップとし、実験データに基づいてマップを修正し粒内方位差量及び応力値を回復する再構成法を新たに構築する。合わせて、3DXRD法でまだ解決されていない難題である応力の粒内分布（第3種応力と呼ばれる）の再構成に取り組む。

謝辞
　高エネルギーマイクロビーム集光装置の導入にあたり、（公財）高輝度光科学研究センター（JASRI）の大橋治彦博士及び湯本博勝博士に多大なるご協力を頂きました。ここに感謝申し上げます。本研究開発はSPring-8 BL33XUにおいて実施したものです（課題番号2010A7002、2010B7002、2011B7002、2012A7002、2012B7002、2014B7002、2015A7002、2015B7002、2016A7002）。また、本研究はJSPS科研費JP22760571、JP26870932の助成を受けたものです。実験及び解析にあたり（株）豊田中央研究所の瀬戸山大吾氏、門浦弘明氏、高谷恭弘氏、鈴木智博氏にご協力頂きました。

参考文献
[1] H. F. Poulsen: J. Appl. Cryst. 45 (2012) 1084-1097.
[2] E. M. Lauridsen et al.: J. Appl. Cryst. 34 (2001) 744-750.
[3] W. Ludwig et al.: Rev. Sci. Instrum. 80 (2009) 033905.
[4] M. Moscicki et al.: Mater. Sci. Eng. A 524 (2009) 64-68.
[5] J. Oddershede et al.: J. Appl. Cryst. 43 (2010) 539-549.
[6] J. V. Bernier et al.: J. Strain Anal. Eng. Des. 46 (2011) 527-547.
[7] J. K. Edmiston et al.: J. Appl. Cryst. 44 (2011) 299-312.
[8] S. F. Li et al.: J. Appl. Cryst. 45 (2012) 1098-1108.
[9] R. Pokharel et al.: Int. J. Plasticity 67 (2015) 217-234.
[10] G. Winther et al.: Int. J. Plasticity 88 (2017) 108-125.
[11] Y. Hayashi et al.: J. Appl Cryst. 48 (2015) 1094-1101.
[12] Y. Hayashi et al.: AIP Conf. Proc. 1741 (2016) 050024.
[13] Y. Hayashi et al.: Mater. Sci. Forum 777 (2014) 118-123.

林　雄二郎　HAYASHI Yujiro
（株）豊田中央研究所　分析部
〒480-1192　愛知県長久手市横道41番地の1
TEL : 0561-63-4300
e-mail : y-hayashi@mosk.tytlabs.co.jp

広瀬　美治　HIROSE Yoshiharu
（株）豊田中央研究所　分析部
〒480-1192　愛知県長久手市横道41番地の1
TEL : 0561-63-4300
e-mail : e0432@mosk.tytlabs.co.jp

妹尾　与志木　SENO Yoshiki
（株）豊田中央研究所　分析部
〒480-1192　愛知県長久手市横道41番地の1
TEL : 0561-63-4300
e-mail : y-seno@mosk.tytlabs.co.jp

吉田　友幸　YOSHIDA Tomoyuki
（株）豊田中央研究所　分析部
〒480-1192　愛知県長久手市横道41番地の1
TEL : 0561-63-4300
e-mail : tom-yoshida@mosk.tytlabs.co.jp