Volume 22, No.1 Pages 17 - 21

1. はじめに
　『百聞不如一見』は、「何事も自分の目で直接見た方がよくわかる」という意味の中国の故事であるとともに、顕微鏡開発者が好きな言葉の一つである。確かにいろいろな状況証拠を見せるより、一つの画像を見せた方が説得力が増す場合が多い。今日において、可視光顕微鏡や電子顕微鏡によって美しいマイクロ・ナノスケール画像を簡単に見ることができるようになった。しかし、これらとて見えないもの・現象はあるはずである。さらに説得力のある画像を撮るために、今でも世界中で様々な顕微鏡が開発され続けている。
　X線顕微鏡もまたその発展中の顕微鏡の一つである。これを使えば他の顕微鏡では見られない面白いものを見ることができる。短い波長であるため高い分解能が期待でき、X線の持つ高い透過能を生かして物質内部を見ることもでき、高いエネルギーを生かして分析（蛍光X線分析、XAFS分析など）しながら見ることもできる。そのため、様々なX線顕微鏡（結像型、走査型、レンズレスイメージング型 ･･･）が開発されている。本解説は、結像型にフォーカスを当て、筆者が開発中の新しい顕微鏡について解説する。
　先人の努力（フレネルゾーンプレートの開発^[1,2][1] T.-Y. Chen, Y.-T. Chen, C.-L. Wang, I. M. Kempson, W.-K. Lee et al.: Opt. Express 19 (2011) 19919-19924.
[2] Y. Suzuki, A. Takeuchi, H. Takenaka and I. Okada: X-Ray Opt. Instrum. 2010 (2010) 1.、X線屈折レンズの開発^[3][3] C. G. Schroer, O. Kurapova, J. Patommel, P. Boye, J. Feldkamp et al.: Appl. Phys. Lett. 87 (2005) 124103.）によってX線を結像することはそれほど難しくはなくなった。一方で未だ解決できない問題も存在する。それは色収差なく結像することである。色収差は波長によって焦点距離が変わる現象として理解できる。今のところ、放射光実験では高分解能な分光器を用いているため、あまり色収差が議論されることはないが、今後登場する様々なアプリケーション（顕微分光など）を考えると、色収差なく結像できる結像システムが望まれている。
　色収差をなくす方法の一つとして、X線全反射現象に基づいた反射レンズが知られている。X線全反射現象は、波長依存性が非常に低いため、実用的には色収差はほぼないと考えてよい。また、全反射現象は高い反射率を持つため、高い結像効率（レンズに入射する光の内、結像に寄与する光の割合）を実現できる。一方で、デメリットは、ミラー作製が難しい点と、複数曲面を組み合わせなければならない関係でそのアライメントが難しい点である。
　本研究の目的は、様々な困難を有する結像ミラーを使って高分解能かつ色収差のない顕微鏡を開発することであり、これによって結像ミラーに関する様々な技術を確立することである。

2. Advanced Kirkpatrick-Baezミラー光学系
　本研究では、結像ミラーとして、Advanced Kirkpatrick-Baez（KB）ミラー^[4][4] R. Kodama, N. Ikeda, Y. Kato, Y. Katori, T. Iwai et al.: Opt. Lett. 21 (1996) 1321-1323.（図1(b)）を採用した。本光学系は、一次元的には、Wolterミラー^[5][5] H. Wolter: Ann. Phys. 445 (1952) 94-114.（図1(c)）と同等であって、これらがKBミラー^[6][6] P. Kirkpatrick and A. V. Baez: J. Opt. Soc. Am. 38 (1948) 766-774.（図1(a)）のようにタンデムに直交配置されている。通常、集光光学系として用いられるKBミラー光学系では、コマ収差（光軸からずれて入射した光がぼける現象）が強く、広い視野を得られない。一方で、Advanced KBミラーやWolterミラーでは、2枚の反射面（楕円と双曲）を経由することでコマ収差がほとんど補正されている（KBミラーに2枚のミラー加えることでコマ収差を補正しているため、“Advanced” KBミラーと呼ばれている）。あえて、WolterミラーではなくAdvanced KBミラーを採用した理由は、ミラー作製難易度を下げるためである。Wolterミラーのような立体的なミラーでは、サジタル方向（光軸と直交する方向）に非常に大きな曲率を持ち、さらにそれが円筒の内面にあるため、加工と形状計測が非常に難しい。これを回避するために、Advanced KBミラーでは、縦横方向を別々のミラーペアーで結像する（KBミラーと同じコンセプト）。これによって、ミラー形状はほとんど平坦な一次元的な形状を有するミラーとなり、これは現在の技術でも作製可能である。

図1　様々なX線ミラー。(a) Kirkpatrick-Baezミラー、(b) Advanced Kirkpatrick-Baezミラー、(c) Wolterミラー。

　ただし、そうは言ってもその実現難易度は非常に高い。初めに知らなければならないことは、どの程度の作製精度とアライメント精度が必要であるのかである。目指す分解能は回折限界近傍であるため、フレネルキルヒホッフ回折積分に基づいた波動光学シミュレータを開発し、その見積もりを行った^[7,8][7] S. Matsuyama, M. Fujii and K. Yamauchi: Nucl. Instr. Meth. Phys. Res. 616 (2010) 241-245.
[8] S. Matsuyama, N. Kidani, H. Mimura, Y. Sano, Y. Kohmura et al.: Opt. Express 20 (2012) 10310-10319.。本シミュレータは、ミラー上に形状誤差を与えたり、ミラー配置にずれを与えたりでき、その状況を考慮した上で反射ごとにステップバイステップで波動伝搬を計算できる。これによって、どの程度の誤差まで許されるのかを正確に計算した。許容アライメント誤差解析の一例として、理想的な場合と、2つのミラーを同時に傾けた場合（つまりoff-axis条件）について計算した結果を示す（図2）。理想ミラー配置でも点広がり関数がボケている理由は、回折の影響であり、これが回折限界に相当する。様々な計算結果より、表1に示すようなアライメント精度が必要であることがわかった。これらを同時に達成することは非常に難しいが、工学的には不可能な値ではない。また、同様に許容形状誤差についても解析した。この結果は、簡易的な見積もりが可能なブラッグの式^[9][9] H. Mimura, S. Handa, T. Kimura, H. Yumoto, D. Yamakawa et al.: Nat. Phys. 6 (2010) 122-125.から得た結果とよく一致し、おおよそ3 nmとなった。さらに言うなら、縦横方向はそれぞれ2回の反射を経るため、このような形状誤差が波面誤差として蓄積される。有効視野全体で分解能に乱れがないためには、各反射で1.5 nm（λ/8に相当）以下の許容誤差に抑えることが求められる。この点はKBミラーよりも厳しい条件であり、KBミラーのおよそ半分の形状誤差しか許容できないことになる。

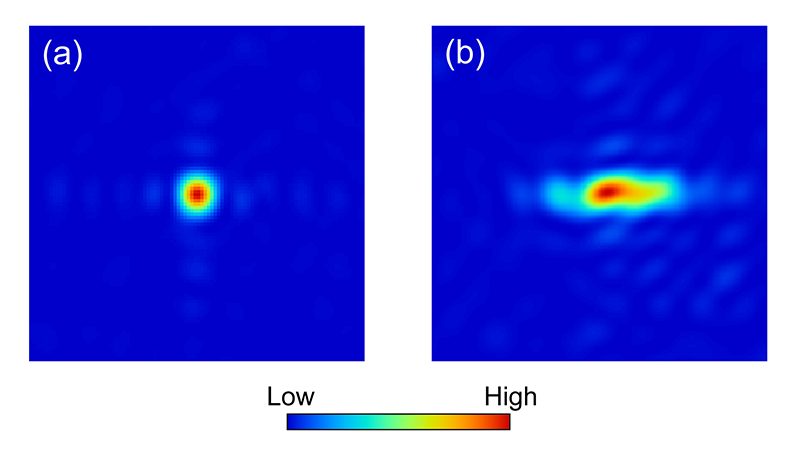
図2　波動光学シミュレータによって計算した点広がり関数。(a) 理想的な状態、(b) ミラー全体を80 µrad傾けた状態。X線エネルギー：10 keV。

表1　許容アライメント精度

アライメント軸		許容誤差
		縦結像	横結像
入射角 （µrad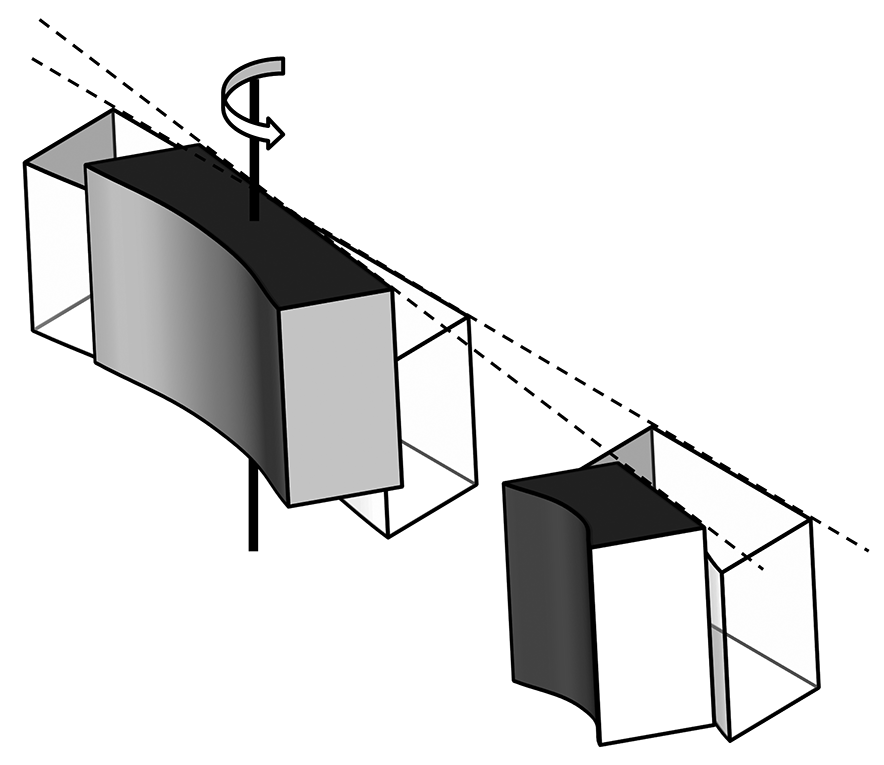）		+/-88	+/-57
相対角 （µrad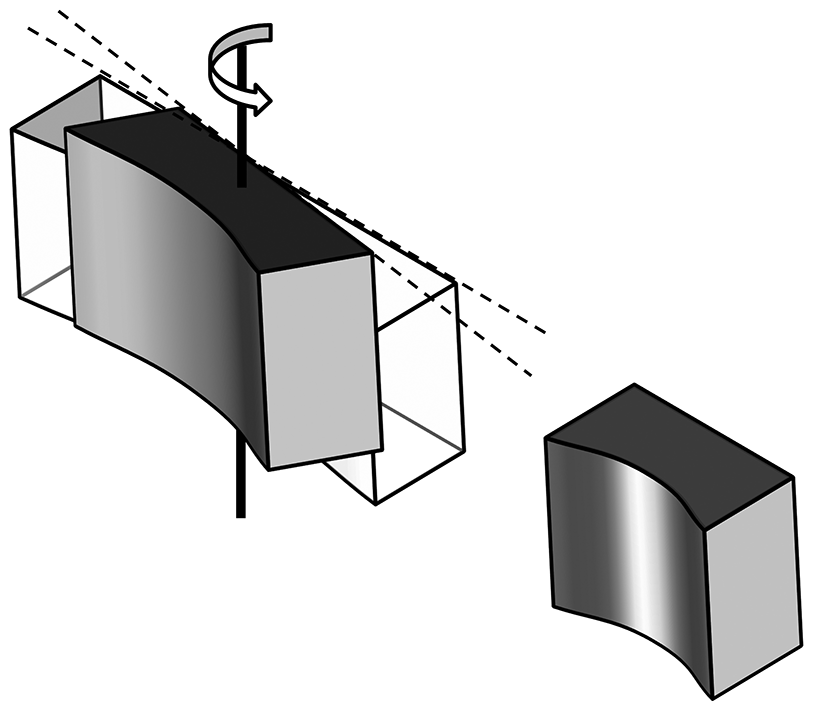）		+/-2	+/-10
並進 （µm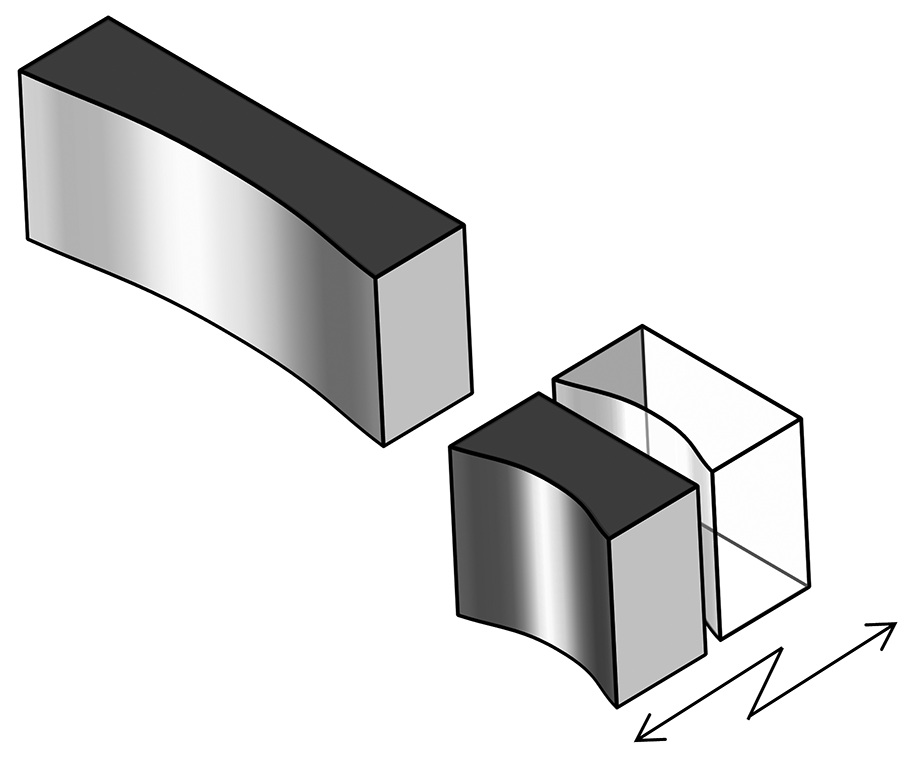）		+/-0.75	+/-1.0
ローリング・直角度 （µrad）		+/-40	+/-50

　このような作製誤差1.5 nmという値は、非常に高精度な非球面ミラーを作製しなければならないことを意味する。この精度を満足するミラーを作製するために、大阪大学山内研究室で開発されたEEM^[10][10] K. Yamauchi, H. Mimura, K. Inagaki and Y. Mori: Rev. Sci. Instrum. 73 (2002) 4028.とスティッチング干渉計^[11,12][11] K. Yamauchi, K. Yamamura, H. Mimura, Y. Sano, A. Saito et al.: Rev. Sci. Instrum. 74 (2003) 2894.
[12] H. Mimura, H. Yumoto, S. Matsuyama, K. Yamamura, Y. Sano et al.: Rev. Sci. Instrum. 76 (2005) 045102.を用いた。EEMは、スラリー（普通はコロイダルシリカと水）をノズルから吐出し、局所的に研磨する手法である。化学的除去作用が特に強く働くため、下地の構造を乱すことなく、原子一層ずつ除去していくことができる。微粒子と基板の接触は基板表面の凸部でしか起こらないため、凸部のみが選択的に除去（自動平滑化作用）される点が非常にユニークである。この結果、X線ミラーに必要な0.2 nm RMS以下の表面粗さが得られるわけである。このスラリー供給をコンピュータ制御することで、優れた表面粗さだけでなく所望の形状をも得ることができる。ただし、その精度はインプットする形状誤差データに依存するため、正確な形状計測データは必要不可欠な情報である。高精度な形状計測を実現するために、スティッチング干渉計を用いた。本手法は、干渉計で計測されたデータを正確につなぎ合わせるというシンプルな手法であるが、現在でもX線ミラー計測において最も有効な手法の一つとして知られている。本手法では約1 nmの形状計測精度を達成できる。これらの方法を駆使して、4枚のX線ミラーを作製した。図3に作製したミラーの形状とその形状誤差を示した。約1 nmの精度で楕円と双曲形状を作製することに成功した。最終的に、マグネトロンスパッタ成膜装置を用いて白金を80 nm成膜し、全反射ミラーとして完成させた。

図3　作製したミラーの形状と形状誤差。

　4枚のミラーをアライメントするシステムは、弾性ヒンジとアクチュエータからなる自作の精密チルトステージや自動ステージから成り、上述した許容誤差以上の精度を持つ。また、4枚のミラーの姿勢をモニターするために、オートコリメータとレーザー変位計からなる形状・角度計測装置が取り付けられている。詳細は省くが、本システムを使い、決められた手順に従ってアライメントしていくことで、許容アライメント精度以上を達成することができた^[8,13][8] S. Matsuyama, N. Kidani, H. Mimura, Y. Sano, Y. Kohmura et al.: Opt. Express 20 (2012) 10310-10319.
[13] S. Matsuyama, Y. Emi, H. Kino, Y. Kohmura, T. Ishikawa et al.: Opt. Express 23 (2015) 9746-9752.。

3. 性能評価実験 －その1－
　開発した結像システムの性能評価実験をSPring-8 BL29XUにて実施した。縮小結像実験^[8,14][8] S. Matsuyama, N. Kidani, H. Mimura, Y. Sano, Y. Kohmura et al.: Opt. Express 20 (2012) 10310-10319.
[14] S. Matsuyama, T. Wakioka, N. Kidani, T. Kimura, H. Mimura et al.: Opt. Lett. 35 (2010) 3583-3585.なども実施したが、今回は拡大結像実験についてのみ説明する。拡大結像実験では、コンデンサー（2枚の平面ミラーと2枚の楕円ミラーから成る）を使って試料を臨界照明し、その後、その散乱光を結像ミラーで45 m下流のX線カメラ（シンチレータ厚：10 µm、実効ピクセルサイズ：3.1 µm）に結像した。図4(b)に得られた結果を示す。コントラスト解析の結果から分解能（コントラストが26.5％以上で可視化された最小構造）は縦90 nmと横120 nmであった^[13][13] S. Matsuyama, Y. Emi, H. Kino, Y. Kohmura, T. Ishikawa et al.: Opt. Express 23 (2015) 9746-9752.。この結果はこの時点で全反射ミラーを使って得られた最小分解能であったが、目標の50 nmには到達できていなかった。原因は、ミラー姿勢の不安定性（温度変化でアライメントが徐々に変化していた？）やアライメントの難しさに起因していると考えた。特にユーザーに使ってもらえる光学系の開発を目指す場合、開発者でも手を焼くシステムというのは到底受け入れられないはずである。

図4　明視野イメージ。(a) SEM、(b) 旧型による結像（露光時間：150秒）、(b) 新型による結像（露光時間：60秒）。X線エネルギー：9.881 keV。試料は電子ビームリソグラフィで作られテストチャート（材質：タンタル、最小線幅：50 nm、厚み：200 nm(b), 500 nm(c)）。

4. 一体型結像ミラーの開発
　比較的開発が容易と考えたこの旧式のAdvanced KBミラー光学系の開発が先行したが、これと並行して、一体型結像ミラーを用いた新型のAdvanced KBミラー光学系の開発を進めた^[15][15] S. Matsuyama, H. Kino, S. Yasuda, Y. Kohmura, H. Okada et al.: Proc. SPIE 9592 (2015) 959208.。一体型結像ミラーは、楕円と双曲が1枚の基板上に作製されたもので、楕円と双曲が完全に固定された結像ミラーである（図5）。楕円と双曲の相対位置は結像特性に大きな影響を与える敏感な箇所である。この部分を固定することができれば、使い勝手と安定性を大幅に改善できる。

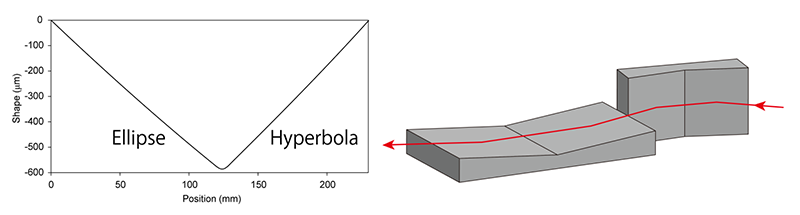
図5　一体型結像ミラーで構築したAdvanced KBミラー。

　ミラー形状は、全体的には非常に急峻なV字状となり（図5左）、その個々の形は楕円と双曲になる。作製法に関する詳細は省くが、様々な計測装置を駆使して、これらの形状を正確に計測し、コンピュータ制御EEMを使って形状修正した。最終的には、1 nm精度でミラーを作製することができ、これは見積もった許容誤差を下回った。このように一体型結像ミラーを正確に作製する技術を確立することができた。

5. 性能評価実験 －その2－
　図4(b)の実験と同じ拡大結像実験を試みた。異なる点は、コンデンサーにポリキャピラリーレンズを使用し、光学素子数をさらに少なくした点である。これによって結像光学系だけでなく光学系全体の安定性を向上させることができた。ビームラインと光学系全体の調整も含めた24時間以内で、50 nm幅のラインアンドスペースを容易に見ることができた。最終的に得られた結果を図4(c)に示す。コントラストの高い明瞭なパターンを得ることができた。これによって、世界で初めて色収差なしかつ50 nmの空間分解能を有する顕微鏡の開発に成功した^[16][16] S. Matsuyama, S. Yasuda, J. Yamada, H. Okada, Y. Kohmura et al.: submitted.。本顕微鏡システムは予想通り非常に安定であった。実験ハッチは振動対策のため空調をOFFにしていたが（室温が0.3℃も変化した）、20時間後であっても像質にほとんど変化がないことを確認している。

6. まとめと応用展開
　高精度な全反射結像ミラーを使うことで、高分解能かつ色収差のない結像型X線顕微鏡を開発した。テストチャートの観察の結果、50 nmの空間分解能を有していることが確認できた。
　本結像光学系は非常に汎用性が高いため、すぐにでも様々な応用が可能である。例えば、高分解能XAFSイメージング、蛍光X線イメージングである。特に蛍光X線イメージングは、色収差がないという特徴を最大限享受できる面白いアプリケーションである。また、本光学系は結像光学系であるが、これを集光光学系として利用しても有用と考える。通常、KBミラーはその入射角が集光径にとても敏感であるが、本結像ミラーは視野が広いため入射角誤差の許容度は大きい（±80 µrad）。そのため、本光学系を集光光学系として用いれば、長期間集光径を崩すことのない高い安定性を持つ集光システムを開発できる。その他、共鳴非弾性散乱用のイメージングスペクトロメータを構成する光学系^[17][17] T. Warwick, Y. De Chuang, D. L. Voronov and H. A. Padmore: J. Synchrotron Radiat. 21 (2014) 736-743.として用いるなども提案されている。
　今後、次世代光源（SPring-8-II、SLiT-Jなど）の登場に伴い、ユーザーが光学系に期待する性能も格段に高まると予想される。本光学系はきっとそのようなユーザーの期待に応えるものになると確信できる。また、さらなる改良をどんどん進めていこうと考えている。

謝辞
　共同研究者である大阪大学 山内和人教授、安田周平氏、山田純平氏、株式会社ジェイテックコーポレーション 岡田浩巳氏、理化学研究所 石川哲也センター長、矢橋牧名グループディレクター、香村芳樹ユニットリーダーに深く感謝します。BL29XUでの実験は理化学研究所の手厚い支援の下実施されました。

参考文献
[1] T.-Y. Chen, Y.-T. Chen, C.-L. Wang, I. M. Kempson, W.-K. Lee et al.: Opt. Express 19 (2011) 19919-19924.
[2] Y. Suzuki, A. Takeuchi, H. Takenaka and I. Okada: X-Ray Opt. Instrum. 2010 (2010) 1.
[3] C. G. Schroer, O. Kurapova, J. Patommel, P. Boye, J. Feldkamp et al.: Appl. Phys. Lett. 87 (2005) 124103.
[4] R. Kodama, N. Ikeda, Y. Kato, Y. Katori, T. Iwai et al.: Opt. Lett. 21 (1996) 1321-1323.
[5] H. Wolter: Ann. Phys. 445 (1952) 94-114.
[6] P. Kirkpatrick and A. V. Baez: J. Opt. Soc. Am. 38 (1948) 766-774.
[7] S. Matsuyama, M. Fujii and K. Yamauchi: Nucl. Instr. Meth. Phys. Res. 616 (2010) 241-245.
[8] S. Matsuyama, N. Kidani, H. Mimura, Y. Sano, Y. Kohmura et al.: Opt. Express 20 (2012) 10310-10319.
[9] H. Mimura, S. Handa, T. Kimura, H. Yumoto, D. Yamakawa et al.: Nat. Phys. 6 (2010) 122-125.
[10] K. Yamauchi, H. Mimura, K. Inagaki and Y. Mori: Rev. Sci. Instrum. 73 (2002) 4028.
[11] K. Yamauchi, K. Yamamura, H. Mimura, Y. Sano, A. Saito et al.: Rev. Sci. Instrum. 74 (2003) 2894.
[12] H. Mimura, H. Yumoto, S. Matsuyama, K. Yamamura, Y. Sano et al.: Rev. Sci. Instrum. 76 (2005) 045102.
[13] S. Matsuyama, Y. Emi, H. Kino, Y. Kohmura, T. Ishikawa et al.: Opt. Express 23 (2015) 9746-9752.
[14] S. Matsuyama, T. Wakioka, N. Kidani, T. Kimura, H. Mimura et al.: Opt. Lett. 35 (2010) 3583-3585.
[15] S. Matsuyama, H. Kino, S. Yasuda, Y. Kohmura, H. Okada et al.: Proc. SPIE 9592 (2015) 959208.
[16] S. Matsuyama, S. Yasuda, J. Yamada, H. Okada, Y. Kohmura et al.: submitted.
[17] T. Warwick, Y. De Chuang, D. L. Voronov and H. A. Padmore: J. Synchrotron Radiat. 21 (2014) 736-743.

松山　智至　MATSUYAMA Satoshi
大阪大学大学院　工学研究科
〒565-0871　大阪府吹田市山田丘2-1
TEL : 06-6879-7286
e-mail : matsuyama@prec.eng.osaka-u.ac.jp