Volume 15, No.1 Pages 3 - 9

1. はじめに

　唐突な書き出しで恐縮だが、現代科学における重要な未解決問題は何だろう。

　ハイテク、ナノテク全盛の今日、新規問題の探索よりは、ともすれば我々は蓄積が生かせる専門分野の改良や向上に眼を向けがちである。しかし科学には、まだまだ未解決の問題が数多く残っている。

　2005年Scienceは、その創刊125周年にちなみ、自然科学の125の未解決問題を掲載した^[1][1] Science 309 (2005) 78-102.。宇宙は何からできているのか、究極の統一理論はあるか、超伝導体の転移温度はどこまで上がるのか、人間は何歳まで生きられるのか・・・などなど。みなさんはどうお考えだろうか。各々が日々取り組んでいる専門を離れて、このようなことに思いを馳せるのもたまにはよいだろう。

　残念ながら、125の問題の中に「非平衡統計力学」はとりあげられていない。これは、熱平衡や不可逆変化という概念がわかりにくいことを反映している。加速度やエネルギーは、たとえ話を使うと子どもにも明快に理解できる。しかし、熱機関やエントロピー増大則は研究者を目指す者でさえ、なかなか取っ付きにくい。実際、カルノーやボルツマンは、学説の真価を学界に理解される事なく不遇にこの世を去った。著者の一人は、中学生の頃、生物は『負のエントロピー』を食べて非平衡状態を保つという学説を読み衝撃を受けたが、その意味を理解できたとは言い難い。

　Scienceの125もの未解決問題のうち、半数以上が生物・生命に関連しており、生物が典型的な非平衡系であることを考えたとき、指摘されなかった未解決問題の重要性に気がつく。生物科学の根本的な理解のためには「非平衡統計力学」の深化は避けては通れない。熱や粒子の定常的な流れがあるマクロな系は非平衡系の典型である。それがどのようにミクロな量と関係づけられるかという問題は、最初にボルツマンによって考察され、統計力学の黎明期からその重要性はすでに認識され、議論点ともなっていた^[2][2] ボルツマン方程式については、たとえば、山下次郎、長谷川彰訳、J. M. ザイマン著「固体物性論の基礎」（丸善、1976）第7章.。

　非平衡統計力学における揺動散逸定理^[3][3] R. Kubo: J. Phys. Soc. Jpn. 12 (1957) 570-586.は我国が誇るノーベル賞級の成果である。これは平衡からわずかに離れた領域の線形応答を定量的に記述できる優れた理論であり、非平衡を特徴づける散逸量が熱平衡状態の熱力学変数のゆらぎとフーリエ変換で結びつけられるという美しい形式を持つ。この定理は、記述している非平衡系が、ある平衡状態へ向かって緩和しているときに成り立つ。

　しかし、緩和以外の非平衡系は未解決のまま残されている。自然科学は、自然の精緻な観測と分析による定式化とその理解により発展する。非平衡統計力学を更に発展させるためには、本質的な非平衡現象を詳細に観測する必要がある。しかし、非平衡系である流体や生体の観測結果を分析し定式化することは容易ではない。我々は発想を少し変え、生体系のミニマルモデルを固体中の非平衡な電子に求めた。固体中の電子には、電流、電場という非平衡状態を生み出しえる基礎量があり、その振る舞いを物理学の知見に基づいて分析し定式化可能であるからである。さらには、その電気・磁気特性を利用し新規な機能性素子を作り出すという夢も抱いているからでもある。

2. 有機サイリスタ

　本稿で取り上げる有機サイリスタは、電子系が本質的な非平衡現象を示す稀有な例である^[4,5][4] K. Inagaki, I. Terasaki, H. Mori and T. Mori : J. Phys. Soc. Jpn. 73 (2004) 3364-3369.
[5] F. Sawano et al.: Nature 437 (2005) 522-524.。この物質については数年前に、本誌で報告させていただいた^[6][6] 寺崎一郎、池田直：SPring-8利用者情報 11 (2006) 17-21.。また、他誌にもいくつか解説記事を書かせていただいた^[7,8][7] 寺崎一郎：固体物理 40 (2005) 899-906.
[8] 森初果、寺崎一郎、森健彦：化学 61、2 (2006) 12-16.。本稿では、それらの記事以降にSPring-8で行われた研究を中心にその面白さを平易に解説しよう。具体的な成果を3節で示す前に、ここではその前提となる予備知識を簡潔に紹介する。

　有機サイリスタはθ-(BEDT-TTF)₂CsZn(SCN)₄という化学式で表される分子性導体である^[9][9] H. Mori, S. Tanaka,T. Mori : Phys. Rev. B 57 (1998) 12023-12029.。その構造は、図1(a)に示すようにBEDT-TTF（ビスエチレンジチオ・テトラチアフルバレン）分子がスタックした伝導層が、CsZn(SCN)₄層と交互に積層した層状物質である。Cs、Zn、SCNはそれぞれ+1、+2、−1価であり、BEDT-TTFの形式価数は+0.5となる。すなわち2分子あたり+1個のホールが存在し、自由キャリアとしてBEDT-TTF分子の分子軌道を伝導して電気を運ぶ。化学式の前に書かれたギリシャ文字θはBEDT-TTF分子のパッキングの仕方を指定しており、θ型は図1(b)に示すような配置である。BEDT-TTF分子を一つの原子に置き換えると、θ型は箱に詰められたタバコを上から見たような構造となり、物性物理学や統計力学で精力的に研究されている「三角格子」と等価になる。

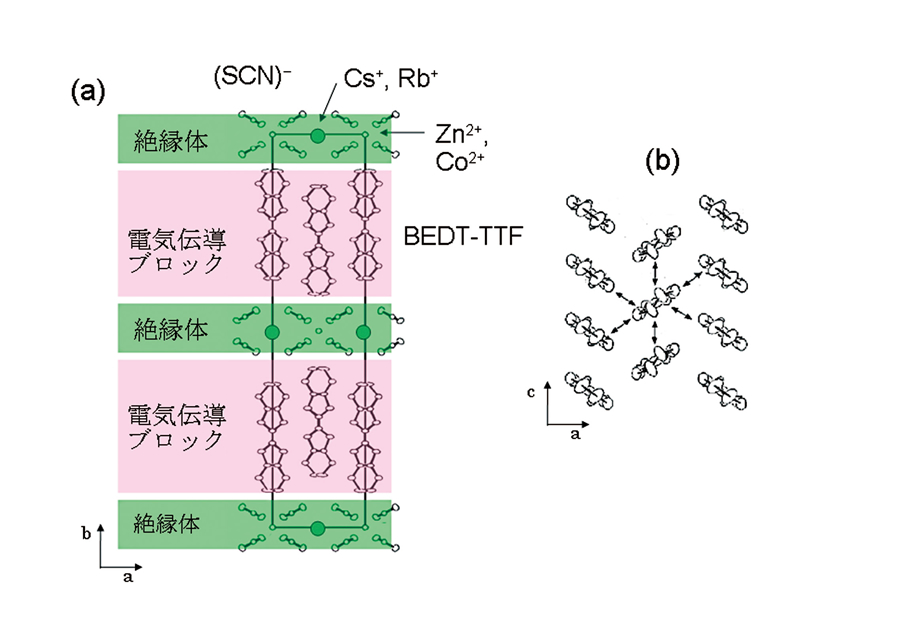
図1　有機サイリスタθ-(BEDT-TTF)₂CsZn(SCN)₄の結晶構造。(a) 層状構造、(b) BEDT-TTF層（伝導層）の中でのBEDT-TTFのパッキング配置。

　有機サイリスタの中を運動するホール同士には強いクーロン斥力が働き、ホールは互いの距離を等間隔に保って低温で凍結する。この「電子の氷」は、電荷秩序とか電荷整列と呼ばれる電子相のひとつである^[10][10] 妹尾仁嗣、鹿野田一司、福山秀敏：日本物理学会誌 58 (2003) 801-808.。有機サイリスタの場合、2分子に1個のホールが存在するので、各格子点に白黒の碁石を交互に置いて得られる模様が電荷秩序である。ところが三角格子では、単位胞の中で白か黒のどちらかの碁石が必ず1つ多くなる。これが、四角格子ならば交互に白黒の碁石を置いた状態が安定となる。世間の三角関係と同じく、固体の中の三角関係もきれいには解けない。その結果、様々なパターンの電荷秩序がエネルギー的に拮抗する^[11,12][11] 森健彦：日本物理学会誌 61 (2006) 516-520.
[12] 渡部洋、小形正男：固体物理 42 (2007) 185-191.。

　先行研究によって、有機サイリスタでは2つの波数q₁ = (2/3, 0, 1/3)、q₂ = (0, 0, 1/2)で指定される2種類の電荷秩序が低温で共存することがわかっていた^[13][13] M. Watanabe, Y. Nogami, K. Ohshima, H. Mori and S. Tanaka: J. Phys. Soc. Jpn. 68 (1999) 2654-2663.。図2(a)にそのデータを示す。20 KにおけるX線回折パターンに明瞭な2つのピークが観測されている。その半値幅から見積もられる秩序のサイズは10 nm程度であり、より温度を下げても2つのピークが一つになることも、幅が狭くなることもない。このことは2種類の電荷秩序がナノスケールで混ざりあいながら共存していることを示唆している。実際、この系の帯磁率や比熱といった熱力学量にはほとんど異常が見られず、電荷秩序の共存状態は熱力学的な相転移を経由せずに実現した、ガラスのようなやや不安定かつ非平衡な状態である。

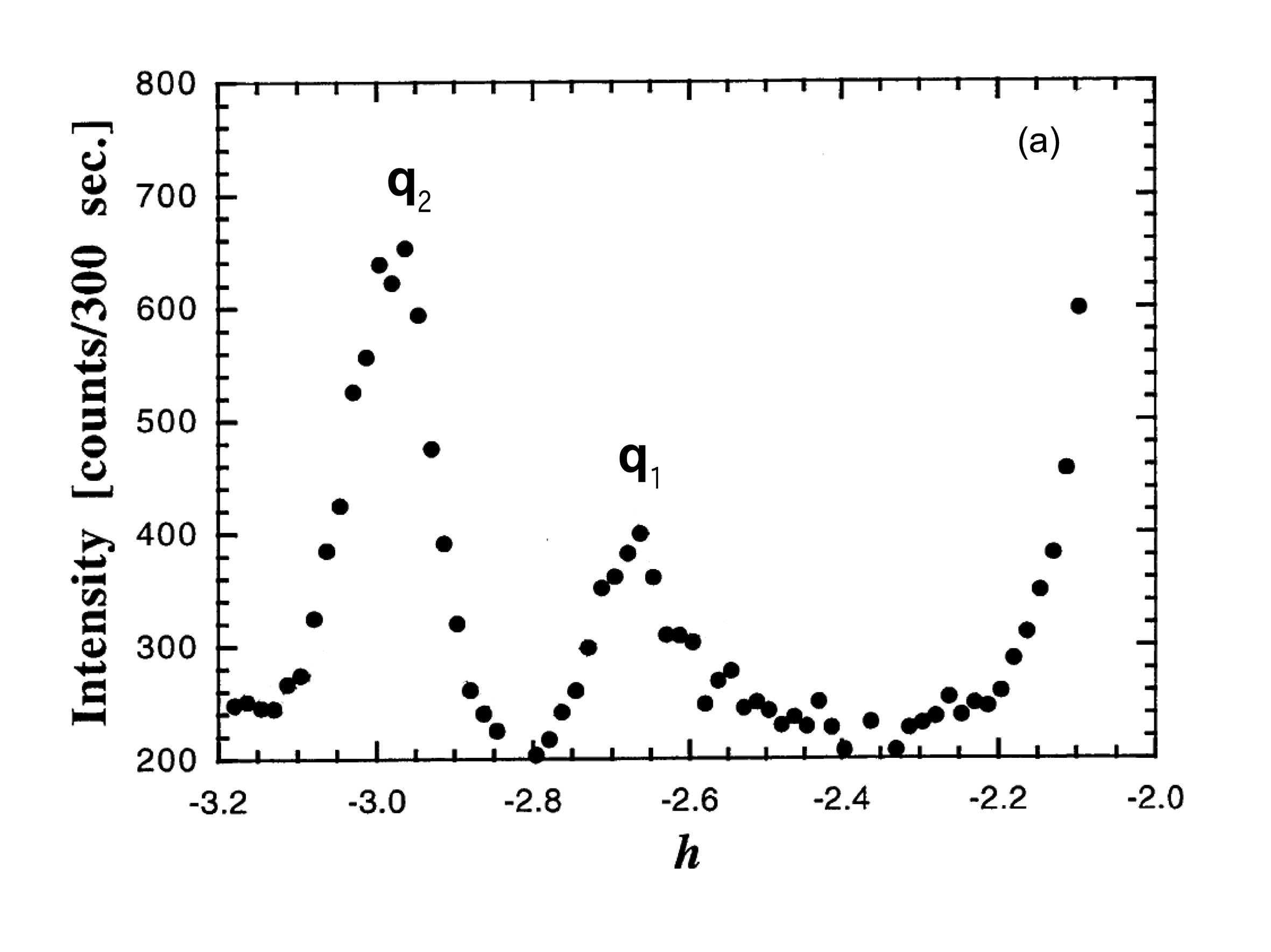
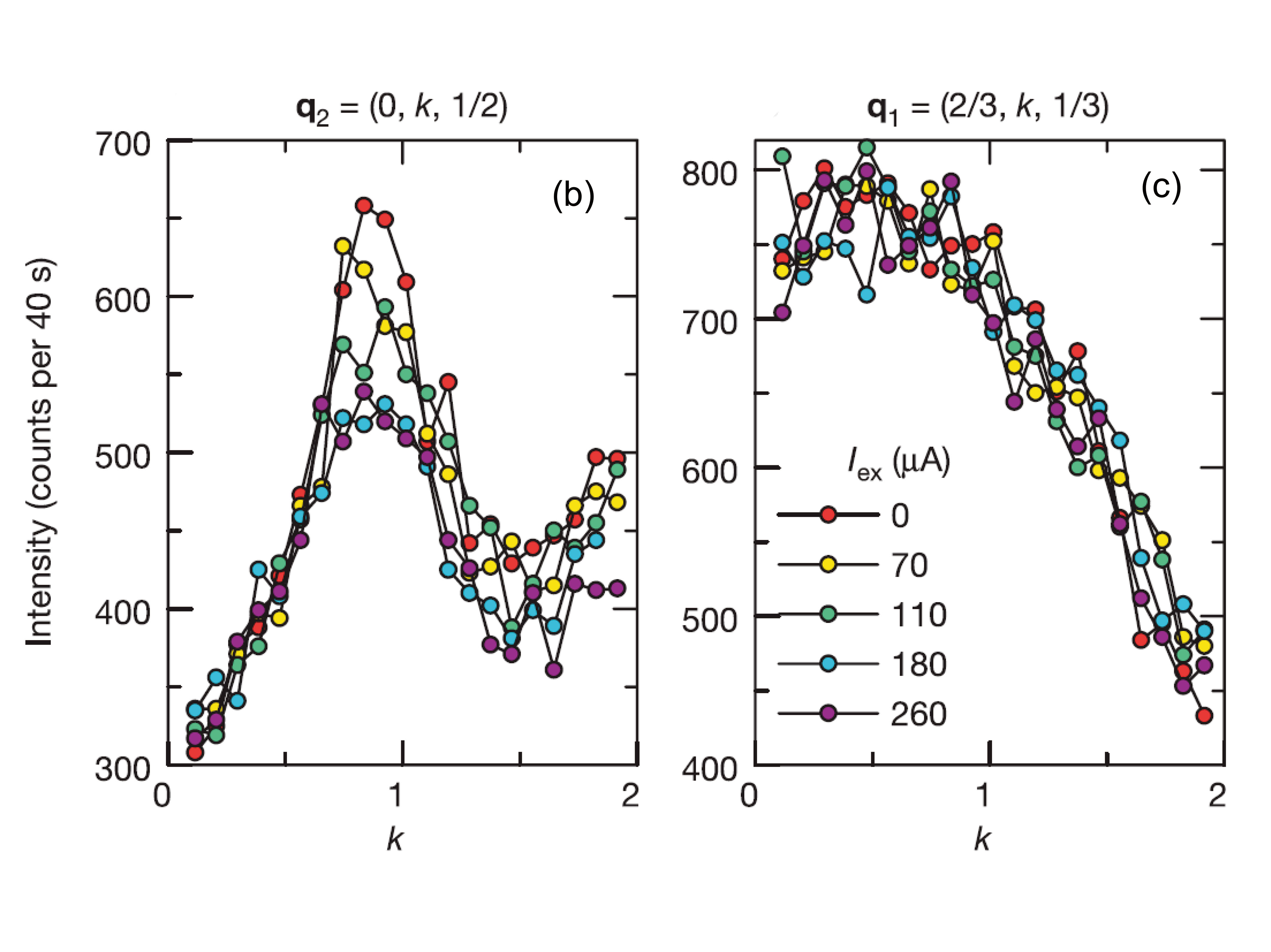
図2　有機サイリスタの低温X線散漫散乱。(a) 20 Kにおける散漫散乱。q₁、q₂で指定される2つの電荷秩序からの散漫散乱が同時に観測されている。横軸は、a^＊c^＊平面（BEDT-TTF層の面内方向）で2つの散漫散乱を結ぶ方向の逆格子位置を表す。(b) q₂散漫散乱の依存性。(c) q₁散漫散乱の電流依存性。(b)、(c)の横軸は、b^＊軸（BEDT-TTF層の面間方向）の逆格子位置を表す。q₂が面間方向にもピークを持つのに対して、q₁は面間方向にほぼフラットな強度を持つ。このことは、前者が擬3次元的な短距離秩序、後者が2次元的な短距離秩序を示している。

　このq₁とq₂が共存した状態で電流を流すと、q₂ピークだけが抑制される。その様子を図2(b)、(c)に示す^[5][5] F. Sawano et al.: Nature 437 (2005) 522-524.。電流は電子（ホール）の流れにほかならないから、この結果はq₂型の電子の氷が電流によって融解したように見える。冬の寒い日に、池の水は凍るが、川の水は凍らない。水道管の凍結を防ぐために少しだけ蛇口をゆるめておくという、北国では必須の知恵はこの経験に由来する。図2の結果は、水と同じことを電子が見せたのではなかろうか。そしてそれは、電子が示す本質的な非平衡現象ではなかろうか。

　電流によるq₂型の電荷秩序の抑制は、電気伝導にも大きな影響を及ぼす。やはり先行研究で、q₂型の電荷秩序が系の金属−絶縁体転移と関連していることがわかっており、q₂とともに抵抗率は急上昇する^[9][9] H. Mori, S. Tanaka,T. Mori : Phys. Rev. B 57 (1998) 12023-12029.。したがって、電流を印加することでq₂の成長が抑えられるならば、この物質の抵抗率は電流とともに急激に低下する非線形伝導を示すはずである。実際、そのような巨大な非線形伝導が実験で観測できる。図3に有機サイリスタの抵抗V_sample/I_exおよび電圧V_sampleの電流依存性を示す。この電圧－電流特性がサイリスタ素子のそれと同じ形なので、我々はこの物質を有機サイリスタと呼んだ。

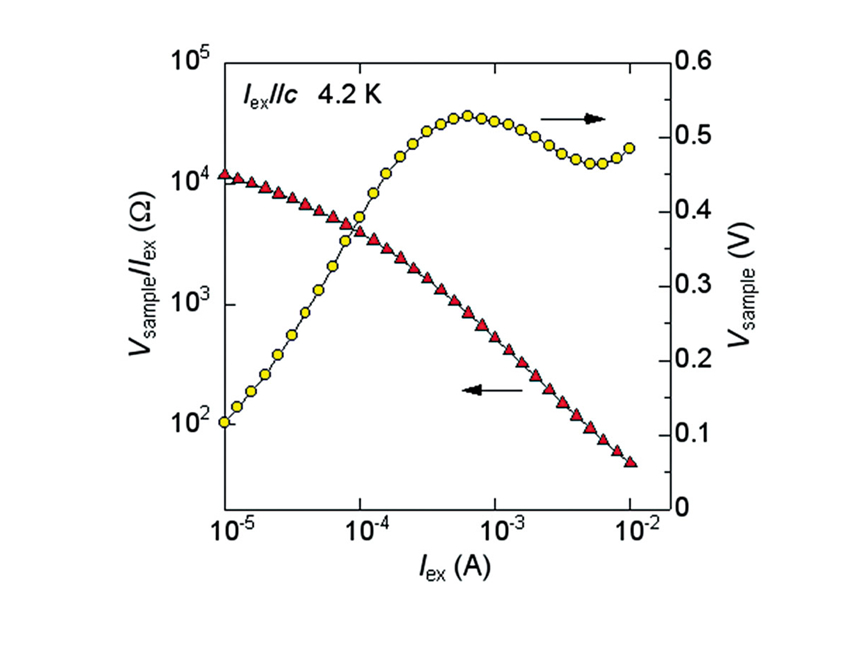
図3　有機サイリスタの4.2 Kにおける非線形伝導。抵抗と電圧降下の電流依存性。

3. SPring-8が明らかにした新現象

　さて、既に述べたように、有機サイリスタの研究は、「流れる電子がどのようにして電子の氷を溶かすのか」を明らかにすることに集約される。我々はSPring-8の長期利用課題「共存する電荷秩序が作る機能と構造」として、BL02B1の7軸回折計を武器にこの問題に挑んだ。BL02B1は、単結晶のX線回折実験を行うステーションである。X線振動写真を撮影する大型湾曲IPカメラと7軸回折計が設置されている。ここでは、単結晶構造解析と並び、単結晶試料の逆格子空間内の超格子構造の解析や、あるいは高エネルギーX線を用いた回折実験による材料評価などが行われている。SPring-8の中にある回折計としては汎用性の高い測定装置群である。

　図4にその測定セットアップの一例を示す。試料マウントの周辺については文献^[6][6] 寺崎一郎、池田直：SPring-8利用者情報 11 (2006) 17-21.を参照いただきたい。SPring-8は大変な高輝度光源である。このため、計測効率が悪いと有機物の放射線ダメージは深刻になる。これを回避するために検出器にはPILATUS（pixel apparatus for the Swiss Light Source）^[14][14] http://detector.spring8.or.jp/pixel/と呼ばれる2次元デテクタを実装し、複数のブラッグ反射を含む領域を同時計測している。また電流の効果を見るために、ミリ秒オーダーの時間分解測定を行い、q₁、q₂、ブラッグ反射の強度を時間、電流、温度の関数として精密に計測した。本研究で使用したBL02B1の7軸回折計は、逆格子空間の測定精度は格子定数のppmオーダーの変化をとらえられる分解能を持ち、ブラッグ反射の10000分の1にも満たない散漫散乱を検出できる高いSN比を持つ。この特徴は、本研究の実験で存分に活かされた。

図4　SPring-8のBL02B1にセットアップされた実験装置の一例。

　まず我々が取りかかったことは図2、3の結果が単なるジュール熱では決して説明できないことを明らかにすることだった。「試料の抵抗を測定する時に、決して大きな電流を流してはいけない。」我々は厳しくそう教えられてきた。大きな電流を通電すればジュール熱による自己発熱が生じ、望まない温度上昇が試料に生じる。当然、電荷秩序は温度が上がっても消失するので、自己発熱が深刻な場合は電流の効果は単に試料の温度を上げただけのことで新発見でも何でもない。有機サイリスタは4 K付近の低温領域で動作するので、わずかな熱量で簡単に試料温度は上昇し得る。我々は注意深く自己発熱の効果を見積り、複数の方法で温度上昇の上限を調べた。その詳細は多分に専門的なので本稿では省略するが、自己発熱の影響は、電流そのものによる効果よりもずっとずっと小さいことがわかった。興味ある読者は文献^[15,16,17][15]M. Watanabe et al.: J. Phys. Soc. Jpn. 77 (2008) 065004.
[16] T. Ito et al.: Europhys Lett. 84 (2008) 26002.
[17] F. Sawano et al.: J. Phys. Soc. Jpn. 78 (2009) 024714.を参照されたい。

　次に我々は、電流によるq₂ピークの抑制が本質的な非平衡現象であることをはっきりと示すために、周辺物質であるθ-(BEDT-TTF)₂RbZn(SCN)₄に注目した。この物質は、190 Kでq₂型の電荷秩序転移を示し絶縁体となる^[9,10][9] H. Mori, S. Tanaka,T. Mori : Phys. Rev. B 57 (1998) 12023-12029.
[10] 妹尾仁嗣、鹿野田一司、福山秀敏：日本物理学会誌 58 (2003) 801-808.。この転移が1次転移であることを利用し、転移温度付近を急冷すれば、過冷却状態を作ることができる。この状態は、様々な点で有機サイリスタで実現しているq₁、q₂の共存状態と類似しており、比較により知見を深める事ができる。図5にその様子を示す^[18][18] Y. Nogami et al.: J. Phys. Soc. Jpn. (in press).。2種類の電荷秩序q₁' = (1/3, 0, 1/4)とq₂が同時に観測されている。この共存状態においては、自己発熱は安定相であるq₂の成長を促進させ、電子の流れはq₂を抑制する方向に働く。有機サイリスタの場合には、両者がともにq₂を抑制する方向に働いたのと対照的であることに注意してほしい。実際の測定では、明らかにq₂ピークは電流で抑制されている。これはジュール熱によるq₂相の成長に打ち勝って、電子の流れがq₂相を壊していることを示している。我々が予想したように、この現象は本質的な非平衡現象であると思ってよさそうだ。

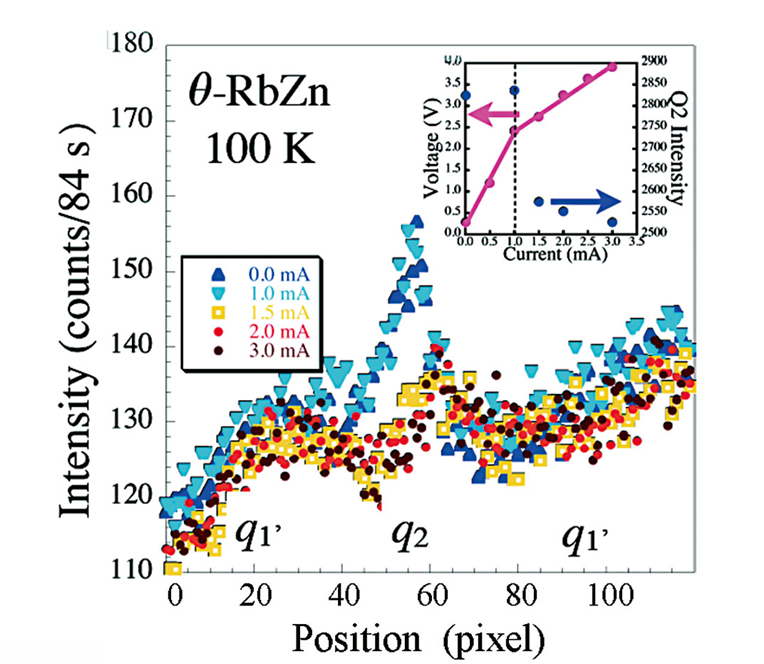
図5　周辺物質θ-(BEDT-TTF)₂RbZn(SCN)₄の急冷相の100 KにおけるX線散漫散乱。q₁'、q₂で指定される2つの散漫散乱が観測され、電流とともにq₂散乱が減少している。挿入図に、電圧降下とq₂散乱強度の電流依存性を示す。

　3番めの成果は、電流によって結晶の体積を変化させたことである。これは通常の圧電材料が電圧によって駆動されることと対照的である。もちろんそのしくみも全く異なっており、次のようなものである。ホールが電荷秩序を形成して凍結すると、さらにクーロン斥力を下げようとしてわずかに回転する。したがって、電流によってq₂が抑制されるならば、分子の回転もまた抑えられる。

　我々はブラッグ反射が電流によってどのように変化するかを精密に測定した。図6にa軸長、c軸長の電流による変化を示す。両方の軸ともに電流量とほぼ線形に変化していることがわかる。この結果は、有機サイリスタの体積が電流で変わることを示している。体積は代表的な熱力学量であり、それが電流という非平衡量の関数で書けるということは、電流を変数とする「自由エネルギー」のような量の存在を我々に予感させる。ちなみに、電流による軸長の変化は巨大である。たとえば、4 mAの電流の印加に対して電圧降下は0.5 V程度であるが、このときのc軸長の変化0.1 pmは、1 V/cmあたりの歪みΔL/Lが100 ppmであることを示す。この値は典型的な逆圧電効果の数千から数万倍の大きさである。典型的な圧電材料であるPZTの圧電定数は10^-10 m/Vのオーダーであるから、1 V/cmでΔL/Lは0.01 ppmしか変化しない^[19][19] 国立天文台編：理科年表（丸善）.。このような大きな値がなぜ得られたのかといえば、電流で電子相そのものを制御したからである。圧電材料では、外部電場の方向に相対的に強誘電ドメインの割合が伸長することで歪みが生じる。電場は、強誘電相そのものを作り出しているわけでは決してない。

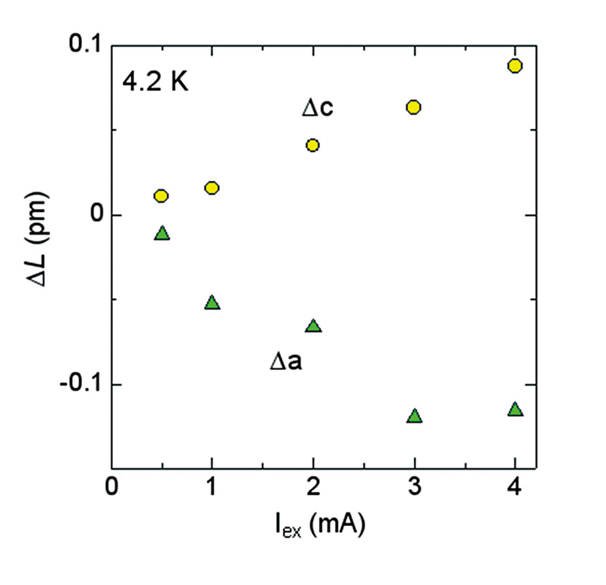
図6　格子定数の電流依存性。測定温度は10 K。

　4番めの成果は、q₂ピークやブラッグ反射の時間変化の計測である。図7に観測結果の一例を示す。q₂ピークもブラッグ反射も電流の印加直後から変化している。この図の場合、ブラッグ反射は、いま計測している領域から逃げてゆく方向に動いたため強度が減ったように観測されている。その時間依存性には、印加直後10 msまでの急速な変化とそれに続く200 msまでの緩慢な変化が見て取れる。直感的には、前者が電荷秩序の融解、後者が分子の回転の解消に対応しているように見える。一方、電流を切ったときの回復過程に注目すると、その緩和は遅い緩和しかないように見える。少し専門的になるがボルツマン方程式に基づく電気伝導理論では、電場を加えた時の緩和と切ったときの緩和は同じ緩和時間を持つ。これは、波数pからqへの散乱とqからpへの散乱が時間反転の対称性を持つという仮定（微視的可逆性の仮定）に基づく^[2][2] ボルツマン方程式については、たとえば、山下次郎、長谷川彰訳、J. M. ザイマン著「固体物性論の基礎」（丸善、1976）第7章.。逆に言えば図7の結果は、この現象ではその仮定が破れていることを示唆しており、本質的な非平衡性の一側面を表していると言える。

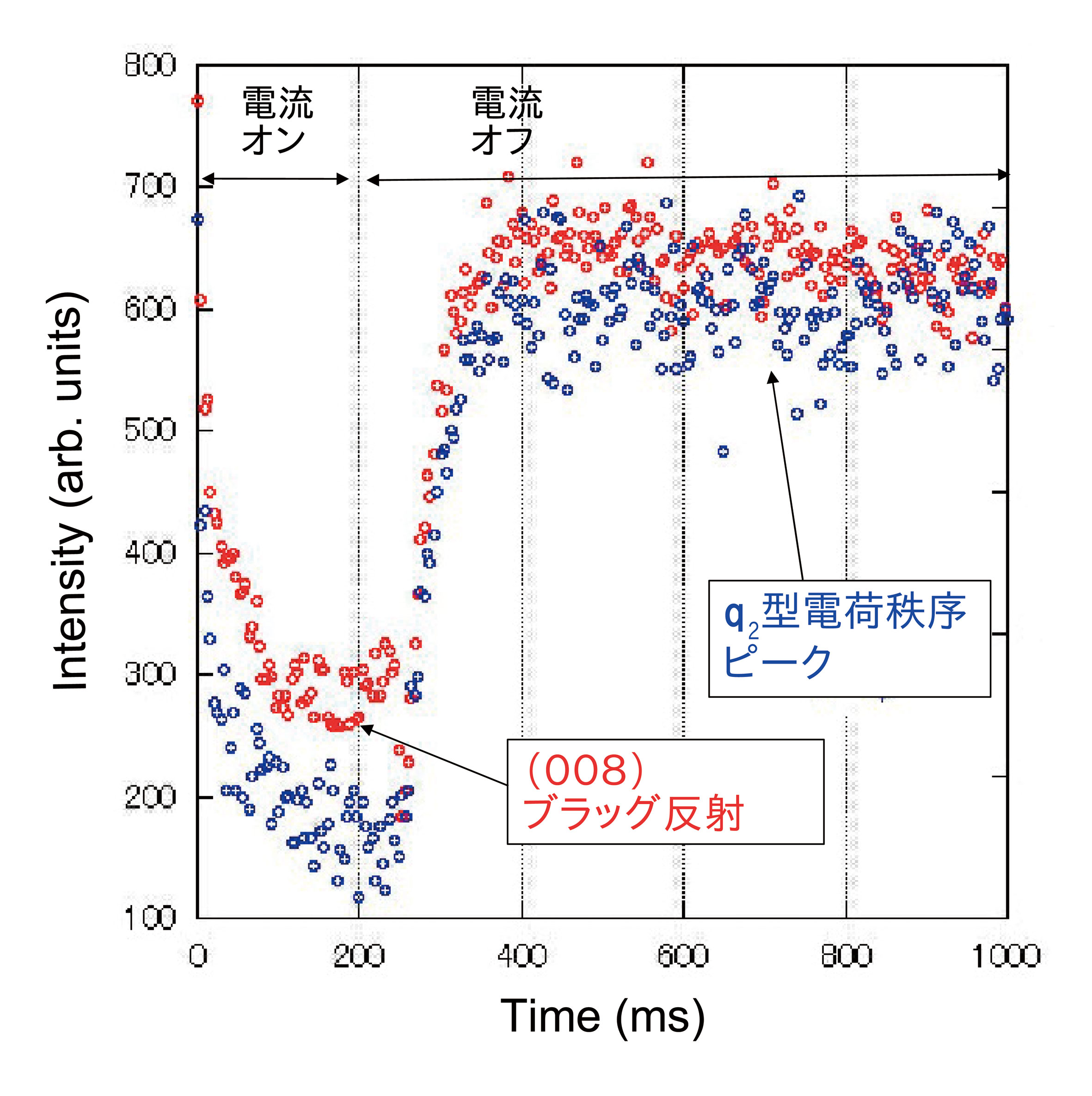
図7　q₂散漫散乱およびブラッグ反射の電流印加にともなう時間変化。200 msで電流をオフにした。

4．メカニズムの解明

　前節でみたとおり我々は、電流によるq₂ピークの抑制が本質的な非平衡効果であって、電流が良い制御変数であることを実験的に明らかにした。鯵坂らは、昨年この現象をよく説明する非平衡相転移の理論を提案した^[20][20] S. Ajisaka, H. Nishimura, S. Tasaki and I. Terasaki : Prog. Theor. Phys. 121 (2009) 1289-1319.。理論の詳細な解説には高度な場の理論を必要とし、本稿の範囲を越える。ここではその結果だけをかいつまんで紹介しよう。

　いま、左右2つの熱浴にはさまれた電気伝導体を考える。電流を左から右に流すということは、左の熱浴からホールを右の熱浴から電子を注入することに対応する。正味の電荷の増分はゼロだが流れがあるという状態である。鯵坂らは、伝導体として電荷秩序相（正確には電荷密度波相またはパイエルス転移相）を考え、過剰に注入された電子とホールによってどのように電荷秩序ギャップが変化するかを、ギャップが満たす運動方程式の解として調べた。

　計算の結果を定性的に述べると以下のようになる。ギャップの大きさは、ギャップ以下のエネルギーに凝縮した基底状態電子と、ギャップの上に熱励起された電子・ホール（準粒子）の相互作用で決まる。転移温度近くではギャップがほとんどゼロですべての電子は準粒子として存在する。一方、絶対零度近くでは、ギャップは成長しほぼ一定値をとり、準粒子はほとんどいない。もしも低温において過剰に準粒子が注入されたなら、ギャップの上の準粒子にとっては、あたかも温度が高くなったように感じるだろう。そこで、ギャップは準粒子の過剰な数とバランスするように小さくなる。過剰に注入される準粒子の数は電流に比例するから、電流とともにギャップは小さくなるはずである。

　図8に理論計算と実験結果の比較を示す^[21][21] I. Terasaki et al.: Physica B (in press).。紙面の都合でここでその詳細は述べないが、抵抗率の温度依存性から見積もることができる活性化エネルギーを電流を変えながら測定すると、図の印で示したデータを得ることができる。またq₂ピークの積分強度の平方根を印を同時にプロットした。2つのデータは比較的よい一致を示している。理論は何らかの相転移を仮定しているから転移温度を持っているが、実験には明確な転移温度がない（2つの電荷秩序の共存状態によって熱力学的相転移はない）ので、これをパラメータとしてデータをフィットした。実験と理論との整合性はよい。

　以上の結果から、「流れる電子がどのように電子の氷を溶かすのか」の答えは次のようになろう。この電子の氷においては、秩序の強度（直感的には氷の大きさやできかた）は準粒子との相互作用で決まる。水の結晶の場合は体積分率がX線の散乱強度に比例しているのに対して、電荷秩序の場合は秩序の強度の自乗と体積分率の積に比例する。電流は準粒子を過剰に生成する効果として秩序の強度を低下させることによってq₂の散乱強度を抑制する。

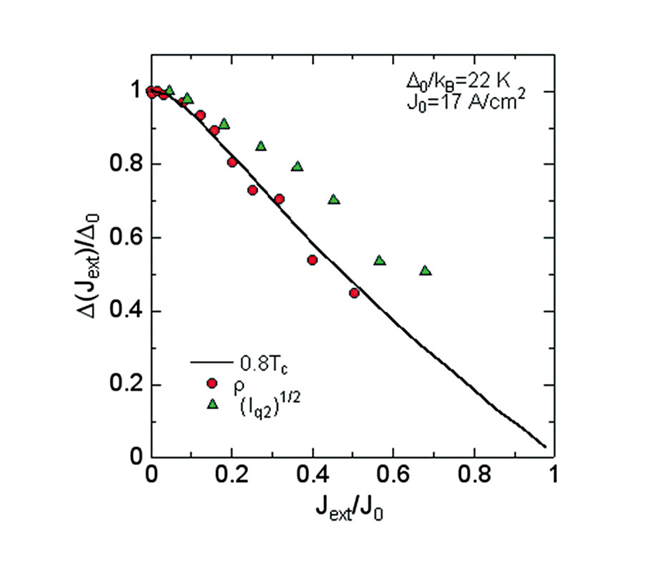
図8　非平衡相転移の理論との比較。電荷秩序のエネルギーギャップを電流の関数として示す。実線は理論曲線、は非線形抵抗から求めたギャップ、 はq₂ピークの積分強度の平方根に対応する。

5．まとめにかえて

　本稿では、有機サイリスタで見られる非平衡状態の物理を平易に解説した。電荷秩序という電子相が、どのように電流によって抑制されるかをSPring-8での精密測定、非線形伝導、非平衡統計理論から調べた。そしてこの系が、非平衡相転移の例としてよく記述できることを見出した。非平衡統計力学の進歩には、典型物質が不可欠である。ちょうど平衡状態の熱・統計力学が理想気体を典型物質として完成したように。有機サイリスタがそのような物質、あるいはそのような物質に行き着くきっかけとなる物質となればと信じ、研究を進めたい。

　とはいえこれで、すべてが明らかになったというわけではない。有機サイリスタにおける2つの電荷秩序の共存状態、電荷秩序のナノサイズドメインがガラス状に凍結した状態がどのようにこの非平衡現象に関係しているのかはまだ明らかになっていない。X線回折は系の規則構造のよいプローブであるが、実空間の不均一情報には別のプローブが必要となる。我々は、長期利用課題の成果を基にして、BL43IRの赤外顕微分光装置を用いた電荷秩序の不均一構造の直接測定を始めた。結果がまとまるまでにはまだ時間がかかるが、本物質の不均一構造と非平衡性の関係を明らかにしたいと思っている。

謝辞

　本研究は、渡邉真史、山本健一郎、伊藤崇芳、花咲徳亮、池田直、杉本邦久、水牧仁一朗、豊川秀訓、大隅寛幸、野田幸男、森初果、森健彦、稲垣宏一、澤野文章、須子友博、稲田太一、鯵坂繁、田崎秀一各氏との共同研究である。赤外顕微分光については、森脇太郎、池本夕佳、佐々木孝彦、大西祐也、高田昌樹各氏との共同研究である。本研究は科学研究補助費（17340114、16076213、21540323）、21世紀COEプログラムの支援を受けた。

参考文献

[1] Science 309 (2005) 78-102.

[2] ボルツマン方程式については、たとえば、山下次郎、長谷川彰訳、J. M. ザイマン著「固体物性論の基礎」（丸善、1976）第7章.

[3] R. Kubo: J. Phys. Soc. Jpn. 12 (1957) 570-586.

[4] K. Inagaki, I. Terasaki, H. Mori and T. Mori : J. Phys. Soc. Jpn. 73 (2004) 3364-3369.

[5] F. Sawano et al.: Nature 437 (2005) 522-524.

[6] 寺崎一郎、池田直：SPring-8利用者情報 11 (2006) 17-21.

[7] 寺崎一郎：固体物理 40 (2005) 899-906.

[8] 森初果、寺崎一郎、森健彦：化学 61、2 (2006) 12-16.

[9] H. Mori, S. Tanaka,T. Mori : Phys. Rev. B 57 (1998) 12023-12029.

[10] 妹尾仁嗣、鹿野田一司、福山秀敏：日本物理学会誌 58 (2003) 801-808.

[11] 森健彦：日本物理学会誌 61 (2006) 516-520.

[12] 渡部洋、小形正男：固体物理 42 (2007) 185-191.

[13] M. Watanabe, Y. Nogami, K. Ohshima, H. Mori and S. Tanaka: J. Phys. Soc. Jpn. 68 (1999) 2654-2663.

[14] http://detector.spring8.or.jp/pixel/

[15] M. Watanabe et al.: J. Phys. Soc. Jpn. 77 (2008) 065004.

[16] T. Ito et al.: Europhys Lett. 84 (2008) 26002.

[17] F. Sawano et al.: J. Phys. Soc. Jpn. 78 (2009) 024714.

[18] Y. Nogami et al.: J. Phys. Soc. Jpn. (in press).

[19] 国立天文台編：理科年表（丸善）.

[20] S. Ajisaka, H. Nishimura, S. Tasaki and I. Terasaki : Prog. Theor. Phys. 121 (2009) 1289-1319.

[21] I. Terasaki et al.: Physica B (in press).

寺崎　一郎　TERASAKI Ichiro

早稲田大学　先進理工学部

〒169-8555　東京都新宿区大久保3-4-1

TEL：03-5286-3854　FAX：03-5286-3854

e-mail : terra@waseda.jp

野上　由夫　NOGAMI Yoshio

岡山大学大学院　自然科学研究科

〒700-8530　岡山市北区津島中3-1-1

TEL： 086-251-7770　FAX：086-251-7830

e-mail : nogami@psun.phys.okayama-u.ac.jp