Volume 19, No.2 Pages 91 - 95

1. 最近の研究から／FROM LATEST RESEARCH

スピン・軌道別磁化曲線測定手法の開発
Direct Measurement of Spin and Orbital Magnetization Curve

伊藤　真義　ITOU Masayoshi^[1]、櫻井　吉晴　SAKURAI Yoshiharu^[1]、小泉　昭久　KOIZUMI Akihisa^[2]

^[1]（公財）高輝度光科学研究センター　利用研究促進部門　Research & Utilization Division, JASRI、^[2]兵庫県立大学大学院　物質理学研究科　Graduate School of Material Science, University of Hyogo

Abstract: 　X線磁気コンプトン散乱強度がスピンモーメントに依存するという特徴を利用して、スピン磁気モーメントのみの磁気ヒステリシス直接測定法を確立した。通常の全磁化曲線を参照することにより軌道モーメントのみのヒステリシス曲線の取得も可能である。測定例として、SmAl₂のスピン・軌道別の磁気ヒステリシス曲線、温度依存スピン磁化曲線を取得した。従来の磁気コンプトン散乱において必要であった反転した磁場下での散乱強度の差分ではなく、各点の散乱強度から直接スピン磁気モーメント値を取得しているため、初磁化曲線や、交換磁気異方性などにより磁気ヒステリシスが非対称となる磁化過程も測定が可能となった^[1][1] M. Itou, A. Koizumi and Y. Sakurai: Appl. Phys. Lett. 102 (2013) 082403.。

Download PDF (1.47 MB)

1. はじめに
　磁性研究において磁場依存の磁化測定は最も基本的な実験手法であり、磁化測定手法は超伝導量子干渉磁束計（SQUID）や振動試料型磁力計（VSM：Vibrating Sample Magnetometer）など多くの手法がある。その手法のほとんどは全磁気モーメントを測定するものであり、磁気モーメントをスピン・軌道に分離し計測する実験手法は非常に限られている。X線磁気円二色性測定（XMCD）は数少ないスピン・軌道磁気モーメント分離測定手法である。磁気光学総和則を適応することによりスピン・軌道磁気モーメントの分離を可能とし、元素選択性を有し、表面の磁性に極めて高感度など有用な手段である。
　ここで紹介する手法では、X線磁気コンプトン散乱^[2-4][2] N. Sakai: J. Appl. Cryst. 29 (1996) 81-99.
[3] N. Sakai: "X-Ray Compton Scattering" (OXford University Press, New York, 2004) Chap.10, pp.289-332.
[4] P. M. Platzma and N. Tzoar: Phys. Rev. B 2 (1970) 3556-3559.を利用する。X線磁気コンプトン散乱は、スピン磁気モーメントのみを観測できる手法である。高エネルギーX線を使用するためバルク敏感であり、また測定環境を選ばないなどの特徴をもつ。これまで、X線磁気コンプトン散乱実験は、散乱X線エネルギープロファイルがスピン偏極した電子の運動量密度分布の情報をもつことを利用し、磁性電子の軌道属性の研究やその電子状態の研究などに用いられてきた。一方、その積分強度がスピン磁気モーメントの値に比例することは当初から知られていたが、実験報告は数例しかなく、またその報告も、磁気飽和状態のみや限られた数磁場点のみの測定であった。最近、安居院氏らは磁気コンプトン散乱測定を用いて、Tb₄₃Co₅₇薄膜のスピン磁気モーメントヒステリシス曲線を測定し、また軌道磁気モーメントの分離に成功している^[5,6][5] A. Agui, H. Sakurai, T. Tamura, T. Kurachi, M. Tanaka, H. Adachi and H. Kawata: J. Synchrotron Rad. 17 (2010) 321-324.
[6] A. Agui, S. Matsumoto, H. Sakurai, N. Tsuji, S. Honma, Y. Sakurai and M. Itou: Appl. Phys. Express 4 (2011) 083002.。この報告では、磁化曲線が原点に対し点対称であることを前提として、外部磁化を周期的に変化させ各点で測定を行い、磁化曲線で原点に対し対称な2測定点の差分からスピン磁気モーメントの値を算出している。差分を取らざるをえなかったのは、その散乱断面積の変化の小ささゆえ測定に数日の積算を行うことを強いられたためであり、統計精度の不足と測定装置の時間変動による誤差を、強度の差分を取ることにより緩和させるためである。
　今回紹介する手法では、コンプトン散乱強度変化から直接スピンモーメントを取得する。X線コンプトン散乱強度の変化からスピン磁気モーメントを測定するという原理は過去の報告と同じであるが、光源及び測定器系の信頼性を向上させることにより高精度な測定を実現した。実証として、SmAl₂の磁気のスピン磁気ヒステリシス曲線を測定し、また、それをVSMによる全磁化曲線と照らし合わせることにより軌道磁気ヒステリシスカーブをも取得した。また、同様に温度－スピン磁気モーメント曲線の取得も行った。

2. 散乱断面積
　コンプトン散乱断面積は、電荷散乱項、磁気散乱項に分割して記述できる。

　

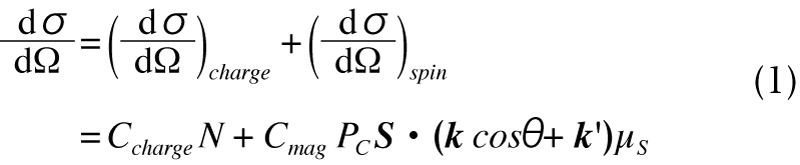
ここで、P_C は入射X線の円偏光度、S は電子スピンの方向ベクトル、k、k’は入射、散乱X線の波数ベクトル、θは散乱角であり、C_charge、C_magは、入射X線エネルギーなどによって決まる定数である。それぞれの項は、第1項が通常の電荷によるコンプトン散乱項であり、これはユニットセル中の全電子数(N)に比例する。第2項は、磁気散乱項（MCS : Magnetic Compton Scattering）であり、スピン磁気モーメント(μ_spi_n)を磁場方向に射影した成分(μ_S)に比例する。磁気散乱項は電子スピンの方向のみが関連し軌道モーメントの寄与はない^[3][3] N. Sakai: "X-Ray Compton Scattering" (OXford University Press, New York, 2004) Chap.10, pp.289-332.ため、コンプトン散乱の電荷散乱に対する強度変化率はスピン磁気モーメントの値に比例する。この変化率（R：磁気エフェクトとも呼ばれる）を、測定点における散乱強度をI と磁化されていない電荷散乱のみの散乱強度をI_nonを用いて式（2）の通りに定義する。

　

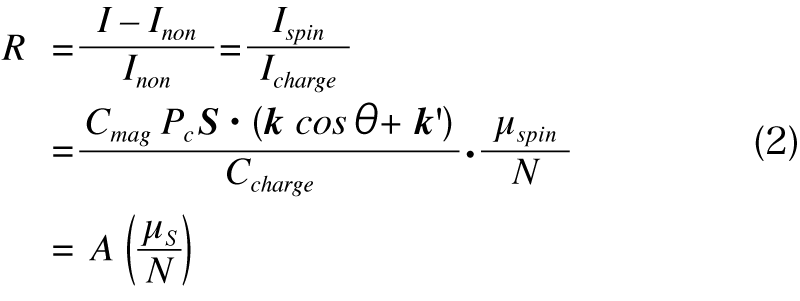
Aは入射X線のエネルギー、円偏光度、散乱角によって決まる定数であるので、測定試料の全電子数（言い換えれば組成）がわかれば、スピン磁気モーメントの値は、散乱強度から直接求めることができる。係数Aは、P_Cという実験パラメータを含んでいるので、同一測定条件においてFeやGdのような磁気スピンモーメントが既知の試料の測定を行うことにより実験的に求めることが多い。

3. 実験装置　条件
　実験は、円偏光成分をもつ高エネルギー高強度のX線を磁場中の試料に照射し、散乱X線強度をある固定した散乱角に設置した検出器で観測する。実験は高エネルギー非弾性散乱ビームラインBL08Wにおいて行った。このビームラインの光源は楕円偏光ウィグラーであり、円偏光成分をもつ100 keV以上の高エネルギーX線を利用することができる。実験はX線エネルギー182.6 keV、円偏光度はP_C～0.55、フラックスはおよそ10¹¹ photons／secの入射X線を使用した。試料からの散乱X線は、散乱角178˚に設置した多素子ゲルマニウム検出器で計測し、検出器出力はマルチチャンネルアナライザで積算した。試料は超伝導マグネット内に設置し、試料への外部磁場の印加方向は入射X線と平行である（図1）。

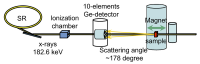
図1. 磁気コンプトン散乱実験装置外観

　測定自体は、試料に外部磁場をかけ、X線散乱強度を測定するという非常に単純なものである。しかし、磁気コンプトン散乱の割合は全コンプトン散乱断面積のたかだか1%程度しかないため、磁気コンプトン散乱強度の変化率を2桁の精度で計測するには、入射X線、散乱X線強度それぞれの強度測定に4桁以上の精度が必要となる。コンプトン散乱X線の強度測定は、コンプトン散乱断面積が小さいためゲルマニウム検出器などでパルス測定を行うのであるが、4桁の統計精度を得るためには8桁のイベントを検出しなくてはならない。そのため、1点の測定に分単位以上時間がかかり、ヒステリシスループを描かせるとなると数時間～数日の測定時間が必要となる。このような長時間測定では、入射X線光学系や測定装置系の長時間安定性が不可欠である。光学機器、装置配置、測定制御システムなどの地味な改良・最適化を積み重ね、装置の安定化を向上させることにより、現在の測定精度は、統計誤差の20%程度となり、また、コンプトン散乱X線／バックグラウンドX線強度比も試料の組成にもよるが1000程度となっている。
　本装置の測定精度を検証するため、アルミニウムのコンプトン散乱強度の磁場依存性を測定した結果が図2(a)である。アルミニウムは常磁性でありこの実験条件では磁化されないため、強度変化は観測されずフラットな形状となる。この測定値の分散が、本計測装置の測定精度に相当する。1点あたり240秒（1回10秒／点の測定を、24周繰り返し積算した）、検出した総散乱光子数は8×10⁷ counts／点、全測定時間2.5時間の測定時間において、測定値の標準偏差は、0.025%であった。この値は、純鉄試料の測定において0.025 μ_B、ガドリニウムにおいて0.07 μ_Bに相当する。もちろん、誤差の主要因は散乱X線測定の統計誤差であるため、測定時間を長くすることにより高精度の測定が可能である。

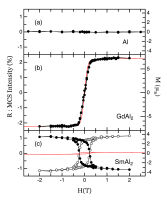
図2. (a)Al、(b)GdAl₂、(c)SmAl₂の磁場依存磁気コンプトン散乱(MCS)強度（黒丸）、及び、VMSによるヒステリシス曲線（赤実線）。MCS強度は、GdAl₂測定からスピン磁気モーメントに校正されている。(c)における白丸は（全磁気モーメント）－（スピン磁気モーメント）を示し、軌道磁気モーメントに対応する。

4. 測定例
　測定の実行可能性を示すために、GdAl₂単結晶のヒステリシス測定を行った。GdAl₂は強磁性体であり、その磁気異方性は非常に小さく^[7][7] E. M. Levin, V. K. Pecharsky and K. A. Gschneider: J. Appl. Phys. 90 (2001) 6255-6262.、軌道磁気モーメントはほぼ消失しており全磁気モーメント＝スピン磁気モーメントと考えてよいため、本手法の実証に適していよう。図2(b)に、コンプトン散乱X線強度の磁場依存性（黒丸）と、VSMによる全磁気モーメントの磁化曲線（赤実線）を示す。試料はコンプトン散乱測定、VSM測定ともに同じものを使用し、試料温度は5 Kである。MCS測定では、外部磁場+2 Tから-2 Tを往復する全83磁場点においてコンプトン散乱強度を測定した。1点あたり420秒（10秒／点、42周）、検出した総コンプトン散乱光子数は2.6×10⁷ counts／点、全測定時間は14時間であった。単位時間あたりの散乱X線計測数がAlの測定に較べ小さいのは、Gdの光電吸収断面積の大きさゆえである。コンプトン散乱X線MCSの強度変化は、ゼロ磁場におけるコンプトン散乱強度をゼロとして百分率（%）で表している。また、左右の縦軸に示したMCS強度と磁気モーメントは、飽和磁場下において一致するようにスケーリングして表示している。図からわかるように、コンプトン散乱X線は、外部磁場の変化に伴いその強度が明確に変化していることが確認でき、試料の磁化情報を取得できていることがわかる。また、その強度変化曲線の形状は、VSMによる磁化曲線と非常によい一致をしている。先に述べたようにGdAl₂では全磁化はスピン磁化のみと考えてよい。スピンモーメントの絶対値を算出するには、式(2)に示すとおり、全コンプトン散乱強度の変化から導き出すが、ここでは、このGdAl₂の測定から定数Aを求め、以降のSmAl₂測定に適応することにする。散乱強度を求める際、実際には、バックグラウンドX線や、試料内の多重散乱などを検証し除去しなくてはならない。これらの値は実験的に、もしくは計算によって求めることもできるが、今回のGdAl₂、SmAl₂の測定では試料組成、形状が似ておりバックグラウンド・多数散乱もほぼ同一と考えてよく、これらを含んだ定数Aを使用した。
　次に、SmAl₂の測定を示す。Smは4 f電子数が6個（less than half）であり軌道モーメントとスピンは逆向きとなる。VSM測定、MCS測定とも同じ試料を使用し、試料温度は、VSMは5 K、MCSでは10 Kで行った。MCS測定条件は、測定点は全59磁場点、1点あたり320秒（10秒／点、32周）、検出した総コンプトン散乱光子数は2.0×10⁷ counts／点、全測定時間は8時間であった。図2(c) に測定結果を示す。図中、赤実線はVSMによる全磁気モーメント、黒丸はMCS強度変化でスピン磁気モーメントに対応する値であり、白丸は全磁気モーメントとスピン磁気モーメントの差分、すなわち軌道磁気モーメントに相当する。MCSにおける磁気モーメント値は、GdAl₂の測定で得た校正値を用いて換算した。ほぼ飽和した状態である2 Tにおいて、全磁気モーメントは0.2 μ_Bとそれほど大きくはないが、磁気コンプトン散乱で得たスピン磁気モーメントは-3.5 μ_Bであり、全磁気モーメントに対し非常に大きな値を示した。また、GdAl₂の結果と対称的にMCSの強度変化はVSMのシグナルと逆符号方向へと変化している。これはSmAl₂のもつ磁気モーメントは、軌道磁気モーメントが優勢であり、スピンモーメントは軌道磁気モーメントと逆向きに結合しておりほぼ打ち消し合っていることを示す。全磁気モーメント、スピン磁気モーメントから得られた軌道磁気モーメントは3.7 μ_Bとなる。これらの値は、安達氏らによる報告^[8][8] H. Adachi, H. Ino and H. Miwa: Phys. Rev B 59 (1999) 11445-11449.とよい一致を示していた。さらに、スピン磁気モーメントの磁気ヒステリシスと軌道磁気モーメントの磁気ヒステリシス曲線は、逆符号でほぼ同様な形状の磁気ヒステリシスが観測され、保持力は一致することが初めて確認された。
　MCSでは、上記のような磁場依存性の測定だけではなく温度依存性の測定も可能である。外部磁場依存の磁化曲線測定と同様に、温度依存測定も当然ながら可能である。図3は、外部磁場2.5 TにおけるSmAl₂においてMCS強度の温度依存を測定した結果である。測定は、降温、昇温双方において行い、各点での測定時間は240秒／点、全測定時間は7時間であった。この測定では、外部磁場を±2.5 Tとし、入射X線と平行、及び反平行に印加してその差分を取っている。図3からわかるように、MCS強度は、温度低下に伴い、約100 Kで減少を開始し、また、温度上昇においてもほぼ同じ曲線上を戻った。この結果は、本手法の実効性を示すものであろう。一方、この測定での転移点は約100 Kであり、文献［8］の報告値125 Kから低い値を示した。この理由は解明できていないが、転移点付近でスピン軌道相互作用に何らかの変化が起こっていることをうかがわせる。

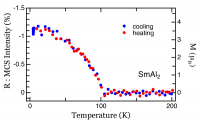
図3. SmAl₂の温度依存磁気コンプトン散乱強度曲線

　ここまでの測定では、コンプトン散乱X線強度のみを対象として、測定結果を示してきた。一方で、いままでの多くの磁気コンプトン散乱研究実験で示されているように、コンプトン散乱X線プロファイルは、電子運動量密度分布の情報をあたえるものである。この情報を利用すれば、スピン磁気モーメント値のみでなく、スピン磁化モーメント曲線の軌道選別測定の可能性がある。

5. まとめ
　磁化測定法にX線磁気コンプトン散乱法を組み合わせ、スピン磁気モーメントの磁気ヒステリシスと軌道磁気モーメントの磁気ヒステリシスを分離して、高精度に測定する手法の開発に成功した。SmAl₂での実証測定の結果は、2 Tにおいて全磁気モーメント0.2 μ_B、スピン磁気モーメント-3.5 μ_B、軌道磁気モーメントは3.7 μ_Bであり、これらは先行研究値と一致した。スピン磁気モーメントの磁気ヒステリシスと軌道磁気モーメントの磁気ヒステリシス曲線は、磁化の符号の反転したほぼ同様な磁気ヒステリシスが観測され、保持力は一致することが初めて確認された。
　本測定手法は、散乱X線強度からスピン磁気ヒステリシスを直接かつ高精度に導出するものであり、従来のコンプトン散乱測定では困難であった初磁化過程や、交換スプリング結合、交換磁気異方性などにより磁気ヒステリシスが非対称となる磁化過程も測定可能である。また、バルク敏感な測定であり、試料環境を選ばないことから、他の一般的な磁化測定法やMCDと相補的な知見を得ることができよう。磁性の発現機構の解明や、スピントロニクスデバイス、永久磁石材料の設計・性能評価に有用なツールとして期待される。また、さらに高輝度な100 keVオーバーの光源や、それに対応した移相子が実用化されれば、さらに高精度で、磁性電子の軌道選別測定や運動量密度変化に着目した実験も可能になるであろう。

謝辞
　VSMによる磁化曲線取得には岡山大学の神戸高志准教授のご協力をいただいた。厚くお礼を申し上げる。磁気コンプトン散乱測定は、大型放射光施設SPring-8（課題番号2007A1262、2010A1923）での成果である。

参考文献
[1] M. Itou, A. Koizumi and Y. Sakurai: Appl. Phys. Lett. 102 (2013) 082403.
[2] N. Sakai: J. Appl. Cryst. 29 (1996) 81-99.
[3] N. Sakai: "X-Ray Compton Scattering" (OXford University Press, New York, 2004) Chap.10, pp.289-332.
[4] P. M. Platzma and N. Tzoar: Phys. Rev. B 2 (1970) 3556-3559.
[5] A. Agui, H. Sakurai, T. Tamura, T. Kurachi, M. Tanaka, H. Adachi and H. Kawata: J. Synchrotron Rad. 17 (2010) 321-324.
[6] A. Agui, S. Matsumoto, H. Sakurai, N. Tsuji, S. Honma, Y. Sakurai and M. Itou: Appl. Phys. Express 4 (2011) 083002.
[7] E. M. Levin, V. K. Pecharsky and K. A. Gschneider: J. Appl. Phys. 90 (2001) 6255-6262.
[8] H. Adachi, H. Ino and H. Miwa: Phys. Rev B 59 (1999) 11445-11449.