Volume 12, No.2 Pages 180- 188

1．はじめに
　タイトルを見て「これは自分の専門と縁遠いな」とページを飛ばそうとしている読者の方、もう少しお読みいただきたい。今回私達は研究報告を、様々な科学的バックグラウンドを持った読者が対象であるSPring-8利用者情報に執筆するにあたり、物性物理以外を専門とする方々にも分かりやすく理解できるよう記したつもりである。本稿でSPring-8における軟X線利用実験の一つである角度分解光電子分光の目的や利点をつかんでいただければ幸いである。なお専門家から見ると一部厳密でない表現があるかもしれないがご容赦いただきたい。
　私達が研究対象とする結晶固体（主に金属）の電気的・磁気的性質（なぜ電流を流しやすいか、何故磁石にくっついたりするか等）は主に固体中の電子のなかで最もエネルギーが高い電子（価電子・伝導電子）の振る舞いに支配される。よって固体の電子状態を詳しく調べることは、その固体の性質を理解する上で重要であるが、さらにその固体が例えば超伝導や金属−絶縁体転移、磁性転移といった興味深い現象をみせる場合にはそれらの起源を理解する上でも同様に重要である。本稿では本研究で用いた軟X線角度分解光電子分光（ARPES）で、固体内部の電子状態を正に直接的かつ3次元的に調べる事ができること、そして今回の測定例^［1］[1] M. Yano, A. Sekiyama, H. Fujiwara, T. Saita, S. Imada, T. Muro, Y. Onuki and S. Suga : Phys. Rev. Lett. 98 (2007) 036405.まで以下順を追って丁寧に説明する。


2．金属固体の電子構造
　ここから主に金属を念頭において説明する。金属固体中の一部の電子は固体中を自由に動き回れると考えて物理を展開するとその性質を良く説明できる事が多い。はじめにその状況を極限までもっていって「ある空間の中に閉じ込められて、その中を他の電子の影響をうけることなく自由に動けるN個の電子で構成される」自由電子気体を考える。電子は中でバラバラに動き回っているので一見するとうまく記述できないように思うかも知れないが、電子の運動量p（古典物理では電子質量m、速度vとしてmvとなる）に着目すると量子力学の法則から自由電子の振る舞いは以下のような規則に従う^［2］[2] 量子力学の啓蒙書としては、例えば並木美喜雄「量子力学入門(」岩波新書・新赤版、1992)など。。簡単の為長さLの直線上しか動けない1次元自由電子をみると、運動量はプランク定数hとしてh/Lの単位で量子化される、つまり運動量が連続的でなく離散的になる。また「2つ以上の粒子は全く同じ状態になることができない」というパウリの排他律と、N個の電子全体としてエネルギーを最小にしようとする熱力学の法則及び1個の電子のエネルギーεが（1/2）mv²=p²/（2m）と運動量に応じて大きくなることから2n-1、2n個目の電子の運動量は±nh/Lとなる（正負の異なる同じ大きさの運動量がある為。ここではスピンの存在を無視している）。最もエネルギーの高い電子は大きさNh/（2L）の運動量を持ち、そのエネルギーをフェルミ準位E_Fと表す。この様子を運動量成分p_x, p_y, p_zを座標軸にとった運動量空間で表すとフェルミ準位の電子は図1のようにp_x=±Nh/（2L）で表される平面上に存在することになり、この面をフェルミ面と呼ぶ。フェルミ面形状は面積Sの2次元平面中の自由電子気体の場合はε=（p_x²+p_y²）/（2m）となることからp_x²+p_y²=Nh²/（πS）で表される円筒状に、体積Vの等方的3次元空間中の自由電子気体ならp_x²+p_y²+p_z²=h²｛3N/（4π²V）｝^2/3で表される球状になる。N個の電子全体としての運動量、つまり個々の電子運動量の総和は0である為、全体でみると並進運動はしておらず電流は流れない。このような自由電子気体に"電流"を流す為には"両端"に電圧をかけ、電子が電場を感じて運動量変化し、運動量総和が0からずれる必要がある。このずれた状態を元の状態と運動量空間上で全体的に比べると、2次元の場合のみ図2に示したが、フェルミ面及びそのごく近傍の状態にある電子だけが運動量変化を起こしている事がわかる。つまり電気伝導を担う伝導電子はフェルミ面とその近傍に対応する運動量を持つ電子だけとみなせる。実際の物質でも事情は似ており、フェルミ面＝伝導電子の運動量分布を実験的に知る事の重要性の理由の一つがここにある。



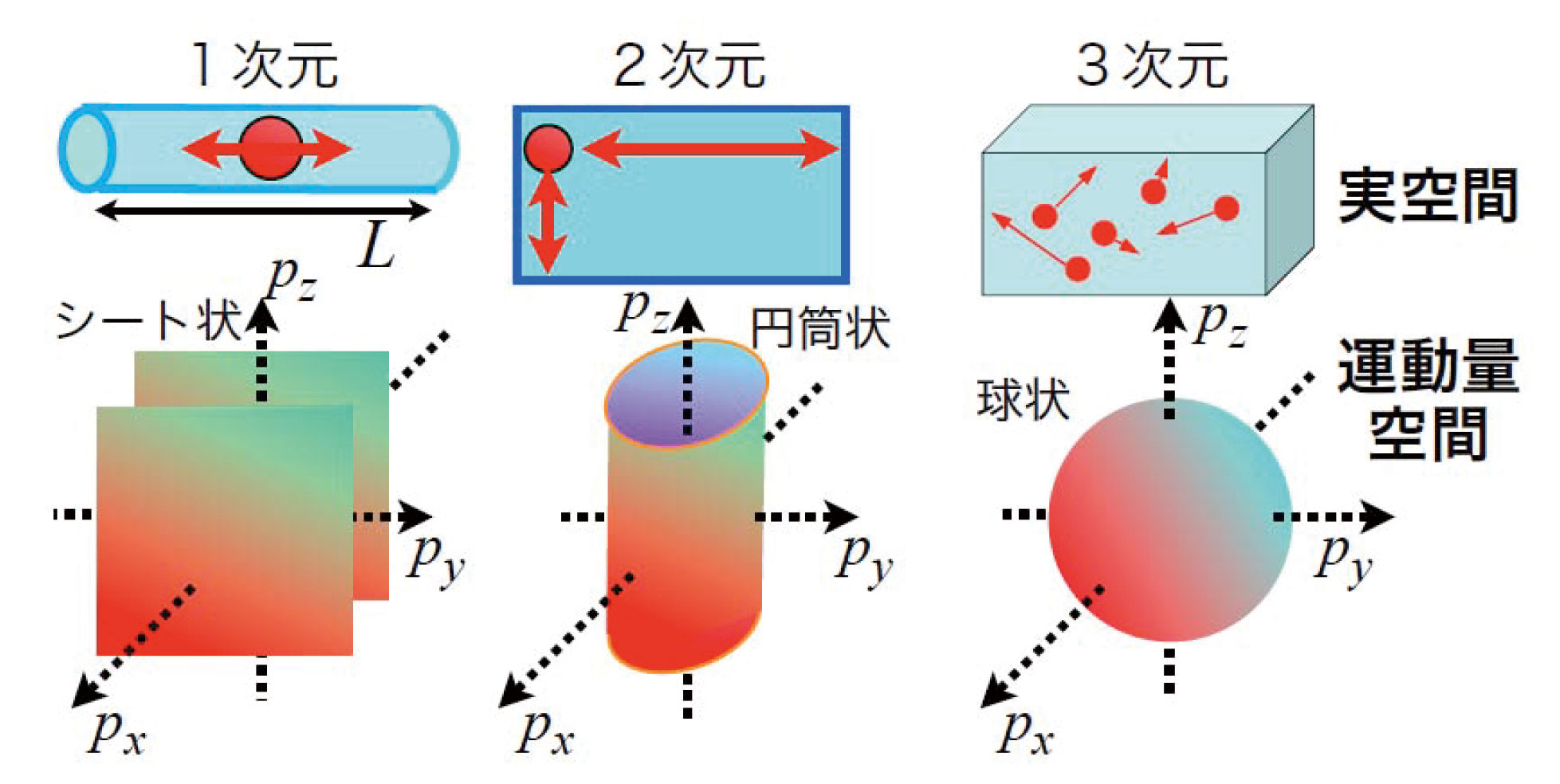
図1　1次元、2次元及び3次元空間内の自由電子気体が作るフェルミ面（最もエネルギーの高い電子の運動量分布）。




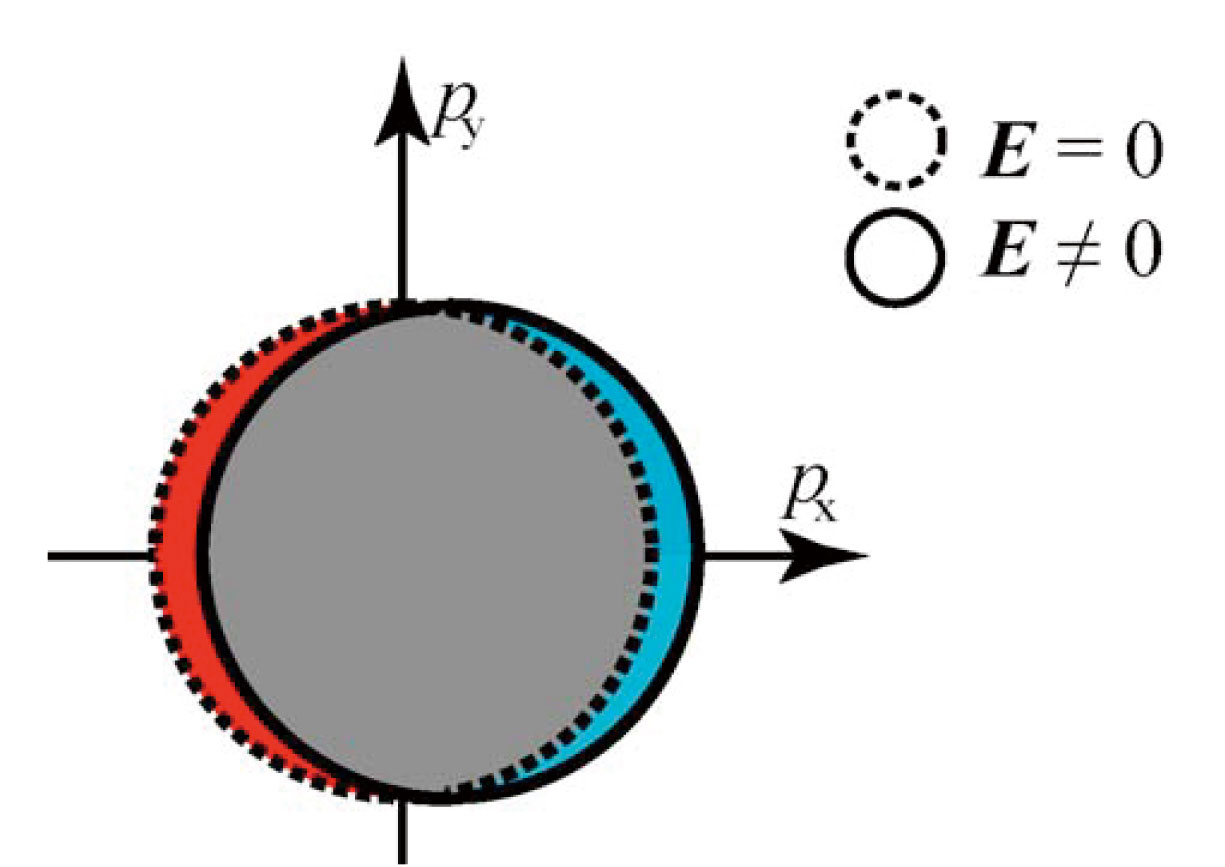
図2　2次元自由電子気体について、電場をかけた時（E≠0）のフェルミ面（実線の円）と電場をかけない時（E＝0）のフェルミ面（破線）の比較。電場をかけることで青い（赤い）領域の運動量を持つ電子が新たに出現（消滅）する。いずれの領域もフェルミ面近傍の電子の変化であり、それらの電子だけが電場に敏感に反応しているとも言える。


　実際の物質では勿論上記のように単純ではないが、運動量が（準位間の差が限りなく小さいとしても）離散準位化する事やパウリの排他律が成り立つ事は変わらず、主に以下の4つの事情を追加して考えればよい。（1）空間的に規則正しく配置された原子核が作る周期的ポテンシャルエネルギーのため電子状態は位置的にも運動量の関数としても周期性をもつ。（2）自由に動けるかにみえる伝導電子が実際は特定の原子核に強く束縛されているかのような状態もとり得る。（3）電子のスピンの存在及び電子の磁気モーメント（小さい磁石としての役割）が固体の、特に磁気的性質に大きな影響を与える。（4）電子同士のクーロン斥力に起因する電子相関や電子が原子核振動の影響を受ける電子格子相互作用が固体の性質に影響を与え得る。（1）については図3のように原子核が間隔aで並んだ1次元鎖中の電子状態を例にとると、電子からみてある原子核からa+xだけ離れた状態は、隣の原子核からxだけ離れた状態と何ら区別がつかないため同じ状態のはずである。これは電子状態が空間的にaの周期性を持っている事を意味する。このような状況の電子に量子力学を適用すると電子状態は運動量に対しても、結果としてh/aの周期性を持つ事が知られている（ブロッホの定理）^［3］[3] ブロッホの定理については、キッテル「固体物 理学入門」(丸善)やザイマン「固体物性論の 基礎」(丸善)など固体物理/物性物理の教科書を見ていただきたい。。よって電子状態を記述する際には±h/（2a）の範囲の運動量について考えればあとは周期的に同様の状態が運動量空間内に出てくる。このような周期性は３次元物質でも同様に適用でき、電子状態は運動量空間内で"立体的"な周期性を持つ。この時の（1次元の時の±h/（2a）の範囲に対応する）最小周期性の単位をもつ運動量範囲をブリルアン域と呼ぶが、これは結晶構造で決定される。このブリルアン域に対応した周期性は運動量分布であるフェルミ面にも影響を与える。図4に示すように先に紹介した自由電子気体のフェルミ面がブリルアン域より大きいと、周期性を満たす為に境界で折り返し変形を受ける。後で紹介するCeRu₂Ge₂の簡略化した結晶構造と対応するブリルアン域は図5のようになる^［4］[4] M. J.Besnus, A. Essaihi, N. Hamdaoui, G. Fischer, J. P. Kappler, A. Meyer, J. Pierre, P. Haen and P. Lejay : Physica 171B (1991) 350-352.。（2）については前述の自由電子に対するエネルギーと運動量の関係（分散関係）が成り立たなくなる事を意味する。現実の物質に対する分散関係はバンド計算で予測可能だが、実験的には本稿の角度分解光電子分光が殆ど唯一の探索手法であり、この点でもその重要性が分かる。また、磁気的性質は（2）,（3）の両方の影響を強く受け、特に私達が研究対象とする3d電子系物質、後で紹介する4f電子系物質では重要になってくる。（4）はモット転移・高温超伝導・超巨大磁気抵抗・量子臨界現象・重い電子系や近藤半導体の出現といった面白い現象を示す強相関遷移金属酸化物^［5］[5] テキストとしては例えば津田惟雄、那須奎一郎、藤森淳、白鳥紀一「電気伝導性酸化物(改訂版)」(裳華房物性科学選書、1993)。や希土類化合物^［6］[6] テキストとしては例えば上田和夫、大貫惇睦「重い電子系の物理」(裳華房物理学選書23、 1998)。では必ず顔をだす要素である。つまり物質の電子状態は実際のところは当たり前だが「調べてみないと分からない」のであり、それ故に色々と研究する必要があるのは言うまでもない。



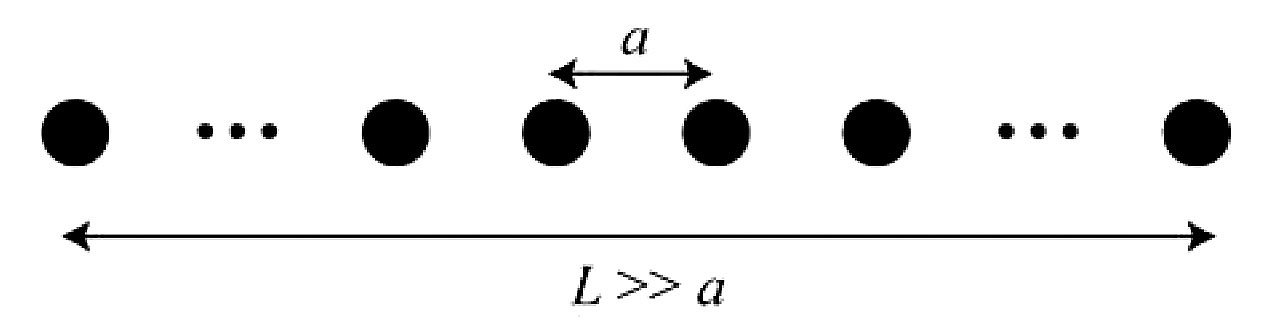
図3　原子核が1次元的に直線上に並んだ系。考える全体の長さLは原子間間隔aよりも十分長い。




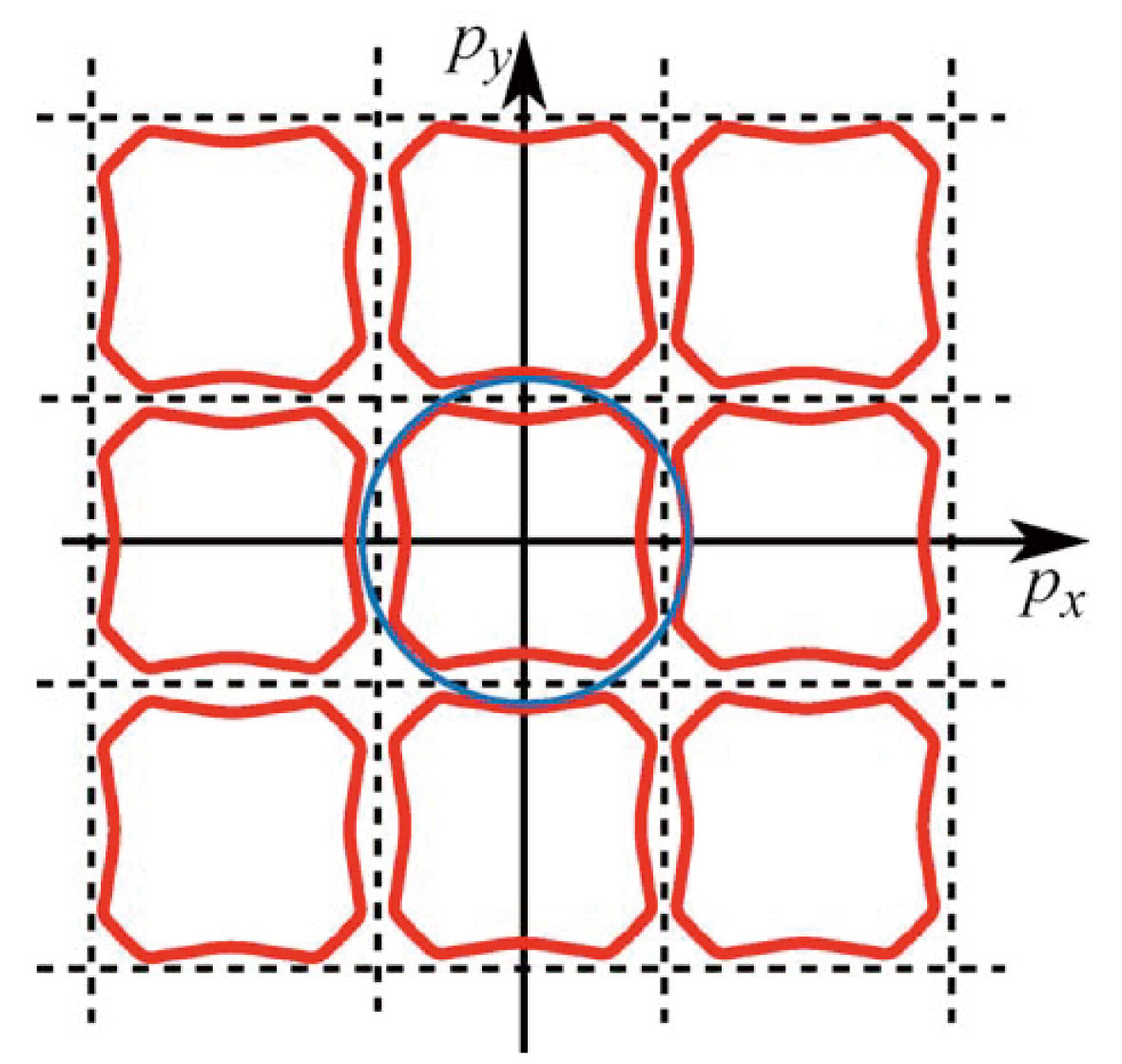
図4　2次元自由電子気体の作るフェルミ面（水色）がブリルアン域の存在によって、破線で示す境界で折り返し変形を受け、周期性を持った状態（赤色）。




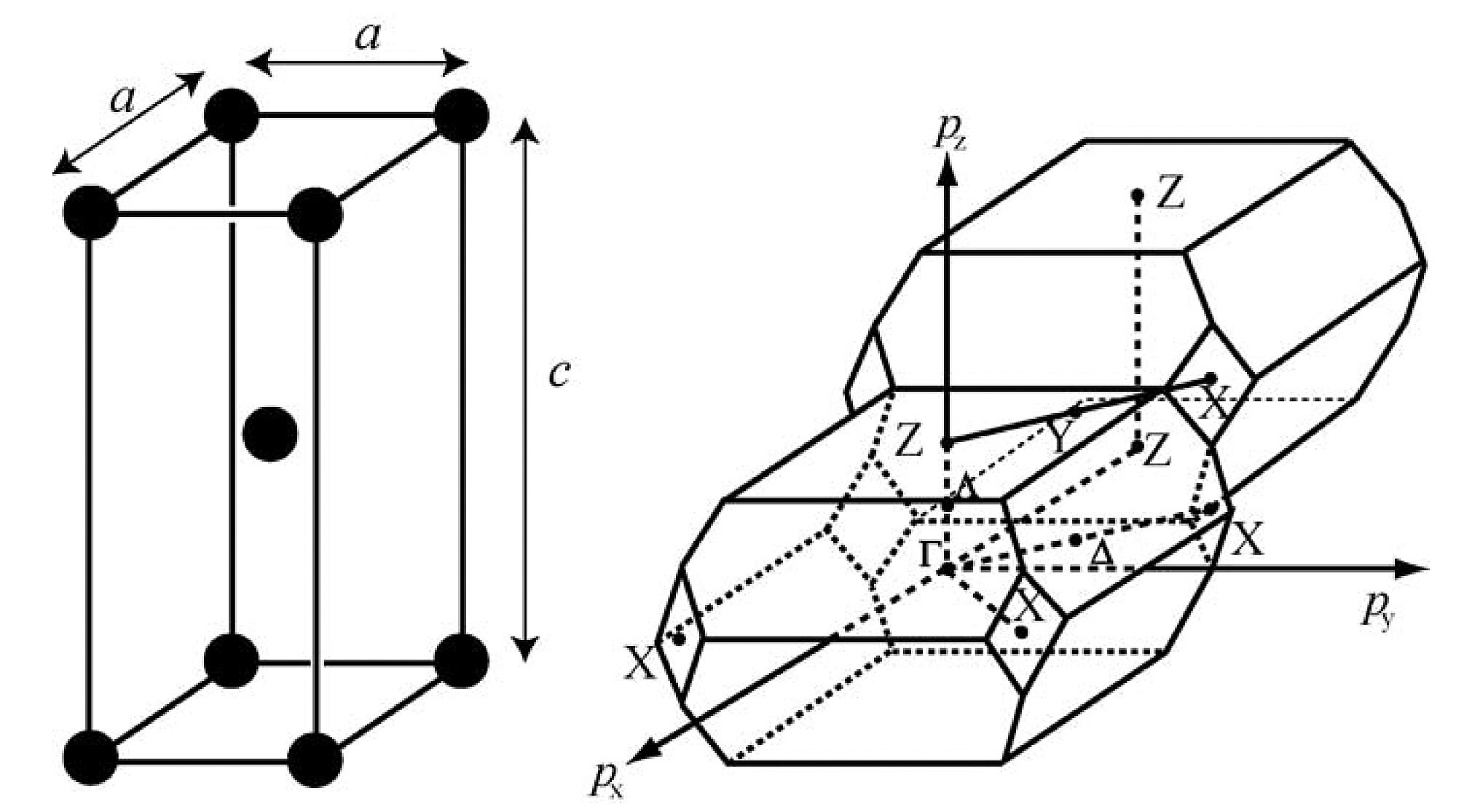
図5　CeRu₂Ge₂の簡略化した結晶構造（体心正方晶、左）と対応するブリルアン域（右）。左図の黒丸はCeイオンを示す。Γ, Z, Xは運動量空間内の点を示し、対応する座標はそれぞれ（0,0,0）,（0,0,h/c）,（h/（2a）,h/（2a）,0）。なお周期性から上記座標に3つのベクトル（h/a,0,-h/c）,（0,h/a,-h/c）,（0,0,2h/c）もしくはその任意の線形結合によるベクトルを足し引きして出てきた座標も等価になる。例えば（0,0,0）の他に（±h/a,0,±h/c）,（0,±h/a,,±h/c）等もΓ点であり、（0,0,h/c）の他に（±h/a,0,0）,（0,±h/a,0）,（±h/a,0,3h/c）等もZ点である（復号任意）。


3．SPring-8における軟X線角度分解光電子分光による電子構造研究
　電子構造、特にフェルミ面を実験的に調べる手法としては、物質に強い磁場をかけて生じる磁気抵抗の振動を測定してフェルミ面の極値断面積を知る量子振動測定［例えばドハース・ファンアルフェン（dHvA）効果］が古くから知られている。この手法は単純金属や強相関希土類化合物で威力を発揮する一方で、不純物の極めて少ない単結晶を通常数K以下の低温下で測定する事が通常要求される。よって温度変化で相転移を起こす物質の"高温"でのフェルミ面を調べるのは多くの場合難しい。これを克服する他の実験手法としては角度分解光電子分光（ARPES、図6）がある。光電子分光ではエネルギーhvの単色光を物質に当て、エネルギー保存則E_B=hv−E_K（E_B：励起前の電子の結合エネルギー、E_K：光電子運動エネルギー、物質の仕事関数の項は簡単の為省略）によりE_Kを観測することで電子の結合エネルギーを知る。観測する光電子放出角を限定するARPESは（詳細は後述するが）電子の運動量とエネルギーの関係（バンド分散）を直接観測できる。様々な角度に対して測定することでフェルミ準位上の電子の運動量分布、すなわちフェルミ面を直接観測することが可能である。




図6　角度分解光電子分光の概念図


　これまでのARPESでは100eV程度以下の低エネルギー励起で光エネルギーを固定した測定によってフェルミ面を2次元的に調べることがよく行われてきた。近年のエネルギー及び運動量（角度）分解能向上により、擬2次元的な電子構造を持つと考えられている高温超伝導体を含む層状遷移金属酸化物で威力を発揮してきたかにみえる^［7］[7] A. Damascelli, Z. Hussain and Z.-X Shen : Rev. Mod. Phys. 75 (2003) 473-541.。しかし従来の低エネルギー励起では観測する光電子運動エネルギーが低い為、光電子脱出深さλが数Å程度と短く、主に固体表面から出てきた光電子を、つまり固体内部ではなく表面の電子状態を強く観測していた。固体表面は内部と異なる電子状態になる場合が多く、特に私達がよく研究対象として扱う強相関物質では表面と内部の違いは顕著と考えられる。実際私達はこれまで角度積分光電子分光によってそのことを実証してきた^［8-11］[8] A. Sekiyama, T. Iwasaki, K. Matsuda, Y. Saitoh, Y. Onuki and S. Suga : Nature 403 (2000) 396-398.
[9] A. Sekiyama, K. Kadono, K. Matsuda, T. Iwasaki, S. Ueda, S. Imada, S. Suga, R. Settai, H. Azuma, Y. Onuki and Y. Saitoh : J. Phys. Soc. Jpn. 69 (2000) 2771-2774.
[10] A. Sekiyama, S. Suga, S. Ueda, S. Imada, K. Matsuda, T. Iwasaki, M. Hedo, E. Yamamoto, Y. Haga, Y. Onuki, Y. Saitoh, T. Matsushita, T. Nakatani, M. Kotsugi, S. Tanaka and H. Harima : Solid State Commun. 121 (2002) 561-564.
[11] A. Sekiyama, H. Fujiwara, S. Imada, S. Suga, H. Eisaki, S. I. Uchida, K. Takegahara, H. Harima, Y. Saitoh, I. A. Nekrasov, G. Keller, D. E. Kondakov, A. V. Kozhevnikov, Th. Pruschke, K. Held, D. Vollhardt and V. I. Anisimov : Phys. Rev. Lett. 93 (2004) 156402.。また、電子は通常3次元的に動き回るので運動量分布も3次元的に調べる必要があるが、従来の低エネルギー角度分解光電子分光では前述の表面敏感性の問題もありそれが困難であった。
　私達は従来のARPESの欠点を克服する為に高エネルギー軟X線励起によるARPESをこれまで開発し、測定を進めてきた。この手法の利点は
・表面からの信号強度を抑制し、固体内部から出てきた光電子を観測
・フェルミ面を3次元的に可視化（直接観測）することが可能
・低温だけでなく数百Kまでの高温でフェルミ面観測が可能
というところにある。図7のように、光電子の脱出深さλは運動エネルギーE_Kが大きくなると深くなり、500〜1000eVでは物質にもよるが10〜20Åとなるため固体内部から出てきた光電子を観測できる。また図8に示すように光電子は励起前の運動量の情報を持っており、光電子の試料表面に平行な成分は固体内でも真空中に飛び出しても保存され、元の平行成分p_xは光速をcとしてp_x=（2mE_K）^0.5sinθ−（hv/c）sinφの関係式を持ち実験時のE_K、θ（電子放出角）、hv、φ（光の入射角）を代入すれば分かる（厳密には後述のp_cも右辺にかかるが、現実に意識する必要は普段はない）。ARPESの説明では試料表面に垂直な方向（面直方向）について丁寧に説明される事が意外と少ないためか「ARPESでは面直方向のエネルギーと運動量の分散関係が分からない」あるいは「面直方向の運動量は積分される」と思われる事がしばしばあるが、それは高エネルギーARPESに関して言えば誤解である。元の面直方向の運動量成分p_zはp_z=（2mE_Kcos²θ+V₀）^0.5＋（hv/c）cosφ−p_cで与えられる。ここでp_cは前述の運動量空間における周期性を表すブリルアン域に対応した結晶運動量であり測定試料の結晶構造・格子定数とヘキ開面が分かっていれば求まるものである為V₀以外の量は既知であり、励起エネルギーhvを少しずつ変えた実際のARPES測定で分散関係を見ればV₀も決定できる（分散の折り返しが分かれば運動量空間のどこを測定しているかが分かるのでV₀の見積りそれ自身は電子構造研究という点ではあまり重要ではなくなる）。つまり図9のように励起エネルギーを変えながら高エネルギーARPESを行う事で、分散関係とフェルミ面を3次元的に知る事が可能になる。面直運動量p_zの観測によるぼけ（分解能）は脱出深さλの逆数に比例しh/（2πλ）と考えられる^［12］[12] H. Wadati, A. Chikamatsu, M. Takizawa, R. Hashimoto, H. Kumigashira, T. Yoshida, T. Mizokawa, A. Fujimori, M. Oshima, M. Lippmaa, M. Kawasaki and H. Koinuma : Phys. Rev. B 74 (2006) 115114.ので、実は高エネルギーARPESの固体内部敏感性が同時にp_zのよく分解された測定に寄与するのである。逆に表面敏感な低エネルギーARPESではp_zぼけが大きくなるため「面直運動量をある程度積分したものがARPESスペクトルになる」という状況が発生する。また、ARPESは高温でも測定可能であり「高温でのフェルミ面」も観測できる事は、dHvA効果を利用した量子振動測定にはない大きな利点である。私達はこれまでにも擬1次元、擬2次元遷移金属酸化物に対して高エネルギーARPESを行ってきたが、室温でも意味のある測定が可能であることを確かめている^{［13,14,15］}[13] A. Sekiyama, S. Kasai, M. Tsunekawa, Y. Ishida, M. Sing, A. Irizawa, A. Yamasaki, S. Imada, T. Muro, Y. Saitoh, Y. Onuki, T. Kimura, Y. Tokura and S. Suga : Phys. Rev. B 70 (2004) 060506(R).
[14] S. Suga, A. Shigemoto, A. Sekiyama, S. Imada, A Yamasaki, A. Irizawa, S. Kasai, Y. Saitoh, T. Muro, N. Tomita, K. Nasu, H. Eisaki and Y. Ueda : Phys. Rev. B 70 (2004) 155106.
[15] 菅滋正:SPring-8利用者情報 Vol.10, No.3 (2005) 194-199.。




図7　高（低）エネルギー光電子分光の固体内部（表面）敏感性




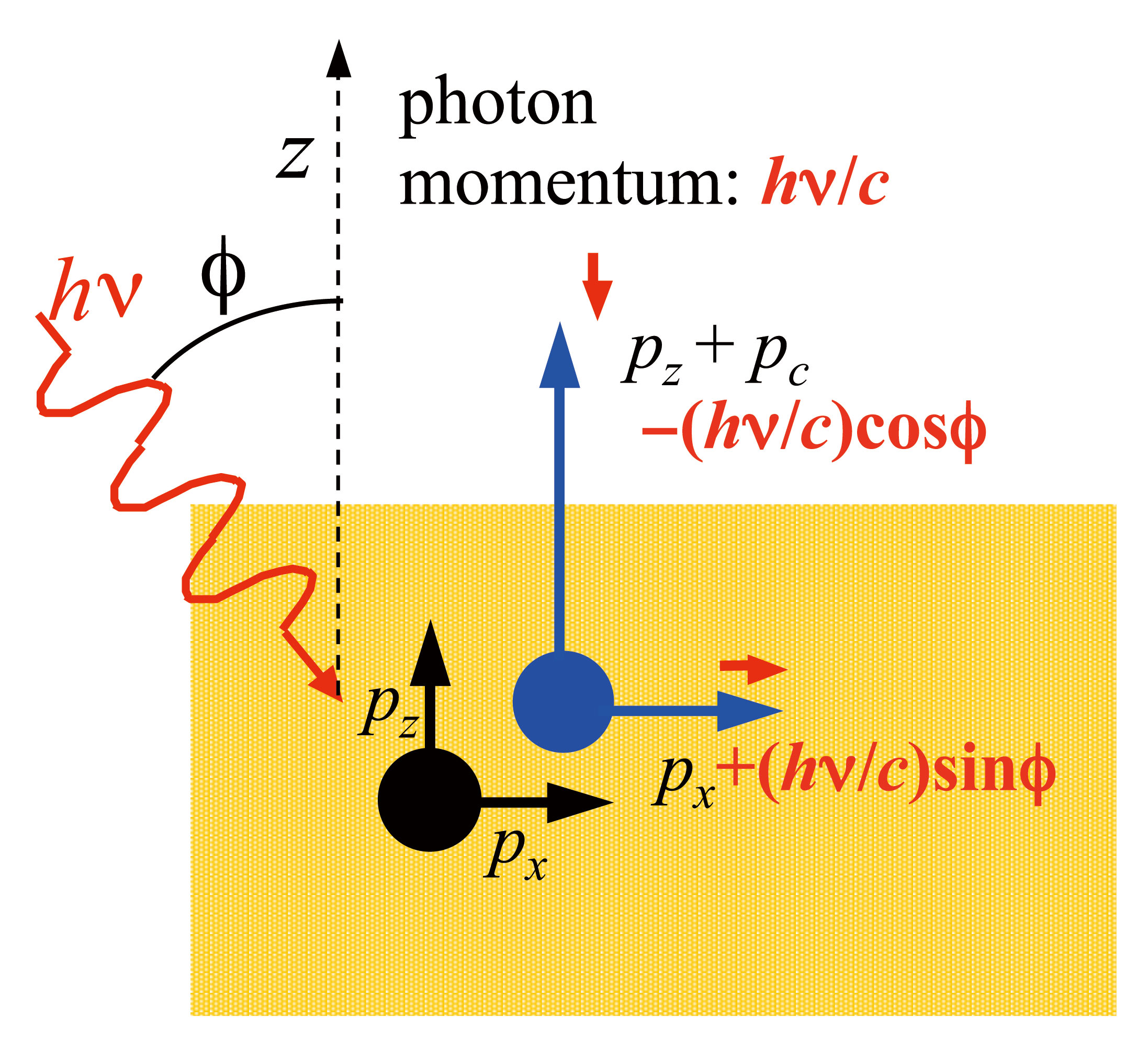
図8　角度分解光電子過程前後の電子運動量（前：黒色、後：青色）。図中のp_cは結晶運動量と呼ばれるものであり、図4のブリルアン域であれば（0,0,2h/c）の定数倍になる。低エネルギー励起ARPESでは光の運動量は電子のそれに比べてはるかに小さいため無視されることが多い。




図9　励起エネルギー依存軟X線角度分解光電子分光による3次元的フェルミ面マッピングの概念図


　私達は高エネルギーARPESをSPring-8 BL25SUで測定している。図10に実際に測定したデータの一例を示す。高エネルギー励起では1回の測定で一方向に対してブリルアン域全体（角度にして±4〜5°程度）をカバーしたARPESスペクトル（ある運動量の電子のエネルギー分布EDC）が80本程度測定できる。図10の強度プロットは正にフェルミ準位E_F（=結合エネルギー0eV）近傍の電子のエネルギーと運動量の分散関係を表したものであり、E_Fでの運動量分布MDCをみることで、どの運動量がフェルミ面上にあるかが実験的に分かる。特定のp_zにおける2次元的なフェルミ面は、hv一定にして角度を変えながらARPES測定すれば可能（図9の赤い運動量平面のスキャンに対応）である。これに加えて角度一定にしてhvを変えながら測定すれば図9の青い運動量平面のスキャンに対応し、フェルミ面を3次元的に調べる事が可能になる。1つの試料に対して色々な角度とhvでの測定が必要になり時間のかかる実験である。また角度積分測定に比べ角度分解測定は当然ながら1本のスペクトル強度は桁落ちに弱い。さらに相対的に光電子強度は高エネルギー励起になるほど弱くなるので明るく、かつエネルギー分解能の高い励起光が必要である。さらにhv変化測定を必要とするのでユーザーが自由にアンジュレータギャップを迅速に制御できなくてはいけない。これらが高エネルギーARPESでBL25SUをはじめとするSPring-8の高輝度軟X線が必要な所以である。




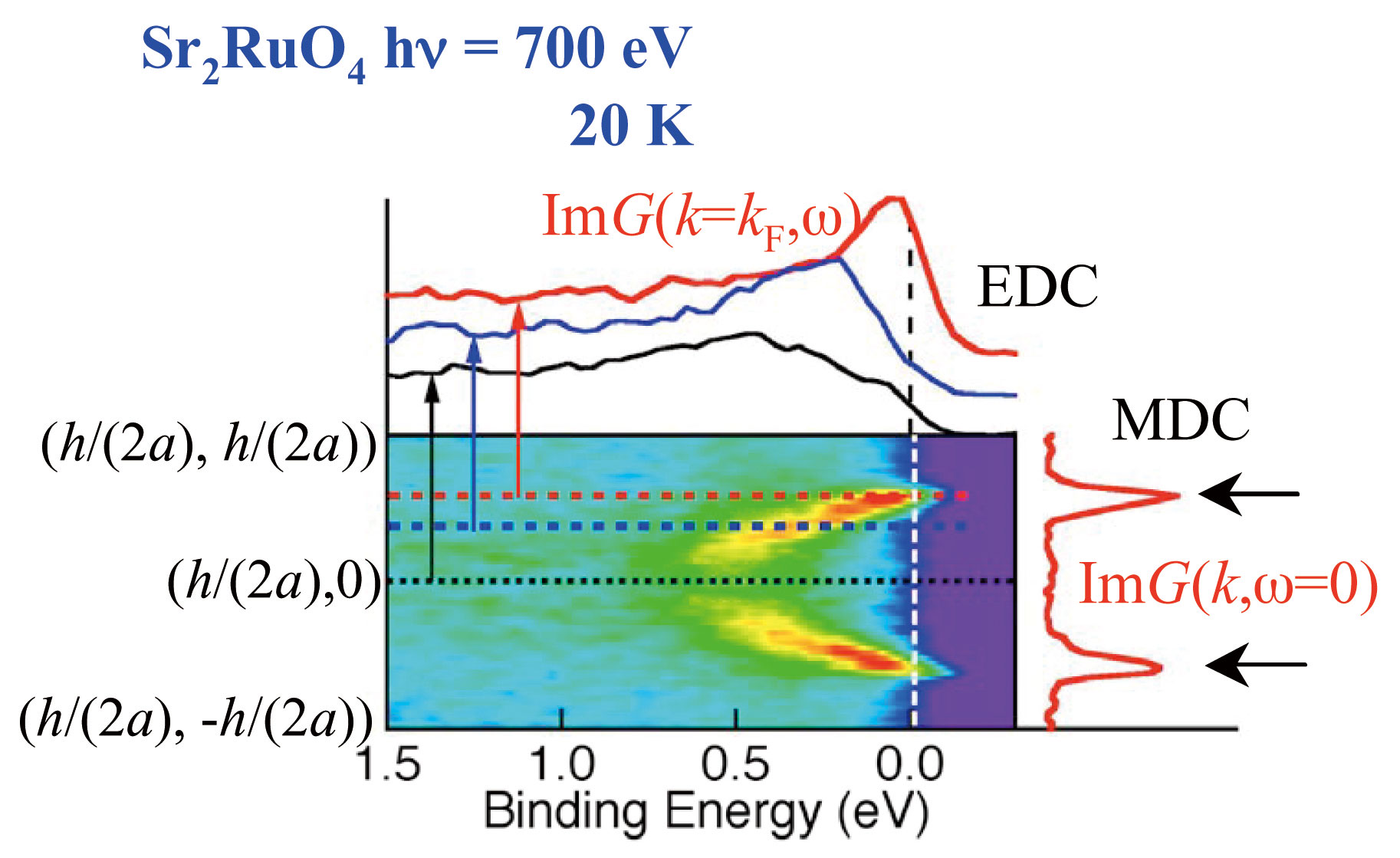
図10　Sr₂RuO₄の高エネルギーARPESデータの例^［13］[13] A. Sekiyama, S. Kasai, M. Tsunekawa, Y. Ishida, M. Sing, A. Irizawa, A. Yamasaki, S. Imada, T. Muro, Y. Saitoh, Y. Onuki, T. Kimura, Y. Tokura and S. Suga : Phys. Rev. B 70 (2004) 060506(R).。強度プロットの横軸が結合エネルギー、縦軸が運動量に該当する。左向き矢印は、対応する運動量がフェルミ面上にあること示す。


4．3次元強相関物質の軟X線角度分解光電子分光
　かなり前置きが長くなってしまったが、ここから今回測定したCeRu₂Ge₂の高エネルギー軟X線ARPESによる3次元フェルミ面探索について解説する。この物質はCeサイトに4f電子がほぼ1個つまった状態にある。希土類4f電子のエネルギーはフェルミ準位の近くだが、4f電子間のクーロン斥力（反発）が強いため、あたかも4f電子がサイト間の飛び移りが制限され各サイトに局在したかのような状態をとりやすい。一方で最近接サイトが構成する自由電子的な描像が比較的妥当な、動き回る遍歴的電子の軌道と4f軌道が空間的に重なるため、4f電子が一部伝導電子としての役割を果たすような遍歴性を持つ事があり得る。この「遍歴と局在の競合」が強相関物質の特長であり、面白い現象を引き起こす一つの原因となる。CeRu₂Ge₂はかなり4f電子が局在的で、8K以下で4f電子が孤立した磁気モーメントを持つかのような強磁性状態（磁石）になる^［4］[4] M. J.Besnus, A. Essaihi, N. Hamdaoui, G. Fischer, J. P. Kappler, A. Meyer, J. Pierre, P. Haen and P. Lejay : Physica 171B (1991) 350-352.。この強磁性相のフェルミ面はdHvA測定で判明している^［16,17］[16] C. A. King and G. G. Lonzarich : Physica B 171 (1991) 161-165.
[17] H. Ikezawa, H. Aoki, M. Takashita, C. J. Haworth, S. Uji, T. Terashima, K. Maezawa, R. Settai and Y. Onuki : Physica B 237 (1991) 210-211.が、常圧の消磁された常磁性状態でのフェルミ面は実験的に明らかでない。我々はこの物質に対して20Kの常磁性相で軟X線APRESをBL25SUで行い、試料内部のフェルミ面を3次元的に解明した。
　図11にhvを変えながら測定したΓ（0,0,0）−Z（0,0,h/c）方向のスペクトルを示す。hvが変わるとピークの結合エネルギー（binding energy）もそれに対応して変化し、前述の通り確かにエネルギーと面直方向運動量の関係が測定できている事が分かる。図12にはX（h/（2a）,h/（2a）,h/c）−Z（0,0,h/c）方向におけるX点近くの運動量分布（MDC）、Z点近くのZ−X方向のスペクトル（EDC）、Γ（0,0,0）−Z（0,0,h/c）方向のスペクトル（EDC）とバンド計算が予言した分散関係の定性的な描写（正確な分散は文献^［18］[18] H. Yamagami and A. Hasegawa : J. Phys. Soc. Jpn. 63 (1994) 2290-2302.を参照されたい）との比較を示す。このバンド計算は、Ce 4f電子が局在しフェルミ面形成に寄与しないと仮定（この場合CeRu₂Ge₂の常磁性状態は4f電子がないLaRu₂Ge₂と等価になる）して得られたものである^［18］[18] H. Yamagami and A. Hasegawa : J. Phys. Soc. Jpn. 63 (1994) 2290-2302.。ARPESはフェルミ準位E_Fより下のエネルギー領域の分散をトレースする。バンド計算の予言は実験を大まかには説明しているが、定性的な食い違いも見られる。例えばバンド計算ではZ点ではバンド1を含め5本のバンドに属する電子のエネルギーがE_Fより高い。これはZ点に対応する運動量でE_F程度のエネルギーを持つ電子は存在せず、その結果Z点でのスペクトル（EDC）はE_F近傍で全くピークを持たないことを予言する。しかし実験ではZに対応する運動量のスペクトルでE_F近傍0.15eVにピークが観測され、これに対応する電子が存在する事を意味する。X点ではバンド5に属する電子のエネルギーはE_Fより高く、やはりこれに対応した電子は存在しないのが計算結果だが、実験データ（MDC）ではバンド4に属する電子によるピークに加えてもう一つピークがあり、これがバンド5に属しX点に対応する運動量を持つ電子の存在を示す。この電子のエネルギーはX点ではE_Fよりわずかに低いが、X点から少し離れるにつれてE_Fに近づき、ついにはこの電子によるピークはMDCから消える。これはX−Z方向にバンド5の電子から形成されるフェルミ面がX点の近くで存在する事を示している。逆にZ点でのスペクトルでE_F近傍にピークを持つ事は、少なくとも1つのバンドの電子がZ点近傍でフェルミ面を形成しない事がわかる。このようなバンドが1つか複数かはこの場合Γ（0,0,0）−Z（0,0,h/c）方向のスペクトルを見ると判明するのだが、バンド1の電子がフェルミ面を形成しない事が分かった。




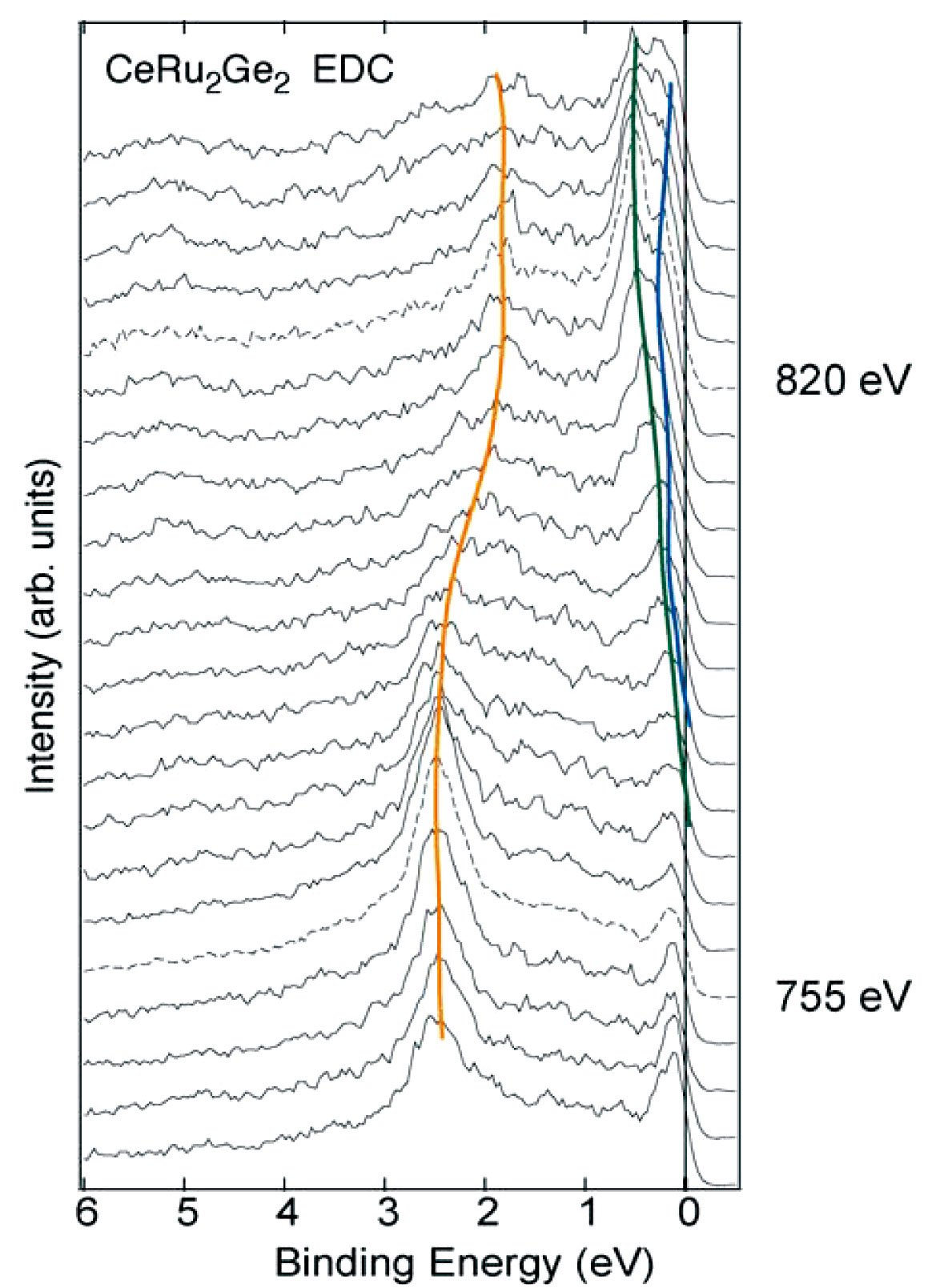
図11　CeRu₂Ge₂に対する（0,0,0）−（0,0,h/c）方向（図5右のΓ−Λ−Z方向に対応）の高エネルギーARPESスペクトル。カラーで示すような明確な分散が確認できる。右側の数字は横の破線スペクトルの励起エネルギーを示し、755eVが（0,0,h/c）点の、820eVが（0,0,0）点のスペクトルに対応する。




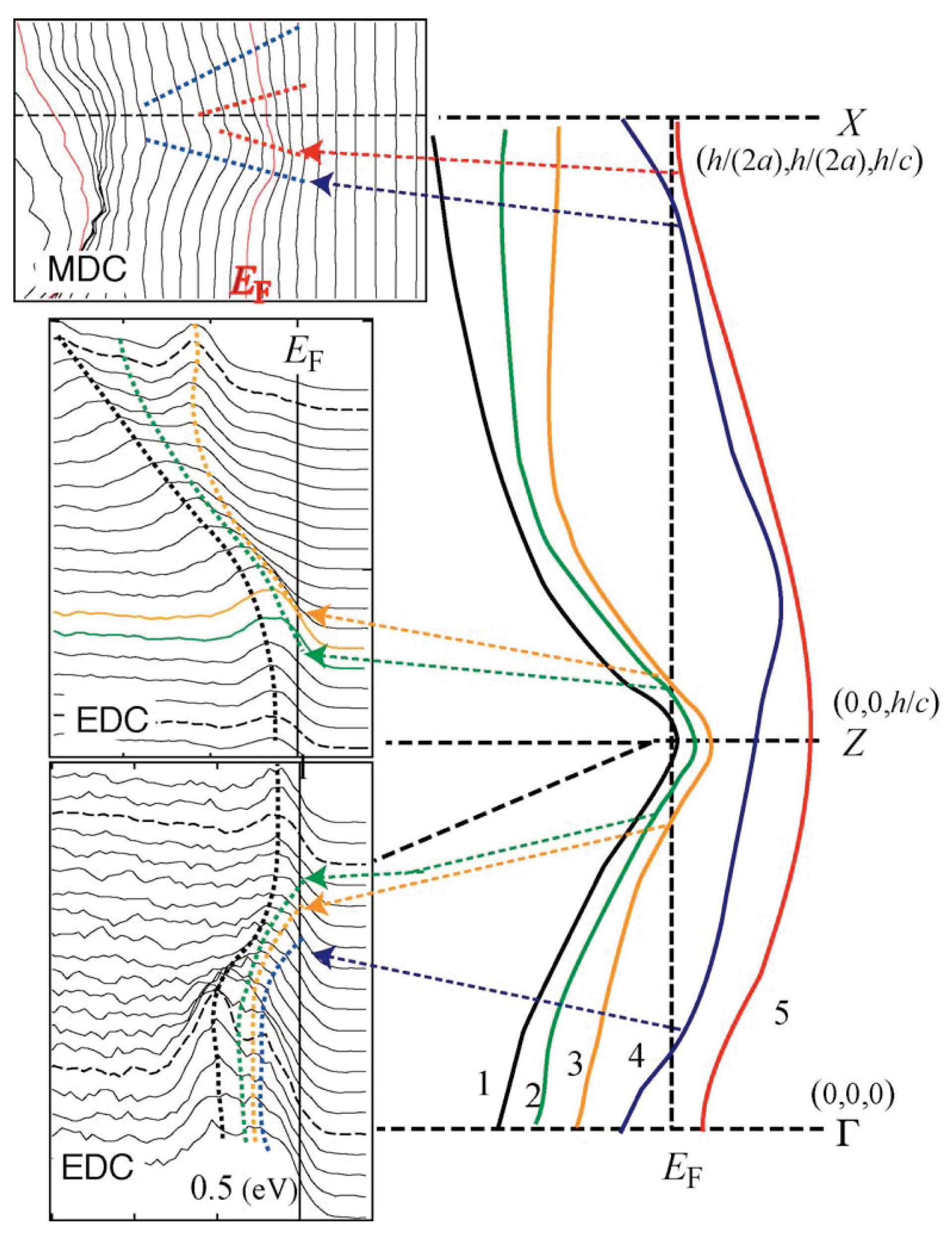
図12　CeRu₂Ge₂に対する（h/（2a）,h/（2a）,h/c）−（0,0,h/c）−（0,0,0）方向（図5右のX−Y−Z−∧−Γ方向に対応）の高エネルギーARPESスペクトル（左）とバンド計算^［18］[18] H. Yamagami and A. Hasegawa : J. Phys. Soc. Jpn. 63 (1994) 2290-2302.で導出された分散関係の定性的描写（右）。Z点のスペクトル（中パネル下部及び下パネル上部の破線スペクトル）ではフェルミ準位E_F近傍にピークがある事がわかる。矢印線は、光電子ピーク成分がほぼE_Fのところに来ている事を示す。



　以上のような解析を様々な運動量空間で得たスペクトルに対して行うとフェルミ面がどのようになっているかが分かる。図13に私達の測定で得られた伝導電子の運動量分布を示す。これは運動量空間で「横方向」と「縦方向」の断面を切り出したものに対応するため同時に観測したフェルミ面の断面をも示すことになる。これらの断面はhvと角度を少しずつ変えながら測定して得た物であり、固体内部のフェルミ面を正に3次元的に観測していることになる。これらの結果から3次元フェルミ面を書いたのが図14である。バンド計算はバンド1、2、3の電子による小さいラグビーボールのようなフェルミ面がZ点を中心として3個存在している事を予言するが、実際には2個しか存在せずバンド1の電子はフェルミ面を形成しない。バンド4の電子が作る饅頭のような形をしたフェルミ面は実験と計算は良い対応をみせている。またバンド5の電子が作るフェルミ面は計算によればΓ点を中心にしたドーナツ状のものと、p_z方向のX−X軸上にX点近傍でぶつぶつ途切れてタバコが縦に並んだようなフェルミ面になっている。実験ではドーナツ状のフェルミ面は確認できたが、p_z方向のX−X軸上のフェルミ面はX点で途切れることなくくびれた円筒状のフェルミ面になっている事が分かった。dHvA測定ではフェルミ面の断面積は高い精度で求まるが、そのフェルミ面が運動量空間内のどこにあるのかは実験的には分からない。本研究のように高エネルギーARPESでは運動量空間内でのフェルミ面の座標が分かるという利点がある。
　この物質の強磁性相でのフェルミ面はdHvA測定で分かっており、しかも実はバンド計算でよく説明できる^［16,17］[16] C. A. King and G. G. Lonzarich : Physica B 171 (1991) 161-165.
[17] H. Ikezawa, H. Aoki, M. Takashita, C. J. Haworth, S. Uji, T. Terashima, K. Maezawa, R. Settai and Y. Onuki : Physica B 237 (1991) 210-211.。今回の常磁性相における結果は一見それとは矛盾し、図14のように、あたかもフェルミ準位E_Fが少しだけ高いエネルギーにシフトしているかのように見える。これについて私達は以下のように考えている。強磁性相ではCe 4f電子が局在しているが、常磁性相ではCe 4f電子と周りの伝導電子が混じり合う事を通じてわずかではあるが4f電子の成分がフェルミ面形成に寄与、つまり殆どの4f成分は局在してもほんの一部分はフェルミ面を形成する役目を果たす。この時4f電子軌道そのものは変化せず、伝導電子の数が見かけ上増える。そうすると4f電子軌道を完全に局在化させたバンド計算では伝導電子の数が増える事でE_Fが少しだけ上昇する。それにより今回のようなフェルミ面になる。常磁性−強磁性転移の際には4f電子の"ほぼ完全な"局在化によって伝導電子の数は減り、その結果バンド1の電子がフェルミ面を形成し、バンド5の電子によるフェルミ面はp_z方向のX−X軸上の「くびれた円筒」からX点近傍でぶつぶつ途切れた「縦に並んだタバコ」のように変化するのではないかと思われる。




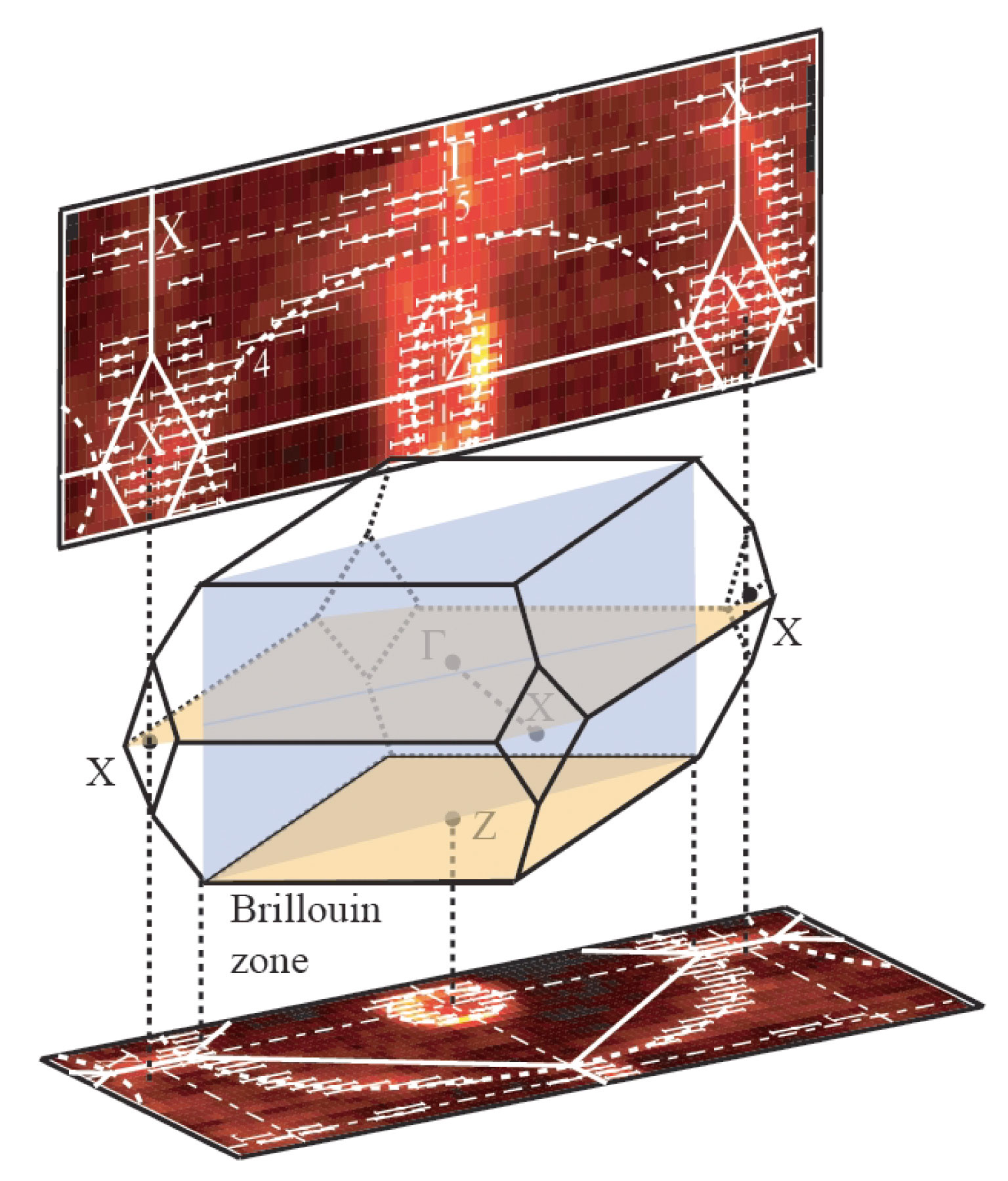
図13　CeRu₂Ge₂の軟X線角度分解光電子分光による3次元的フェルミ面マッピング。上の強度プロットがhvを変えながら測定して得た面直運動量方向を含む伝導電子の光電子強度を、下の強度プロットがhv一定で測定してZ点を含む運動量面内の伝導電子の光電子強度を示す。プロット中のエラーバー付きの白点はフェルミ面上の運動量を示す。




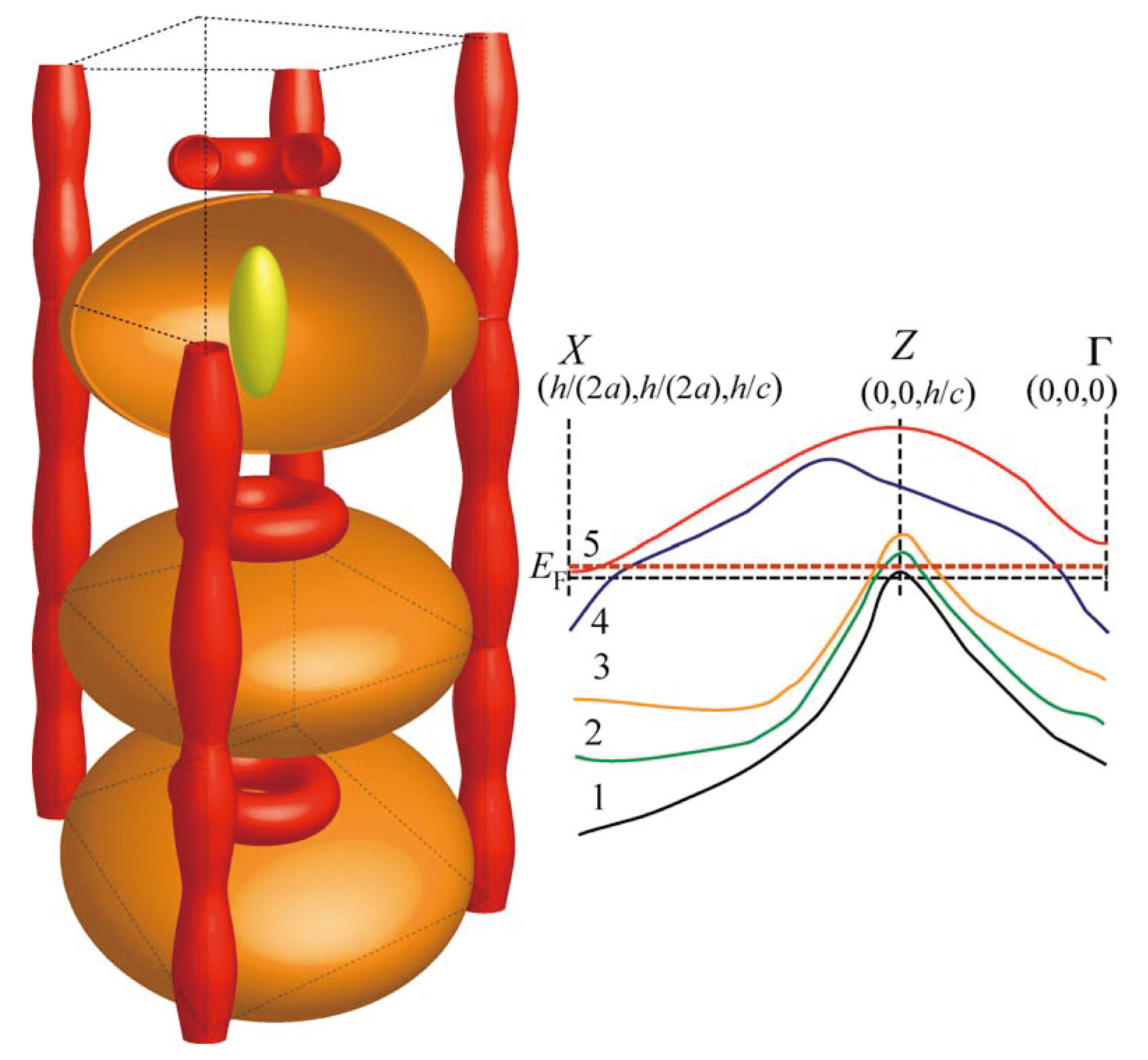
図14　軟X線角度分解光電子分光で得られた常圧常磁性相CeRu₂Ge₂の3次元フェルミ面（左）と電子構造（右）。ドーナツの中心がΓ点に、饅頭とラグビーボールの中心がZ点に、くびれた円筒のくびれた部分の中心がX点にそれぞれ対応する。常磁性相では計算に比べてフェルミ準位E_Fが上にシフトして赤い破線に位置しているかのような状態になっていると考えると実験をよく説明する。


5．おわりに
　今回紹介した軟X線角度分解光電子分光が今後新たなフェルミ面探索手法として広く発展しうる強力な実験手法になることは言うまでもない。現在はESRFでも類似の実験は可能であるが、それに加えSwiss Light Sourceでも2007年中に軟X線ARPESビームラインが完成しBL25SUの性能を上回る実験を可能にしようと奮闘中のようである。私達としてもまだこの実験技術にはさらなる改善が望ましい。明るさとビームタイムとの兼ね合いで、フェルミ面マッピングはかなり分解能を犠牲にして200meV程度で行っている。非共鳴条件で分解能100〜120meVでの実験は現在でも可能だが必要な時間はかなり増えるので、ある特定の一方向でのみの測定というように可能な測定は事実上限定される。私達は過去に文献［13］[13] A. Sekiyama, S. Kasai, M. Tsunekawa, Y. Ishida, M. Sing, A. Irizawa, A. Yamasaki, S. Imada, T. Muro, Y. Saitoh, Y. Onuki, T. Kimura, Y. Tokura and S. Suga : Phys. Rev. B 70 (2004) 060506(R).のデータ測定の際にはそのように実験した。軟X線領域でも分解能40〜50meVでの光電子分光は技術的に可能なはずで、将来的にはさらなる高分解能で測定できることを期待したい。また、今回は測定温度が一つだけであったが、相転移を起こす物質に対しては相転移温度の上下で測定し、フェルミ面がどう定性的に変化したかを調べるのには絶好の手段であり今後積極的に温度変化測定へと展開したい。またフェルミ面をみることで電子構造の次元性を調べるのに有効であることも間違いない。低次元電子系物質でも色々と面白い事が見えるのではないかと考えている。
　本研究は著者らのほか大貫惇睦教授（阪大理）及び阪大基礎工菅研究室の大学院生との共同研究であり、実験はSPring-8利用課題2004A6009、2004B0400を利用して行われた。関係者各位に感謝したい。



参考文献
[1] M. Yano, A. Sekiyama, H. Fujiwara, T. Saita, S. Imada, T. Muro, Y. Onuki and S. Suga : Phys. Rev. Lett. 98 (2007) 036405.
[2] 量子力学の啓蒙書としては、例えば並木美喜雄「量子力学入門(」岩波新書・新赤版、1992)など。
[3] ブロッホの定理については、キッテル「固体物 理学入門」(丸善)やザイマン「固体物性論の 基礎」(丸善)など固体物理/物性物理の教科書を見ていただきたい。
[4] M. J.Besnus, A. Essaihi, N. Hamdaoui, G. Fischer, J. P. Kappler, A. Meyer, J. Pierre, P. Haen and P. Lejay : Physica 171B (1991) 350-352.
[5] テキストとしては例えば津田惟雄、那須奎一郎、藤森淳、白鳥紀一「電気伝導性酸化物(改訂版)」(裳華房物性科学選書、1993)。
[6] テキストとしては例えば上田和夫、大貫惇睦「重い電子系の物理」(裳華房物理学選書23、 1998)。
[7] A. Damascelli, Z. Hussain and Z.-X Shen : Rev. Mod. Phys. 75 (2003) 473-541.
[8] A. Sekiyama, T. Iwasaki, K. Matsuda, Y. Saitoh, Y. Onuki and S. Suga : Nature 403 (2000) 396-398.
[9] A. Sekiyama, K. Kadono, K. Matsuda, T. Iwasaki, S. Ueda, S. Imada, S. Suga, R. Settai, H. Azuma, Y. Onuki and Y. Saitoh : J. Phys. Soc. Jpn. 69 (2000) 2771-2774.
[10] A. Sekiyama, S. Suga, S. Ueda, S. Imada, K. Matsuda, T. Iwasaki, M. Hedo, E. Yamamoto, Y. Haga, Y. Onuki, Y. Saitoh, T. Matsushita, T. Nakatani, M. Kotsugi, S. Tanaka and H. Harima : Solid State Commun. 121 (2002) 561-564.
[11] A. Sekiyama, H. Fujiwara, S. Imada, S. Suga, H. Eisaki, S. I. Uchida, K. Takegahara, H. Harima, Y. Saitoh, I. A. Nekrasov, G. Keller, D. E. Kondakov, A. V. Kozhevnikov, Th. Pruschke, K. Held, D. Vollhardt and V. I. Anisimov : Phys. Rev. Lett. 93 (2004) 156402.
[12] H. Wadati, A. Chikamatsu, M. Takizawa, R. Hashimoto, H. Kumigashira, T. Yoshida, T. Mizokawa, A. Fujimori, M. Oshima, M. Lippmaa, M. Kawasaki and H. Koinuma : Phys. Rev. B 74 (2006) 115114.
[13] A. Sekiyama, S. Kasai, M. Tsunekawa, Y. Ishida, M. Sing, A. Irizawa, A. Yamasaki, S. Imada, T. Muro, Y. Saitoh, Y. Onuki, T. Kimura, Y. Tokura and S. Suga : Phys. Rev. B 70 (2004) 060506(R).
[14] S. Suga, A. Shigemoto, A. Sekiyama, S. Imada, A Yamasaki, A. Irizawa, S. Kasai, Y. Saitoh, T. Muro, N. Tomita, K. Nasu, H. Eisaki and Y. Ueda : Phys. Rev. B 70 (2004) 155106.
[15] 菅滋正:SPring-8利用者情報 Vol.10, No.3 (2005) 194-199.
[16] C. A. King and G. G. Lonzarich : Physica B 171 (1991) 161-165.
[17] H. Ikezawa, H. Aoki, M. Takashita, C. J. Haworth, S. Uji, T. Terashima, K. Maezawa, R. Settai and Y. Onuki : Physica B 237 (1991) 210-211.
[18] H. Yamagami and A. Hasegawa : J. Phys. Soc. Jpn. 63 (1994) 2290-2302.

関山　　明　SEKIYAMA Akira
大阪大学大学院　基礎工学研究科　物質創成専攻　物性物理工学領域
〒560-8531　大阪府豊中市待兼山町1-3
TEL：06-6850-6422　FAX：06-6845-4632
e-mail : sekiyama@mp.es.osaka-u.ac.jp


矢野　正雄　　YANO Masao
大阪大学大学院　基礎工学研究科　物質創成専攻　物性物理工学領域
〒560-8531　大阪府豊中市待兼山町1-3
TEL：06-6850-6422　FAX：06-6845-4632
e-mail : yano@decima.mp.es.osaka-u.ac.jp


今田　　真　IMADA Shin
大阪大学大学院　基礎工学研究科　物質創成専攻　物性物理工学領域
〒560-8531　大阪府豊中市待兼山町1-3
TEL：06-6850-6421　FAX：06-6845-4632
e-mail : imada@mp.es.osaka-u.ac.jp


菅　　滋正　　SUGA Shigemasa
大阪大学大学院　基礎工学研究科　物質創成専攻　物性物理工学領域
〒560-8531　大阪府豊中市待兼山町1-3
TEL：06-6850-6420　FAX：06-6850-2850
e-mail : suga@mp.es.osaka-u.ac.jp


室　隆桂之　　MURO Takayuki
（財）高輝度光科学研究センター　利用研究促進部門
〒679-5198　兵庫県佐用郡佐用町光都1-1-1
TEL：0791-58-2750　FAX：0791-58-0830
e-mail : muro@spring8.or.jp