Volume 18, No.1 Pages 2 - 7
1. 最近の研究から/FROM LATEST RESEARCH
二つの超伝導ドームを持つ電子ドープ型鉄系超伝導体LaFeAsO1−x Hx
Two-dome Structure in Electron-doped Iron Arsenide Superconductor LaFeAsO1−x Hx
[1]東京工業大学 応用セラミックス研究所 Materials and Structures Laboratory, Tokyo Institute of Technology、[2]Department of Energy Science, Sungkyunkwan University
- Abstract
- LaFeAsO1−x Fxはホール面と電子面から構成される二次元フェルミ面を持っており、それらの形状がよく似ているため、これらのポケット間に働く強いネスティング;ある波数に対するフェルミ面の重なり具合、が母相の構造および磁気相転移を誘起する。O2−サイトをF−に置換することにより電子ドーピングすると、これらの相転移が抑制され0.05 < x < 0.2において最高でTC = 26 Kの超伝導が発現する。しかし、フッ素の酸素サイトへの固溶量がLaOFの生成によって制限されるために、電子ドーピングによって超伝導が完全に消失する過剰ドーピング領域をこれまで観察できていなかった。そこで我々は新しい電子ドーパントとして水素を用い、この問題の解決を試みた。フッ素の代替として水素を用いることによりx〜0.5まで電子をドープすることに成功し、LaFeAsO1−x Fxに見られていた超伝導ドーム(0.05 < x < 0.20)に加えて0.2 < x < 0.5に最高でTC = 36 Kを示す二つ目のドームを見出した。電子構造計算によれば、xの増加に従いフェルミ面のネスティングは単調に弱くなるが、鉄の三つの3d軌道、dxy、dyz、dzxから成るバンドがx = 0.36において縮退することが分かった。これらの結果から高いTCの発現にはバンド縮退が重要な寄与を果たしていると考えられる。
2008年初頭にLaFeAsO1−xFxが26 Kで超伝導転移を示すことが発見されて以降[1][1]Y. Kamihara, T. Watanabe, M. Hirano and H. Hosono: J. Am. Chem. Soc. 130 (2008) 3296-3297.、Feの正方格子をもつ様々な物質が研究されてきた[2-4][2]M. Rotter, M. Tegel and D. Johrendt: Phys. Rev. Lett. 101 (2008) 107006.
[3]X. Wang et al.: Solid State Commun. 148 (2008) 538-540.
[4]X. Zhu et al.: Phys. Rev. B 79 (2009) 220512.。現在、超伝導転移温度(TC)は1111系と呼ばれるLnFeAsO1−xFx (Ln = ランタノイド) において最高55 Kまで上昇している[5][5]Z. A. Ren et al.: Chin. Phys. Lett. 25 (2008) 2215-2216.。LaFeAsO1−xFxは常温で正方晶の常磁性金属であり、150 Kで正方晶ー斜方晶転移と反強磁性(AFM)転移を示す[6,7][6]C. de la Cruz et al.: Nature 453 (2008) 899-902.
[7]T. Nomura et al.: Supercond. Sci. Technol. 21 (2008) 125028.。これらの相転移をキャリアドーピングもしくは外圧の印加によって抑制すると、超伝導が発現する。AFM秩序近傍で超伝導が生じることから、その起源としてホール面と電子面間のネスティングによって生じるスピンのゆらぎが提案されており[8,9][8]I. I. Mazin, D. J. Singh, M. D. Johannes and M. H. Du: Phys. Rev. Lett. 101 (2008) 057003.
[9]K. Kuroki et al.: Phys. Rev. Lett. 101 (2008) 087004.、このモデルは過剰電子ドーピングによる超伝導の消失や、各超伝導体によるTCの違いをフェルミ面のネスティングから説明することに成功している[10][10]K. Kuroki, H. Usui, S. Onari, R. Arita and H. Aoki: Phys. Rev. B 79 (2009) 224511.。
しかし、これまで報告されているLnFeAsO1−xFx (Ln = La以外) の電子相図は酸素サイトに対するフッ素の固溶限界が低いためにドーピングによってTCが減少する領域が見られず不完全なものであった。最近、我々は酸素に対し高い固溶限界をもつ水素を用いて、(Ce, Sm)FeAsO1−xHxの合成とその完全な相図を報告してきた[11,12][11]T. Hanna et al.: Phys. Rev. B 84 (2011) 024521.
[12]S. Matsuishi et al.: Phys. Rev. B 85 (2012) 014514.。中性子回折実験とDFT計算から、水素は一価のアニオンとして排他的に酸素サイトを占有し、フッ素アニオンと同様に電子ドーパントとして働くことが分かった(O2− = H− + e−)。
LaFeAsO1−xFxと(Ce, Sm)FeAsO1−xHxの超伝導ドームを比較すると、La系は(Ce, Sm)系に比べ幅が狭く、また最高のTCも低い。加えてLaFeAsO1−xFxの常伝導状態における電気抵抗はフェルミ液体理論に従って温度に対し二乗で上昇するが[13][13]M. Imada, A. Fujimori and Y. Tokura: Rev. Mod. Phys. 70 (1998) 1039.、(Ce, Sm)FeAsO1−xHxは温度に対してリニアに抵抗が増加する非フェルミ液体的な挙動を示す。これらの違いが生じる原因として、フッ素置換では電子量が十分ではなく、LaFeAsOの真の物性を引き出せていない可能性が考えられる。
本研究では、Ln-1111のひな形物質であるLaFeAsOに対し、フッ素の代わりに水素を用いてその電気特性および磁気特性を調べた。また、SPring-8の高輝度放射光を用いた低温X線回折から求めた結晶構造を用いてDFT計算を行い、得られた超伝導の起源についても議論した。
Fig.1 a,bにLaFeAsO1−xHxの電気抵抗の温度依存性を示す。x = 0.01、0.04では150 K付近に構造、磁気相転移に起因する抵抗のキンクが見られる。xが増加すると相転移は抑制されx > 0.08で超伝導に起因する零抵抗が見られる。TCはx = 0.08で29 Kとなり、x = 0.21では18 Kまで減少する。さらに電子をドープすると、TCはx = 0.36で36 Kまで上昇し、抵抗は温度に対してリニアに変化する。Fig.1 e,fに各サンプルの体積磁気感受率の温度依存性を示す。金属Feの不純物があるため、すべての磁化率にはその強磁性成分がオフセットとして入っている。0.08 ≤ x ≤ 0.46ではいずれのサンプルも遮蔽体積分率が40%を超えているが、x = 0.53になると20%以下まで減少する。
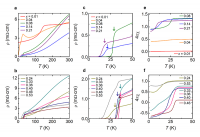
Fig.1 LaFeAsO1−xHxの電気磁気特性
(a, b)x = 0.01-0.21(a)および0.24-0.53(b)における電気抵抗の温度依存性。(c, d)x = 0.01-0.21(c)および0.24-0.53(d)におけるTC近傍におけるρ-T曲線の拡大図。矢印はオンセットTCを示している。(e, f)零磁場冷却、10 Oe下におけるx = 0.01-0.21(e)および0.24-0.53(f)の磁気感受率。
Fig.2 a-dにρ(T)曲線の圧力依存性を示す。x = 0.08、0.21および0.30では圧力に対しオンセットTCが単調に上昇するが、x = 0.46では常圧下のTC = 33 Kが2.7 GPaにおいて32 Kに減少する。常圧下でのTC (x) はx = 0.21周りに谷を持つが、それは高圧下で消失する。Fig.2 eにLaFeAsO1−xHxの常圧、および3 GPa下におけるTCと常圧下のTSをまとめて示す。x = 0.08とx = 0.36を頂点として二つの超伝導ドームが見て取れる。一つ目のドームは構造相転移とAFM転移に近接し、LaFeAsO1−xFxのドームとよく一致している。一方で、二つ目のドームは一つ目のドームの高ドープ側に隣接している。3 GPa下ではその二つのドームは合体し幅の広いドームとなり、その形状と最高TCはCeFeAsO1−xHxとよく一致する。これはLaFeAsO1−xHxの収縮率をLaFeAsO1−xFxと同等であると仮定すると3 GPa下ではa軸長が約1%収縮するために、3 GPa下のLaFeAsO1−xHxの格子定数が常圧下のCeFeAsO1−xHxの格子定数に近づいたことによるものと考えられる[12,15][12]S. Matsuishi et al.: Phys. Rev. B 85 (2012) 014514.
[15]H. Takahashi et al.: J. Phys. Soc. Jpn. 77 (2008) 78.。
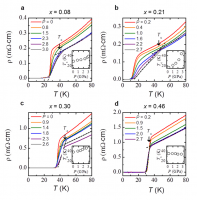
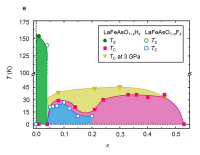
Fig.2 3 GPa以下におけるLaFeAsO1−xHxの電気抵抗の温度依存性とLaFeAsO1−x(H, F)xの相図
(a-d)静圧下におけるx = 0.08(a)、0.21(b)、0.30(c)および0.46(d)の電気抵抗の温度依存性。挿入図はTCの圧力依存性を示している。(e)LaFeAsO1−xHx(filled symbols)およびLaFeAsO1−xFx (open symbols) [14][14]C. Hess et al.: Europhys. Lett. 87 (2009) 17005.の電子相図。TCは超伝導転移の前後を外挿し、その交点とした。また電気抵抗の温度依存性に見られるキンクをTSとした。
ここでLa系と他のランタノイドを置換した1111系の物性の差異について考える。電気抵抗の温度依存性を比較するために、ρ = ρ0 + ATnで表されるべき乗フィッティングを行った。Fig.3 aに水素量xとその乗数nの関係を示す。n = 2となるフェルミ液体的な振る舞いはLa系の低ドープ領域のみに見られ、n < 2で示される非フェルミ液体的な振る舞いはLa系の高ドープ側および、他の1111系の全ドープ範囲で見られる。Fig.3 bは乗数nに対するTCの変化を示している。どの系においてもnが1に近づくにつれて、TCが最も高くなる。つまり、La系の二つ目のドームにおいて見られる非フェルミ液体化に伴うTCの上昇は1111系全般に見られる一般的な挙動であると言え、一方でLa系の一つ目のドームはLa系に特有の性質とみられる。Fig.3 c-fにLa、Ce、SmおよびGd-1111の超伝導ドームを示す。LaからGdへと格子が収縮するにつれて最高TCを示す電子量が連続的に低濃度側へシフトしていることが分かる。
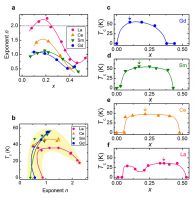
Fig.3 ランタノイドイオンの効果
(a)LaFeAsO1−xHx(pink circles)、Ce(yellow triangles)、Sm(green inverted triangles)とGd(blue pentagons)の乗数nとドープ量xの関係。乗数nはべき乗則ρ = ρ0 + ATnのフィッティングから求めた。破線はフェルミ液体状態(n = 2)を示している。(b)TC vs. n。(c-f)LnFeAsO1−xHx[Ln = La(pink circles)、Ce(yellow triangles)、Sm(green inverted triangles)とGd(blue pentagons)]のTCドーム。矢印は最高TCを示している。
LaFeAsO1−xHxが示す二つの超伝導ドームを理解するために、20 Kにおける結晶構造を用いて電子状態の計算を行った。酸素サイトを水素で置換した電子ドーピングは仮想結晶近似を用いて計算した。つまり、水素は電子ドーパントとしては疑似フッ素として振る舞い電子をFeAs層に供給すると考えた[12][12]S. Matsuishi et al.: Phys. Rev. B 85 (2012) 014514.。つまり、酸素サイト(Z = 8)をZ = 8 + xの核電荷をもつ仮想原子に置換した(ここでxは水素量を示す)。Fig.4 a-dに各電子量における二次元フェルミ面を示す。ここでx = 0.08は一つ目のドームの頂点、x = 0.21はTCの谷、x = 0.36は二つ目のドームの頂点、x = 0.4は過剰電子ドーピング領域になる。x = 0.08ではΓ点周りのホール面とM点周りの電子面のサイズがよく似ており、(π π)方向へのネスティングが強いと考えられる。xが増加すると、ホール面は単調に小さくなり、一方、電子面は単調に大きくなるために、ネスティングは弱くなる。一方、dxy軌道から成るホール面は電子量が増加してもその大きさが変わらない。黒木らは鉄面からのニクトゲンの高さが高くなると、このdxyホール面が大きくなると指摘している[10][10]K. Kuroki, H. Usui, S. Onari, R. Arita and H. Aoki: Phys. Rev. B 79 (2009) 224511.。今のケースの場合、電子をドープするとヒ素は徐々に鉄面から離れていくため、電子ドーピングによるホール面の縮小がキャンセルアウトされているものと思われる。

Fig.4 LaFeAsO1−xHxの電子構造
(a-d)LaFeAsO1−xHx[x = 0.08(a)、0.21(b)、0.36(c)および0.40(d)]の二次元フェルミ面。青矢印は(π π)方向のネスティングベクトルを示している。Feのdxy軌道とdyz,zx軌道の寄与はそれぞれ緑とピンクで色分けしている。(e)As-Fe-As角度とFe平面からのAsの高さ(hAs)の電子量依存性。角度とhAsは20 K下の放射光X線回折により求めた。(f-i)LaFeAsO1−xHx[x = 0.08(f)、0.21(g)、0.36(h)および0.40(i)]のバンド図[20][20]M. W. Haverkort, I. S. Elfimov, L. H. Tjeng, G. A. Sawatzky and A. Damascelli: Phys. Rev. Lett. 101 (2008) 026406.。(j)Γ点におけるFeの3dバンドエネルギーの電子量依存性。挿入図はx = 0.08のバンド図を示している[Γdxy(open green triangles)、Γanti-dxy(filled green inverted triangles)、Γdyz, zx(filled pink squares)はΓ点におけるFeの各3dバンドのエネルギー]。(k-n)LaFeAsO1−xHx[x = 0.08(k)、0.21(l)、0.36(m)および0.40(n)]のtotal-DOS(solid black line)、Feの3dxyのp-DOS(solid green line)、Feの3dyz, zxのp-DOS(pink green line)。Feの3dxyと3dyz, zx のp-DOSの和も示してある(dotted blue line)。
鉄系超伝導体の場合、ホール面と電子面間に働く強いネスティングがスピンゆらぎの原因と考えられている[8,9][8]I. I. Mazin, D. J. Singh, M. D. Johannes and M. H. Du: Phys. Rev. Lett. 101 (2008) 057003.
[9]K. Kuroki et al.: Phys. Rev. Lett. 101 (2008) 087004.。x = 0.08からx = 0.21にかけてのTCの減少はネスティングが弱くなったことによるスピンゆらぎの減少として理解できるかもしれないが、二つ目のドームを形成するx < 0.21のTCの上昇は同様のネスティングでは説明できない。Fig.4 f-iにEF付近のバンド構造を示す。
LaFeAsO1−x Hxはユニットセル中に二つの鉄を含むために、EF付近には鉄のバンドが計十本存在する。dxy軌道間の反結合性軌道に由来するバンド(今後anti-dxyと呼ぶ)は電子ドーピングに対して大きくエネルギーを下げ、結合性軌道に由来するバンドとx = 0.36で交差し、Γ点周りで鉄の3dxy、3dyz、3dzx軌道が三重縮退する。しかし、x = 0.40ではanti-dxyバンドと結合性のdyz,zxバンドの間で再構成が起こり新しいバンドを作る。Fig.4 eにおいてFe As4四面体中のAs-Fe-Asの角度がx = 0.33-0.46の高ドープ領域でも正四面体の109.5°よりもかなり離れていることに注意してほしい。つまり、Γ点周りのバンド縮退は鉄周りの局所構造の変化ではなく各軌道へドープされた電子の非対称占有によって引き起こされていると思われる。それらのバンドはΓ-Z方向にほとんど分散を持たないために、このバンド交差はDOS(EF)を増加させ、電子系を不安定化させる。このような場合、一般にはバンドヤーンテラーのような構造相転移が起こると考えられるが、今の場合0.08 ≤ x ≤ 0.40の範囲において少なくとも20 K以上ではそのような構造相転移は見られなかった。
Table1に上記で述べた超伝導ドームの特徴をまとめた。最も重要な課題は二つ目のドームの起源、つまり1111系の高いTCの起源は何なのかということである。TC直上の電気抵抗の温度依存性はx = 0.36に向かってT2からTに変化する。電子量の増加に従い、ホール面と電子面間のネスティングは単調に弱くなるため二つ目のドームに対するネスティングの寄与は大きくないと思われる。加えて、x = 0.36まわりでは鉄の3dxy、3dyz、3dzx軌道に由来するバンドの交差によりdensity of statesがEF付近に肩を持つ。これらの結果からバンド縮退が二つ目のドームの発現に重要な寄与を与えているように思われる。最近、母相の構造相転移近傍でずれ弾性率のソフト化が観測されたことをきっかけに新しいペアリングモデルが提案されている。このモデルは斜方晶への構造相転移によって3dyz、3dzx軌道の縮退が溶けると鉄のd軌道が秩序化し、その揺らぎも超伝導を誘起しうるというものである[16-18][16]M. Yoshizawa et al.: J. Phys. Soc. Jpn. 81 (2012) 024604.
[17]H. Kontani and S. Onari: Phys. Rev. Lett. 104 (2010) 157001.
[18]Y. Yanagi, Y. Yamakawa, N. Adachi and Y. Ōno: J. Phys. Soc. Jpn. 79 (2010) 123707.。もし、LaFeAsO1−xHxがこのモデルに従うとすると、電気抵抗が温度に対して直線的に上昇する現象は軌道ゆらぎによるキャリアの散乱として理解できるかもしれない。
| Dome | First | Second |
| x | 0.05 ≤ x ≤ 0.2 | 0.2 < x ≤ 0.5 |
| Exponent n | 2.0 ≤ n ≤ 2.3 | 0.7 ≤ n ≤ 2.0 |
| Tcmax | 29 K | 36 K |
| Tc-sensitivity to x | High | Low |
| Under high pressure | Unified | |
| FS nesting between | Strong | Weak |
| hole and electron pockets | ||
| DOS (EF) | No shoulder | shoulder |
最後になぜLa系においてのみ二つのドームが見られるのかについて考えてみる。Feの三つのバンドの縮退は、FeAs4四面体の正四面体からの歪による3dxy軌道と3dyz,zx軌道の間のエネルギー差が、ドープされた電子がこれらの軌道に非対称に占有されることによってキャンセルアウトされることで生じる。Laサイトをより小さなランタノイドイオンに置換すると、FeAs4四面体がより正四面体に近づくためにこのエネルギー差は小さくなる[19][19]P. Wang, Z. M. Stadnik, C. Wang, G. H. Cao and Z. A. Xu: J. Phys.:Condens. Matt. 22 (2010) 145701.。この正四面体からのずれはLa系が特に大きい。それ故Ce-Gd-1111ではこのバンド交差がx = 0.35よりもより少ない電子量で起こるはずである。その結果、La系の場合はバンド縮退による二つ目のドームはより高ドープ領域に現れるために、フェルミ面ネスティングによる一つ目のドームから分離して二つの超伝導ドームを形成したのではないかと思われる。
この軌道揺らぎに対する議論はDFT計算の結果をもとに行っている。今後このアイディアを実験的に証明するには単結晶の角度分解能方光電子分光実験や弾性率の測定が必要である。
謝辞
東京理科大学の福山秀敏教授には本研究を進めるに当たり有益なご議論を交わしていただいた。厚くお礼を申し上げる。
SPring-8での実験は2011A1142のビームタイムで得られた結果をもとにしている。実験にご協力いただいたJASRIの金延恩博士、理研の高田昌樹博士に厚くお礼を申し上げる。
また、本研究は世界最先端研究(FIRST)プログラムより補助を受けた。
参考文献
[1] Y. Kamihara, T. Watanabe, M. Hirano and H. Hosono: J. Am. Chem. Soc. 130 (2008) 3296-3297.
[2] M. Rotter, M. Tegel and D. Johrendt: Phys. Rev. Lett. 101 (2008) 107006.
[3] X. Wang et al.: Solid State Commun. 148 (2008) 538-540.
[4] X. Zhu et al.: Phys. Rev. B 79 (2009) 220512.
[5] Z. A. Ren et al.: Chin. Phys. Lett. 25 (2008) 2215-2216.
[6] C. de la Cruz et al.: Nature 453 (2008) 899-902.
[7] T. Nomura et al.: Supercond. Sci. Technol. 21 (2008) 125028.
[8] I. I. Mazin, D. J. Singh, M. D. Johannes and M. H. Du: Phys. Rev. Lett. 101 (2008) 057003.
[9] K. Kuroki et al.: Phys. Rev. Lett. 101 (2008) 087004.
[10] K. Kuroki, H. Usui, S. Onari, R. Arita and H. Aoki: Phys. Rev. B 79 (2009) 224511.
[11] T. Hanna et al.: Phys. Rev. B 84 (2011) 024521.
[12] S. Matsuishi et al.: Phys. Rev. B 85 (2012) 014514.
[13] M. Imada, A. Fujimori and Y. Tokura: Rev. Mod. Phys. 70 (1998) 1039.
[14] C. Hess et al.: Europhys. Lett. 87 (2009) 17005.
[15] H. Takahashi et al.: J. Phys. Soc. Jpn. 77 (2008) 78.
[16] M. Yoshizawa et al.: J. Phys. Soc. Jpn. 81 (2012) 024604.
[17] H. Kontani and S. Onari: Phys. Rev. Lett. 104 (2010) 157001.
[18] Y. Yanagi, Y. Yamakawa, N. Adachi and Y. Ōno: J. Phys. Soc. Jpn. 79 (2010) 123707.
[19] P. Wang, Z. M. Stadnik, C. Wang, G. H. Cao and Z. A. Xu: J. Phys.:Condens. Matt. 22 (2010) 145701.
[20] M. W. Haverkort, I. S. Elfimov, L. H. Tjeng, G. A. Sawatzky and A. Damascelli: Phys. Rev. Lett. 101 (2008) 026406.
東京工業大学 応用セラミックス研究所
〒226-8503 神奈川県横浜市緑区長津田町4259
TEL:045-924-5134
e-mail:s_iimura@lucid.msl.titech.ac.jp
東京工業大学 応用セラミックス研究所
〒226-8503 神奈川県横浜市緑区長津田町4259
TEL:045-924-5134
e-mail:satoru@lucid.msl.titech.ac.jp
東京工業大学 応用セラミックス研究所
〒226-8503 神奈川県横浜市緑区長津田町4259
TEL:045-924-5134
e-mail:h_sato@lucid.msl.titech.ac.jp
東京工業大学 応用セラミックス研究所
〒226-8503 神奈川県横浜市緑区長津田町4259
TEL:045-924-5134
e-mail:taku@lucid.msl.titech.ac.jp
東京工業大学 応用セラミックス研究所
〒226-8503 神奈川県横浜市緑区長津田町4259
TEL:045-924-5134
e-mail:muraba@lucid.msl.titech.ac.jp
Department of Energy Science, Sungkyunkwan University
300, Cheoncheon, Jangan-ku, Suwon, Korea
TEL:+81-31-299-4273
e-mail:sungwngkim@gmail.com
東京工業大学 応用セラミックス研究所
〒226-8503 神奈川県横浜市緑区長津田町4259
TEL:045-924-5134
e-mail:hosono@msl.titech.ac.jp








