Volume 09, No.3 Pages 203 - 213

◎特定利用課題採択名称
［課題名］：超臨界金属流体の静的・動的構造の解明
［実験責任者］：田村 剛三郎（京都大学）
［採択時の課題番号］：
　2000B0020−LD−np（BL04B1、BL28B2）
　2000B0583−LD−np（BL04B2）
　2001B3607−LD−np（BL35XU）
［実施BL／総シフト数］：
　BL04B1　計　72シフト（2000B〜2001B）
　BL28B2　計　72シフト（2002A〜2003A）
　BL04B2　計  174シフト（2000B〜2003A）
　BL35XU　計  144シフト（2001B〜2003A）
　総計  462シフト



1．はじめに
　超臨界流体が、ダイオキシン等の環境汚染物質を容易に分解するというので、脚光を浴びている。ある高圧機器メーカーの超臨界装置がベンチャー支援の対象になったという記事が新聞に出ていたり、別のメーカーは独自の超臨界装置を開発し、これが大いに販路を拡げ不況を乗り切る原動力になっているという話も聞く。このように、超臨界流体の有用性に着目した研究がますます盛んであることは大変に喜ばしいことである。しかしながらここでは、役に立つ超臨界流体というイメージから離れて、少し違った角度からこの特異な物質を眺めてみたい。
　超臨界流体とは何か。水を例にとればわかるように、圧力を加えていくと沸点は上昇する。さらに圧力を上げると沸点は上昇し続けるが、ある臨界圧力以上になるともはや沸騰が見られなくなり、液体とも気体とも区別のつかない超臨界流体と呼ばれる特異な状態が出現する。図１は、温度と圧力の平面上に固体、液体、気体の三相を表わしたものである。液体と気体の境界線が途切れるところに臨界点があり、その向こうに超臨界領域が広がる。ここで、矢印のように臨界点を迂回すると、液体から気体へと体積を連続的に、しかも千倍以上も膨張させることが可能になる。このことは平均原子間距離を十倍以上拡げることに相当する。物質に圧力を加え体積を収縮させることはできても、一様に膨張させることは容易でない。体積膨張が可能であること、これが超臨界流体の第一の特徴である。金属流体の場合には、この体積膨張過程で物性が大きく変化し、絶縁体へと転移する^［1］［1］F. Hensel and W. W. Warren Jr. : Fluid Metals (Princeton University Press, New Jersey, 1999).。




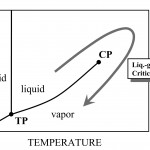
図1　相図


　原子や分子が凝縮して金属になるとき、どのような過程を経て金属になるのか、逆の見方をすれば、金属はどのように膨張・解離して絶縁体になるのか。これは、物質科学における最も基本的な問いである。この問いに答えるのに、超臨界金属流体は格好の場を提供する。
　我々は、これまで３年間、SPring-8の特定（長期）利用課題「超臨界金属流体の静的・動的構造の解明」を進めてきた。この研究計画は、代表的な液体金属である水銀、単体として唯一液体状態で半導体として振舞うセレン、さらにアルカリ金属ルビジウムを対象とし、Ｘ線回折測定により短・中距離構造について、Ｘ線小角散乱測定により密度のゆらぎ等の長距離構造について、さらにＸ線非弾性散乱測定によりダイナミクス、すなわち原子分子の離合集散の様相を明らかにするものである。本稿では、特定利用課題終了にあたり、これまでに得られた成果を紹介し、体積膨張に伴って金属から絶縁体へ転移するとき原子配列や動的振舞いに何が起こるかについて考える。


2．高圧容器の開発
　流体水銀、セレン、ルビジウムの臨界温度と圧力は、それぞれ、Hg（1478℃、1673bar）、Se（1615℃、385bar）、Rb（1744℃、124.5bar）であり、アルゴンや炭酸ガスのものに比べて非常に高い。このため、高圧容器、試料容器などの実験装置には特別の工夫が必要である。我々は、1700℃、ヘリウムガス圧縮による2000barまでの高温高圧下で放射光実験が可能な内熱型高圧容器を開発し、Ｘ線回折、Ｘ線小角散乱、Ｘ線非弾性散乱用に異なる３種類の高圧容器を製作した。高圧ガスの取り扱いに関する国（高圧ガス保安協会）の特別認可を得て、これらの装置をSPring-8の３つのビームラインBL04B1（BL28B2）、BL04B2、BL35XUに設置し、実験を行った。世界にある第三世代大型放射光施設の中で、SPring-8のビームラインは、超臨界金属流体の静的・動的構造研究が可能な唯一のビームラインである。
　図２は、Ｘ線回折測定用のビームラインBL28B2のハッチ内の写真を示す。ここで白色Ｘ線を用いたエネルギー分散型Ｘ線回折測定を行った。図３は、1700℃、2000barまで測定可能な内熱型高圧容器の側面図(a)および上面図(b)を示す。高圧容器は上下のフランジとシリンダーからなる。高圧容器中央にはサファイア製の試料容器に入れた水銀試料が置かれている。左側にあるBe製の高圧窓を通して白色Ｘ線を高圧容器内に導入し、試料により散乱されたＸ線を右側の７つ高圧窓から取り出し、半導体検出器を用いてエネルギー波高分析を行う。水銀を入れる試料容器は、高温の試料との反応性に耐え、かつＸ線に対して十分透明であるものでなければならない。このために我々は、0.15㎜の厚さまで薄く研磨したサファイア壁の間に、数十ミクロンの厚さの試料薄膜を安定に保持できるサファイア製試料容器を開発した。この高圧容器とサファイア容器を用いることにより超臨界金属流体の構造研究が可能になった^{［2, 3］}［2］K. Tamura, M. Inui and S. Hosokawa : Rev. Sci. Instrum., 70 (1999) 144.
［3］K. Tamura and S. Hosokawa : Phys. Rev. B 58 (1998) 9030. 。




図2　ビームラインBL28B2ハッチ内の写真




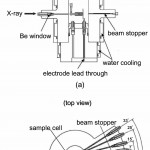
図3　Ｘ線回折用高圧容器の側面図(a)および上面図(b)



　図４は、ビームラインBL04B2におけるＸ線小角散乱実験用高圧容器の上面図を示す。Ｘ線回折用の高圧容器と違っている点は、高圧窓からの小角散乱の影響を除去するために、X線の入口、出口窓としてベリリウムの代わりに円柱形に加工した高純度人工ダイヤモンド（入口側：直径３㎜、厚さ２㎜、出口側：直径６㎜、厚さ2.5㎜）を用いていることである。Ｘ線源として38KeVの高エネルギー単色X線を用いた。




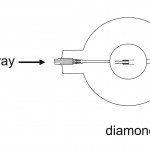
図4　Ｘ線小角散乱用高圧容器の上面図



　図５は、ビームラインBL35XUにおけるＸ線非弾性散乱用高圧容器の上面図を示す。複数の入射Ｘ線用ベリリウム窓と散乱Ｘ線を取り出すための複数のベリリウム窓を組み合わせることにより、散乱ベクトルを選択することができる。散乱ベクトルを連続的に変えることのできる大きな窓を設置することが望ましいが、2000barのガス圧下では技術的に容易ではない。また、国の特別認可を得ることが難しい。




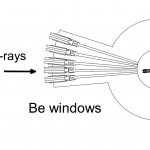
図5　Ｘ線非弾性散乱用高圧容器の上面図



3．流体水銀
　Ｘ線回折測定を行い^{［4, 5］}［4］K. Tamura, M. Inui, I. Nakaso, Y. Oh’ishi, K. Funakoshi and W. Utsumi : J. Phys.: Condens. Matter, 10 (1998) 11405.
［5］X. Hong, T. Matsusaka, M. Inui, D. Ishikawa, M. H. Kazi, K. Tamura, K. Funakoshi and W. Utsumi : J. Non-Cryst. Solids, 312-314 (2002) 284.、液体から超臨界領域を経て気体にいたる広い密度領域（13.6〜1.9gcm^-3）において、完成度の高い構造因子 S(Q)と二体分布関数g(r)を得ることができた^［6］［6］M. Inui, X. Hong and K. Tamura : Phys. Rev. B 68 (2003) 094108.。図６は、流体水銀のg(r)を示す。矢印は、金属−非金属転移が始まる9gcm^-3と臨界密度5.8gcm^-3を示す。g(r)を解析することによって得た配位数N_A、N_Bとg(r)の第一極大位置ｒ₁を密度に対してプロットしたものを図７に示す。N_AとN_Bの違いは、N_Aは最近接原子分布の中でもより近接位置にある原子の配位数を表し、N_Bはできるだけ広く原子を数えたことに相当する。N_Bは、液体から気体まで広い密度範囲にわたり大きくしかも原点に向かって直線的に減少している。この変化から、水銀が体積膨張するとき、原子間距離が増大するのではなく配位数が減少することが分かる。このことは、結晶の熱膨張と大きく異なる点である。液体の場合には、結晶性による拘束がないため、配置のエントロピーを増加させるべく空孔を生成しながら膨張すると考えることができる。しかし、近い方、すなわちN_Aは、金属領域においてほとんど直線的に減少するが、金属−非金属転移の始まる9gcm^-3あたりに近づくと直線からずれ、ほぼ一定値をとるようになる。さらに臨界密度を超えて気体領域に入ると、再び減少し始める。このN_Aの変化はｒ₁の密度変化とよく符合しており、最近接原子分布の中でもより近接位置にある原子数の減少が、金属−非金属転移に大きく関っていることが分かる。




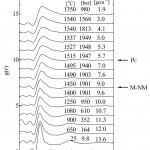
図6　流体水銀の二体分布関数g(r)




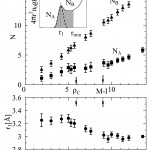
図7　流体水銀の配位数N_A、N_Bとg(r)の第一極大位置r₁の密度変化



　図８は、g(r)の第一極大の非対称性に着目して２つのガウス関数でフィットしたものであるが、金属−非金属転移の始まる9gcm^-3まで、近接位置にある原子の数が選択的に減少し、遠い方（影をつけた部分）の原子数は変わらない。また、詳細に調べた結果、ガウス関数の半値幅が9gcm^-3付近から増大することが分かった^［6］［6］M. Inui, X. Hong and K. Tamura : Phys. Rev. B 68 (2003) 094108.。このことは、金属−非金属転移に伴って配位数のゆらぎが存在することを示唆する。




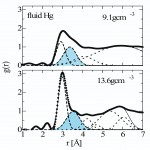
図8　g(r)のガウスフィット


　次に、Ｘ線小角散乱測定を行い、臨界散乱の観測に初めて成功した^［7-9］［7］K. Tamura and M. Inui : J. Phys. : Condens. Matter, 13 (2001) R337.
［8］K. Tamura, M. Inui, T. Matsusaka, D. Ishikawa, M. H. Kazi, X. Hong, M. Issiki and Y. Oh’ishi : J. Non-Cryst. Solids, 312-314 (2002) 269.
［9］M. Inui and K. Tamura : Z. Phys. Chem., 217 (2003) 1045.。図９は、一例として、1750barの一定圧力下で温度を変えることによって密度を変化させて得た最新の小角散乱スペクトルを示す。臨界密度5.8gcm^-3付近で臨界散乱が生じていることがわかる。これらの小角散乱スペクトルから、Ornstein-Zernikeの密度ゆらぎの式を用いて解析し、密度ゆらぎの大きさS(0)と相関長ξを求めることができる。図10は、臨界点から遠い1940barの一定圧力下および臨界点に近い1750barの圧力下で得たS(0)（四角）とξ（黒丸）を密度に対してプロットしたものである。S(0)は、臨界密度付近にピークがあり、ほぼ対称的な形をしているが、ξは半値幅が大きく、液体側に大きくすそを引いているのが特徴的である。S(0)とξの形の違いは、臨界点から離れた1940barのデータにおいて著しい。水やCO₂のような流体では、臨界点に近づくに従ってS(0)もξも大きくなり、共に臨界密度で極大を示し、ほぼ対称的な形をしており半値幅もほぼ同じである。これに対し、流体水銀では、密度9gcm^-3付近おいてS(0)が小さいにもかかわらずξの方には10Å程度の値が残っていることが大きな特徴である。このことは、金属−非金属転移領域において、臨界密度ゆらぎとは異なる新しいタイプのゆらぎ、中距離スケールの弱いゆらぎが存在することを示唆する。このことを詳しく見るために、液体構造論で重要な直接相関関数のフーリエ変換を波数のべきで展開したときの二次の係数ｃ₂が−ξ²/ρ S(0)で表されることに着目し、図10のS(0)とξを用いてｃ₂を計算してみた。ｃ₂の絶対値の密度変化を図11に示す。図10の二つの圧力下でのS(0)とξを比べてみて分かるように、形も値も大きく違っている。それにもかかわらず、図11のｃ₂の振る舞いは、臨界点から遠い場合（黒丸）と近い場合（四角）で極めてよく一致している。さらに興味深いことは、臨界密度5.8gcm^-3付近では特段何も起こらず、金属−非金属転移の起きる9gcm^-3付近で極大が見られることである。流体アルゴンの場合、Ornstein-Zernikeプロットの傾き（＝ξ²/ S(0)）は、臨界点に近づいてもほとんど変わらないことが知られている^［10］［10］H. E. Stanley : Introduction to phase transitions and critical phenomena, (Clalendon Press, Oxford, 1971).。このことは、直接相関関数が臨界領域においても短距離範囲にしかおよばないことをよく表している^［10］［10］H. E. Stanley : Introduction to phase transitions and critical phenomena, (Clalendon Press, Oxford, 1971).。流体水銀の場合、水銀原子が閉殻電子配置をしているため、低密度領域で希ガス的であると考えられてきた。水銀の臨界密度ゆらぎが、気体と非金属液体の間のゆらぎであると考えると、臨界領域における流体アルゴンのようにｃ₂がスムーズな変化をしても不思議ではない。破線は、比較のためにξ²/ S(0)が一定であるとしてｃ₂をプロットしたものである。すなわち、直接相関関数が密度変化をしない、例えば、高密度領域まで同じLennard-Jones ポテンシャルが使えるとしてプロットしたことに相当する。図のように、密度の増加に伴いｃ₂が破線からずれ、9gcm^-3付近で極大を示すことは、金属−非金属転移領域において直接相関関数が低密度領域のものと大きく違っていることを示している。このようなｃ₂における異常な振る舞いが、金属−非金属転移に伴うゆらぎが特異なものであることを明瞭に表している。このゆらぎは、臨界密度ゆらぎとは独立の、まさに金属−非金属転移の本質に関わるゆらぎである。




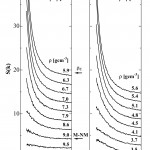
図９  流体水銀の小角散乱スペクトル




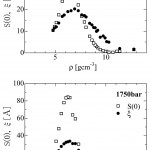
図10　流体水銀の密度ゆらぎの大きさS(0)とゆらぎの相関長ξの密度変化




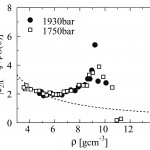
図11　流体水銀のｃ₂の密度変化


　それでは一体、どのようなゆらぎが生じているのか。臨界点近くでは、液体と気体の臨界密度ゆらぎを直接反映して、Ｘ線が見る電子密度分布には、密な領域と疎な領域で明瞭な違いが現れる。一方、金属‐非金属転移が起きる密度では、電子が局在する領域と非局在領域との間では電子密度に大きな差異はないであろう。臨界密度ゆらぎの密な領域を黒で塗り、疎な領域を白で表すとすると、金属−非金属転移領域のゆらぎは、いわば、濃いめの灰色（金属領域）と薄めの灰色（非金属領域）とで塗り分けられた薄墨模様をイメージすることができる。
　次に、Ｘ線非弾性散乱の結果について述べる。広い密度範囲、すなわち液体金属領域、超臨界領域、気体領域における動的構造因子S(Q, ω)を初めて得ることができ^［9］［9］M. Inui and K. Tamura : Z. Phys. Chem., 217 (2003) 1045.、これをもとに各領域において分散関係を求めることができた。液体金属領域では、金属−非金属転移に伴うfast sound mode の発見^［11］［11］D. Ishikawa, M. Inui, K. Matsuda, K. Tamura, A. Q. R. Baron, and S. Tutui : Phys. Rev. Lett., submitted.、超臨界領域では、臨界密度ゆらぎによる臨界遅延の観測、さらに気体領域では、高密度気体に残存する集団モードの観測^［12］［12］D. Ishikawa, M. Inui, K. Matsuda, K. Tamura, A. Q. R. Baron, S. Tutui, Y. Tanaka and T. Ishikawa : J.Phys. : Condens. Matter, 16 (2004) L45.など新しい事実が見出された。
　図12は、金属領域の密度13.6gcm^-3および金属−非金属転移の始まる9gcm^-3での分散関係を示す^［11］［11］D. Ishikawa, M. Inui, K. Matsuda, K. Tamura, A. Q. R. Baron, and S. Tutui : Phys. Rev. Lett., submitted.。四角印は、S(Q, ω)をモデル関数でフィットして求めた励起エネルギーを表し、一点鎖線は超音波測定から求めた音速の外挿線を示す^［13］［13］M. Yao, K. Okada, T. Aoki and H. Endo : J. Non-Cryst. Solids, 205-207 (1996) 274.。点線は、Ｑの小さい側の分散関係を延長したもので、その傾きから音速を見積もることができる。上段の図の実線はＸ線回折測定から求めたS(Q)、黒丸はS(Q, ω)をωで積分して得たS(Q)を表し、両者はよく一致している。密度13.6gcm^-3において、分散関係から見積もった音速は1700m/sであり、超音波測定から求めた音速に比べ17％程度速い。一方、9gcm^-3では、分散関係からの音速は1500m/sであり、超音波による音速490m/sに比べると３倍以上も速いという大変興味深い事実が判明した。
　図13は、分散関係から見積もった音速（ミクロな音速、四角印）と超音波測定から求めた音速^［13］［13］M. Yao, K. Okada, T. Aoki and H. Endo : J. Non-Cryst. Solids, 205-207 (1996) 274.（マクロな音速、破線）を密度に対してプロットしたものである。




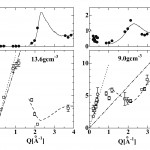
図12　金属‐非金属転移領域におけるω-Q分散関係と静的構造因子S(Q)





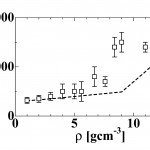
図13　分散関係から求めた音速（四角）と超音波測定による音速^[13]［13］M. Yao, K. Okada, T. Aoki and H. Endo : J. Non-Cryst. Solids, 205-207 (1996) 274.（破線）の密度変化



　図13から明らかなように、金属−非金属転移の始まる9gcm^-3付近で、ミクロな音速とマクロな音速の間に著しい違いが生じていることが分かる。金属−非金属転移領域において、なぜこのような速い音速（fast sound）が観測されるのであろうか。音速は、断熱圧縮率の平方根に逆比例する。Ｑが0.2から0.4Å⁻¹の範囲、すなわち10〜30Åの空間スケールに出現した速い音速の存在は、ミクロな断熱圧縮率が小さいことを意味する。このことは、ミクロな圧力のゆらぎが大きいことを意味する。また、圧力は二体ポテンシャル、特に斥力部分の形に依存するので、圧力のゆらぎが大きいことはポテンシャルのゆらぎが大きいことを意味する。それでは、なぜポテンシャルがゆらぐのか。Ｘ線小角散乱の実験から、金属−非金属転移領域において10Å程度の相関長をもつゆらぎの存在、すなわち10Å程度のスケールをもつ金属領域と非金属領域との間の空間的ゆらぎが起きていることが明らかになった。これらの領域は時間的にもゆらいでおり、金属領域は非金属領域へ、非金属領域は金属領域へと時々刻々入れ替わっているであろう。入れ替わりの周期あるいは緩和時間を正確に求めることは難しいが、S(Q, ω)の形から推定すると、その時間は1psあるいはそれより短いと考えられる。ある瞬間に、金属領域の水銀は伝導電子に遮蔽されたクーロンポテンシャルを感じるが、次の瞬間には、金属でなくなった領域の中でいわば Lennard-Jones ポテンシャルのような希ガス的ポテンシャルを感じることになるであろう。このように、ポテンシャルのゆらぎは、金属−非金属転移に伴うゆらぎに関係する。また、圧力のゆらぎは、金属領域と非金属領域とが入れ替わることにより10Å程度の空間で発生する。このように、fast sound は、金属−非金属転移に伴う水銀特有のゆらぎが原因で生じたものである。
　３つのビームラインを横断的に利用することによって、臨界密度ゆらぎ以外の、もうひとつのゆらぎを発見することができた。それは、金属−非金属転移に関わる非常に特異なゆらぎであり、隠されていたゆらぎである。
　そもそもなぜそのようなゆらぎが発生するのか。Ｘ線回折の結果で見たように、水銀が膨張するとき、配置のエントロピーを増すように配位数を減らす。さらに詳細に見ると、体積膨張と共に、最近接原子配置のうち遠い方の配位数は変わらず、近い方が選択的に減少してゆく。しかし、そのような構造変化がいつまでも持続するはずはなく、いずれ破綻をきたし、ミクロ構造の不安定性が発生するであろう。遠い方に位置している原子が近い方に移動したり、再び元の位置に戻ったりして、配位数のゆらぎとして構造不安定性が現れると考えることができる。Franz^［14］［14］J. R. Franz : Phys. Rev. Lett., 57 (1986) 889.は、配位数が３まで減少すると局所的にバンドギャップが現れ、この非金属状態は近隣に波及伝播すること、配位数が４になると金属的状態が現れ、それがまた近隣に波及伝播することを理論的に示した。この考え方に従えば、配位数のゆらぎは、金属領域と非金属領域との間のゆらぎを誘起することになる。水銀は配位数を減らしながらも金属状態をなんとか保持してゆくが、9gcm^-3まで膨張するとそれまでになかったミクロ構造の不安定性が発生し、この構造不安定性が絶縁体への転移の引き金になっていると考えられる。このゆらぎは、金属−非金属転移に伴って生ずるゆらぎであるという言い方は適当ではなく、まさに金属−非金属転移を引き起こすゆらぎである。また、流体水銀の金属−非金属転移が臨界点で起こらず臨界密度5.8gcm^-3よりはるかに密度の高い9gcm^-3で生じるのはなぜか、さらに金属−非金属転移が臨界密度ゆらぎと関係するのかどうかという疑問があった。実験結果に基づいたひとつの答えは、配位数を減らしながら膨張してゆき、結晶における一次相転移の前駆現象のようにある段階で必ずミクロ構造の不安定性が生じるが、その際、構造不安定性がどの段階で生じるかは物質によって異なり、融点近傍における液体の構造と電子状態の特徴によって決まるという考え方である。水銀の場合には、固体水銀の特異な最近接原子配置、すなわち最近接配置の中に近い部分と遠い部分があるという特徴が液体になっても残っている^［6］［6］M. Inui, X. Hong and K. Tamura : Phys. Rev. B 68 (2003) 094108.ことが、9gcm^-3という密度において金属−非金属転移が起きる元々の原因であると考えられる。流体水銀の金属−非金属転移は、臨界密度ゆらぎとは相関をもたない。
　以上、Ｘ線回折、Ｘ線小角散乱、Ｘ線非弾性散乱の測定により、当該分野共通の課題である流体水銀の金属−非金属転移の機構について、詳細なシナリオと言えないまでも、ピコ秒と数十Åの時間空間スケールでのあらすじは出来上がったと考えている。今後、小角および広角領域において得られた精度の高い構造因子をもとに、より精緻なＲＭＣシミュレーションを行い、実空間におけるゆらぎの特徴を抽出する予定である。


4．流体セレン
　Ｘ線回折測定を行い^{［15, 16］}［15］M. Inui, K. Tamura, I. Nakaso, Y. Oh’ishi, K. Funakoshi and W. Utsumi : J. Non-Cryst. Solids, 293-295 (2001) 446.
［16］X. Hong, M. Inui, K. Tamura, T. Matsuoka, D. Ishikawa and M. H. Kazi : J. Non-Cryst. Solids, 293-295 (2001) 446.、液体から気体に至る広い密度範囲で完成度の高いS(Q) とg(r)を得ることができた^［17］［17］M. Inui and K. Tamura : J. Non-Cryst. Solids, 312-314 (2002) 247.。図14に流体セレンのg(r)を示す。
　融点直上の液体セレンは２配位鎖状構造を持つ半導体である。１本の鎖には10万個のセレン原子が含まれるが、温度と圧力の増加と共に鎖は短くなり、臨界点近傍では10原子程度の短い鎖になる。このとき金属へ転移する。この半導体−金属転移に伴うミクロ構造の変化について明確な知見が得られた。すなわち、従来の予想のように３配位構造に変化するのではなく、２配位構造を保ったまま金属化し、共有結合距離はむしろ短くなる。さらに、気体中にセレン２原子分子が存在することを、Ｘ線回折測定法を用いて初めて実証することができた。このことを利用して、気体から超臨界金属流体へと凝集してゆく過程での回折パターンの変化を追跡することに成功し、セレン２原子分子が金属的性質をもつ短い鎖へと変化してゆく様子を捉えることができた。




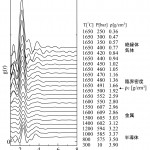
図14  流体セレンの二体分布関数 g(r)


　次に、Ｘ線小角散乱測定を行い、臨界散乱を観測することに初めて成功した^{［7, 8, 17］}［7］K. Tamura and M. Inui : J. Phys. : Condens. Matter, 13 (2001) R337.
［8］K. Tamura, M. Inui, T. Matsusaka, D. Ishikawa, M. H. Kazi, X. Hong, M. Issiki and Y. Oh’ishi : J. Non-Cryst. Solids, 312-314 (2002) 269.
［17］M. Inui and K. Tamura : J. Non-Cryst. Solids, 312-314 (2002) 247.。図15は、最新のデータを解析し、臨界点近傍の異なる温度におけるS(0)とξを密度に対してプロットしたものである。臨界密度1.85gcm^-3近傍にS(0)とξの極大があり、温度が下がり臨界温度（1615℃）に近づくとピークが大きくなっていることが分かる。また、本小角散乱実験により初めて、半導体−金属転移に伴う弱い密度ゆらぎを観測することができた（図16）。図16において、密度の大きい所は鎖状高分子構造をもつ半導体領域に対応するが、密度が減少し、約3.3gcm^-3になったところで金属化が始まる。ちょうど金属化が始まる密度で、S(0)とξが増大し始めることが分かる。また、ξには、密度が2.9から3.3gcm^-3の間で上に凸の傾向が現れている。これらのことは、流体セレンの中に、臨界密度ゆらぎとは違った、半導体−金属転移に伴う中距離スケールの弱いゆらぎが存在することを意味する。




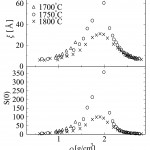
図15　流体セレンの超臨界領域における密度ゆらぎの大きさS(0)とゆらぎの相関長ξの密度変化




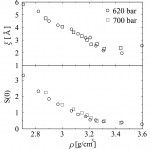
図16　流体セレンの半導体‐金属転移領域における密度ゆらぎの大きさS(0)とゆらぎの相関長ξの密度変化



5．流体ルビジウム
　水銀やセレンの実験に用いてきたサファイア試料容器は、反応性の強いアルカリ金属には用いることができない。我々は、1500℃を超える高温で使用可能なモリブデン製試料容器を新たに開発した^［18］［18］K. Matsuda, K. Tamura, M. Katoh and M. Inui : Rev. Sci. Instrum., 75 (2004) 709.（図17）。上段右の写真は、流体ルビジウムを両側から保持する厚み40μの単結晶モリブデンディスクからのラウエスポットを示す。これを用いて初めて超臨界領域までのＸ線回折測定を行うことができた。その結果、二体分布関数の第一ピークが、体積膨張にもかかわらず1200℃以上で急に距離の短い方へシフトするという予想外の事実が明らかになった。この実験結果を下條ら^［19］［19］F. Shimojo, Y. Zempo, K. Hoshino and M. Watabe : Phys. Rev. B 52 (1994) 9320.の第一原理分子動力学シミュレーションの結果と比較することにより、膨張してゆく流体ルビジウム中に、非常に早い段階で、すなわち1200℃という臨界温度（1744℃）から遠く離れた液体金属領域において、二原子分子Rb₂が出現するという興味深い事実が明らかになった。液体金属中に出現したRb₂は、気体中に存在する安定なものとは異なり、伝導電子による遮蔽を受けて不安定で寿命の短い分子であると考えられる。何故このようなRb₂が現れるのか。流体ルビジウムの場合にも、水銀のように体積膨張に伴って配位数が減少するが、この特異な液体中のRb₂もやはり、配位数の減少に伴う構造不安定性によって生じたものであり、また、構造不安定性が起こるのは、融点での液体ルビジウムの構造、さらには、固体ルビジウムがｂｃｃという疎な構造をとるということに原因があると考えている。そこでは、中距離スケールのゆらぎが発生している可能性がある。どのようなゆらぎが生じているか、ゆらぎの空間的・時間的振舞いを調べることは大変興味深い（ごく最近Ｘ線小角散乱の実験に成功し、現在データ解析を行っているところである）。流体ルビジウムの構造研究は、これまで単純金属であると考えられてきたアルカリ金属に対する視点を大きく変えるであろう。




図17  流体アルカリ金属の構造研究用に開発したモリブデン試料容器


　最近、米国のWeirらによる水素分子の爆縮実験により、3000K、1.4Mbarという超高温超高圧下で、水素が金属（流体金属水素）になることが明らかにされ^［20］［20］S. T. Weir, A. C. Mitcell and W. J. Nellis : Phys. Rev. Lett., 76 (1996) 1860.、水素がアルカリ金属の仲間であることが初めて示された。水素分子の圧縮過程は、本研究のアルカリ金属流体の膨張過程のまさに逆のプロセスである。したがって、膨張するアルカリ金属流体の構造研究は、現在のところ実施が困難である流体金属水素と密接に関わる構造研究を行っていることになる。この意味で、本研究は木星の内部構造に関わる研究でもある。木星内部には流体金属水素が存在し、それが木星特有の強い磁場を生じていると考えられている。水素分子が中心に向かって圧縮されるときどのように金属化するか、木星の深いところで金属へ転移するのか、あるいは、浅いところで金属になるかは、木星磁場の起源に関わる重要な問題である。本研究は、この問題に対して物質科学の立場から確かな指針を与えることになるであろう。また、本研究は、材料としての金属水素、すなわち、室温超伝導体であると予想され、核融合や高効率エネルギー源として将来必ず重要な意味を持ってくる金属水素に大きく関わりをもつ。


6．おわりに
　高圧ガス特別設備を３つのビームラインに設置し、このような実験を遂行することができたのは、JASRIの方々、ビームライン担当者、安全管理室、原研、理研の方々のご支援によるものである。それがなければこの研究を進めることはできなかったであろう。本当に多くの方々にご支援をいただいた。ここに深く感謝する。また、広島大学の乾雅祝助教授をはじめ、これまで共同研究を行ってきた多くの方々にお礼を申し上げる。神戸製鋼所、高圧システム、理学電機の各社には技術的な面で大変お世話になった。本長期利用課題は、文部科学省科研費特別推進研究(2)「放射光を用いた超臨界金属流体の静的・動的構造の解明」（平成11〜15年度）と平行して進められたことを付記する。



参考文献
［1］F. Hensel and W. W. Warren Jr. : Fluid Metals (Princeton University Press, New Jersey, 1999).
［2］K. Tamura, M. Inui and S. Hosokawa : Rev. Sci. Instrum., 70 (1999) 144.
［3］K. Tamura and S. Hosokawa : Phys. Rev. B 58 (1998) 9030.
［4］K. Tamura, M. Inui, I. Nakaso, Y. Oh’ishi, K. Funakoshi and W. Utsumi : J. Phys.: Condens. Matter, 10 (1998) 11405.
［5］X. Hong, T. Matsusaka, M. Inui, D. Ishikawa, M. H. Kazi, K. Tamura, K. Funakoshi and W. Utsumi : J. Non-Cryst. Solids, 312-314 (2002) 284.
［6］M. Inui, X. Hong and K. Tamura : Phys. Rev. B 68 (2003) 094108.
［7］K. Tamura and M. Inui : J. Phys. : Condens. Matter, 13 (2001) R337.
［8］K. Tamura, M. Inui, T. Matsusaka, D. Ishikawa, M. H. Kazi, X. Hong, M. Issiki and Y. Oh’ishi : J. Non-Cryst. Solids, 312-314 (2002) 269.
［9］M. Inui and K. Tamura : Z. Phys. Chem., 217 (2003) 1045.
［10］H. E. Stanley : Introduction to phase transitions and critical phenomena, (Clalendon Press, Oxford, 1971).
［11］D. Ishikawa, M. Inui, K. Matsuda, K. Tamura, A. Q. R. Baron, and S. Tutui : Phys. Rev. Lett., submitted.
［12］D. Ishikawa, M. Inui, K. Matsuda, K. Tamura, A. Q. R. Baron, S. Tutui, Y. Tanaka and T. Ishikawa : J.Phys. : Condens. Matter, 16 (2004) L45.
［13］M. Yao, K. Okada, T. Aoki and H. Endo : J. Non-Cryst. Solids, 205-207 (1996) 274.
［14］J. R. Franz : Phys. Rev. Lett., 57 (1986) 889.
［15］M. Inui, K. Tamura, I. Nakaso, Y. Oh’ishi, K. Funakoshi and W. Utsumi : J. Non-Cryst. Solids, 293-295 (2001) 446.
［16］X. Hong, M. Inui, K. Tamura, T. Matsuoka, D. Ishikawa and M. H. Kazi : J. Non-Cryst. Solids, 293-295 (2001) 446.
［17］M. Inui and K. Tamura : J. Non-Cryst. Solids, 312-314 (2002) 247.
［18］K. Matsuda, K. Tamura, M. Katoh and M. Inui :  Rev. Sci. Instrum., 75 (2004) 709.
［19］F. Shimojo, Y. Zempo, K. Hoshino and M. Watabe : Phys. Rev. B 52 (1994) 9320.
［20］S. T. Weir, A. C. Mitcell and W. J. Nellis : Phys. Rev. Lett., 76 (1996) 1860.




田村　剛三郎　TAMURA  Kozaburo
京都大学　工学研究科　材料工学専攻　教授
〒606-8501　京都市左京区吉田本町
TEL：075-753-5462　FAX：075-753-4978
e-mail：tamura@materials.mbox.media.kyoto-u.ac.jp