Volume 09, No.1 Pages 36 - 41

1．はじめに
　20世紀の物質科学の進展の一つに、炭素や珪素を中心とするナノクラスタ物質の発展がある。また、半導体工学の進展により種々のシリコンの純粋な同位体元素が得られるようになってきた。ナノクラスタ物質に同位体元素を適用した場合、物質の物性の基礎を詳細に検討することができる場合がある。また、同じ種類の元素から作り出される固体でも、純粋な同位体を用いて合成される構造体は、将来デバイスとしての種々の応用が考えられる。本書では、シリコンの同位体元素を多面体ナノクラスタに適用した物質を用いた超伝導機構解明の研究とシリコン同位体構造体の量子コンピュータへの発展を紹介する。


2．多面体ナノクラスタ
　原子が数個から数十個集合すると、ある特定の個数の集合体において、結晶とは異なる構造が形成されることがある。このような物質を一般にクラスタと呼ぶ。このようなクラスタの中でも、特に1990年代に物性実験ができるようになったC₆₀は代表的な物質である。同様の多面体を基本とする結晶は、珪素元素でも形成される。図１に示すように、珪素元素の場合には炭素元素とは異なり、5員環から構成される正12面体を多く含むSi₂₀、Si₂₄、Si₂₈が基本構造であり、共有結合を介して結合した種々の共有結合結晶ができる。




図1　珪素元素から作り出される種々のクラスタ


　C₆₀クラスタ結晶およびSi₂₀結晶は多面体ネットワーク物質と総称され、４族元素から数多く形成される。これは、IV族元素は、結合様式が柔軟性で、多様な結合角度に対応した物質構造のエネルギー安定性が生まれるからである。多面体クラスタを形成する現象は、高圧下の水およびIII−Ⅴ族元素を中心とするB、Al、C、Si、Ge、Sn、Pなどの元素に多くみられる ^[1-3] ［1］T. Blunier, J. Chapellaz, J. Schwander, B. Stauffer and D.Raynaud : Nature, 374 (1995) 46-49.
［2］E. J. Brook, T. Sowers, and J. Orchardo
: Science, 273 (1996) 1087-1091.
［3］J.S. Kasper, P. Hagenmuller, M. Pouchard and C. Cros : Science, 150 (1965) 1713.。
　第２周期の元素であるCの場合には、多面体クラスタの安定性はsp²軌道混成を主体とした構造であるのに対して、第3-5周期のSi、Ge、Sn 元素の場合には、sp³軌道混成を主とした構造である ^[4] ［4］H. Kawaji, H. Horie, S. Yamanaka and M. Ishikawa : Phys. Rev. Lett. 74 (1995) 1427.。その結果として、安定な多面体クラスタ構造は、C 元素の場合にはC₆₀の構造が最小単位になり、それより小さい炭素数で構成される多面体クラスタは不安定である。一方、多くのSi、Ge、Sn 元素を構成要素とする多面体クラスタは、結合角がsp³軌道混成の結合角である109.8 度近傍を示す、正12面体クラスタが安定な構造となる。


3．クラスタネットワーク物質の階層構造
　このようなクラスタが構成要素となり形成される結晶の電子状態は、クラスタ特有の性質を色濃く反映する。従って、結晶構造およびその電子状態はクラスタを基本要素とした階層的な構造として理解することができる。C₆₀を基本とする結晶は、C₆₀クラスタが閉殻構造を有するために、ファンデワールス結晶として分類されるのに対して、（IV＝S, Ge, Sn）₂₀を基本要素とする結晶は共有結合結晶として分類される。
　説明のために、Si₂₀多面体クラスタを基本として作り出される代表的なクラスレート結晶の階層構造を、図２に示した。結晶はブラベ格子である立方体の各頂点と中心にIV₂₀を配置した構造となっている。中心の正12面体クラスタは、頂点に置かれた正12面体クラスタと比較すると、90度回転した配置をとっていて、結晶学的には単純立方晶（P）である。



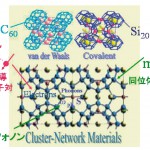
図2　クラスタ結晶の階層構造


　この構造は、Nb₃Sn などの無機物質で有名なA15 構造と総称される結晶構造と比較すると理解しやすい。立方体の頂点および中心に存在し、内部に他元素を内包する１格子当たり２個の正12面体クラスタA@IV₂₀をSnに（＠：内包を意味する）、立方体の面上に存在する１格子当たり６個の元素B@IV₂₄（クラスタ構造で考えると14面体クラスタIV₂₄の内部に内包されている元素）をNbと対応させれば、全く同じ構造である。実際のクラスレート化合物の単位胞では、この他に正12 面体クラスタを結ぶ位置に、２つの格子面を共有する形で単位胞当たりに６個の元素が配置され、計46 個の原子数で完全結晶としてのブラベ格子を形成している。
　ここで述べたクラスタ結晶を別の観点でみることもできる。すなわち、正12面体クラスタをこの格子から除くと正14面体クラスタが残り、クラスレートは、正14面体クラスタから形成されていると考える事もできる。このような見方に立脚すると、CおよびDの46個の原子のうちCサイトの６個の原子は、前述したように14面体クラスタの構成元素の一部でもある。したがって、14面体クラスタは［20×Si+4×IV］と表記する事もできる。


4．同位体と超伝導の機構
　元素は原子核を構成する中性子および陽子とその核の周りを量子力学的な確率に従って電子雲として取り囲む電子から構成されている。原子の多くの性質は、この核の回りの電子の個数により決まる。元素には中性子の個数が異なる幾つかの元素が存在する。これが同位体元素である。元素の質量は主に核を構成する中性子の質量（m_n）と陽子の質量（m_p）により決定されるので、同じ元素でも質量が異なる元素が存在することになる。図３に示すように、有機物質の重要な構成元素である炭素元素の場合には、主に質量数が12（¹²C）と13（¹³C）の同位体が存在して、自然界には、¹²Cの炭素が98.9%存在する。また、半導体として重要な珪素元素の場合には、質量数が²⁸Si、²⁹Si、³⁰Siの同位体が良く知られていて、天然の珪素元素は²⁸Siを92.2%含んでいる。



図3　炭素および珪素の主要な同位体


　新しい超伝導が出現した場合、その機構を理解することは重要なことである。1990年代後半に出現したC₆₀を基本構造とする超伝導体とSi₂₀超を基本構造とする伝導体の２種類のクラスタ系超伝導体は重要である。C₆₀系超伝導体は、超伝導臨界温度が非常に高いこと、Si₂₀系超伝導体に関しては、純粋なシリコンネットワークで初めての超伝導体であり、歴史的に非常に重要な超伝導体であると言える。
　超伝導体の機構を知るためには、同位体効果は重要な実験である。超伝導機構として重要なBCS理論に立脚した場合、フォノンが超伝導とどのように関係するかが重要な鍵であり、他の物性量を変化させずにフォノンを変化させる純粋な同位体から作られる2種類の物質を合成する必要がある。C₆₀系超伝導体に関しては1992年に幾つかのグループによりC₆₀超伝導体に関する同位体効果の実験やＮＭＲの実験が行われ、それらの測定結果から、高周波領域のフォノン（〜1000K）が主に介在するBCSタイプの超伝導体であるという認識が得られている。しかし、Si₂₀系の超伝導体に関しては、これまでその機構を理解するための重要な同位体効果の実験がなされていなかった。この理由は、¹³C同位体に対して³⁰Si同位体は非常に入手し難いこと、ならびに組成を制御した合成が極めて困難であったからである。そのために、Si₄₆系超伝導体がはじめて報告されたのが1995年であるにもかかわらず ^[4] ［4］H. Kawaji, H. Horie, S. Yamanaka and M. Ishikawa : Phys. Rev. Lett. 74 (1995) 1427.、８年もの間そのような実験が無かった。今回²⁸Siおよび³⁰Siの同位体で色分けされた図４のような２種類の超伝導体物質を合成した ^[5]［5］K. Tanigaki, T. Shimizu, K. M. Itho, J. Teraoka, Y. Moritomo and S. Yamanaka : Nature Materials, 2 (2003) 653-655.。




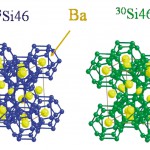
図4　²⁸Si₂₀および³⁰Si₂₀から構成されるシリコン



　図５に示すように、今回の同位体を用いた超伝導同位体効果の実験の結果、α=0.08〜0.12の値が観測された、この観測値とラマンによるフォノンの観測周波数から誤差を十分に考慮したMcMillanの式にもとづく解析を行い、物理変数λ＝0.79〜1.2、µ*=0.23〜0.31が得られた。決定されたµ*はかなり大きい値であるが、その他の実験結果と同位体効果の実験誤差を考慮して、本超伝導体の機構が、フォノンを介在とするBCSの上限に位置すると結論された。米国ペンシルバニア州立大学、V. H. Crepsi教授は、C系とSi系の２種類の超伝導体がどちらもBCS超伝導体の仲間入りをしたと研究を高く評価している ^[6] ［6］V. H. Crepsi : Nature Materials 2 (2003) 650-651.。




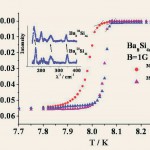
図5　超伝導同位体効果



　重要なことは、C₆₀系超伝導体の場合には、空気中で不安定な物質であるため高精度な比熱の実験などが行われていないが、今回の実験では、図６に示すように超伝導臨界温度での比熱の飛び、臨界温度以下の比熱の温度関数、磁化率測定など、詳細な種々の実験を行い、その結果として、総合的な判断から本物質系がフォノンを介在とするBCS超伝導体に分類されると、結論されたことである。Tc以下での比熱の温度依存性の観点から、この超伝導体がs波の超伝導体であることも明確にされた。




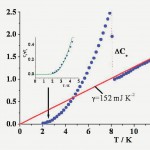
図6　Ba₈Si₄₆に関する比熱



　今回の、Siクラスタ系超伝導機構を決定するために、多くの重要な実験が行われて、総合的な観点から、真の超伝導機構が理解されたものといえる。曖昧な点があるとすると介在するフォノンの周波数であろう。今後中性子実験ならびに、電子—格子相互作用に関する計算などが行われて、フォノンに関してさらにより詳細な情報を知ることができることが期待される。


5．同位体と量子コンピューティング
　主要な元素の物性は、主に電子の数で決定されるが、核スピンに着目すると¹²C、²⁸Si、³⁰SiがI=0であるのに対して、¹³Cおよび²⁹SiはI=1/2の核スピンを有している。この核スピンは、磁場に応答してエネルギー分裂（ゼーマン効果によるエネルギー分裂）を生じる。この現象は、広く磁気共鳴に応用されている。
　核スピンが幾つか集合した全スピンの状態は、それぞれの核スピンの線形結合で表現され、その量子力学的な状態は４つの特徴を有している。１番目は、“量子力学的重ね合わせ”である。これは、シュレディンガーの猫として良く知られている状態で、量子力学的状態関数は、幾つかの状態が同時に存在している、各状態の重ね合わせとして表わすことができるというものである。２番目は、“波束の収縮”とよばれる現象で、観測した瞬間に、状態は重ね合わせの中の観測したある特定の状態に、状態関数が収縮するという特徴である。３番目は、“不確定性原理”とよばれるもので、観測量の中には一つを正確に観測しようとすれば、もう一方は不確かになる観測量が存在するというもので、運動量と位置、あるいは時間とエネルギーがそのような量である。４番目は、“量子のもつれ合い”という言葉で表現される。例えば、スピンの問題がこれにあたる。全体の状態の合成スピンが零の状態であると仮定すると、アップスピンとダウンスピンの２つのスピンの状態は完全には無関係ではなくなる。これを、量子のもつれ合いという言葉で表現する。２番目の波束の収縮と３番目の不確定性原理を組み合わせると解読が不可能な量子暗号を考え出すことができるとされ、研究が盛んに行われている。また、 1番目の量子力学的重ね合わせと４番目の量子のもつれ合いを組み合わせると、量子コンピュータの基礎概念となる。
　量子コンピューティングを達成する量子ビットとしては、電子準位、イオン準位、電子スピン、核スピンなどを考えることができる。
　この中で核スピンを適用する概念は、比較的実現可能性が高いものとして注目されている。核スピンを用いて量子コンピューティングを行う際の一つの重要な問題は、演算をする必要な時間の間、核スピンの状態を保持することができることである。これは、核スピンの緩和時間と大きく関係する。表１に示されるように、核スピンの状態が保持されている時間内（位相緩和時間T₂）の間にスピン情報を変化させて（スイッチ時間t₀）演算ができるステップ数は、T₂とt₀の比で与えられる。核スピンを用いた方法が有力であることが分かる。しかし、この重要なT₂は周りが作る局所磁場に影響を受け短くなってしまう。そこで、T₂を十分に長く保つためには、純粋な²⁹Siの列を他と分離して構成する必要がある。このように、同位体で制御された構造は、量子コンピュ−ティングの重要な候補となり得る。


表1　種々の量子ドットと総演算ステップ数







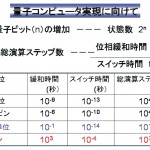
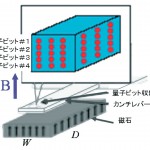
図6　全シリコン量子コンピュータ^［7］［7］T.D.Lodd, J. R. Goldman, F. Yamaguchi, Y. Yamamoto, E. Abe and K. M. Itoh : Phys. Rev. Lett. 89 (2002) 017901.


　シリコンを用いた微細加工技術は、20世紀に発展を遂げた多くの技術の蓄積がある。シリコンを基礎とした核スピン量子ドット系の量子コンピューティングは次世代の重要な研究課題と言える ^[7] ［7］T.D.Lodd, J. R. Goldman, F. Yamaguchi, Y. Yamamoto, E. Abe and K. M. Itoh : Phys. Rev. Lett. 89 (2002) 017901.。


6．おわりに
　ナノクラスタ結晶は、基礎科学としても応用研究としても様々な興味深い物性を有している。同位体元素などと組み合わせた将来の新しい研究が期待される。本研究は、文部科学省科学研究費No. 13304031 and 14076215の補助を受け、科学技術振興事業団の戦略的創造研究推進事業の一環として行われた。また、SPring-8での実験は文部科学省のナノテクノロジー総合支援プロジェクトの支援を受けて粉末結晶構造解析ビームラインBL02B2で実施された。比熱の解析に助言を頂いた東京工業大学　阿竹徹先生に感謝致します。


参考文献
［1］T. Blunier, J. Chapellaz, J. Schwander, B. Stauffer and D.Raynaud : Nature, 374 (1995) 46-49.
［2］E. J. Brook, T. Sowers, and J. Orchardo
: Science, 273 (1996) 1087-1091.
［3］J.S. Kasper, P. Hagenmuller, M. Pouchard and C. Cros : Science, 150 (1965) 1713.
［4］H. Kawaji, H. Horie, S. Yamanaka and M. Ishikawa : Phys. Rev. Lett. 74 (1995) 1427.
［5］K. Tanigaki, T. Shimizu, K. M. Itho, J. Teraoka, Y. Moritomo and S. Yamanaka : Nature Materials, 2 (2003) 653-655.
［6］V. H. Crepsi : Nature Materials 2 (2003) 650-651.
［7］T.D.Lodd, J. R. Goldman, F. Yamaguchi, Y. Yamamoto, E. Abe and K. M. Itoh : Phys. Rev. Lett. 89 (2002) 017901.




谷垣　勝己　TANIGAKI  Katsumi
大阪市立大学大学院　理学研究科　物質科学科
〒558-8585　大阪市住吉区杉本3-3-138
TEL：06-6605-2558　FAX：06-6690-5563
e-mail： tanigaki@sci.osaka-cu.ac.jp

昭和53年　横浜国立大学大学院　工学研究科　応用科学専攻　修士課程修了
横浜国立大学大学院　工学研究科　後期博士課程物質工学専攻　単位取得退学
昭和55年　日本電気株式会社　中央研究所研究員
平成１年　日本電気株式会社　基礎研究所　研究分子エレクトロニクスチームリ−ダ
平成10年　大阪市立大学大学院　理学研究科　物質科学専攻　教授　
平成16年　東北大学大学院　理学研究科　物理学専攻　教授




寺岡　淳二　TERAOKA  Junji
大阪市立大学大学院　理学研究科　物質科学専攻
〒558-8585　大阪市住吉区杉本3-3-138
TEL・FAX：06-6605-2551
e-mail : teraoka@sci.osaka-cu.ac.jp

昭和57年　大阪大学大学院　理学研究科修了
昭和59年　大阪市立大学　理学部　助手
平成５年　大阪市立大学　理学研究科　助教授




伊藤　公平　ITOH  Kohei
慶應義塾大学　理工学部　物理情報工学科
〒223-8522　横浜市港北区日吉 3-14-1
TEL：045-566-1594　FAX：045-566-1587
e-mail：kitoh@appi.keio.ac.jp

1989　慶應義塾大学　理工学部　計測工学科卒
1994　カリフォルニア大学　バークレー校　Ph. D. in Materials Science
1994　米国ローレンスバークレー国立研究所　特別研究員
1995　慶應義塾大学　理工学部就任
2003　慶應義塾大学　理工学部　助教授




清水　智子　SHIMIZU  Tomoko
Depertment of Materials Science and Engineering, University of California at Berkeley
Materials Sciences Division, Lawrence Berkeley National Laboratory, University of California
Materials Sciences Division, Mail Stop 66-201
1 Cyclotron Road, Berkeley, CA 94720 USA
TEL：+1-510-486-7478　FAX：+1-510-486-6044
e-mail：tshimizu@lbl.gov

平成15年　慶應大学卒業
平成15年　Depertment of Materials Science and Engineering, University of California at Berkeley　MS/PhDコース




守友　浩　MORITOMO  Hiroshi
名古屋大学大学院工学研究科　応用物理学専攻
名古屋市千種区不老町
TEL・FAX：052-789-4449 / 3724
e-mail：moritomo@nano.nuap.nagoya-u.ac.jp

昭和62年　東京大学　工学部　金属工学科卒業
平成１年　東京大学大学院　理学系研究科修士課程　物理学専攻修了
平成４年　東京大学大学院　理学系研究科博士課程　物理学専攻修了　理学博士
平成４年　日本学術振興会特別研究員（PD）東京大学大学院　理学系研究科
平成６年　技術研究組合オングストロームテクノロジー研究機構 研究員
平成８年　名古屋大学　理工科学総合研究センター　助教授
平成14年　名古屋大学大学院　工学研究科応用物理専攻　助教授




山中　昭司　YAMANAKA  Shoji
広島大学大学院　工学研究科
〒739-8527　東広島市鏡山1-4-1
TEL・FAX：0824-24-7740
e-mail：syamana@hiroshima-u.ac.jp

昭和44年　大阪大学　理学部　高分子学科卒業
昭和46年　大阪大学大学院　理学研究科　修士課程（高分子学専攻）修了
昭和47年　大阪府立大学　工学部　助手
昭和53年　広島大学　工学部　助教授
平成３年　同教授
平成13年　広島大学大学院　工学研究科　教授