Volume 08, No.2 Pages 95 - 102

1．研究の背景
　ガラスや液体などのいわゆる非晶質物質は、結晶性物質にはない特異な物性を示し、その工学的価値は結晶に劣らず広範囲である。そして、その物性の解明、材料としての実用化とその安全性の確立には、結晶性物質と同様に構造に基づいた物性理解が不可欠である。しかし、非晶質物質は、構造が統計的に等方性を示し、長周期性がなく、また、構造理解の基礎となる解析的な数学理論も欠如していることから、未だ構造を解析的に記述する、つまり構造を決定し表現することが困難である。これまで多くの非晶質物質の構造が、X線や中性子線、電子線を用いて研究されてきたが、ほとんどの場合、比較的解析が容易な短距離の構造（四面体、八面体などの構造ユニットあるいはクラスター構造）の解析に限られていた^{［1, 2］}［１］A. C. Wright : Adv. Struct. Res. Diffr. Meth. 5 (1974) 1.
［２］A. C. Wright and A. J. Leadbetter : Phys. Chem. Glasses, 17 (1976) 122.。しかし、非晶質物質の持つ特異性を構造的に理解するにはより高次の広範囲の構造、上記のユニットやクラスターの繋がり（中距離構造）を知ることが重要である^{［3, 4］}［３］S. R. Elliott : Nature, 354 (1991) 44.
［４］D. L. Price : Current Opinion in Solid State & Material Science, 1 (1996) 572.。
　非晶質物質の回折実験は、これまで実験室光源を用いたX線回折や中性子回折が主流であった。中性子回折の場合は、パルス中性子の出現により、高い散乱ベクトルQ（=4πsinθ/λ, 2θ：回折角, λ：入射X線の波長）まで回折データが得られることにより、規格化された回折データをフーリエ変換して得られる実空間関数の分解能を飛躍的に向上させることができるため、非晶質物質の回折実験の主流となった。一方、通常の実験室光源や従来の放射光源を用いたX線回折の場合には、低エネルギー、すなわち長波長であることから、限られた回折角で高Qには到達できず、また、高いQで散乱断面積が小さくなってしまう本質的な問題を乗り越えるだけの強度を有していないので、回折データを高いQまで精度良く測定することは困難であった。近年、SPring-8のような第三世代の放射光源や挿入光源の発達に伴い、高強度の高エネルギーX線（E≧30 keV）が利用可能となり、高エネルギーX線回折は中性子回折に匹敵する高いQまで回折データを測定できるようになった。以下に高エネルギーX線の利点を示す。
①高強度で短波長のX線であるため、比較的低角度の回折実験で、高い散乱ベクトルQまで回折データの測定が可能。
　さらに、試料による吸収や多重散乱の影響が小さく、かつ補正因子の角度依存性もほとんど無視できる。
②試料容器、高・低温装置の窓材等の吸収の影響も小さく、また、窓そのものを小さくしても広いQ 領域を測定できるため、セルに封入された試料の測定、低温、高温実験、高圧実験が容易である。また、二次元検出器等を利用した、広いQ領域の迅速測定が可能である。
③反射型の実験に比べて、低角度散乱での試料表面の影響（固体表面の粗さや液体の表面張力）を受けにくい。
④100keV以上の高エネルギーX線を利用する場合は、ほとんどの元素のK吸収端エネルギーを上回っているため、蛍光X線をディスクリミネータ、フィルター等で除去が可能。
⑤中性子に比べて、高強度であり、ビームサイズも小さいので、微少試料でも十分に統計精度の高い回折データが得られる。
　このように、高強度の高エネルギーX線を用いれば、実験室光源や従来の放射光源では得られなかった高精度の回折データを得ることができ、精密構造解析が行える。
　SPring-8では、最初の非晶質物質の高エネルギーX線回折実験は、原研ビームラインのBL14B1で行われた。偏向電磁石から水平方向に発散したビームを集光させるため、モノクロメータの第二結晶にベント機構を備えた集光光学系（サジタルフォーカスベンダー）^［5］［５］Y. Yoneda, N. Matsumoto, Y. Furukawa and T. Ishikawa : J. Synchrotron Rad., 8 (2001) 18.を用いて高強度を達成することにより実験を遂行することができた^［6］［６］K. Suzuya et al : Phys. Chem. Glasses, 41 (2000) 282.。続いて、共用ビームラインである高エネルギーX線回折ビームラインBL04B2^［7］［７］M. Isshiki, Y. Ohishi, S. Goto, K. Takeshita and T. Ishikawa : Nucl. Instr. and Meth. A, 467-468 (2001) 663.が立ち上がり、非晶質物質専用の二軸回折計^［8］［８］S. Kohara et al : Nucl. Instr. and Meth. A, 467-468 (2001) 1031.およびダイアモンドアンビルセル（DAC）を用いた高圧実験用のイメージングプレート（IP）回折計が設置された。BL04B2では既存の共用偏向電磁石ビームラインでは行われていなかった高エネルギー領域での集光光学系を組むために、水平振りの湾曲型結晶分光器を採用しており、分光結晶のブラッグ角は3°であり、下流のコンポーネントは6°に曲げて設定されている。現在使用できる分光結晶はSi 111とSi 220であり、得られるエネルギーはぞれぞれ、37.8keV, 61.7keVであるが、Si 111の場合は3次光の113.4keVも使うことができる。ビームラインの詳細は文献^{［7, 9］}［７］M. Isshiki, Y. Ohishi, S. Goto, K. Takeshita and T. Ishikawa : Nucl. Instr. and Meth. A, 467-468 (2001) 663.
［９］一色麻衣子他 : SPring-8利用者情報, Vol.5, No. 2 (2000) 94.を参照されたい。


2．BL04B2にインストールされた非晶質物質用二軸回折計
　前述のように、BL04B2には非晶質物質用二軸回折計がインストールされている。本回折計は高温融体の実験等を想定して、水平型を採用している。水平型を採用した場合には、高角度側で偏光因子による強度の減衰という欠点があるが、高エネルギーX 線を用いていることにより実験自体は低角度で行えるために、その影響はさほど大きくない。図1に二軸回折計^［8］［８］S. Kohara et al : Nucl. Instr. and Meth. A, 467-468 (2001) 1031.を示す。回折計は、通常のθ-2θおよびθ-θのステップスキャン法および二次元検出器を用いた測定を前提に設計されている。非晶質物質の回折実験を行うに当たって装置に要求される条件としては、なるべく低角度からバックグラウンドを抑えて多くのフォトンを試料に当てることである。そのために、ダイレクトビームストップの配置や検出器の遮蔽、受光スリットの組み合わせ等に工夫が施されている。通常、用いられる2θの範囲は、61.7keVの場合は0.2°〜60°、113.4keVの場合は0.1°〜35°である。




図1　SPring-8高エネルギーX線回折ビームラインBL04B2に設置された非晶質物質用二軸回折計^［8］［８］S. Kohara et al : Nucl. Instr. and Meth. A, 467-468 (2001) 1031.
A：Be窓、B：イオンチャンバー、C：真空チャンバー、D：スリット、E：2θアーム、F：Ge半導体検出器


3．酸化物ガラスの高エネルギーX線回折実験
　酸化物ガラスは、ガラスの中でも典型的なものであり、これまで多くの研究がなされてきた。とりわけ、ガラスのネットワーク構造を形成する役割を担うネットワークフォーマーガラスである、SiO₂, GeO₂, B₂O₃は回折実験のみならず、分光実験、計算機実験から多数の研究がなされてきた。にも関わらず、これらの中距離構造の違いは完全に解明されていない。そこでSPring-8 BL04B2ではこれまでこれらのガラスの高エネルギーX線回折実験を行い、パルス中性子回折のデータを併用して、逆モンテカルロ（Reverse Monte Carlo, RMC）シミュレーションからこれらの中距離構造の解明を行ってきた。
　図2にX線回折および中性回折から得られたSiO₂, GeO₂, B₂O₃の構造因子S（Q）を示す。中性子回折実験はすべてパルス中性子のデータであるが、SPring-8 BL04B2, BL14B1で測定したX線回折のデータは中性子回折並に高いQまで統計精度良く測定できていることが分かる。実験室光源や従来の放射光源から得られるX線回折実験ではQ _max=16Å^-1程度であったことを考えると、高エネルギーX線が非晶質物質の回折実験に必要不可欠であることが分かる。高いQまで回折データを測定することの最大の利点の1つはフーリエ変換した実空間関数の分解能が向上することであるが、詳細な説明は文献^{［15, 16］}［15］小原真司、鈴谷賢太郎：放射光, 14 (2001) 365.
［16］鈴谷賢太郎、小原真司：まてりあ, 41 (2002) 206.を参照されたい。
　RMCによるフィッティングの結果を図2に黒線で示す。RMCの詳細については文献^［17］［17］R. L. McGreevy and L. Pusztai : Mol. Simul., 1 (1988) 359.を参照されたい。これより、RMCの構造モデルはX線回折および中性子回折のS（Q）を広いQ範囲で再現しており、より信頼性の高い構造モデルが得られたと言える。
　SiO₂, GeO₂ガラスはSiO₄, GeO₄四面体が、B₂O₃ガラスはBO₃というOの3員環平面構造がOを共有して繋がりネットワーク構造を構成していることが知られているがその詳細は未だ完全に解明されていない。図3にRMCの構造モデルから計算された角度分布関数を示す。O-Si-O, O-Ge-Oは約109°にピークを持ち、SiO₄, GeO₄が存在していることを意味しており、RMCの構造モデルから計算された配位数が約4であることと一致している。また、O-B-O, B-O-Bは共に120°にピークを持っていること、またB-B-Bが60°にピークを持っていることから、BとOによる6員環（Bの3員環）、いわゆるボロクソールリング（図3c）を形成していることが分かる。一方、SiO₂, GeO₂ガラスの場合は、Si-O-Si, Ge-O-Geは120°よりも大きい角度にピークを持っていることから、ボロクソールリングのような対称性の良い小さいリングではなく、より大きなリングが存在していると考えられる。また、Si-Si-Si, Ge-Ge-Geの60°のピークはその強度が小さいことから、3員環の存在を表しているとその含有率は低く、その構造は図3（a）に示したものであると考えられる。さらに、Si-Si-Siの60°のピークはGe-Ge-Geのそれより小さいことから、SiO₂はGeO₂より3員環の濃度は少ないと推測される。以上の予測は、図4に示したリング分布および図5の3次元構造に反映されている。
　以上の検討より以下のようなことが明らかとなった。B₂O₃ガラスはB₃O₆というボロクソールリングと呼ばれる6員環（B, Oの3員環）平面構造の結合により中距離構造が形成されている。また、SiO₂, GeO₂ガラスは四面体がOを頂点共有することによりSi, Geの6員環（Oの6員環）が形成されていることが分かるが、その3員環の濃度はSiO₂ガラスのほうがGeO₂ガラスより少ない。SiO₂, GeO₂ガラスのリング構造の差は、Durbenら^［18］［18］D. J. Durben and G. H. Wolf : Phys. Rev. B, 43 (1991) 2355.が過去に予測しているが、本研究においてはじめて実験データに基づいたシミュレーションにより明らかになった。




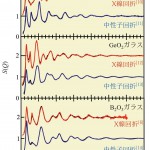
図2　SiO₂, GeO₂, B₂O₃ガラスの構造因子S（Q）
赤線：X線回折、青線：中性子回折、黒線：RMC




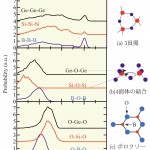
図3　RMCの構造モデルから計算されたSiO₂^［10］［10］S. Kohara and K. Suzuya : Phys. Chem. Glasses, 43C (2002) 51.，GeO₂^［12］［12］S. Kohara and K. Suzuya : Nucl. Instr. and Meth. B, 199 (2003) 23.，B₂O₃^［6］［６］K. Suzuya et al : Phys. Chem. Glasses, 41 (2000) 282.ガラスの角度分布関数と
リング構造の模式図　
赤線：SiO₂、黒線：GeO₂、青線：B₂O₃




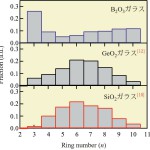
図4　RMCの構造モデルから計算されたリング分布



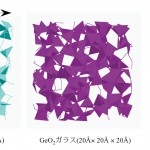
図5　RMCから得られた３次元構造



4．高温融体の高エネルギーX線回折実験
　BL04B2では高温液体の実験をめざし、高温電気炉（〜1200℃）の立ち上げ実験を行った。こういった実験は、実験室光源のX線を用いて反射法で測定するというのが一般的な方法であった。しかしながら、液体の回折パターンを測定する際、表面反射を利用する実験室光源の低エネルギーのX線を用いた場合、液体の表面張力の影響を受けるため、Qの低い領域を正確に測定することは困難である。こういった原因により生じる誤差は透過法で測定を行った中性子回折の結果との差分を取ることにより導かれる単原子液体の電子−イオン相関の研究^［19］［19］S. Takeda et al : J. Non-Cryst. Solids, 205-207 (1996) 365.を行う上で大きな障害となる。そこで、単原子液体の中でも比較的融点の低い液体Znを選んで高エネルギーX 線を用いた透過法による回折実験を試みた。
　試料容器には、円筒形の内径3φのアモルファスカーボンを用いた。Znは比較的重い原子であること、試料の回転中心からのずれ等から生じる吸収、偏光因子の補正の誤差の影響を抑えるには低角度に回折パターンを畳み込むことが有効であるという観点から、実験にはSi 111から得られる113.4keVの単色光を用いて実験を行った。測定にはアモルファスカーボンのバックグラウンド測定も含めて約8時間を要した。図6にZnの435℃における構造因子S（Q）を示す^［20］［20］小原真司他：電気化学会第69回大会講演予稿集, (2002) 309.。内側に記したS（Q）にQの重みをかけたQ［S（Q）-1］から分かるとおり、試料容器であるアモルファスカーボンのバックグラウンドの補正が完全でないものの、Q=20Å^-1まで有意のある振動が統計精度良く観測できた。また低Q側においても中性回折の結果と差分を取るに値するデータの測定が行えた。今後さらに高精度のデータを得るためには、試料容器の材質、形状、回転中心の精度の向上等、まだ解決すべき課題は多い。しかしながら、こういった問題をひとつひとつ解決することにより、これまでは決して得られなかった高精度の液体の回折情報に基づいた新しいサイエンスが期待できる。




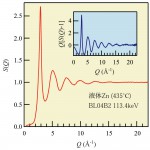
図6　液体Znの構造因子S（Q）^［20］［20］小原真司他：電気化学会第69回大会講演予稿集, (2002) 309.




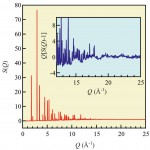
図7　Cd_0.7Zn_0.3Teの構造因子S（Q）^［22］［22］Y. Yoneda, N. Matsumoto, K. Suzuya, S. Kohara and J. Mizuki: Ferroelectrics, 268 (2002) 277.



5．結晶のPDF（Pair distirbution function）解析
　原子の配置すなわち構造を明確に定義できる結晶の場合は、非晶質物質のようにあらためて短・中距離構造を議論する必要はないように思われる。しかし、非常に興味深い物性を示す半導体混晶、誘電体、合金やゼオライトなどの多孔質物質、分子結晶などは、結晶として完全には表現しきれない構造的な乱れを内包している。そして、このような乱れ、すなわち結晶構造（以後、このBragg反射の解析から決定された結晶構造を平均結晶構造と呼ぶ）からのずれが、それらの物質特有の性質に直結している。この平均結晶構造からのずれは、散慢散乱やハロー散乱となって観測されるが、このような弱い散乱は通常のBragg反射を使った結晶構造解析ではバックグラウンドとして扱われてしまうため、解析に平均結晶構造からのずれを取り込むことができない。したがって、上記のような物質の物性の起源を明らかにするには、非晶質物質の解析と同様に、構造因子S（Q）をフーリエ変換することによって得られるPDF（Pair distribution function）において平均結晶構造からのずれである局所的な構造の乱れ（すなわち短・中距離構造）を解析すること（結晶PDF 解析^［21］［21］T. Egami : Local Structrure from Diffraction edited by S. J. L. Billinge and M. F. Thorpe, Plenum Press, New York, pp1, 1998.）が、構造物性としての結晶の構造解析には必要となってくるのである。ここでは、BL04B2における強誘電体半導体混晶Cd_0.7Zn_0.3Teの結晶PDF解析を紹介する^［22］［22］Y. Yoneda, N. Matsumoto, K. Suzuya, S. Kohara and J. Mizuki: Ferroelectrics, 268 (2002) 277.。
　CdTeおよびZnTeはイントリンシックなⅡ-Ⅵ族半導体で、pureな状態では強誘電性は示さない。ところが、これらを混ぜて混晶にすると、室温で自発分極をもつ強誘電体となる。CdTeとZnTeはともに閃亜鉛鉱構造であり、シリコンやダイアモンドの構造と類似しており、正四面体の中心が別の原子で置換された構造である。かりにCdTeとZnTeを混ぜても、結晶の平均構造に変化はなく、同じ閃亜鉛鉱構造で、対称性の低下を示すような超格子反射は現れない。閃亜鉛鉱型構造のFmの対称性のもとで、回折データに対しRietveld解析を行ったところ、非常によいフィッティング結果が得られた。この閃亜鉛鉱型の対称性Fmという構造は、強誘電性の発現が許されない対称性である。そこで、このCd_0.7Zn_0.3Te半導体混晶がもつ強誘電性発現機構を明らかにするために、平均結晶構造からのずれの情報を含むPDFの解析が必要となる。図7に回折データを規格化した構造因子S（Q）を示す。Q＞18Å^-1に非晶質物質などでみられる構造の乱れによる振動が観測されている。構造因子S（Q）をフーリエ変換したPDFを図8に黒線で示す。S（Q）を高いQまで統計精度良く測定できているため、十分な実空間分解能を持ったPDFが得られている。Rietveld解析で得られた平均結晶構造（閃亜鉛鉱構造）の原子座標を動かさずに、温度因子だけをパラメータとしてPDFにフィッティングした結果を図8に赤線で示す。閃亜鉛鉱構造（図9a）では、r＜10ÅのPDFの実験値を再現することはできていないことから、Cd_0.7Zn_0.3Te半導体混晶は平均結晶構造とは異なった短・中距離構造を持つことがわかる。次に、閃亜鉛鉱構造より原子座標をわずかに動かして、フィッティングを行った。その結果、結晶の対称性はFmより低い図9（b）のカルコパイライト構造が、短・中距離構造のモデルとして適していることが明らかになった。このカルコパイライト構造はCdとZnがTeの回りに2個ずつ配置しているため、もはやの対称性はなくなり、強誘電性の発現を許される対称性となっている。このように、強誘電体というのは、ドメインやマイクログレインの存在により平均結晶構造とは異なった局所構造を持っている可能性が非常に高い。この局所構造を、単なるローカル歪みではなく、平均結晶構造からのずれとして議論できる結晶PDF解析は、このような乱れた物質に対して有効である。




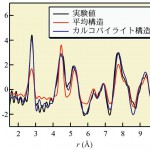
図8　Cd_0.7Zn_0.3Teの二体分布関数Ｇ（r）^［22］［22］Y. Yoneda, N. Matsumoto, K. Suzuya, S. Kohara and J. Mizuki: Ferroelectrics, 268 (2002) 277.



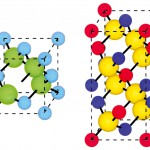
図9　PDFのフィッティング結果から得られたCd_0.7 Zn_0.3Teの局所構造モデル
（a）閃亜鉛鉱構造、（b）カルコパイライト構造



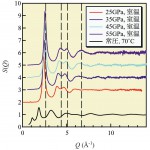
図10　高圧下におけるSnI₄の構造因子S（Q）^［23］［23］A. Ohmura, N. Hamaya, K. Sato, C. Ogawa, M. Isshiki and Y. Ohishi : J. Phys.: Condens. Matter, 14 (2002) 10553.




6．高圧下および液体のSnI₄
　このように、高エネルギーX線と集光光学系を組み合わせれば、偏向電磁石ビームラインでも微小な試料の高圧下のアモルファス状態の構造解析が可能である。
　BL04B2では、DACを用いた高圧実験用にIP回折計がインストールされている。ここでは、浜谷らにより報告されているSnI₄の高圧下でのアモルファス状態の研究^［23］［23］A. Ohmura, N. Hamaya, K. Sato, C. Ogawa, M. Isshiki and Y. Ohishi : J. Phys.: Condens. Matter, 14 (2002) 10553.について紹介する。
　X線回折実験はSnI₄が重元素から構成されている物質であること、イメージングプレートでできるだけ高いQまで回折パターンを測定するという目的から61.7keVで行われた。ビームサイズは40µm×40µmで、1つのデータを測定するのに約3時間を要した。
　図10に高圧下におけるアモルファスSnI₄の構造因子S（Q）を示す。黒線は、113.5keVのX線を用い、二軸回折計で測定した、常圧、160℃の液体のデータである。常圧の液体においては、SnI₄は分子性でSnI₄四面体というユニットを有していることが分かっている。しかしながら、高圧下のアモルファス状態ではS（Q）は常圧の液体と大きく異なっており、四面体のユニットは存在していないことが確認された。また圧力の上昇により構造に変化が起こっていることは明らかである。


7．まとめ
　SPring-8のような第三世代放射光施設では、偏向電磁石ビームラインと集光光学系を用いれば、非晶質物質の高エネルギーX線回折が、他放射光施設の挿入光源ビームラインに匹敵する高精度のデータが高いQまで測定可能である。
　しかしながら、現在行われている実験は比較的重元素を含むガラス、液体の実験が中心であるが、第三世代放射光の出現により可能となったと言われている軽元素液体の量子効果の研究（例えばD₂O/H₂Oの精密構造解析^［24］［24］P. A. Egelstaff : Phys. Chem. Liq., 40 (2002) 203.）等を行うにはやはりフラックス不足であり、こういった研究は今後挿入光源ビームラインで行う必要もある。
　BL04B2に設定されている二軸回折計は、水平型であるため、高温の融体の研究が他放射光施設に比べて容易に行えると言う利点を持つ。今後は、二次元検出器等を組み合わせつつ、不活性ガス浮上型電気炉^［25］［25］S. Krishnan and D. L. Price : J. Phys.: Condens. Matter, 12 (2000) R145.、電磁浮遊型電気炉^［25］［25］S. Krishnan and D. L. Price : J. Phys.: Condens. Matter, 12 (2000) R145.を用いた高温融体のコンテナレス測定等を行っていくことが検討されている。
　ESRFやAPSなどの他の第三世代放射光施設では、この強力な高エネルギー単色X線と2次元検出器を組み合わた透過型の回折実験によって、バルク結晶材料の非破壊観察等が盛んである^［26］［26］H. F. Poulsen et al : J. Synchrotron Rad., 4 (1997) 147.。高エネルギーX線回折は、今後材料研究における全く新しい方法として基礎と応用両面から広く受け入れられていくものと思われる。


8．謝　辞

　高エネルギーX線回折ビームラインBL04B2の設計および立ち上げに関しては、一色麻衣子氏、後藤俊治氏（JASRI）、竹下邦和氏（JASRI）、石川哲也氏（理研/JASRI）に多大なご尽力をいただきました。またテクニカルスタッフの方のご協力に感謝致します。SPring-8 BL04B2への非晶質物質用二軸回折計の設置には下村 理氏（原研）の多大なご理解、ご尽力を頂きました。
　二軸回折計、IP回折計全般の設計につきましては、㈱リガクおよびユニオン工学のスタッフの皆様にご協力頂きました。また二軸回折計の立ち上げには、坂井一郎氏（広島大学）に協力していただきました。高圧実験のデータは、浜谷 望氏、大村彩子氏（お茶大）にご提供いただきました。



参考文献
［１］A. C. Wright : Adv. Struct. Res. Diffr. Meth. 5 (1974) 1.
［２］A. C. Wright and A. J. Leadbetter : Phys. Chem. Glasses, 17 (1976) 122.
［３］S. R. Elliott : Nature, 354 (1991) 44.
［４］D. L. Price : Current Opinion in Solid State & Material Science, 1 (1996) 572.
［５］Y. Yoneda, N. Matsumoto, Y. Furukawa and T. Ishikawa : J. Synchrotron Rad., 8 (2001) 18.
［６］K. Suzuya et al : Phys. Chem. Glasses, 41 (2000) 282.
［７］M. Isshiki, Y. Ohishi, S. Goto, K. Takeshita and T. Ishikawa : Nucl. Instr. and Meth. A, 467-468 (2001) 663.
［８］S. Kohara et al : Nucl. Instr. and Meth. A, 467-468 (2001) 1031.
［９］一色麻衣子他 : SPring-8利用者情報, Vol.5, No. 2 (2000) 94.
［10］S. Kohara and K. Suzuya : Phys. Chem. Glasses, 43C (2002) 51.
［11］K. Suzuya et al : Nucl. Instr. and Meth. B, 133 (1997) 57.
［12］S. Kohara and K. Suzuya : Nucl. Instr. and Meth. B, 199 (2003) 23.
［13］C. E. Stone et al : J. Non-Cryst. Solids, 293-295 (2001) 769.
［14］A. C. Hannon et al : J. Non-Cryst. Solids 177 (1994) 299.
［15］小原真司、鈴谷賢太郎：放射光, 14 (2001) 365.
［16］鈴谷賢太郎、小原真司：まてりあ, 41 (2002) 206.
［17］R. L. McGreevy and L. Pusztai : Mol. Simul., 1 (1988) 359.
［18］D. J. Durben and G. H. Wolf : Phys. Rev. B, 43 (1991) 2355.
［19］S. Takeda et al : J. Non-Cryst. Solids, 205-207 (1996) 365.
［20］小原真司他：電気化学会第69回大会講演予稿集, (2002) 309.
［21］T. Egami : Local Structrure from Diffraction edited by S. J. L. Billinge and M. F. Thorpe, Plenum Press, New York, pp1, 1998.
［22］Y. Yoneda, N. Matsumoto, K. Suzuya, S. Kohara and J. Mizuki: Ferroelectrics, 268 (2002) 277.
［23］A. Ohmura, N. Hamaya, K. Sato, C. Ogawa, M. Isshiki and Y. Ohishi : J. Phys.: Condens. Matter, 14 (2002) 10553.
［24］P. A. Egelstaff : Phys. Chem. Liq., 40 (2002) 203.
［25］S. Krishnan and D. L. Price : J. Phys.: Condens. Matter, 12 (2000) R145.
［26］H. F. Poulsen et al : J. Synchrotron Rad., 4 (1997) 147.




小原　真司　KOHARA  Shinji
（財）高輝度光科学研究センター　放射光研究所　利用研究促進部門Ⅰ
〒679-5198　兵庫県佐用郡三日月町光都1-1-1
TEL：0791-58-2610　FAX：0791-58-2620
e-mail：kohara@spring8.or.jp


大石　泰生　OHISHI  Yasuo
（財）高輝度光科学研究センター　放射光研究所　利用研究促進部門Ⅰ
〒679-5198　兵庫県佐用郡三日月町光都1-1-1
TEL：0791-58-0831　FAX：0791-58-0830
e-mail：ohishi@spring8.or.jp


米田　安宏　YONEDA  Yasuhiro
日本原子力研究所　関西研究所　放射光科学研究センター
〒679-5148　兵庫県佐用郡三日月町光都1-1-1
TEL：0791-58-0803　FAX：0791-58-2740
e-mail：yoneda@spring8.or.jp


松本　徳真　MATSUMOTO  Norimasa
日本原子力研究所　関西研究所　放射光科学研究センター
〒679-5148　兵庫県佐用郡三日月町光都1-1-1
TEL：0791-58-2637　FAX：0791-58-2740
e-mail：matsu@spring8.or.jp


鈴谷　賢太郎　SUZUYA  Kentaro
日本原子力研究所　関西研究所　放射光科学研究センター
〒679-5148　兵庫県佐用郡三日月町光都1-1-1
TEL：0791-58-0838　FAX：0791-58-2740
e-mail：suzuya@spring8.or.jp