Volume 16, No.3 Pages 178 - 185

1．はじめに　－量子状態イメージング－

　半導体、バッテリー材料、高分子材料、生体物質など、形として認識できる全ての物は原子により構成されている。この認識は、Dēmokritosの思想的としての原子論、J. Daltonの近代原子論、そして数多くの実験による検証を経て確立された重要な科学的知識の一つである。物理学者のR. Feynmanは、その重要性について、「もし、何らかの大変動により全ての科学的知識が失われ、たったの一文しか次世代に残せなかったら、どのような一文を残すか？私は原子仮説、すなわち、全てのものは原子からできている、であると思う。なぜなら、この文には、少しの想像力と思考を働かせることによって引き出せる、自然界に関する莫大な量の情報が含まれているからである（筆者意訳）」と述べている^[1][1] R. P. Feynman, R. B. Leighton and M. Sands: Lectures on Physics (Addision-Wesley PublishingCompany, 7^th Edition, 1972) Vol.1, Chapter 1.。“少しの想像力と思考（原文：a little imagination and thinking）”と言い切るところが偉大な物理学者である。

　原子論の基本的な考え方が、物質の存在をこれ以上に分割することのできない最終的な構成要素の集まりとしてみることであるとしたならば、約1 Å（10^-8 cm）の大きさの原子は最終的な到達点ではない。原子は、さらに約5桁小さい、原子核と電子に分けることができる。複数の電子が原子核の周りにそれぞれの軌道をつくって存在し、その軌道に固有の空間的広がりが原子の大きさを決めている。原子サイズの世界では、惑星が太陽の周りを回るような古典的な軌道を考えることはできず、量子論に基づいて、電子の存在確率分布として電子の軌道を想像しなければならない。量子論で記述される状態が量子状態であり、量子状態を電子の存在確率分布として視覚的に表現することを“量子状態イメージング”とよぶことにしよう。

　前段では、暗黙の了解として位置空間の存在確率を前提としていたが、運動量空間での存在確率として量子状態を表現することもできる^[2][2] J. J. Sakurai: Modern Quantum Mechanics (Addison-Wesley Publishing Company, Revised Edition, ed. San Fu Tuan, 1994 ) Chapter 1.。例えば、ある軌道上の電子は、原子核近傍では速く、原子核から離れたところでは遅く運動し、ある一定幅の速度分布をしている。速度分布は原子核と他の電子によって作られるポテンシャルで決まるため、それぞれの軌道は特有の速度分布を示す。運動量(p)と速度(v)の関係、p = mv（m：質量）、から、速度分布は運動量分布と言い換えることができる。電子の運動量分布は、運動量空間における電子の存在確率であり、ここでは電子運動量密度とよぶことにする。ちなみに、位置空間の電子の存在確率は、電荷密度である。図1にCu 3d原子軌道(z²)の形状を示す。最大密度の1/3の密度面を描画したもので、電荷密度、電子運動量密度ともほぼ同じ形状をしている^[3][3] M. J. Cooper: Rep. Prog. Phys. 48 (1985) 415-481.（注1）。すなわち、電子運動量密度として表示することで、電荷密度と同様に、直感的に軌道をイメージすることができる。量子状態を運動量密度としてイメージングすることが本研究のテーマである。

（注1：位置空間の波動関数と運動量空間の波動関数はフーリエ変換で結ばれている。原子の波動関数は動径部と方位角部の積で与えられるが、フーリエ変換で変換されるのは動径部だけで、方位角部は位置空間、運動量空間ともに同じ形で共有されている。密度は波動関数の絶対値の2乗で与えられるので、電荷密度と電子運動量密度は同じ方位角部のため同じ形状をしている。）

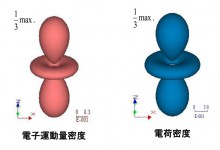
図1　Cu 3d原子軌道の一つ、z²軌道、の電子運動量密度と電荷密度。両密度とも同じ形状をしており、電子運動量密度を用いても軌道に関する直感的イメージが得られる。

　量子状態イメージングはナノテクノロジーを発展させる重要な測定技術のひとつであると考えられる。Feynmanは、原子や分子を機能を有する基本的な構成部品と見なしてナノスケールの物体を創造する技術を心に描き、1959年のアメリカ物理学会の講演でナノテクノロジーの概念を提唱した。ナノサイズの世界は量子論の物理法則が顔を出す領域であり、原子軌道や分子軌道などの量子状態を可視的に表示する量子状態イメージングは、超伝導などの量子現象に関する知識を深めるだけではなく、量子現象を動作原理とするデバイス開発において必要な測定技術になると期待される。

　本記事では、銅酸化物高温超伝導体をとりあげ、超伝導を引き起こすホール（電子が取り去られた孔）の量子状態を運動量密度として表示した研究例を紹介する。その前に、コンプトン散乱について簡単に説明したい。

2．コンプトン散乱

　コンプトン散乱は非弾性X線散乱の一つである。コンプトン散乱X線のエネルギー分布からコンプトン・プロファイルが得られる。異なる結晶方位で測定したコンプトン・プロファイルのデータセットから電子運動量密度が再構成される。このプロセスで得られた電子運動量密度を可視的に示すことが、電子の量子状態イメージングである。以下に、なぜコンプトン散乱によって電子運動量密度が得られるかについて説明しよう。

　コンプトン散乱は、Arthur H. Comptonが実験的に明らかにし、その現象に正しい解釈を与えたコンプトン効果に由来する^[4][4] A. H. Compton: Phys. Rev. 21 (1923) 483-502.。コンプトン効果は、X線が物質中の電子に当たって散乱されると、一部の散乱X線の波長が、入射X線の波長より長くなる現象である。X線を電磁波とするMaxwellの電磁気学理論では、散乱X線と入射波X線の波長は同じになる。この散乱はThomson散乱とよばれるが、X線を電磁波として考えるとコンプトン効果を説明できない。Comptonは、Einsteinの光量子仮説に基づいて、X線を一定のエネルギーと運動量を持つ粒子（光子）の集まりと考え、このX線の散乱を光子と電子の弾性衝突として取り扱うことで、コンプトン効果を説明した。以下で、光子と電子の弾性衝突を考えよう。

　波長λのX線の場合、光子のエネルギーはħω = ħ (2 πc/λ)、運動量はħk = ħ (2 π/λ)eで与えられる。ここで、cは光速、eはX線の進行方向の単位ベクトルである。散乱前と後について、光子のエネルギーをħω₁とħω₂、光子の運動量をħk₁とħk₂、電子のエネルギーをE₁とE₂、電子の運動量をp₁とp₂とおく（図2）と、エネルギー保存則と運動量保存則より

ħω₁ + E₁ = ħω₂ + E₂,　　　　　　　　(1)

ħk₁ + p₁ = ħk₂ + p₂,　　　　　　　　 (2)

を得る。また、電子のエネルギーを運動エネルギーとポテンシャル・エネルギーに分け、

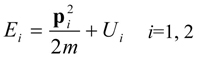　　　　　(3)

とおく。ポテンシャル・エネルギーU_iはコンプトン散乱に関与する電子以外の全ての電子と全ての原子核によってつくられたポテンシャルである。弾性衝突で電子が弾き飛ばされた後に、飛ばされた電子1個分の孔を埋め合わせるように周囲の電子群が緩和し、この緩和に伴いポテンシャルU₂が時間的に変化する。しかし、光子と電子の衝突は瞬時に起こるため、電子群の緩和が起こりポテンシャルが変化する前に衝突現象は終了するとして、

U₁ = U₂ 　　　　　　　　　　　　　 (4)

とおく。これをインパルス近似という。以上の(1)〜(4)から、散乱後の光子のエネルギーħω₂を導くと、

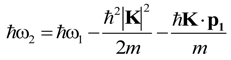　　　(5)

となる。ここで、K ( = k₁ - k₂) は散乱ベクトルである。通常の実験条件では、入射X線エネルギー（すなわち、散乱前の光子のエネルギーħω₁）と散乱角θ（すなわち、散乱ベクトルK）は一定値に設定されているので、第1項と第2項は定数になる。ところが、第3項には、散乱前の電子の運動量と散乱ベクトルの内積K・p₁が含まれているため、1散乱イベントにおける散乱X線のエネルギーħω₂は電子の運動量p₁の散乱ベクトルKへの射影成分に依存する。物質中にはアボガドロ数程度（〜10²³個）の電子がそれぞれの速度（すなわち運動量）で運動しているので、繰り返し測定をして得られたコンプトン散乱X線のエネルギー・スペクトルI (ħω₂) は、電子の運動量分布に対応して幅広になる（図3）。ここで、電子運動量密度n(p) = n(p_x, p_y, p_z) とおき、p_z軸を散乱ベクトルKと平行におくと、

I (ħω₂) ∝ J (p_z) = ∫∫n(p)dp_xdp_y 　　　　(6)

となる。ここで、p = (p_x, p_y, p_z) は運動量座標で、J(p_z) はコンプトン・プロファイルである。I(ħω₂)から J(p_z) へは確立された補正等によって直接的に変換される。

　量子状態イメージングには、電子運動量密度n(p)が必要である。電子運動量密度は、異なる結晶方位で測定したコンプトン・プロファイルのデータ・セットから、数値計算的に再構成する。本研究では、直接フーリエ法^[5,6][5] R. Suzuki, M. Osawa, S. Tanigawa, M. Matsumoto and N. Shiotani: J. Phys. Soc. Jpn. 58 (1989) 3251.
[6] Y. Tanaka et al.: Phys. Rev. B 63 (2001) 045120.を用いているが、説明は紙面の都合で省略する。

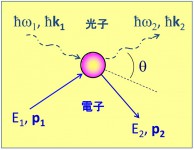
図2　コンプトン散乱の概念図。コンプトン散乱は光子と電子の弾性衝突である。

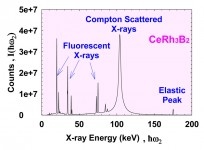
図3　175 keVの入射X線、散乱角178°で測定したX線のエネルギー・スペクトル。103 keVの幅広なラインがコンプトン散乱X線。その他、蛍光X線やThomson散乱X線（175 keV）が検出されている。

3．銅酸化物高温超伝導体への応用例：ホール状態イメージング

　超伝導は謎に満ちた自然現象のひとつで、物質を冷やしたときにある温度（超伝導転移温度）で電気抵抗が消失する現象である。超伝導は1911年にヘイケ・カメルリング・オネスによって水銀において発見され、本年はちょうど100周年にあたる。1986年に発見された銅酸化物高温超伝導体は約30 K（ケルビン）とそれまで合金系超伝導体Nb₃Geの23 Kを大きく超える超伝導転移温度を示し、その後の材料開発の進展により、135 Kの超伝導転移温度を示す銅酸化物高温超伝導体が見つかっている。合金系超伝導体の場合、その超伝導機構は自由に動ける電子と格子振動の相互作用を基礎にしたBardeen-Cooper-Schrieffer (BCS)理論でうまく説明できるが、この従来のBCS理論では100 Kを超える超伝導転移温度を説明することは難しいとされ、銅酸化物高温超伝導体は合金系超伝導体とは異なる機構で超伝導になると考えられている。

　銅酸化物高温超伝導体の謎のひとつは、相図上に現れるドーム状をした超伝導領域である。その相図を図4に示す。今回測定した超伝導体La_2-xSr_xCuO₄（LSCO）は、絶縁体のLa₂CuO₄にLaをSrで置換することによって超伝導になる。Laは3個、Srは2個の価電子を持っているので、LaをSrで置換すると物質中の価電子数が減少する。これは正電荷を持った孔（正孔：ホール）を超伝導物質にドープすることと同じなので、Sr置換のことをホール・ドープとよぶ。図4にあるように、ホール・ドープ量と超伝導転移温度の関係はドーム形状をし、37 Kの最高転移温度を示す最適ドープ量x = 0.15を境にして、x < 0.15の領域をアンダー・ドープ領域、x > 0.15の領域をオーバー・ドープ領域とよぶ。なぜ、超伝導領域がドーム形状をし、最適ドープを越えたオーバー・ドープ領域で超伝導転移温度が下がり、超伝導が消滅してしまうのかは、銅酸化物高温超伝導体の謎の一つとされている。このドープ形状を説明できる量子状態モデルの構築が高温超伝導機構を理解する上で不可欠であることは言うまでもない。

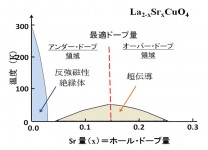
図4　銅酸化物高温超伝導体La_2-xSr_xCuO₄の相図（横軸：Sr濃度（ホール・ドープ量）；縦軸：温度）。銅酸化物高温超伝導体には最適なホール・ドープ量が存在し、そのドープ量（x = 0.15）までは超伝導転移温度が上昇し続けるが、それ以上のドープは逆効果となり、超伝導転移温度が減少していく。このドーム形状をした超伝導転移温度変化は銅酸化物高温超伝導体の謎のひとつと言われている。

　銅酸化物高温超伝導体の電子構造はどのようになっているのだろうか。その前に、図5にLSCOの原子構造を示す。[001]に長い単位胞であるが、体心位置と8つの隅に、1個のCu原子と6個のO原子からなる八面体構造（図6）がある。この八面体のCu 3d軌道とO 2p軌道からなる状態がフェルミ準位近傍にあり、超伝導に関係していると考えられている。図7にその電子状態を簡略に示す。Cu 3d軌道は上下に分裂し、その分裂したCu 3d軌道状態の間にO 2p軌道から成る状態（O 2pバンドとよぶ）が位置している。上に分裂したCu 3d軌道状態には電子は無く、下の状態は電子が詰まっている。x = 0のLa₂CuO₄では、O 2pバンドは電子で詰まっているため、電子が自由に動けずに絶縁体である。Sr置換によるホール・ドープすると、ホールは八面体の水平面内にあるO 2p軌道に入る。その結果、図7のようにO 2pバンドの上端に電子が抜けた状態ができ、電子が動ける金属になる。アンダー・ドープ領域から最適ドープ領域にかけて、O 2p軌道（バンド）に入ったホールが超伝導を引き起こすことがわかっているが、超伝導転移温度が降下し最終的には超伝導状態が消失するオーバー・ドープ領域ではどうなっているのかは未解明のままである。X線吸収測定の結果^[7][7] D. C. Peets et al.: Phys. Rev. Lett. 103 (2009) 7942.は、オーバー・ドープ領域でホールはO 2p軌道に入らないことを示唆している。

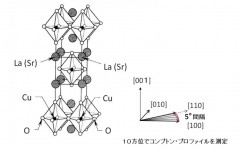
図5　銅酸化物高温超伝導体La_2-xSr_xCuO₄の結晶構造とコンプトン散乱測定をした結晶方位

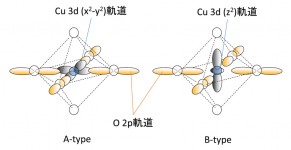
図6　八面体構造内のO 2p軌道とCu 3d軌道。Cu 3d軌道は（x²-y²）と（z²）の2種類がある。アンダー・ドープ領域ではホールはO 2p軌道に入るが、オーバー・ドープ領域ではCu 3d軌道に入る。

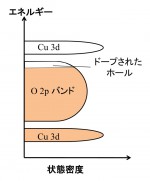
図7　電子状態密度の概略図。Cu 3d軌道は上下に分裂し、その分裂したCu 3d状態の間にO 2pバンドが位置している。アンダー・ドープ領域では、ドープしたホールはO 2pバンドの上端に入る。

　コンプトン散乱測定は高エネルギー非弾性散乱ビームライン（BL08W）に設置されたCauchois型X線スペクトロメータを用いて行われた。115 keVの高エネルギーX線を用いるため、試料表面の影響を受けることなく、バルク状態を測定できる。LSCO(x = 0.0, 0.08, 0.15, 0.30)のそれぞれの単結晶試料について、[100]と[110]の間を5度間隔で分割した計10方位のコンプトン・プロファイルを測定し、直接フーリエ法によって、[001]に沿って電子運動量密度n(p) を射影積分した2次元電子運動量密度分布を実験的に求めた。LSCOは2次元性の強い物質のため、[001]に沿って射影積分しても電子構造の特徴は失われない。ホール・ドープ量(x)が異なる2つの電子運動量密度分布の差をとることで、ホールの運動量密度分布を求めた。図8にアンダー・ドープ領域（(x = 0.0) - (x = 0.15)）とオーバー・ドープ領域（(x = 0.15) - (x = 0.30)）におけるホール運動量密度分布を示す^[8][8] Y. Sakurai et al.: Science 332 (2011) 698-702.。アンダー・ドープ領域とオーバー・ドープ領域で分布が異なり、両領域間でホール状態が異なることを示している。また、その違いは、2つのタイプ（A-typeとB-type）（図9）として観測された。A-typeは[100]/[010]方向、B-typeは[110]方向に沿って現れる運動量分布を与える。

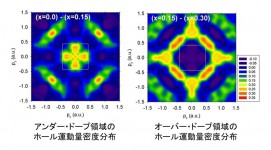
図8　ホール運動量密度分布（実験結果）。アンダー・ドープ領域とオーバー・ドープ領域で大きく異なることがわかる。この実験事実はそれぞれの領域でドープされたホールの状態が異なっていることを示している。赤色、黄色の部分にホールが多数存在していることを表している。四角い白枠は第1ブリルアン・ゾーンを表す。

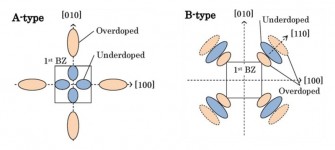
図9　アンダー・ドープ領域とオーバー・ドープ領域のホール運動量密度変化の模式図。A-typeとB-typeの2種類がある。

　図8のホール運動量密度分布に見られる2つのタイプ、すなわちA-typeとB-typeは2つの分子軌道でおおよそ説明できる。この2つの分子軌道を図10のAとDに示す。第1原理計算によるバンド描像からも、この2つの状態の寄与が示唆されている^[8][8] Y. Sakurai et al.: Science 332 (2011) 698-702.。図10Aは、2つのO 2p_xと2つのO 2p_yからなるZhang-Rice状態^[9][9] F. C. Zhang and T. M. Rice: Phys. Rev. B 37 (1988) 3759-3761.とCu 3d x²-y²で作られる分子軌道（A-typeに対応）、図10Dは、2つのO 2p_xと2つのO 2p_yからなるNode-less状態とCu 3d z²で作られる分子軌道（B-typeに対応）である。Zhang-Rice状態とNode-less状態の違いは、O 2p軌道の位相（＋,－）にある。図10BはZhang-Rice状態のみ、図10CはZhang-Rice状態とCu 3d x²-y²軌道の混成状態の運動量密度分布を示し、図10EはNode-less状態のみ、図10FはNode-less状態とCu 3d z²軌道の混成状態の運動量密度を示している。両分子軌道とも、Cu 3d軌道との混成により外側（運動量の大きな方向）へ重みが移行し、図8（実験結果）のアンダー・ドープ領域からオーバー・ドープ領域への変化を再現している。すなわち、アンダー・ドープ領域でホールはO 2p軌道に入るが、オーバー・ドープ領域ではCu 3d軌道に入ることを示している。

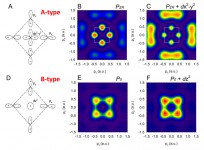
図10　八面体構造内のCu-Oの分子軌道と運動量密度分布。詳細は本文参照。

　分子軌道計算は実験結果の全体的な特徴を説明しているが、構造の詳細を再現できていない。また、詳しく述べなかったが第1原理バンド理論計算の結果も同様である。この理由は両者それぞれの理論計算において用いられている計算近似に限界があるためである。すなわち、分子軌道計算では、5つの原子（Cu 1個とO 4個）の軌道のみからLSCOのホール・ドープによる電子構造変化を再現しようとし、第1原理バンド計算では、結晶全体の原子を考慮するものの電子相関効果が適切に取り込まれていない。実験結果を詳細に説明するには、より現実に近いモデルに立った計算手法、例えば、バンド理論計算にZhang-Rice1重項^[9][9] F. C. Zhang and T. M. Rice: Phys. Rev. B 37 (1988) 3759-3761.の形成を電子相関効果として取り込む手法の開発が必要である。また、Jahn-Teller歪の影響やポーラロン・モデルの検討が今後の課題として残っている。将来の理論モデル計算の発展に期待したい。

4．コンプトン散乱による量子状態イメージングのバリエーション

　銅酸化物高温超伝導体のホール状態イメージングを例として取り上げ、コンプトン散乱による量子状態イメージングについて説明してきた。この研究例では、ホールの軌道状態を運動量密度分布上に可視化している。コンプトン散乱では、運動量密度分布の他に、k空間電子占有数密度分布やr空間波動関数自己相関分布を用いて、量子状態イメージングが可能である。以下に、この2つについて簡単に説明して、本記事を結びたい。

（1）k空間電子占有数密度分布による量子状態イメージング

電子の波数ベクトルkと運動量ベクトルpは、p = k + G_iの関係にある。ここで、G_iはi番目の逆格子ベクトルである。あるkについて、G_iで結ばれるすべてのp点の電子運動量密度n(p)を足し合わせて得られるk空間の密度分布がk空間電子占有数密度分布N(k) である：

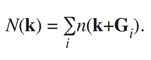　　　　　　　(7)

フェルミ面はk空間における電子占有と非占有の境界面として定義されるので、N(k)からフェルミ面形状を可視化することができる^[10,11,12][10] D. G. Lock, V. H. C. Crisp and R. N. West: J. Phys. F: Met. Phys. 3 (1972) 561-570.
[11] S. B. Dugdale et al.: Phys. Rev. Lett. 96 (2006) 046406.
[12] A. Koizumi et al.: Phys. Rev. Lett. 106 (2011) 136401.。

（2）r空間波動関数自己相関分布による量子状態イメージング

r空間波動関数自己相関分布は電子運動量密度n(p)の3次元フーリエ変換で得られる^[13][13] W. Weyrich, P. Pattison and B. G. Williams: Chem. Phys. 41 (1979) 271-284.。r空間は位置空間のことである。1電子波動関数に対する“電子密度関数”の一つで、一般にB(r)関数とよばれる。電荷密度や電子運動量密度も“電子密度関数”のひとつである。B(r)関数は、ブロッホの定理のもと、位置空間における波動関数の自己相関を与えるので、波動関数のコヒーレンス分布を可視化できる可能性がある。応用例はほとんどなく、今後の研究開発課題の一つである。

5．謝辞

　本原稿の執筆にあたって、小泉昭久准教授から有益なコメントを頂いた。銅酸化物高温超伝導体の研究は、伊藤真義博士、B. Barniellini博士、P. E. Mijnarends教授、R. S. Markiewicz教授、S. Kaprzyk教授、J.-M. Gillet教授、脇本秀一博士、藤田全基准教授、S. Basak女史、Yung Jui Wang氏、W. Al-Sawai博士、H. Lin博士、A. Bansil教授、山田和芳教授との共同研究として行われた。コンプトン散乱実験はSPring-8、BL08Wで行われた（課題番号：2003B0762、2004A0152、2007B1413、2008A1191、2010A1907）。

参考文献

[1] R. P. Feynman, R. B. Leighton and M. Sands: Lectures on Physics (Addision-Wesley Publishing Company, 7^th Edition, 1972) Vol.1, Chapter 1.

[2] J. J. Sakurai: Modern Quantum Mechanics (Addison-Wesley Publishing Company, Revised Edition, ed. San Fu Tuan, 1994 ) Chapter 1.

[3] M. J. Cooper: Rep. Prog. Phys. 48 (1985) 415-481.

[4] A. H. Compton: Phys. Rev. 21 (1923) 483-502.

[5] R. Suzuki, M. Osawa, S. Tanigawa, M. Matsumoto and N. Shiotani: J. Phys. Soc. Jpn. 58 (1989) 3251.

[6] Y. Tanaka et al.: Phys. Rev. B 63 (2001) 045120.

[7] D. C. Peets et al.: Phys. Rev. Lett. 103 (2009) 7942.

[8] Y. Sakurai et al.: Science 332 (2011) 698-702.

[9] F. C. Zhang and T. M. Rice: Phys. Rev. B 37 (1988) 3759-3761.

[10] D. G. Lock, V. H. C. Crisp and R. N. West: J. Phys. F: Met. Phys. 3 (1972) 561-570.

[11] S. B. Dugdale et al.: Phys. Rev. Lett. 96 (2006) 046406.

[12] A. Koizumi et al.: Phys. Rev. Lett. 106 (2011) 136401.

[13] W. Weyrich, P. Pattison and B. G. Williams: Chem. Phys. 41 (1979) 271-284.

櫻井　吉晴　SAKURAI Yoshiharu

（財）高輝度光科学研究センター　利用研究促進部門

〒679-5198　兵庫県佐用郡佐用町光都1-1-1

TEL：0791-58-2750

e-mail：sakurai@spring8.or.jp