Volume 06, No.5 Pages 383-389

1．はじめに
　ペロフスカイト型Mn酸化物は、巨大磁気抵抗効果（CMR）の発見以来、そのメカニズムの解明や応用上の観点から活発に研究が行われている物質である。この物質は、1950年代から実験・理論の両面で精力的に研究されている。ホールドープによる強磁性と金属的な電気伝導の出現機構については、二重交換相互作用（DE）により説明されてきた^［1−3］［1］C. Zener：Phys. Rev. 82（1951）403.
［2］P. W. Anderson and H. Hasegawa：Phys. Rev. 100（1955）675.
［3］P. -G. de Gennes：Phys. Rev. 118（1960）141.。しかし、スピンの自由度のみを考慮したDE機構では、CMR効果を含む伝導現象や、ホールドープや温度変化にともなう複雑な磁気構造の変化等、多くの実験結果を説明しきれていない。そのため、最近では、電荷やスピンの自由度だけでなく、軌道の自由度の重要性が取り上げられるようになった。
　どのような軌道が問題となるのか、ペロフスカイト型Mn酸化物の構造的な特徴であるMnO₆八面体を考えてみよう。ホールドープされていない場合には、中心に位置するMn³⁺イオンが、6個の酸素イオンによって囲まれている。従って、Mn³⁺イオンの3d軌道状態は、酸素イオンによる結晶場のため、3重縮退したt_2ｇ軌道（d_xy, d_yz, d_zx）と、2重縮退したe_g軌道（d_x²−_y², d3_z²−_r²）に分裂している。ここで、4つの3d電子をフントの規則に従って詰めてゆくと、t_2ｇ軌道に3つ、e_g軌道に1つ入った高スピン状態をとる。t_2ｇ軌道は、酸素イオンを避けた方向に伸びており、局在性が強いが、e_g軌道は、酸素イオンの方向に伸びており、その2p軌道と強く混成していると考えられる。ただし、Mn³⁺イオンのみの場合、各Mnサイトに1つずつのe_g電子が存在することになり、強い電子相関によって絶縁体的状態となっている。ここにホールをドープすると、そのホールはe_g軌道に入るものと考えられ、Mnイオンの一部はMn⁴⁺になる。この時e_g電子はMn⁴⁺サイトへの跳び移りが可能となるが、t_2ｇスピンとの間に強いフント結合が働いているため、遷移確率は跳び移った先のt_2ｇスピンの向きに依存する。系全体として運動エネルギーの利得を得るため、e_g電子が各Mnサイトのスピンを揃えるように回ることになり、強磁性金属状態が出現する。これが、前述のDE機構である。
　Mn³⁺イオンの場合、MnO₆八面体のヤーン・テラー（J-T）歪みによってe_g軌道の縮退がとけて2つの軌道に分かれる場合がある。J-T歪みと軌道自由度は密接に関係しており^{［4, 5］}［4］A. J. Millis et al.：Phys. Rev. Lett. 74（1995）5144.
［5］H. Koizumi et al.：Phys. Rev. Lett. 80（1998）4518.、Mn³⁺とMn⁴⁺が混じった現実の系において、どちらのe_g軌道に電子が入るか、さらにはどの様な軌道配列をとるかが電気伝導性や磁気秩序に大きく影響すると考えられる。従って、e_g軌道の状態を、スピンなどと同様に直接的に調べることができる実験的手法が望まれている。その一例として、最近、共鳴X線散乱による測定が精力的に行われている。この手法は、軌道秩序による電子状態の空間的変調を、Mn-K吸収端のエネルギーを持つX線を利用して調べる方法である。その散乱強度は、回折X線の偏光状態と、散乱ベクトル回りの試料の回転角に依存して大きく変化する。この手法により、ペロフスカイト型Mn酸化物において初めて、Mn³⁺とMn⁴⁺が周期的に配列した電荷秩序状態と共に、反強的な軌道秩序状態が観測されている^［6−9］［6］Y. Murakami et al.：Phys. Rev. Lett. 80（1998）1932.
［7］Y. Murakami et al.：Phys. Rev. Lett. 81（1998）582.
［8］S. Ishihara et al.：Phys. Rev. Lett. 80（1998）3799.
［9］S. Ishihara et al.：Phys. Rev. B 58（1998）13442.。
　我々は、これに相補的な測定手段として、円偏光の高エネルギー放射光X線を用いた磁気コンプトン散乱の測定によるMn酸化物の軌道状態の研究を行っている。磁気コンプトン散乱の特徴を利用すると、強磁性相における、2つのe_g軌道に対する占有率を、区別して求めることができるのである。以下では、その具体的な説明を行い、現在までの結果を紹介したい^［10］［10］A. Koizumi et al.：Phys. Rev. Lett. 86（2001）5589.。


2．実験
2-1．磁気コンプトン散乱の特徴
　コンプトン散乱は、X線と電子の粒子的な衝突によって起こる。この時、エネルギーと運動量の保存則が成り立ち、試料が固体の場合には固体内電子の運動量分布についての情報を得ることができる。入射X線に円偏光を用いると、磁性体内の磁性電子のみの運動量分布やスピン磁気モーメントを測定することができ、磁気コンプトン散乱と呼ばれている^［11］［11］N. Sakai：J. Appl. Cryst. 29（1996）81.。実際には、円偏光の向きを固定し、試料の磁化を反転させた時の散乱強度の差から磁気効果を得る。入射X線のエネルギーが電子の束縛エネルギーよりもずっと高い場合には、インパルス近似を適用でき^［12］［12］P. Eisenberger and P. M. Platzman：Phys. Rev. A 2（1970）415.、磁気効果も含めたコンプトン散乱の微分散乱断面積は、

（1）

のように与えられる。ここで、ωは散乱光子のエネルギー、Ωは、散乱の立体角である。また、Aで表した係数は主に電荷による散乱行列要素、Bは磁化方向に沿ったスピンによる散乱行列要素である。J（p_z）、J_mag（p_z）は、コンプトンプロファイルと磁気コンプトンプロファイル（MCP）を表し、それぞれ、
（2）

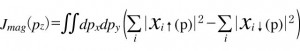（3）

のように記述される。p_zは散乱ベクトル方向の電子の運動量成分を表し、χ_iσ（p）は実空間の波動関数φ_iσ（r）をフーリエ変換した運動量表示の波動関数である。添え字i、σは、電子状態、スピンを区別するために付けられている。（3）式は、MCPが上向きスピンと下向きスピンの差、即ち、磁性電子の運動量分布を与えることを示しているが、MCP測定はスピン磁気モーメントによる散乱のみを観測するもので、軌道磁気モーメントは観測しない。
　MCP測定には、軌道研究という観点からみて非常に有効な特徴がある。コンプトンプロファイルは、軌道ごとに異なる形を示すのである。また、同じ軌道であっても、観測する方向によって、プロファイルが異なる。孤立原子におけるt_2ｇ軌道 及びe_g軌道について、この様子を図1に示す。d_x²−_y²軌道とd3_z²−_r²軌道で、全く異なるプロファイルを示すことがお分り頂けるであろう。（この特徴は、電子が占有している軌道の波動関数に由来するもので、軌道磁気モーメントの有無には関係ないことに注意されたい。）解析において、この特徴を用いれば、2つのe_g軌道（d_x²−_y² d3_z²−_r²）とt_2ｇ軌道の占有数を区別して求めることが可能なのである。また、プロファイルの幅は波動関数の空間的な広がりを反映するので、観測される電子の局在性・遍歴性についての情報を得られるものと期待できる。従って、Mn酸化物においては、Mn 3d軌道とO 2p軌道の混成状態がMCPに反映されるであろう。Mn酸化物の磁化がMn 3d軌道を占有している電子のスピンに由来していること、また、電気伝導においても磁性電子が深く関与していることを考えると、MCP測定は、この系を研究するのに有効な手法の一つであるといえる。



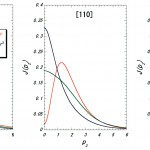
図1　各軌道のコンプトンプロファイル
赤線：x²−y²軌道、青線：3z²−r²軌道、緑線：t_2g軌道。いずれも原子軌道のプロファイルで、t_2g軌道については、xy、yz、zxの各軌道の和で示している。横軸p_zは原子単位［a.u.］である。


2-2．試料
　測定に用いた試料は、La_2-2xSr_1+2xMn₂O₇（x＝0.35, 0.42）の単結晶で、フローティングゾーン法で作製されている。結晶構造を図2に示す。MnO₂面が2枚積層したブロック層と（La, Sr）₂O₂ブロック層が交互に積み重なっており、2次元性の強い物質である。層状物質を測定対象とした理由の一つは、質の良い大きな単結晶が作製可能なことである。Mn酸化物は、試料作製時に他の方向を向いたドメインが混入しやすいが、このようなドメインが存在すると軌道状態を区別することが困難になる。もう一つの理由としては、MnO₂面内のバックリングが小さいことである。Mn-O-Mnが直線的に並んでいると見なせるならば、t_2g軌道とe_g軌道は混成していないとして、それぞれの軌道を別々に扱うことが許されるからである。



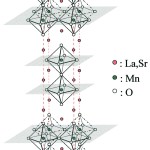
図2　La_2-2xSr_1+2xMn₂O₇の結晶構造

　La_2-2xSr_1+2xMn₂O₇は、典型的なCMR物質であるLa_1-xSr_xMnO₃より更に大きなCMR効果を示すことから興味を持たれており、この系の構造、磁性、伝導性について、既にたくさんの研究が行われている^{［13−27］}［13］Y. Moritomo et al.：Nature 380（1996）141.
［14］J. F. Mitchel et al.：Phys. Rev. Lett. 55（1997）63.
［15］D. N. Argyriou et al.：Phys. Rev. Lett. 78（1997）1568.
［16］D. N. Argyriou et al.：Phys. Rev. B 55（1997）R11965.
［17］K. Hirota et al.：J. Phys. Soc. Jpn. 67（1998）3380.
［18］D. S. Dessau et al.：Phys. Rev. Lett. 81（1998）192.
［19］T. Okuda et al.：Phys. Rev. B 60（1999）3370.
［20］K. Hirota et al.：J. Phys. Soc. Jpn. 68（1999）1463.
［21］M. Kubota et al.：J. Phys. Soc. Jpn. 68（1999）2202.
［22］M. Kubota et al.：J. Phys. Chem. Solids 60（1999）1161.
［23］H. Fujioka et al.：J. Phys. Chem. Solids 60（1999）1165.
［24］T. Ishikawa et al.：Phys. Rev. B 62（2000）12354.
［25］Q. Li et al.：Phys. Rev. B 63（2000）024417.
［26］M. Kubota et al.：J. Phys. Soc. Jpn. 69（2000）1606.
［27］M. Kubota et al.：J. Phys. Soc. Jpn. 69（2000）1986.。軌道状態についての研究の一例としては、中性子回折実験による磁気構造、J−T歪み、格子定数などのホール濃度（x）依存性の測定が挙げられる^［22］［22］M. Kubota et al.：J. Phys. Chem. Solids 60（1999）1161.。それによると、0.3＜x＜0.32の領域では、低温で、磁化容易軸がc軸方向を向いた強磁性金属状態（FM−Ⅱ）であり、x〜0.32付近で磁化容易軸が急激に変化し、0.32＜x＜0.38の領域では、ab面内に磁化の揃った強磁性金属状態（FM−Ⅰ）になる。更にホール濃度の高い0.39＜x＜0.48では、2層のMnO₂面間で磁化の向きが角度をなすキャント反強磁性金属状態（FM−Ⅰ+AFM−Ⅰ）になり、x〜0.48以上では、キャント角が180度に達し反強磁性の絶縁体状態（AFM−Ⅰ）となる。また、ホール濃度の増加に伴ってJ−T歪みが減少してゆく。磁気構造とJ−T歪みのホール濃度依存性の比較から、低ホール濃度領域ではd3_z²−_r²軌道が支配的であり、ホール濃度が増加するにつれてd_x²−_y²軌道が支配的な状態へと変化してゆくことが示唆されている。


2-3．BL08Wにおける測定
　MCP測定は、BL08WのAハッチで行った。ここには、挿入光源として楕円マルチポールウイグラーが設置されており、高エネルギーの円偏光X線が得られるSPring−8で唯一のビームラインである。図3の実験配置図に示すように、271keVに分光した円偏光X線を試料に入射し、後方にコンプトン散乱されてきたX線を、10素子のSSDで検出する。試料は、冷凍機に取り付けられ、更に、超伝導マグネットのボア内に挿入される。測定時の温度は10Kで、試料の磁化を反転させるため、±2.5Tの磁場を試料の［001］軸方向に交互に印加した。それぞれの磁場方向で測定した散乱強度の差からMCPが得られるのであるが、SSDの各素子で得られたデータを足し合せる前に、素子毎に、試料の吸収と散乱断面積に対する補正を行っている。図4と5に、x＝0.35とx=0.42の各試料で得られたMCPを示す。以下で述べる解析上の比較のため、各図において左右に2つのパネルを示しているが、●で表されているデータは同一のものである。MCPの面積は、それぞれ、ホール濃度から見積もられた3d電子数で規格化されている。横軸pzのZ軸は、単結晶試料の［001］軸方向に平行である。




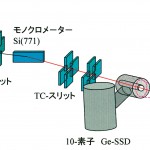
図3　磁気コンプトン散乱の模式的な実験配置図
FEスリットで切られた白色X線は、モノクロメーターで単色化されると同時に、左右方向について集光される。TCスリットで整形された単色X線は、試料上で3㎜×1㎜のスポットになる。散乱角178°の散乱X線が、Ge-SSDで分光される。




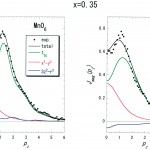
図4　x＝0.35の試料で得られたMCPとフィッティング解析の結果
左パネルは、クラスター計算から求めたプロファイルによる解析。右パネルは、Mn^4＋の孤立イオンに対するプロファイルによる解析。●：実験データ、黒線：フィッティング曲線、緑線：t_2g軌道の成分、赤線：e_x²−_y²軌道の成分、青線：e3_z²−_r²の成分。




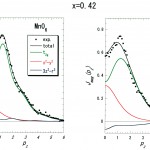
図5　x＝0.42の試料で得られたMCPとフィッティング解析の結果
左右のパネルについては、図4に同じ。


3．クラスター計算を用いた解析と結果
　前節で述べた特徴を用いた解析とは、具体的には、各軌道のプロファイルを実験データにフィットし、その面積から軌道占有数を求めるということである。そのためには、予め、軌道毎のプロファイルを求めておかなければならない。軌道という言葉からは、まず、アトミックな軌道を想像してしまうが、後で分るように、このような軌道では、MCPを説明できず、実際にはMn 3d軌道とO 2p軌道の混成を考慮する必要があった。そこで、我々は、（MnO₆）⁸⁻クラスターに対する分子軌道計算を行うことにより各軌道の波動関数を求め、それを基に導出したプロファイルを用いて、フィッティング解析を行った。分子軌道計算にあたっては、マーデルングポテンシャルとして、クラスターの周りに444の点電荷を配置し、Mn、O、Sr、Laに対し、それぞれ、+3、−2、+2、+3の価数を想定した。ただし、LaとSrについては、それらが一様に分布しているものとし、各原子位置での価数を、平均値：+8/3（x＝0の時の値）で置き換えた。また、構造パラメーターとして、x=0.35の試料のT=10Kでの値を基にし^［26］［26］M. Kubota et al.：J. Phys. Soc. Jpn. 69（2000）1606.、酸素のバックリングを無視した結晶構造を想定した。このようなモデルのもとで、クラスター内のスピンをSz＝3/2として、GAMESSプログラムにより、restricted Hartree-Fock（RHF）計算を行った^{［28, 29］}［28］M. W. Schmidt et al.：J. Comput. Chem. 14（1993）1347.
［29］A. Schäfer et al.：J. Chem. Phys. 100（1994）5829.。また、比較のため、孤立したMn⁴⁺イオンについても同様なRHF計算を行い、アトミックなプロファイルも求めている。
　フィッティング解析の結果を説明する前に、［001］軸方向について計算されたt_2ｇ軌道とe_g軌道のプロファイルが、クラスターモデルと孤立イオンの場合で、どの程度異なっているかを見てみよう。図6に各軌道のプロファイルを示す。クラスターモデルの結果を赤線で、孤立イオンの結果を黒線で示している。t_2ｇ軌道については、d_xy、d_yz、d_zxの各軌道の和で、e_g軌道については、2つの軌道を区別し、e_x²−_y²、e3_z²−_r²と表した。いずれのプロファイルも、実験の運動量分解能：FWHM=0.47 a.u. でコンボリューションされている。クラスター計算から求められた各分子軌道の波動関数に対して、O 2p軌道からの寄与をMulliken population analysisにより見積もったところ、t_2ｇとe_gの各軌道について、それぞれ、4％と30％となり、まさに、t_2ｇ軌道が局在性を示し、e_g軌道がO 2p軌道と強く混成していることを示す計算結果が得られている。t_2ｇ軌道はO 2p軌道との混成が弱いものの、プロファイルにおいては、クラスターモデルと孤立イオンの違いがPz=1.5a.u.付近のピークにはっきりと見られる。e_x²−_y²軌道については、プロファイルに構造こそ見られないものの、混成による波動関数の空間的広がりを反映して、Pz=0a.u.でピークがより高くなり幅が狭くなっているのが分かる。e3_z²−_r²軌道にはもっとも顕著な変化が見られる。クラスター計算によるプロファイルには、散乱ベクトル、即ち［001］軸方向に沿ったMn-Oの結合による振動的な構造が現れている。特に、Pz=2 a.u.付近のピークが、孤立イオンの場合に比べ大きくなっている。プロファイルにおけるこれらの特徴は、フィッティング解析上、e_x²−_y²軌道とe3_z²−_r²軌道を区別するのに非常に有効に作用した。
　では、フィッティング解析の結果説明に移ろう。前述のように、測定されたMCPは、それぞれ、ホール濃度から見積もられたMn 3d電子数で規格化してあるが、解析にあたっては、t_2ｇ軌道はすべて占有されているものと仮定して、その占有数を3に固定し、残りの部分を2つのe_g軌道でフィットした。解析結果は、先程の図4と5の中に実線で示されている。右側のパネルは孤立イオンの計算結果から求めたプロファイルで解析したもので、全体にフィットは良くない。特に、e3_z²−_r²軌道については負の値を示しており、物理的にも無意味な結果となっている。これに比べ、左側のパネルに示したクラスター計算から求めたプロファイルによる解析は、非常に良いフィットを与えている。これは、MCP解析におけるクラスター計算の有効性を示すと同時に、MCPがMn 3dとO 2pの混成を反映していることを明確に示すものである。フィッティングされた各軌道プロファイルの面積から、x＝0.35の試料については、e_x²−_y²軌道の占有数が0.46±0.03、e3_z²−_r²軌道の占有数が0.19±0.03と求められ、同様に、x＝0.42の試料については、e_x²−_y²軌道の占有数が0.44±0.03、e3_z²−_r²軌道の占有数が0.14±0.03と求められた。この結果は、2つのe_g軌道のうち、e_x²−_y²軌道が優勢であることを示しており、従って、DE機構によるab面内での強磁性の安定化に寄与しているものと考えられる^{［17, 26］}［17］K. Hirota et al.：J. Phys. Soc. Jpn. 67（1998）3380.
［26］M. Kubota et al.：J. Phys. Soc. Jpn. 69（2000）1606.。また、e_x²−_y²軌道の占有数がホール濃度の増加によってあまり変化しないのに対して、e3_z²−_r²軌道の占有数は減少している。これは、x＝0.4の試料で、角度分解光電子分光によって観測されている擬ギャップと関連しているのではないかと思われる^［18］［18］D. S. Dessau et al.：Phys. Rev. Lett. 81（1998）192.。x²-y²対称性を持ったバンド中に擬ギャップがあることが示唆されており、そのため、ホールをドープしても、e_x²−_y²軌道の占有数はあまり変化せず、e3_z²−_r²軌道の電子が優先的に除かれるのではないかと考えられるのである。e3_z²−_r²軌道の占有数が減少すると、ｃ軸に沿ったMnO₂面間の強磁性的結合が弱くなり、次第にt_2ｇスピン間の超交換相互作用による反強磁性的結合が優勢になってくるであろう。このようなe_g軌道状態の変化は、ホール濃度の増加につれて、磁気構造が面内強磁性からキャント反強磁性を経てA−type反強磁性へ変化してゆくことと深く関連しているものと考えられる。


4．まとめ
　我々は、層状ペロフスカイトMn酸化物：La_2-2ｘSr_1+2xMn₂O₇（x＝0.35, 0.42）の軌道状態を調べるために、その［001］軸方向においてＭＣＰ測定を行い、また、クラスター計算から求めた理論的なプロファイルをフィッティング解析に応用することによって、e_x²−_y²軌道とe3_z²−_r²軌道の占有数を区別して求めた。その結果として、ＭＣＰは、Mn 3d軌道とO 2p軌道の混成を反映していること、2つのe_g軌道のうちe_x²−_y²軌道が優勢でありホール濃度に寄らず占有数がほぼ一定であること、従って、ホールはe3_z²−_r²軌道に入ってゆくことを明らかにできた。ホールドープに伴うe_g軌道状態の変化については様々な実験事実から推測されてきたが、今回、より直接的に検証できたものと考えている。今後、ホール濃度の低い試料（x＝0.3）についての測定を予定しており、この系の軌道状態について、さらに系統的な情報を提供できるものと期待している。また、この研究を通じて、ＭＣＰ測定が軌道状態を調べるための有効な研究手段の一つであることを示せたのではないかと思っているが、軌道状態や伝導現象が磁性と深く関わり合っている他の磁性物質の研究にも応用してゆきたいと考えている。


5．謝辞
　この研究を行うにあたり、多くの方にご協力を頂きました。実験に関しては、水牧仁一朗氏、桜井吉晴氏、伊藤真義氏（以上、JASRI）のご協力を頂きました。また、クラスター計算に関連して、島 信幸氏（姫工大理）、高田康民氏、堀田貴嗣氏（以上、東大物性研）には、有益なご議論を頂きました。ここに深く感謝いたします。また、この研究は、文部省科学研究費補助金 及び CRESTの援助のもとに行われました。




参考文献
［1］C. Zener：Phys. Rev. 82（1951）403.
［2］P. W. Anderson and H. Hasegawa：Phys. Rev. 100（1955）675.
［3］P. -G. de Gennes：Phys. Rev. 118（1960）141.
［4］A. J. Millis et al.：Phys. Rev. Lett. 74（1995）5144.
［5］H. Koizumi et al.：Phys. Rev. Lett. 80（1998）4518.
［6］Y. Murakami et al.：Phys. Rev. Lett. 80（1998）1932.
［7］Y. Murakami et al.：Phys. Rev. Lett. 81（1998）582.
［8］S. Ishihara et al.：Phys. Rev. Lett. 80（1998）3799.
［9］S. Ishihara et al.：Phys. Rev. B 58（1998）13442.
［10］A. Koizumi et al.：Phys. Rev. Lett. 86（2001）5589.
［11］N. Sakai：J. Appl. Cryst. 29（1996）81.
［12］P. Eisenberger and P. M. Platzman：Phys. Rev. A 2（1970）415.
［13］Y. Moritomo et al.：Nature  380（1996）141.
［14］J. F. Mitchel et al.：Phys. Rev. Lett. 55（1997）63.
［15］D. N. Argyriou et al.：Phys. Rev. Lett. 78（1997）1568.
［16］D. N. Argyriou et al.：Phys. Rev. B 55（1997）R11965.
［17］K. Hirota et al.：J. Phys. Soc. Jpn.  67（1998）3380.
［18］D. S. Dessau et al.：Phys. Rev. Lett. 81（1998）192.
［19］T. Okuda et al.：Phys. Rev. B 60（1999）3370.
［20］K. Hirota et al.：J. Phys. Soc. Jpn.  68（1999）1463.
［21］M. Kubota et al.：J. Phys. Soc. Jpn. 68（1999）2202.
［22］M. Kubota et al.：J. Phys. Chem. Solids 60（1999）1161.
［23］H. Fujioka et al.：J. Phys. Chem. Solids 60（1999）1165.
［24］T. Ishikawa et al.：Phys. Rev. B 62（2000）12354.
［25］Q. Li et al.：Phys. Rev. B 63（2000）024417.
［26］M. Kubota et al.：J. Phys. Soc. Jpn. 69（2000）1606.
［27］M. Kubota et al.：J. Phys. Soc. Jpn. 69（2000）1986.
［28］M. W. Schmidt et al.：J. Comput. Chem. 14（1993）1347.
［29］A. Schäfer et al.：J. Chem. Phys. 100（1994）5829.




小泉　昭久　KOIZUMI Akihisa
姫路工業大学　理学部　助手
〒678-1297　兵庫県赤穂郡上郡町光都3-2-1
TEL：0791-58-0529　FAX：0791-58-0146
e-mail：akihisa@sci.himeji-tech.ac.jp


宮木　智　MIYAKI Satoru
姫路工業大学大学院　博士課程
〒678-1297　兵庫県赤穂郡上郡町光都3-2-1
TEL：0791-58-0101(433）　FAX：0791-58-0570
e-mail：miyaki@sci.himeji-tech.ac.jp


角谷　幸信　KAKUTANI Yukinobu
姫路工業大学大学院　博士課程
〒678-1297　兵庫県赤穂郡上郡町光都3-2-1
TEL：0791-58-0101(431）　FAX：0791-58-0146
e-mail：yukinobu@sci.himeji-tech.ac.jp


小泉　裕康　KOIZUMI Hiroyasu
姫路工業大学　理学部　助手
〒678-1297　兵庫県赤穂郡上郡町光都3-2-1
TEL：0791-58-0147　FAX：0791-58-0570
e-mail：koizumi@sci.himeji-tech.ac.jp


馬越　健次　MAKOSHI Kenji
姫路工業大学　理学部　教授
〒678-1297　兵庫県赤穂郡上郡町光都3-2-1
TEL：0791-58-0151　FAX：0791-58-0570
e-mail：makoshi@sci.himeji-tech.ac.jp


坂井　信彦　SAKAI Nobuhiko
姫路工業大学　理学部　教授
〒678-1297　兵庫県赤穂郡上郡町光都3-2-1
TEL：0791-58-0144　FAX：0791-58-0146
e-mail：n_sakai@sci.himeji-tech.ac.jp


平岡　望　HIRAOKA Nozomu
（財）高輝度光科学研究センター　研究協力員
〒679-5198　兵庫県佐用郡三日月町光都1-1-1
TEL：0791-58-4122　FAX：0791-58-1845
e-mail：hiraoka@spring8.or.jp


廣田　和馬　HIROTA Kazuma
東北大学大学院　理学研究科　助教授
〒980-8578　宮城県仙台市青葉区荒巻字青葉
TEL：022-217-6486　FAX：022-217-6489
e-mail：hirota@iiyo.phys.tohoku.ac.jp


村上　洋一　MURAKAMI Youichi
東北大学大学院　理学研究科　教授
〒980-8578　　宮城県仙台市青葉区荒巻字青葉
TEL：022-217-6485　FAX：022-217-6489
e-mail：murakami@iiyo.phys.tohoku.ac.jp