Volume 06, No.5 Pages 372 - 376

序
　光電子のエネルギーと放出角度を分析することにより、物質の種々の性質を電子・原子レベルで解明することができるため、光電子分光は放射光技術の発展とあいまって近年非常な発展を遂げている。最近は、光電子を結像して微小領域を顕微鏡観察する光電子顕微鏡も登場して、さらに分析領域の幅を拡大している。
　我々はSPring-8のBL25SUに新しい型の二次元表示型球面鏡アナライザを設置して円偏光光電子回折の実験等を進めているが、立ち上げ段階も終わり、最近立体原子顕微鏡などの成果も出始めた。この分析器は従来の二次元表示型球面鏡分析器に様々な改良を施したものであるので、ここではどのような点が新しくなっていてどのような性能を持っているかについて解説する。
　光電子分析器は、検出立体角で大きく分けると、（1）ある狭い角度範囲のみを検出して放出角度依存性を測定する「角度分解型」、（2）非常に広い範囲の角度を一度に測定して電子状態密度を測定する「角度積分型」、（3）二次元検出器を使って非常に広い範囲の角度分布を一度に測定できる「二次元表示型」の三種類になる^［註］。角度分解型では同心半球型分析器が、角度積分型では円筒鏡型分析器（CMA）が最もよく用いられている。これらは、ある放出角度の周り数度の範囲で（対称軸を持つ場合はその周り全ての角で）光電子を一点に収束する二重収束が実現されていて、明るい分析器である。
　角度積分型のCMAは検出立体角が0.2πsr程度と大きい。角度分解型の分析器は、光電子の放出角度依存性を測定するために角度分解能をよくする必要があり、検出立体角は±1°程度と小さく、立体角に直すと0.0003πsr程度である。


二次元表示型分析器
　広い角度範囲を一度に分析する二次元表示型の分析器として、回転楕円鏡型分析器^［1，2］［1］D. E. Eastman, J. J. Donelon, N. C. Hien and F. J. Himpsel : Nucl. Instrum. Methods 172 (1980) 327.
［2］T. Dutemeyer, C. Quitmann, M. Kitz, K. Dornemann, L. S. O. Johansson and B. Reihl : Rev. Sci. Instrum. 72 (2001) 2638. と球面鏡型分析器^［3，4］［3］H. Daimon : Rev. Sci. Instrum. 59 (1988) 545. [Erratum: Rev. Sci. Instrum. 61 (1990) 205.］
［4］H. Daimon and S. Ino : Rev. Sci. Instrum. 61 (1) (1990) 57.がある。回転楕円鏡型分析器はEastman等^［1］［1］D. E. Eastman, J. J. Donelon, N. C. Hien and F. J. Himpsel : Nucl. Instrum. Methods 172 (1980) 327.が1980年に発明したもので、回転楕円面の一つの焦点から出た電子が、もう一つの焦点に集まることを利用して、±45°（0.6πsr）程度の範囲の分析を一度に行っている｡反射鏡は、回転楕円面の電極と、大きさがそれよりも少し小さいグリッドとからなっていて、電子はその間の電場で放物線を描いて反射される。光とは軌跡が違うので厳密には収束せず、余り広い立体角での測定はできないことと、像が歪むという欠点がある｡
　「二次元表示型球面鏡分析器」^［3−5］［3］H. Daimon : Rev. Sci. Instrum. 59 (1988) 545. [Erratum: Rev. Sci. Instrum. 61 (1990) 205.］
［4］H. Daimon and S. Ino : Rev. Sci. Instrum. 61 (1) (1990) 57.
［5］M. Kotsugi, Y. Miyatake, K. Enomoto, K. Fukumoto, A. Kobayashi, T. Nakatani, Y. Saitoh, T. Matsushita, S. Imada, T. Furuhata, S. Suga, K. Soda, M. Jinno, T. Hirano, K. Hattori and H. Daimon : Nucl. Instr. Meth. Phys. Res. (2001) in print.は、我々が独自に開発したもので、像の歪みが無く、より広い立体角±60°（1πsr）で二次元的に表示することができる。SPring-8のBL25SUに設置してあるものは、さらに広い立体角（±80°（1.7πsr））で測定できるように設計してある｡これらは角度の情報が保存されているため、角度分解型の分析器を並列に並べて一度に測定していることになり、測定効率は立体角の比だけ高く、数千倍になっている。


二次元表示型球面鏡分析器
　図1に、この分析器の概念図を示す。図1（a）は従来型のもの^［4］［4］H. Daimon and S. Ino : Rev. Sci. Instrum. 61 (1) (1990) 57.で、（b）はSPring-8のBL25SUに特別に作成したもの^［5］［5］M. Kotsugi, Y. Miyatake, K. Enomoto, K. Fukumoto, A. Kobayashi, T. Nakatani, Y. Saitoh, T. Matsushita, S. Imada, T. Furuhata, S. Suga, K. Soda, M. Jinno, T. Hirano, K. Hattori and H. Daimon : Nucl. Instr. Meth. Phys. Res. (2001) in print.である。スケールを見てわかるように、SPring-8のものは、従来のものより3倍ほど大きい。しかし、どちらも構成はほとんど同じで、主に半球型のメイングリッドと、半径がその約2倍の外球電極および障害リングとからなる。試料からメイングリッドまでは通常接地してあり、試料から出た電子はメイングリッドまで直線軌道を描く｡メイングリッドを通過すると、外球および障害リングにかけてある負の電位による電場で反射されて、出口のアパチャーAに集束する。それぞれの障害リング電極は、試料とアパチャーAを結ぶ線（その中心をＯとする）に対して軸対称になっており、その内側の面はOを中心とする球面であって、その半径に応じた電圧がかけてある。メイングリッドの中心もＯであるため、構造は一見複雑だが、この間の電場は単純な球対称電場になっている。ガードリングは、端の電場が球対称からずれるのを防ぐためのものである。球対称電場による中心力を受けるため、この中での電子の軌道は、ケプラーの法則に従う楕円軌道である。




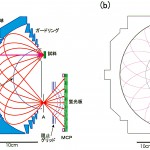
図1　二次元表示型球面鏡分析器。（a）従来型、（b）SPring-8型。


　アパチャーAを通り抜けた電子のうち、阻止グリッドを通過したものは、2枚のマイクロチャネルプレートMCPで増幅され、蛍光板で光のパルスとなって観測される。蛍光板で光るパルスの数および位置は、真空の外からCCDカメラシステムを用いて測定している。
　試料から出たときの方向とアパチャーに入る方向が厳密に等しく並行であるので、蛍光板上で観測される角度分布は試料から出たときの角度分布と厳密に等しくなっている。つまり、スクリーン上の像が全く歪んでいないのがこの分析器の大きな特長である。試料からどの角度に出た電子もAに厳密に収束するため、角度範囲をいくらでも大きくとることができる。入手可能なMCPの大きさと阻止グリッドの半径との兼ね合いで検出角度範囲が決められていて、通常は、±60゜程度である。図1（a）は±50゜の場合を示している。図1（b）では、それよりも外側に出たものもレンズを使ってMCPの方に曲げて検出できるようにしてあり、検出角度範囲が±80゜と過去最大になっている。角度分解能は、Aの大きさとMCPまでの距離、および阻止電位とで決まっており、±0.6゜程度である。
　障害リングは、エネルギーがパスエネルギーより少し大きいものの軌跡を遮る役目を持ち、阻止グリッドはそれより少し小さいエネルギー以下の電子を阻止することができるので、この2つの役割により、ある一定のエネルギーの粒子だけの角度分布パターンを得ることができる。エネルギー分解能は図1（a）でパスエネルギーの1％、図1（b）で0.3％程度である。多くのエネルギー分析器においては、エネルギーの同じものを同じ所に収束し、少し異なるエネルギーのものは少し異なる場所に収束するという「分散性」を利用してエネルギー分析を行っている。この分析器でも、角度の小さい範囲では分散性も利用できるが、全立体角を分析しようとすると逆の分散も入ってきてうまく行かない。異なるエネルギーの電子は収束しないことを利用した「収束非収束」の原理で分光しても良いが、分解能を上げるために上記のように「ハイパスフィルター」と「ローパスフィルター」の効果でエネルギー分析を行っている｡
　励起光は図1（a）のSRのように電極に開けてある穴を通して入れる。図1（a）には描いてないが、グリッドの中にはLEEDパターンやオージェ分光の測定のため電子銃が入っている。このような小さなものはシールドしておけばグリッドの中に入れることができる。ただし、蛍光板上の像はその立体角の所だけ影ができる。図1（b）では、電子銃のメンテナンスを容易にするために、電子銃を分析器の外に出し、90°偏向器を使用して試料に電子を照射している。
　図1（b）の新しい分析器では、エネルギー分解能を高めるために、工作精度を数十ミクロンに高め、メイングリッドと障害リングの作成にあたって特殊な方法を用いている。


グリッド
　図1（b）にあるようにメイングリッドは半径150mmと大きいので、従来のメッシュでは精度良く形を保つことが困難である。従って、厚さ0.4mmのTiの板を成形して、電子ビームで0.4mmの穴を0.7mm間隔で開け、さらにエッチングで穴径を0.5mmまで広げて作成した｡写真を図2に示す｡




図2　メイングリッド


　透過率は40％と見積もられる｡グリッドの周りには19重のガードリングが見えているが、グリッドの後ろが透けて見えていないことからわかるように、透過率はあまり良いとは言えない｡
　グリッドの左上のところに、光を通す穴が黒く見えている。従来は図1（a）のように分析器に垂直に放射光を導入していたが、この分析器では円偏光の特性を活かすために45°斜めに入射している｡
　阻止グリッドも角度分解能を高めるために特殊なものを製作している。3枚のグリッドで構成されており、1枚目と3枚目は半径が14と23mmで、常に接地されている。2枚目のグリッドは半径が20ｍｍで、パスエネルギーより0.05％低い電位になっている。このグリッドは厚さ0.4ｍｍのTiで作られており、電子ビーム加工でやはり0.4ｍｍの穴を開け、さらに両面にメッシュを貼って作成している｡これらのメッシュは#165のステンレス製である。


障害リング
　図3に、外球および障害リングの写真を示す｡外球はアルミでできており、その表面に障害リングが機械加工で形成してある。異なる電位をかけるために、それぞれの障害リングは絶縁する必要があり、そのためにアルミの上にセラミックをコーティングし、その上に金を蒸着して電極としている｡写真で白く見えているのがセラミックの膜である。別々の部品を組み合わせるのでは精度がでないので、このような複雑な工程を経ても一体加工で精度を出す方法を選択した｡障害リングの数は、図1（a）では外球も入れて13対であったが、（b）では10倍の127対に増加している。内側の球面の右上のところに、光を通す穴が黒く見えている｡




図3　外球と障害リング

　前述のように、障害リングの内面は、試料とAとの中点を中心とする球面の一部である。図１(a)でわかるように、その断面は先端がとがっているが、その先端を結ぶ曲線の式は、球面の半径をRとし、水平から測った先端の角度をθとすると

R（θ）=150×｛2.00075−0.1341sin²θ＋0.0133sin^2.55θcos²θ｝

で表される。この曲線は、分析器を通るパスエネルギーをE_pとすると、それより0.05％高い運動エネルギーを持つ電子の軌道の包絡線になっている。それぞれの障害リングにかける電位をVとすると、



で与えられる｡


その他の改良点
　出口のアパチャーＡの大きさが小さいとエネルギー分解能は高くなるが暗くなる。光電子の強度によって最適な明るさと分解能を選ぶことができるように、直径0.2ｍｍから2倍ごとに6.4ｍｍまで6種類のアパチャーを真空の外から交換可能にしてある。
　地磁気その他の磁場を除くために、厚さ2ｍｍのµメタルを50ｍｍの間隔をあけて３重にしてシールドしている｡その結果、分析器が大きくなったこととあいまって、真空層の大きさが直径1ｍという大きいものになってしまった。その装置全体は、光と分析器の位置を合わせるために、上下左右に微動できるようになっている。


立体原子顕微鏡
　この分析器で測定した最近の例として、原子配列の立体写真を初めて測定することができた^［6］［6］H. Daimon : Phys. Rev. Lett. 86 (2001) 2034.ので紹介する。図4（a），（b）は、この装置を用いて測定したＷ（110）面のＷ原子の4f軌道から放出された光電子の放出角度分布パターンであり、この一組で立体写真になっている。運動エネルギーは800eVである。（a），（b）は、回転の向きが反対の円偏光を用いて測定したものである。（a），（b）のパターン中のピークの位置はそれぞれの原子の場所を表しており、2枚の写真の中で少しずれている。このずれが立体視の時の視差角になっており、これらの写真は立体写真になっている。（a）を左目、（b）を右目で見ることにより、結晶中のある原子から回りの原子を見たときの原子の配列が立体的に歪み無く認識できる。視差角による立体的な位置だけでなく、近くの原子が大きく見えることも、原子を立体観察したであろう時と同様である。




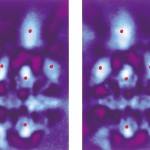
図4（a）,（b）は回転の向きが反対の円偏光を用いて測定したＷ（110）面のＷ原子の4f軌道から放出された光電子の放出角度分布パターン^［6］［6］H. Daimon : Phys. Rev. Lett. 86 (2001) 2034.。（a）,（b）は結晶中のある原子から回りの原子を見た立体写真になっており、（a）を左目、（b）を右目で見ることにより、回りの原子の位置が立体的に認識できる。


終わりに
　本装置はBL25SUに設置されており、そこで利用できる光は500eV以上の円偏光なので、その研究は円偏光の光電子回折の実験に限定されている。しかし、より低エネルギーの直線偏光を励起光に用いれば、電子の軌道解析もできる価電子バンドやフェルミ面の2次元マッピングができ、電子状態の研究に強力なツールにもなる。将来は光電子顕微鏡の機能も持たせ、サブミクロンから原子レベルの顕微鏡としての活躍も期待している｡
　本装置の製作は島津製作所が行い、立ち上げは阪大の小嗣真人君が主に行った｡また、奈良先端科学技術大学院大学の宮武　優、榎本一紀、服部　賢、JASRIの中谷　健、松下智裕、斎藤裕児の諸氏、阪大の菅　滋正教授とその研究室の諸氏には立ち上げにあたり大変お世話になりました。改めて感謝致します｡
^［註］中間の1次元分析器や、広い範囲ではないが角度とエネルギーの二次元分析器もある。




参考文献
［1］D. E. Eastman, J. J. Donelon, N. C. Hien and F. J. Himpsel : Nucl. Instrum. Methods 172 (1980) 327.
［2］T. Dutemeyer, C. Quitmann, M. Kitz, K. Dornemann, L. S. O. Johansson and B. Reihl : Rev. Sci. Instrum. 72 (2001) 2638.
［3］H. Daimon : Rev. Sci. Instrum. 59 (1988) 545. [Erratum: Rev. Sci. Instrum. 61 (1990) 205.］
［4］H. Daimon and S. Ino : Rev. Sci. Instrum. 61 (1) (1990) 57.
［5］M. Kotsugi, Y. Miyatake, K. Enomoto, K. Fukumoto, A. Kobayashi, T. Nakatani, Y. Saitoh, T. Matsushita, S. Imada, T. Furuhata, S. Suga, K. Soda, M. Jinno, T. Hirano, K. Hattori and H. Daimon : Nucl. Instr. Meth. Phys. Res. (2001) in print.
［6］H. Daimon : Phys. Rev. Lett. 86 (2001) 2034.





大門　寛　DAIMON  Hiroshi
奈良先端科学技術大学院大学　物質創成科学研究科
〒630-0101　奈良県生駒市高山町8916-5
TEL：0743-72-6020　FAX：0743-72-6029
e-mail：daimon@ms.aist-nara.ac.jp
http://mswebs.aist-nara.ac.jp/LABs/daimon/index-j.html