Volume 06, No.4 Pages 275 - 279

1．はじめに
　コンプトン散乱実験データの解析及び考察を支援するプログラム、BANDS01、がBL08Wユーザー居室のコンピュータ（Alpha21264, Linux）に導入された。このプログラムは、波動関数を計算するバンド計算プログラムとその波動関数からコンプトン及び磁気コンプトン・プロファイルを計算するプログラムで構成されている。これまでBL08Wでは標準的なデータ解析プログラムの提供などユーザーの便宜をはかることで、未経験ユーザーに対するコンプトン散乱実験の敷居を低くするよう努めてきたが、この計算プログラム群の導入により今後さらに共同利用研究の幅が広がることを期待したい。
　今回導入したバンド計算プログラムは密度汎関数理論に基づく局所密度近似（LDA）によって電子状態を自己無撞着に計算するものである。フルポテンシャル線形化APW（FLAPW）バンド計算法により価電子だけでなく内殻電子の波動関数も計算しており、内殻電子が関与してくる高エネルギーの実験との比較にも適している。バンド計算法として確立している標準的な計算プログラムであり、バンド計算の専門家でなくても使いこなせるプログラムとなっている。
　実験家自身がこのような計算プログラムを使用することで精密かつ迅速に実験と理論を比較することができ、対象とする物質の性質がより詳しくかつ効率よく解明される。また、理論と実験の詳細な比較がなされることにより、理論の不十分な部分が具体的に分かり、さらに進んだ理論・計算方法の開発にも役立つ。コンプトン散乱の実験は波動関数についての情報を定量的に得る数少ない実験方法の一つであり、LDAによって得られる波動関数の良し悪しが明らかになって、次の理論的ステップへの力になると期待される。
　現在、バンド計算プログラムで得られる波動関数から、主としてコンプトン及び磁気コンプトン・プロファイルを計算するプログラムが用意されている。将来的には、コンプトン散乱実験に限らず、この波動関数から様々な実験観測量が計算できるように、計算機能を拡張することを考えている。そこで、読者（ユーザー）から今後の機能拡張についてご意見、ご希望などが頂戴できるように、2．ではプログラムの概要を少し詳しく述べる。3．では計算例を示すことで同プログラム群が正常に動作していることを確認し、4．で今後の発展について述べる。そして、最後に、ユーザーの方々に、同プログラム群の改良に関して、ご理解とご協力をお願いして結びにしたい。


2．プログラムの概要
　BANDS01は“Band Analyses for Newmaterials Design System”の頭文字をとったものであり、FLAPW法によるバンド計算と、それに基づいてコンプトン・プロファイル及び磁気コンプトン・プロファイルの計算を行うことができる。また、将来的には、電子状態から様々な物性を予測し、新しい機能性材料を開発する際の支援システムになることを目指している。本システムは機能別に整理された表1のプログラム群から構成されている。今回導入したのは、そのうち◎印をつけたプログラム群である。これらのプログラム群を分類すれば、wycoff.zdからbnpw.zdまでがバンド計算の前処理、fl00.zd, fl02.zdがバンド計算本体、bnscis.zd, bndope.zdがバンド計算の後処理、reform.zdからbnef.zdまでが電子状態解析、dflapw.zdからoptra_p2l.zsが物性、cpmd.zdからcp_p2l.zsまでがコンプトン・プロファイルとなる。これらの分類はそれほど厳密なものではない。プログラム間が入り組んでがんじがらめになっているのではなく、むしろ比較的フラットなプログラム構成になっているのが特色の一つである。本システムは、機能別に分割された比較的小さなプログラム群より構成されているので、各プログラムのユーザー入力データは比較的少数で済み、従って入力ミスが少なくて済むという利点がある。また、段階的に計算を進めることができるというのも大きな利点といえよう。また、これはプログラムの保守、改良、機能追加の際にも利点になっている。
　結晶構造を指定するために空間群の知識が必要であることが、バンド計算をするうえでのハードルの一つになっているが、本システムでは対話プログラムwycoff.zdを用意して、空間群についてそれほど深い理解がなくても利用できるようにユーザーを支援している。すなわち、空間群番号を入力することにより、International Tables for Crystallography^［1］［1］Theo Hahn ed.：International Tables for Crystallography, Vol. A,（Kluwer Academic Publishers, Dordrecht, 1989）で採用されている原点に対するその空間群の生成元を自動生成する機能、またはWyckoff letterを入力することにより原子座標を設定する機能があるので、ユーザーフレンドリーな入力が可能になっている。また、生成元を直接入力することも可能なので、ユーザー独自の原点を使用した設定もできる。このように幅広いユーザーに対応できるユーザーインターフェイスとなっているのも特色の一つである。なお、本バンド計算プログラムの原型および群論に関するコード^［2］［2］柳瀬 章：空間群のプログラムTSPACE、（裳華房、Tokyo, 1995）は柳瀬 章先生が開発されたものである。
　次にコンプトン・プロファイルを計算するプログラムの概要を述べよう。表1に示したように、スピン依存運動量密度の計算、格子調和関数の計算、スピン依存動径運動量密度の計算、スピン依存コンプトン・プロファイルの計算、コンプトン・プロファイルの計算、磁気コンプトン・プロファイルの計算などのプログラムより構成されている。なお現状では価電子のみを対象としており、内殻電子に対する計算は今後の開発に残されている。


表1　プログラム一覧　




　本システムでのコンプトン・プロファイルの計算方法の特徴は、運動量密度を格子調和関数で展開する点にある。よく知られているように、コンプトン・プロファイルを計算するには散乱ベクトルに垂直な面での運動量密度に関する2重積分が必要となる。しかしながら、いったん運動量密度を格子調和関数で展開しておけば、コンプトン・プロファイルは1重積分で求めることができるので極めて短時間に計算することができる。したがって、多くの散乱ベクトルに対するコンプトン・プロファイルを計算する場合、この計算方法は極めて有利である。近年、精密なコンプトン・プロファイルの実験から、3次元運動量密度分布の再構成が行われている。そのためには、多くの散乱ベクトルに対するコンプトン・プロファイルが必要になるので、どのような散乱ベクトルに対するコンプトン・プロファイルを測定すれば3次元運動量密度が適切に再構成されるかを、あらかじめシミュレーションしておくことは実験を計画する上で有用と思われる。


3．計算例
　磁気コンプトン散乱実験の標準試料であるbcc-Feの磁気コンプトン・プロファイルを計算した。14方位の結晶方位について計算を行った。図1にその結果を示す。磁気コンプトン・プロファイルの形状が方位によって変化しているが、この傾向はTanakaら^［3］［3］Y. Tanaka, N. Sakai, Y. Kubo and H. Kawata：Phys. Rev. Lett. 70（1993）1537.による実験結果とバンド計算の結果をよく再現している。また、最近、話題になっている超伝導体物質、MgB₂、について、バンド計算とコンプトン・プロファイルの計算を行った。そのうち、図2にバンド構造図（E-k曲線）を示す。この結果はKortusら^［4］［4］J. Kortus, I. I. Mazin, K. D. Belashchenko, V. P. Antropov and L. L. Boyer：Phys. Rev. Lett. 86（2001）4656.のバンド計算結果と一致しており、Γ-A方向に2次元的なホール面が2つ存在していることがわかる。このように、上の2例に限らず、今回導入したプログラム群は正常に動作していることを確認している。




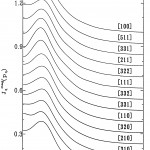
図1



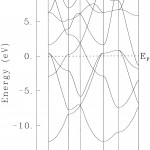
図2



4．今後の展望
　今後の展望として、まず本プログラム群の根幹であるバンド計算プログラムについて述べてみたい。密度汎関数法によるバンド計算では、各原子のまわりの波動関数は実際よりも広がって計算される傾向にある。これは過去の実験と理論の比較によってある程度分かっているが、今回のコンプトン・プロファイル計算プログラムによってさらに詳しい情報が得られると期待される。LDAの欠点に対応するために、短期的にはLDA+Uバンド計算法ないしはその改良を行って対処し、長期的には密度汎関数理論を離れ多体量子論の原点に戻ってGW近似やさらに進んだ近似による計算方法を開発していくことが考えられる。
　LDA+Uバンド計算法は、比較的局在したd電子やf電子のエネルギーを、軌道に依存したポテンシャルを導入することにより改良するものである。これが波動関数の形まで改良するかどうかは分からないが、この方法を延長することにより波動関数の改良まで持って行きたい。また、内殻電子のエネルギー準位は、LDAでは1％位の誤差があり、深い準位になると何百eVも実験と異なることになる。定量的比較という意味ではこのような所も改良していくことが必要となる。
　GW近似によるバンド計算は、実験家が実用的バンド計算として利用するにはまだ少し時間がかかるが、実用化の時代はもう開かれつつあると言える。この時問題になるのは膨大な計算量を処理する計算機の問題と、計算の非専門家が使用できるような使いやすいプログラムを開発することである。計算機はどんどん安くなっており、並列化技術と組み合わせることにより、計算可能な領域を増やして行くことができる。これにはバンド計算の研究者だけでなく専門のプログラマの力を借りて、より有効な計算プログラムを開発して行くことが重要となる。また、使いやすいプログラム開発の面でもプログラマの応援は欠かせない。

　次に、物性を計算するプログラムについて述べよう。LDA（将来的にはLDA+U、GW近似）バンド計算で求めた波動関数から、（磁気）コンプトン・プロファイルに加えて、様々な実験スペクトルや物理量が計算できるような機能を整備することは多くのユーザーにとって有益なことであろう。例えば、放射光を用いたX線非弾性散乱実験や核共鳴散乱実験で得られるフォノンの解析には、理論計算により求めたフォノン分散、フォノン状態密度や電子-フォノン結合定数が有用になると考えられる。また、X線非弾性散乱実験で得られる電子励起スペクトルを、LDAさらにはGW近似で計算できるようになれば強相関系物質の電子状態の研究がさらに発展すると期待される。物性を計算するプログラムの具体的な拡張に関しては、ユーザーの要望を取り入れて進めていきたい。


5．おわりに
　本プログラムの開発者・管理者は、できるだけ多くのユーザーに使って頂き、ユーザーの意見や希望をどんどん取り入れて、より使いやすくかつ信頼できるプログラムになるよう改良していきたいと考えています。現在のプログラムは計算の専門家が作ったものであり、プログラムの内容を知っているものが使用してきました。本プログラムには計算を失敗しないための仕組みが考慮されていますが十分ではなく、思わぬ落とし穴が潜んでいるかもしれません。利用にあたって、問題や疑問な点があれば、どのような細かいことでも結構ですので、担当者にお知らせくださるようお願いします。



参考文献
［1］Theo Hahn ed.：International Tables for Crystallography, Vol. A,（Kluwer Academic Publishers, Dordrecht, 1989）
［2］柳瀬 章：空間群のプログラムTSPACE、（裳華房、Tokyo, 1995）
［3］Y. Tanaka, N. Sakai, Y. Kubo and H. Kawata：Phys. Rev. Lett. 70（1993）1537.
［4］J. Kortus, I. I. Mazin, K. D. Belashchenko, V. P. Antropov and L. L. Boyer：Phys. Rev. Lett. 86（2001）4656.




櫻井　吉晴　SAKURAI  Yoshiharu
（財）高輝度光科学研究センター　放射光研究所　利用研究促進部門I
〒679-5198　兵庫県佐用郡三日月町光都1-1-1
TEL：0791-58-0802（3803）　FAX：0791-58-0830
e-mail： sakurai@spring8.or.jp


伊藤　真義　ITOU  Masayoshi
（財）高輝度光科学研究センター　放射光研究所　利用研究促進部門I
〒679-5198　兵庫県佐用郡三日月町光都1-1-1
TEL：0791-58-0802（3908）　FAX：0791-58-0830
e-mail：mito@spring8.or.jp


浜田　典昭　HAMADA  Noriaki
東京理科大学　理工学部　物理学科
〒278-8510　千葉県野田市山崎2641
TEL：0471-24-1501（3219）　FAX：0471-23-9361
e-mail：hamada@ph.noda.sut.ac.jp


小玉　祥生　KODAMA  Akio
㈱富士総合研究所　フロンティア・サイエンス室
〒101-8443　東京都千代田区神田錦町2-3
TEL：03-5281-5425　FAX：03-5281-5414
e-mail：kodama@star.fuji-ric.co.jp


小泉　昭久　KOIZUMI  Akihisa
姫路工業大学　理学部
〒678-1297　兵庫県赤穂郡上郡町光都3-2-1
TEL：0791-58-0529　FAX：0791-58-0146
e-mail：akihisa@sci.himeji-tech.ac.jp