Volume 03, No.2 Pages 34 - 38

1．はじめに
　磁気モーメントは電荷に較べて非常に弱いＸ線散乱体である。散乱断面積はτ²r_e²の程度であるが、硬Ｘ線領域ではτ～10^－2なので、電子の電荷散乱断面積（r_e²）より4桁小さい。τ＝hω／mc²（これは、光子エネルギーと静止電子のエネルギーの比に等しい）。このため、従来、物質の磁気構造解析は中性子線の独壇場であった。しかし、共鳴磁気散乱の発見^［1］と第3世代放射光々源の出現により、Ｘ線磁気散乱が新しい原子レベルの磁気構造プローブとして登場した。Ｘ線磁気散乱は、①精密ゴニオメトリーにより高運動量分解能が実現できる、②微小角配置でモノレーヤの表面敏感性が得られる、③原子の吸収端で起こる共鳴散乱に原子選択性がある、 ④大きな散乱ベクトルが使えるので高実空間分解能が得られる、⑤スピンと軌道モーメントの分離決定が可能である、⑥試料が小体積で足りるなど、中性子散乱や他の方法に見られない特長をもち、薄膜や表面の磁気構造解析を画期的に発展させると期待される。 
 
2．共鳴Ｘ線磁気散乱
　我々はＸ線散乱によりFe／Gd多層膜の磁気構造を解析している。本題に入る前に、Ｘ線磁気散乱の性質につい　て少し述べる。
　原子の散乱因子f は　
　
　　f ＝f ₀＋f _c’＋if _c”＋i（f _m’＋if _m”＋f_m^non） （1）　
 
と書ける。f ₀はトムソン散乱（＝－r_eZ）、f _c’とf _c” は異常分散補正、f _m’とf _m”は共鳴磁気散乱、f_m^nonは非共鳴磁気散乱を表わす。右辺の前半は電荷散乱、後半は磁気散乱に対応する。f _c’、f_c”、f_m’、f _m”は原子の吸収端で大きくなる共鳴項である。上に述べた τr_eはf_m^nonの大きさである。f _m’とf _m”の正確な大きさは良く分からないが、オーダーはf_m^nonと同程度である。（1）から分かるように、電荷散乱と磁気散乱は位相が90゜異なるので、逆空間の同じ場所に生じても干渉しない。位相を合せれば干渉が起こり、大きな信号（共鳴磁気電荷干渉散乱）が得られるが、それには、①Ｘ線エネルギーを磁性原子の吸収端に同調し共鳴散乱を起こさせる、②入射Ｘ線に円偏光を用いる、などの方法がある^［2］。放射光の連続スペクトルは①に好都合である。ふつうの放射光は直線偏光である。この場合、共鳴磁気電荷干渉散乱の強度（非対称比）はtan2θに比例し、多層膜のブラッグ反射が現われる小角領域で弱くなってしまう（2θは散乱角）。一方、円偏光に対する非対称比の散乱角依存性はcos2θである。①と②を合わせて用いれば、多層膜から強い共鳴干渉散乱を観測することが可能になる。
　全散乱強度は純電荷散乱（オーダー1）、磁気電荷干渉散乱（オーダーτ）、純磁気散乱（オーダーτ²）の3つを含む。強磁性体結晶のように電荷と磁気モーメントが同一の空間分布をもつ場合、磁気散乱は電荷散乱と逆空間で重なり、後者に圧倒されて検出できない。これを分離するのに磁場反転法が使われる。試料にプラス方向の磁場かけて測定した散乱強度をI ^＋、マイナス磁場で測定した強度をI ^－とすると、純電荷散乱は磁場の向きに依らないので、差強度（I ^＋－I ^－）は磁気電荷干渉散乱だけを含む。しかし、不飽和磁性体では外部磁場の反転によって電子スピンの方向が一斉に反転するとは限らない。円偏光のヘリシティ反転は磁気モーメント反転と同じ効果をもつので、左右の円偏光を用いて差強度を測定する方が望ましい。
　共鳴Ｘ線磁気散乱は原子の内殻電子が外殻（あるいはバンド）の非占有状態へ電気多重極遷移し、元の状態へ戻るときに生じる弾性散乱である。外殻がスピン分極していること、内殻がスピン－軌道結合でエネルギー分裂していることが、強い共鳴磁気散乱が起きる必要条件である。内殻と外殻の電子状態が関与するので、共鳴磁気散乱の理論を開発した Hannonらはexchange scattering と名付けた^［3］。上に述べた強い散乱の条件は、XMCD（Ｘ線磁気円二色性）の条件に他ならない。「吸収は散乱角ゼロの散乱」と考えれば、理解されよう。　 
 
3．Fe／Gd多層膜の磁気構造
　Gdは室温附近にキュリー点をもつ強磁性体である。4f不対電子に由来するGdの磁気モーメントは Feの3dモーメントよりかなり大きな温度変化を示す。GdとFeの磁気結合は反強磁性的なので、Feと Gdを交互に積層した薄膜中ではμ_Feとμ_Gdは反対方向を向こうとする（μ_XはＸ層の磁気モーメント）。 Feを最外層とし、室温でμ_Fe＞μ_Gd、低温でμ_Fe＜μ_Gdの多層膜を考え、試料表面に平行に外部磁場Hをかける。室温ではμ_FeがHと平行、μ_Gdが反平行のFe 整列状態、低温ではμ_GdがHと平行、μ_Feが反平行の Gd整列状態が安定である（図1）。Fe整列状態の多層膜を冷却すると、μ_Fe～μ_Gdとなる補償温度T comp 附近で、μ_Feとμ_Gdの両方がHに対して傾いた「捩れ状態」（twisted state）に転移する。モーメントの向きはゼーマン・エネルギーと交換相互作用エネルギーのバランスで決まるが、μ_Fe～μ_Gdの温度域では μ_Feのμ_Gd方が磁場と平行、他方が反平行の状態より双方が傾いた方がエネルギー和が小さくなる。「捩れ状態」が出現するのは、Gd原子間の強磁性結合がFe－Fe間の強磁性結合、Fe－Gd間の反強磁性結合よりかなり弱いためである。多層膜内部のFe層は膜の両側でGd層と磁気結合しているのに対し、表面のFe層は片側にしかGd層が無いのでμ_Feの方向を比較的変え易い。「表面捩れ状態」は表面近傍層だけで磁気モーメントが捩れた状態である。Fe／ Gdのこのような磁気構造転移は磁場の変化でも起こり、図2のような相図が計算されている^［4］。捩れ状態の存在はスピン偏極中性子散乱やγ線45゜入射メスバウアー実験で確かめられている。　
 
 
    
 
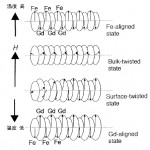
図1 Fe／Gd多層膜の磁気構造。最外層はFe層。矢印は各薄膜の磁気モーメントの大きさと方向を示す。
 

 
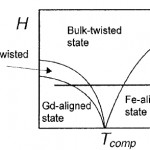
図2 Fe／Gd多層膜の（T、H）磁気相図。図4の測定は、この図のH =2.4kOeの断面（図中の水平直線）に相当する。  
 
4．円偏光を用いたFe／Gd多層膜の共鳴磁気散乱
　我々はSi基板上に作成した［Fe（35Å）／Gd（50Å）］₁₅のGd共鳴条件におけるＸ線鏡面反射を円偏光を用いて測定し、多層膜内の磁化分布、捩れ状態の温度変化を調べた。米国アルゴンヌ国立研究所 のAdvanced Photon Sourceのアンジュレータ・ラインで実験を行った。アンジュレータ間隔を調整し、第1高調波バンドのピーク・エネルギーを7.2keVに合せた。低温シリコン・モノクロメータで単色化した直線偏光ビームを（111）ダイアモンド位相遅延子を透過させ、円偏光にした。（111）ブラッグ条件の近傍で結晶をピエゾ素子でμrad程度回転することにより、右円偏光と左円偏光を素速く切換えることができる。試料（4×4mm）は永久磁石とともに Displexクライオスタット内に入れ、4軸ゴニオメータのφ軸上に搭載した。磁場は試料表面に平行にかかる。GdL ₃磁気円二色吸収スペクトル（XMCD）を測定し、ピーク位置（7.243keV）にＸ線エネルギーを合せた。θ-2θスキャン法で鏡面反射を測定したが、各θ-2θステップで光子ヘリシティを切換えてI ^＋とI ^－を測定した。I ^＋は右円偏光の散乱強度、I ^－は左円偏光の散乱強度である。（I ^＋＋I ^－）／2 は純電荷散乱、（I ^＋－I ^－）／2 は磁気電荷干渉散乱を与える。散乱光の偏光を分析しない我々の実験では、 I ^＋－I ^－は

 -2（k＋k’cos2θ）（F _c’F_m'＋F _c”F_m”） （2）

 に比例する^［5］。F ’、F ”は多層膜の構造因子の実数部と虚数部、添字c、mはそれぞれ電荷散乱、磁気散乱を表わす。磁気散乱の構造因子Fmは多層膜内のGdスピンの総和で決まる方向を向いたベクトルである（Feの非共鳴磁気散乱を無視する）。k＋k’ cos2θは散乱面（kとk’で定義される面）に平行なベクトルであるから、Fe／Gd多層膜が整列状態にあるならば、外部磁場が散乱面に垂直な配置（φ =90°）では（2）のベクトル内積がゼロになるのでI ^＋＋I ^－＝0、平行な配置（φ=0°）では≠0になる（図3）。「捩れ状態」ではμ_Gdが磁場に対して有限の角度を成すので、両配置でI ^＋－I ^－≠0になる。また、強度比から捩れ角が決められる^［6］。 　
 
　
  
 
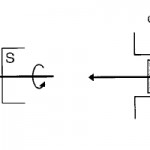
図3 （a）：φ=0°配置、（b）：φ=90°配置。Ｘ線散乱面が外部磁場と（a）では平行、（b）では垂直。
 
5．Gd膜の磁化構造　
　磁場2.4kOe で測定されたI ^＋－I ^－の1～4次のブラッグ反射をそれぞれのI ^＋－I ^－で規格化し、温度T ＝ 240、180、160、140Kについて図4に示す。φ=90° 配置のデータから、T ≧180Kでμ_Gdが磁場に整列していること、T ≦160Kでは捩れていることが分かる。非対称比（I ^＋－I ^－）／（I ^＋＋I ^－）は2％以下で、これはXMCDのピーク値と同程度である。φ=0°、90° 両配置でブラッグ・ピークの符号が＋、－、＋、－になっている。これを説明するには、厚さ50Åの Gd膜が膜厚方向に凹型の磁化分布を持つと仮定しなければならない。すなわち、Gdの磁化はFe層との界面近傍で大きく、膜厚の中央附近で小さい。指数関数a＋exp（－bt）を膜厚の中央（t ＝1／2）で折返した関数をGd磁化プロフィルとして（I ^＋－I ^－）／（I ^＋＋I ^－）を計算すると、実験がかなり良く再現される（図5）。図6はこのようにして決めたa、b 値から構成したGd層の厚み方向の磁化分布モデルである。T ≧180Kの整列状態（aligned state）ではGd層は外部磁場と反平行に磁化している。捩れ状態の磁化分布は温度T に依存し、補償温度T _comp（＝170K）に近いT ＝160K ではFe層との界面近傍でだけ捩れているが、T _compよりかなり低いT ＝140Kでは捩れ角が増し、膜厚の中央附近ではモーメントが外部磁場に対して垂直になっている。 　
 
  
 
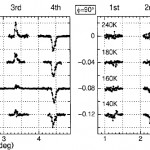
図4 ［Ｆe（35Å）／Ｇd（50Å）］₁₅多層膜の共鳴Ｘ線磁気散乱（GdL₃吸収端で測定）。左図：φ=0°、右図：φ=90°配置。図中の数字は試料温度。磁場の強さ2.4kOe。測定はブラッグ反射の周辺だけで行なわれている。φ=90°配置では240K、180Kでノイズを越える信号は出ていない。
 
 
 
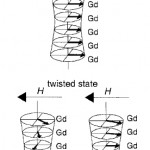
図6 図5に対応するＧd層（平均厚さ50Å）の磁化モデル。H は外部磁場の方向を示す。図の上下方向は膜厚方向であり、各図の上下にFe層がある。 
 
 
6．今後の方向と展望　
　以上の実験は、Gdの2p_3/2→5d電気双極子遷移に際して起きる共鳴磁気散乱を通してGd膜の磁化を見ている。Fe膜の磁性を調べるにはFeK 吸収端（7.11keV）で同様な実験を行えば良い。Feの1sレベルにはスピン－軌道結合によるエネルギー分裂が無いので、GdL 吸収端ほど強い共鳴磁気散乱は期待できないが、実験は十分可能である。
　磁気散乱の計算にはf _m’とf _m”の値が必要である。しかし、これらは良く分かっていない。f _m”は XMCDに関連する量であるが、GdのXMCDには混乱があり、符号さえ確かでなかった^［7］。混乱の一因はI ^＋とI ^－の定義にある。我々は「磁場Hと入射Ｘ線の波数ベクトルkの内積（H・k）が正の配置でヘリシティ＋1の円偏光で測定されたＸ線強度をI ^＋と定義」している。ヘリシティ＋1の円偏光の電気ベクトルEは、ビームに垂直にスクリーンを立て、これを線源側から見ると、スクリーン上で時計周りに回転する。我々はこれを右円偏光と呼んでいる（これはXMCDで使われている慣行とは異なる）。（H・k）＝0 の場合には任意性があるが、我々は、試料を散乱ベクトルqの矢印先端から見たとき、Hがkから時計周りに回っている配置でヘリシティ＋1の入射Ｘ線で測定された散乱強度をI ^＋とする。このようにすれば、実験上明らかな量でI ^＋とI ^-が定義され、測定結果から磁気モーメントの方向が一義的に決まる。我々はXMCD測定からf _m”値を決め、これをKramers-Kronig 変換してf _m’値を求める試みを行なっている。
　図5の計算は、I ^＋＋I ^－データをフィットして求めた多層膜試料の化学構造に基づいているが、このモデルは15枚のFe膜、Gd膜が、それぞれ均一で等しい原子密度分布を持つと仮定している。実際には Fe／Gd界面での原子拡散はかなり著しく^［8］、また、各膜の密度が等しい保証はない。磁気電荷干渉散乱データから磁気構造を精密に決めるためには、まず、化学構造（原子の分布）を決めなければならない。
　磁性層／磁性層、磁性層／非磁性層の界面におけるスピン配列の乱れは薄膜の磁性に大きな影響を及ぼす。我々は、原子の密度分布で表わされる化学ラフネスとは別にスピンの分布で決まる磁気ラフネスが存在し、巨大磁気抵抗膜やトンネル接合素子におけるスピン偏極電子の界面散乱を支配しているのではないかと考えている。磁気ラフネスの情報は鏡面反射の周囲に現われる磁気散漫散乱から得られる。しかし、散漫散乱のI ^＋－I ^－は第3世代放射光々源でも非常に弱く、長時間をかけなければqの大きな領域で統計精度の高いデータは得られない。
　Ｘ線磁気散乱のユニークさは界面磁気ラフネスの決定ができるだけではない。超高真空試料作成設備と組合せれば、表面の磁気構造が調べられる。反強磁性体の磁気トランケーション・ロッドは2、3の結晶について測定されているが、超薄磁性膜や超構造単原子層膜の磁気散乱測定は将来の課題である。その設備がSPring-8に設置され、表面磁気Ｘ線回折・散乱実験が可能になることを期待している。「その場」表面試料作成、超高真空Ｘ線散乱・回折、低温、磁場を組合せた装置は複雑であるが、要素技術は確立している。3d遷移金属のK 吸収端、4fランタナイドのL 吸収端、アクチナイドL 吸収端は4.5～26.6 keVのエネルギー範囲にあるので、ほとんど全ての磁性原子が共鳴磁気散乱で調べられる。表面・界面磁気散乱は第3世代放射光源から得られる高輝度、高平行性、連続スペクトル、高偏光性のＸ線無くしては実行不可能であり、また、これらを他の実験より優れて活用するものである。
　共同研究者の細糸信好（京大化研）、並河一道（東京学芸大）、石松直樹（東工大総理D2）、坂田修身（東工大応セラ研）、岩住俊明（物構研）、G.Srajerグループ（APS）の諸氏に感謝する。   
 
   
 
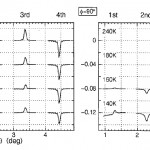
図5 ［Ｆe（35Å）／Ｇd（50Å）］₁₅多層膜の磁気電荷干渉散乱のモデル計算。左図：φ=0°、右図：φ=90°配置。図中の数字は試料温度。原子振動は考慮していない。
 
文　献
［1］K.Namikawa,M.Ando,T.Nakajima and H.Kawata,J.Phys.Soc.Jpn.54,4099（1985）
［2］S.W.Lovesey and S.P.Collins,X-ray Scatteringand Absorption by Magnetic Materials（Oxford
Sci.Press,1996）
［3］J.P.Hannon,G.T.Trammell,M.Blume and D.Gibbs,Phys.Rev.Lett.61,1245（1988）
［4］R.E.Camley and D.R.Tilley,Phys.Rev.B 37,3413（1988）
［5］H.Hashizume,N.Ishimatsu,O.Sakata,N.Hosoito et al., Jpn.J.Appl.Phys.36,4252（1997）
［6］H.Hashizume,N.Ishimatsu,O.Sakata,T.Iizuka et al., Physica B（in press）
［7］小谷章雄、PF研究会「円偏光軟Ｘ線放射光を利用する磁性研究の展望」、平成9年10月； H.
Matsuyama,I.Harada and A.Kotani,J.Phys.Soc.Jpn.66,337（1997）
［8］D.R.Lee,Y.J.Park,S.H.Park,Y.H.Jeon et al.,Physica B（in press）
 
［追記］
偏光を考慮した原子散乱因子は
 
  

である。は反射光、入射光の偏光ベクトル（添え字ν’、νはそれぞれの偏光状態）、 は磁気モーメントに平行な単位ベクトルである。本分の（1）は（3）の簡約形である。図5の計算はGd散乱因子に（3）を用い、f ₀＝－64、f _c’＝27.60、f _c”＝18.93、
f _m’＝－0.02、f _m”＝－0.06とした。

  
  
 

橋爪　弘雄　HASHIZUME Hiroo
東京工業大学
応用セラミックス研究所教授
〒226-8503 横浜市緑区長津田町
TEL：045-924-5333
FAX：045-924-5339
e-mail：hhashizu@n.cc.titech.ac.jp
略歴：1969年東京大学工学系大学院博士課程終了、1982年東京工業大学助教授。