Volume 03, No.2 Pages 29 - 33

1．はじめに
　希土類金属および化合物のL 吸収端における磁気円偏光二色性（MCD）の研究のこれまでの歩みを振り返ってみると、混乱と誤解の連続であったことに改めて驚きを禁じえない。その混乱の原因は、以下にまとめるように複数のことがらが微妙に絡み合っているのであるが、最も重要なことは、実験家と理論家の間の協力関係と意思の疎通の不十分さにあったと思われる。ものごとの真相がようやく見えてきた今、これまでの研究の経過を整理して纏めておくことは、今後、同様な混乱が生じないためにも必要であろう。それは、この問題の解決に多少なりとも携わった研究者としての義務のようなものであると考え、筆者らはこの小文を執筆することにした。
　まず最初に、MCDの符合の定義から始めよう。 Baudeletら（以下では、最初の二人の著者名のイニシャルをとってBGと記す）は、1993年に出版された彼等のレビュー論文の冒頭で次のように述べている^［1］。“In the following we report the difference between the absorption spectra recorded for two opposite directions of the applied magnetic field with the same photon helicity: Δμ＝μ^－（B＋）－μ^－（B－）（which is equivalent to Δμ=μ^＋（B－）－μ^＋（B＋）orΔμ＝μ^＋（B－）－μ^－（B－）＝－μ^＋（B＋）＋μ^－（B＋））. This convention is used by almost all the groups working on the subject and should never be changed!”（下線は筆者）これは単に定義の問題であるから、逆の符合の定義をする人がいても物理の中味が変わるわけではない。しかし、その人はいちいち「私の定義はこれこれである」と断わらなければ混乱が生じる。いや、実際には断わっていても混乱が生じたのであって、それについては後程述べる。勿論、すべての研究者が、共通の定義を用いることが望ましいことは言うまでもない。BGは上記の文章に続いて“In order to avoid any confusion we want to precisely state again the type of convention we use. The axis of quantization is taken as +0z which is the direction of the photons wave vector (k): it is also the direction in which we apply the magnetic field B+ and, in the absence of magnetic anisotropy it is also the direction of magnetization M.”と書いている。
　勿論、L 吸収端におけるMCD研究のこれまでの混乱は、単に上記定義の混乱だけに因るわけではない。以下、順を追って問題を整理し、解決への道筋をたどって行こう。　
　
2．簡単な例　
　さて、最も簡単な例として、4 f 電子が完全に満ちたLuFe₂の場合を考えてみる^［1］。BGにしたがい、量子化軸と入射光の方向を＋z（BGの記号では＋0z）方向にとる。外部磁場を＋z方向にかけると磁気モーメントは＋z方向を向き、系の磁気モーメントは殆どがFeの3d 電子によって担われているから、Fe の3d 電子スピンは－z方向を向く。Feの3d 電子とLu の5d 電子のスピンは反強磁性的に結合することがよく知られており、したがってLuの5d 電子スピンは＋z方向に分極する。これは、Feからの内部磁場によってLuの5d バンドが交換分裂し、アップスピン（↑）バンドのエネルギーがダウンスピン（↓）バンドより低くなるので、フェルミ準位まで電子をつめる（Lu原子あたり約１個の5d 電子が存在する）と↑電子の数が↓電子より多くなることを意味する。
　さて、LuのL₃ 電気双極子遷移吸収を考えると、 ヘリシティーの光によって5d の↑状態への遷移がより強く起り、ヘリシティーでは↓状態への遷移がより強く生じる。5d バンドは分極していて、 ↓電子の空席が↑電子より多いから、ヘリシティーの光がより強い吸収をうけ、MCDの積分強度は Δμ＞0となる。L₂ 吸収では、逆にヘリシティーの光によって5d の↑状態への遷移がより強く起り、 ヘリシティーでは↓状態への遷移がより強く生じるので、Δμ＜0である。この結果はBGの実験結果とよく一致し、上記の機構が正しいことを裏付けている。  
　次に、4 f 状態が4 f ⁷配置をとるため軌道磁気モーメントが消失しているGdを考える。GdFe₂では、系の磁化は主としてGd4 f 電子によって担われている。したがって、＋z方向の外部磁場によってGdの4 f スピンは－z方向を向く。
　4 f と5d の原子内交換相互作用は強磁性的であるから、5d スピンは－z方向（5d 磁気モーメントは＋ z方向）に分極し、5d バンドのゼーマン分裂はLuFe₂ の場合と丁度逆になることがわかる。それ故、L₃の MCDはΔμ＜0、L ₂はΔμ＞0となる筈であるが、この結果はBGの実験結果と一致しない^［1］。この点について、BGは“We obtain the wrong direction for the 5d magnetic moment. Indeed, only transitions to↓ spins are observed, which means that the 5d moment is along -0z, which is incorrect.”（下線は筆者）と述べている。つまり、実験結果は5d 磁気モーメントが－z方向を向いているように見えているのであるが、勿論そんな筈はない。何故だろうか？　　
 
 
　　　
　
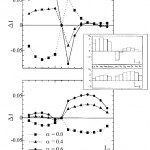
図1 全希土類イオンにおけるL ₂、L ₃吸収端MCD スペクトルの積分強度ΔI。αは新しく導入された電気双極子遷移行列要素の増大効果を表すパラメーター。挿入図はJIの計算結果^［2］で、MCDの符号の定義が逆にとられている。

 
3．理論の定式化
　上記のGdに対するMCDの定性的な機構を、すべての希土類元素に対して定量的に計算するための理論を城と今田（以下JIと記す）が提案した^［2］。希土類の4 f 状態はフント則にしたがうものとし、外部磁場の方向に4 f 磁気モーメントが向くと、原子的な 5d の一電子準位E（m_z, s_z）が4 f －5d交換相互作用によって決められる。JIは個々のE（m_z, s_z）を中心に有限のバンド幅をもつ5d バンドを作り、そこに一定数の電子をつめた後、 2p －5d 光学遷移によるMCDを求めた。計算されたL₂とL₃のMCDの積分強度は図1の挿入図に示されている。ただし、JIのMCDの符合はBGとは逆に定義されているため、Gdで L₂が負、L₃が正になっていることに注意する必要がある。JIは彼等の計算結果がFischer らの一連の希土類（RE）に対する（RE）₂ Co₁₇のMCDの実験結果^［3］と概ね一致すると述べているが、これは正しくない。Gdの例からもわかるように、MCDの符合の定義が逆であるために、たまたま一致しているように見えるだけである。

　最近、圓山らは（RE）₂Fe₁₄Bについて系統的にL 吸収端のMCDの測定を行った。その結果を図2に示す。これをJIの理論と比較すれば、 MCDの符合が殆ど逆転しており、一方希土類元素の違いによるMCDの絶対値の変化は概ね一致していることがわかる。ただし、（RE）₂Fe₁₄Bでは、外部磁場の方向に磁化されるのはREではなくFeの磁気モーメントであることを考えて、Gd～Ybに対してはJIのMCDの符合をいったん逆転させてから実験と比較することが必要である。
　 JIの定式化は4 f 電子に関する簡略化はあるものの、この場合重要な4 f －5d 交換相互作用を系統的に取り入れており、それ自身もっともに見える。この定式化に一体何が欠けているのだろうか。　
 
 
4．問題の解決　
　実は、MCDの逆符合の謎は、Gd金属に関するかぎり、BGの論文より以前に解かれていたのである。 Carraら（1991年）は、Gdの5d 波動関数の動径方向の広がりがスピンに依存することを考慮することにより、MCDの実験結果をよく再現する計算結果を得ている^［4］。4 f －5d 間の交換相互作用のため、 4 f スピンと平行な5d ↓ の波動関数は5d ↑ に比べて空間的広がりが小さく、したがって2 p－5d 間の双極子遷移確率がより大きくなる。そのため、L₃（L₂）吸収における（）ヘリシティーの強度が増強され、MCDの符合が反転する^［5］。BGはCarraらの論文を知っていて、それを引用しているが、しかし逆符合の問題が解決されていることには気付いていない。実際、Carraらの論文には、2 p－5d 双極子遷移によるMCDの符合に関する機構は殆ど説明がなく、双極子遷移と2 p－4 f 四重極遷移のMCDに対する相対的寄与が中心的な主題になっている。
　最近、松山らは、4 f －5 d 交換相互作用による双極子遷移確率の増大効果が単にスピン量子数のみならず磁気量子数にも依存するよう理論を拡張し、 Gd以外の希土類に対してもMCDの系統的な計算をおこなった^［6］。まず、L ₂、L ₃吸収におけるMCD の積分強度計算結果を図1 に示そう。図中、αは双極子遷移確率の増大効果を表す定数で、その効果が積分強度の符号を反転させていることが読みとれる。2．でも述べたように、MCDの積分強度の符号は初期状態における5d 電子のつまり方によって決められる。即ち、4 f －5d 交換相互作用により一電子準位E（m_z, s_z）が下がる状態は占有され、Pauliの原理によりその状態への遷移が減少する。このことは、全ての状態に遷移したとき0となるべき積分強度の正負のバランスが崩れてその符号が決まることを意味する。一方、新しい機構、双極子遷移確率の増大効果は逆に4 f －5d 交換相互作用によりエネルギーの下げられる一電子状態ほど双極子遷移確率が増大され、その状態への遷移が増大する。これらは相反する寄与で、現実の物質では後者の効果が勝って符号が逆転したことを示している。ただし、前にも述べたように、（RE）₂ Fe₁₄BではFeが全磁気モーメントを担うので、Gd～Ybに対してMCDの符合を逆転させてから実験結果と比較することが必要である。
　全く同じ頃、van Veenendaalのグループも基本的に同じ機構による解決策を提案し、同様な結論に達した^［7］。ただし、彼らは初期状態における5 d 電子の存在を無視したため、そのスペクトルには上に述べたそれぞれの寄与の競合から来る多様性が取り入れられていない。この多様性は具体的なスペクトルの再現のためには必要不可欠なものである。　
　一方、具体的なMCDスペクトルの再現のためには電気四重極遷移の寄与も無視できない。これまでも電気四重極遷移の吸収スペクトルへの寄与が、その角度変化などに注目して議論されてきたが、その位置や強度に関して曖昧さは依然として解消されなかった。吸収スペクトルに比べて構造を持つMCD スペクトルはそれらの問題を議論するのに適しており、特に電気双極子遷移によるMCD スペクトルが正しく再現された今、この問題を定量的に議論できる時が来た。実際、図3に示された（Nd）₂ Fe₁₄Bの例に見られるように、電気双極子遷移による吸収より低エネルギー側の構造は明らかに電気四重極遷移の寄与と考えられる。4 f 電子間の強いクーロン相互作用にもかかわらず、電気四重極遷移の寄与がこの様に低いエネルギー領域に来るのは勿論4  f電子に対する強いcore hole potential による。図3のMCDスペクトル（下段）は電気双極子遷移のスペクトル（上段）にCowan program により計算された電気四重極遷移の寄与（中段）を重ね合わせたものである。実験結果と計算結果との一致は満足すべきものである。同様にして得られた他の希土類に対するMCD スペクトルも、Ce など2、3の例外を除き、単に積分強度ばかりでなくそのスペクトルも正しく再現された。　
 
  　
 

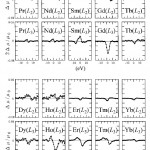
図2 様々な希土類化合物（RE）₂ Fe₁₄BのL ₂、L ₃吸収端におけるMCD スペクトル。μ₀は各々の吸収端での吸収強度の飛び。
 
 
 　
 
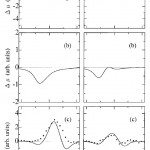
図3 希土類化合物（Nd）₂ Fe₁₄BのL ₂、L ₃吸収端におけるMCDスペクトルの計算結果。各スペクトルはcoreholeの寿命を考慮し半値半幅2eVのLorentzianで、実験の分解能を考慮し半値半幅0.75eVのGaussianでたたみ込まれている。上段の図は電気双極子遷移の寄与を、中段の図は電気四重極遷移の寄与（電気双極子遷移のスペクトルを基準にピーク位置を5eV低エネルギー側にずらせ、ピーク位置での強度を30%にしたもの）を示す。下段の図はそれらを重ね合わせたものであり、黒丸は実験のMCDスペクトルを示す。　
 
5．おわりに
　以上に述べたように、かなりの混乱を経てこの問題の本質的な部分は解決をみた。混乱の原因は　
1）MCDの符合に対する定義の混乱
2）電気双極子遷移と四重極子遷移の共存による混乱
3）二元以上の系で、希土類と他元素の磁気モーメントの競合による混乱
4）4 f －5d 交換相互作用による5 d 状態の磁化効果と2 p－5 d 双極子遷移確率の増強効果の競合による混乱
5）単純な誤解に基づく混乱などに帰せられる。
　最後に、実験家と理論家の協力の重要性を強調したい。van Veenendaalらや松山らは、この協力態勢がよく整っていたために適切な対処ができ、正しい結論をえることができた。一方、JIはBGの実験の論文を知りながら（JIの論文^［2］には参考文献としてBGの論文が引用されている）、計算と実験の不一致に気付かなかったし、BGはCarraらの理論の論文を知りながら、Gdの“wrong direction”の原因が何であるかに気付かなかった。もし、実験と理論の連携がよければ、このようなことはなかったであろう。今後の、研究発展のための一つの指針としたい。　
 
謝辞
この原稿は、岡田耕三、松山広志、福井啓二、J. C. Parlebasの諸氏をはじめとする多くの方々との共同研究を基にしている。厚く感謝の意を表したい。 　
　
　

参考文献　
［1］F. Baudelet, Ch. Giorgetti, S. Pizzini, Ch. Brouder, E. Dartyge, A. Fontaine, J.P. Kappler and G. Krill : J. Electron Spectrosc. Relat. Phenom. 62, 153 （1993）.
［2］T. Jo and S. Imada : J. Phys. Soc. Jpn. 62, 3721 （1993）.
［3］P. Fischer, G. Sch¨utz and G. Wiesinger : Solid State Commun. 76, 777（1990）; P. Fischer, G. Sch¨utz, S. St¨ahler and G. Wiesinger : J. Appl. Phys. 69, 6144 （1991）. 同じ著者達による同じデーターの表示の符号が異なっている。当時の混乱を端的に示している。
［4］P. Carra, B. N. Harmon, B. T. Thole, M. Altarelli and G. A. Sawatzky : Phys. Rev. Lett. 66, 2495 （1991）.
［5］H. König, X. Wang, B. N. Harmon and P. Carra : J. Appl. Phys. 76, 6474（1994）.
［6］H. Matsuyama, I. Harada and A. Kotani : J. Phys. Soc. Jpn. 66, 337（1997）.
［7］M. van Veenendaal, J. B. Goedkoop and B. T. Thole : Phys. Rev. Lett. 78, 1162（1997）. 

 　
　
小谷　章雄　KOTANI Akio
(Vol.3, No.1, P24) 　 
 
 
 
原田　勲　HARADA Isao
昭和19年12月12日生
岡山大学理学部
〒700-8530 岡山市津島中3-1-1
TEL/FAX：086-251-7808
e-mail : harada@cc.okayama-u.ac.jp
略歴：1972年大阪大学大学院基礎工学研究科博士課程修了、1972年神戸大学理学部助手、1990年岡山大学理学部助教授、1996年岡山大学理学部教授、現在に至る。その間、Ohio University客員助教授、Hannover University客員研究員を歴任。　
　
 
 
 　
圓山　裕　MARUYAMA Hiroshi
昭和27年11月19日生
岡山大学理学部
〒700-8530 岡山市津島中3-1-1
TEL：086-251-7823
FAX：086-251-7830
略歴：昭和52年立命館大学理工学部数学物理学科卒業、55年岡山大学大学院理学研究科修士課程修了、56～58年仏国CNRS高磁場研究所客員研究員、60年岡山大学理学部助手、平成5年同助教授。理学博士、日本物理学会、日本放射光学会会員。最近の研究：Ｘ線磁気円二色性およびＸ線共鳴交換散乱による強磁性体のスピン・電子状態の研究。今後の抱負：放射光による金属磁性の研究、特に構造と磁性の相関について微視的観点から調べたい。趣味：読書、音楽鑑賞。