Volume 26, No.1 Pages 16 - 21

1. 熱とフォノン
　近年、デバイス性能向上のために熱の制御が重要となっている。一例をあげると、デバイスの微細化・高集積化に伴い、デバイス内部に熱が蓄積しやすくなっている。このような熱はデバイス特性にとって障害となるため、排熱を効率的に行うことが必要となる。逆の例を挙げると、熱電材料開発においては、熱電効率を上げるため、排熱しにくい材料を用いることが重要となる。
　巨視的に見た場合、熱の伝わり方は熱伝導率κで表現される。熱を速く伝えたい（排熱を速く進めたい）場合には大きなκを持つ素材を、逆に排熱を遅くしたい場合には小さなκを持つ素材を、本来のデバイス特性に加味して選ぶことが重要となる。微視的に見た場合、固体内で熱を伝えるのはエネルギーを持った粒子（電子やフォノン）である。デバイスは通常半導体や絶縁体で構成されており、フェルミ準位付近に熱を伝えるだけの十分な電子が存在しない。従って、主としてフォノンが熱を伝えることになる。フォノンが関与する熱伝導率を格子熱伝導率κ_latと言う。
　格子熱伝導率κ_latは波数q、モードjのフォノンを独立粒子とみなすと、線形ボルツマン方程式より、

･･･ (1)

と書ける^[1][1] G. P. Srivastava: The Physics of Phonons (Taylor & Francis, 1990).。ここでv_q,jはフォノン速度（[v_q,j]_α = ∂E_q,j / ∂q_α）、C_Vq,jは定積比熱（温度TとフォノンエネルギーE_q,jの関数）、は独立粒子フォノンの寿命（緩和時間）である。式(1)はフォノンのエネルギーと寿命が分かれば巨視的な熱伝導が求められることを示す。しかし、この式は2000年代頃まで厳密に計算されてこなかった。これは、式(1)から明らかなように全フォノンが計算に寄与すること、および（後述するように）フォノン寿命の計算が複雑であること、から以前の計算機にはこの式(1)を厳密に計算する能力がなかったことが大きい。従って2000年代以前ではフォノンの詳細はそれほど重視されず、フォノンを議論する際にはフォノン速度v_q,jの大きい音響フォノンを単純化したデバイモデルなどが用いられ、フォノンと熱の詳細な関わりについては十分な検討が行われてこなかった。
　フォノンを説明する最も簡単な近似は調和振動子近似である。この近似下でフォノンは永遠に振動が続く、すなわちフォノン寿命は無限大（ = ∞）であり、式(1)から熱伝導κ_latは無限大となる。しかし、実際の物質では熱伝導は有限で、フォノンには常に寿命がある。この有限のフォノン寿命は、フォノンが他のフォノンや電子・欠陥などで散乱する結果、生じる。フォノン散乱過程を図1にまとめた。フォノンは図1(a)にあるように他のフォノンと相互作用したり（フォノン−フォノン散乱）、図1(b)にあるように（ドープされた半導体試料において）電子と相互作用して（電子格子相互作用。なお、一般にこの電子格子相互作用における熱輸送は電子単体における熱輸送よりも大きな寄与を持つ）寿命を持つ。同様に、図1(c-e)にあるように欠陥や不純物や試料境界でフォノンが散乱する結果、寿命を持つ場合もある。近似的にフォノンの寿命はそれぞれの寿命の寄与の和として表すことができる（Matthiessen則^[2][2] J. M. Ziman: Electrons and Phonons (Oxford, 1960).）。

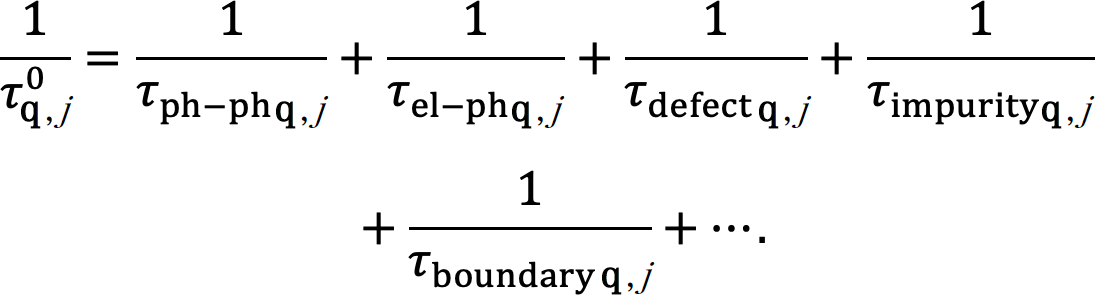･･･ (2)

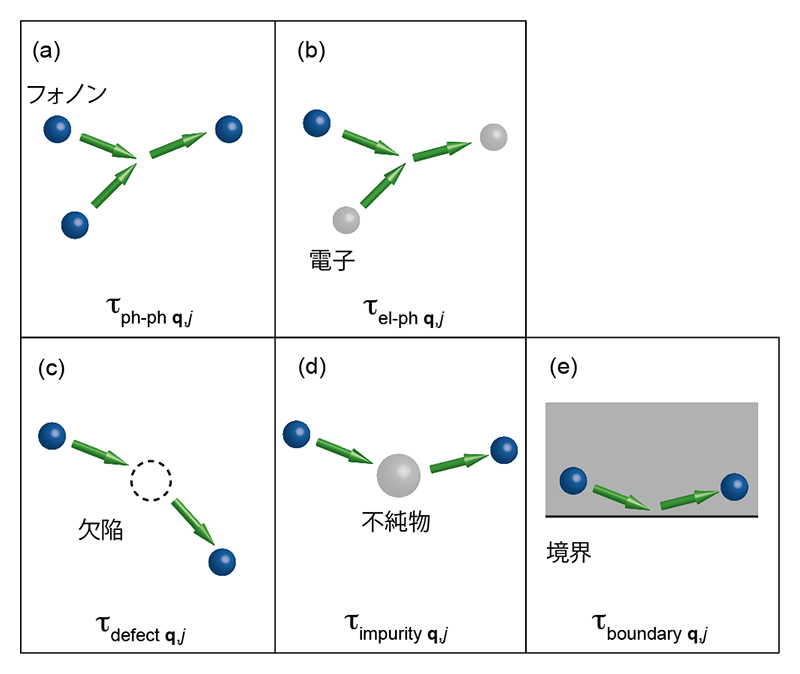
図1　フォノンの散乱機構。(a) フォノン−フォノン散乱、(b) 電子格子相互作用、(c) 欠陥によるフォノン散乱、(d) 不純物によるフォノン散乱、(e) 試料境界によるフォノン散乱。

　例えば、フォノン−フォノン散乱（τ_{ph-ph q,j}）を計算で求める場合、図1(a)からも分かるように、ハミルトニアンの3次の摂動が必要となる。（前述のように）この計算量は膨大で、以前の計算機では算出不能であった。しかし、現在では（任意の波数q、フォノンモードjでの）τ_{ph-ph q,j}の算出は可能となっている。同様に他の散乱機構についても現在の計算機能力で算出可能となってきている。
　なお、このようなフォノン寿命の議論は熱伝導率κ_latだけでなく、極性半導体において高電界中電子と光学フォノンとの相互作用を議論する際にも重要となる（詳細については文献[3,4]などを参照）。

2. フォノン測定
　実験で得られるフォノン線幅γからは全寿命（ = ħ / γ）を評価することができる。したがって、計算結果と実験結果を比較することにより、図1(a-e)のどのフォノン散乱機構が熱伝導に寄与しているかを調べることができる。そのような知見はデバイス開発にとって重要な指標を与える。
　一般的にフォノン情報は、プローブを試料に当てて、出てきたプローブのエネルギーの変化分（E_f−E_i）と運動量変化分（k_f−k_i）を測定することによって得られる（図2）。フォノンを測定するプローブとしては、光、中性子、電子などがある。このうち電子をプローブとする手法は一般的に侵入長が最も短く（～Åオーダー）、主に表面フォノンの研究に用いられる（EELS; Electron Energy-Loss Spectroscopy）。中性子をプローブとする手法は侵入長が最も長く（通常 >> mm）、フォノン分散を測定する手法としては長い歴史を有している（非弾性中性子散乱（INS; Inelastic Neutron Scattering）法）。

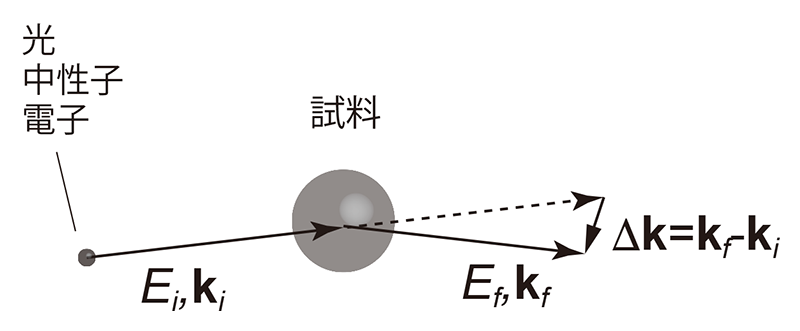
図2　フォノン測定の原理。プローブ（光、中性子など）を試料に当てて、エネルギー変化と運動量変化を測定する。

　光をプローブとする場合、可視光では波長が長く、運動量変化分（k_f−k_i）が常に～0となる。これは逆格子空間上のΓ点に対応する、言い換えると、可視光をプローブとした場合、Γ点のフォノンのみが測定可能であり、それ以外のフォノン分散を見ることは基本できない。これに対して、波長の短いX線を用いて、フォノン分散測定を行う手法がSPring-8 BL35XUやBL43LXUに敷設された非弾性X線散乱（IXS; Inelastic X-ray Scattering）法である。SPring-8ではフォノンが測定できるような高いエネルギー分解能を生み出すために、Siの高次反射を利用しており、主としてエネルギー分解能～1.5 meV（入射エネルギー hν = 21.7 keV、Si(11 11 11)反射）と3 meV（同17.8 keV、Si(9 9 9)反射）の光を用いている^[5][5] A. Q. R. Baron et al.: J. Phys. Chem. Solids 61 (2000) 461-465.。フォノン分散が測定できるという意味では前述のINSやEELSと同じ手法であるが、INSと比較するとX線は集光ができるので微小試料（～20 μm）の測定が可能である。また、電子線に比べてX線はその侵入長が長いので（μm～mmオーダー）、物質のバルクフォノンを測定することができる。
　フォノン寿命に注目すると、従来はRaman散乱分光を用いた研究が多く行われてきた。Raman散乱分光では通常可視光レーザーが用いられることから、Γ点にある光学フォノンの寿命しか情報が得られなかった（例えば、GaN光学フォノンの寿命測定^[6,7][6] K. T. Tsen et al.: Appl. Phys. Lett. 72 (1998) 2132-2134.
[7] D. Y. Song et al.: J. Appl. Phys. 100 (2006) 113504.）。しかし、2010年代に入って、INSやIXSを用いてスペクトル線幅を測定することにより、フォノン寿命を評価し、熱伝導の微視的な起源を明らかにする研究が行われている（例えば、INSによるPbTeの寿命測定^[8][8] O. Delaire et al.: Nat. Mater. 10 (2011) 614-619.）。

3. 薄膜への応用
　前述のように対象物に対するX線の侵入長は、μm～mmオーダーであるが、斜入射X線回折法（GIXRD; Grazing Incidence X-Ray Diffraction）に見られるように、試料表面に対する入射角（α）を臨界角前後まで小さくすると（図3(a)）、侵入長を短くすることができる。この性質を利用することによって薄膜のフォノン計測を行うことが可能となる。本研究に先立つ先行研究としてIXSでも薄膜を対象として、SPring-8^[9,10][9] M. Hoesch et al.: Phys. Rev. B 75 (2007) 140508(R).
[10] H. Xia et al.: Appl. Phys. Lett. 110 (2017) 043102.やESRF^[11,12][11] J. Serrano et al.: Phys. Rev. Lett. 106 (2011) 205501.
[12] F. Caruso et al.: Phys. Rev. Lett. 119 (2017) 017001.ですでにいくつかの報告が行われている。本研究では、GIXRDの知識を元に、より効率的な薄膜フォノンを測定する方法を確立することを目指した。本研究はSPring-8 BL35XUにて行われた。

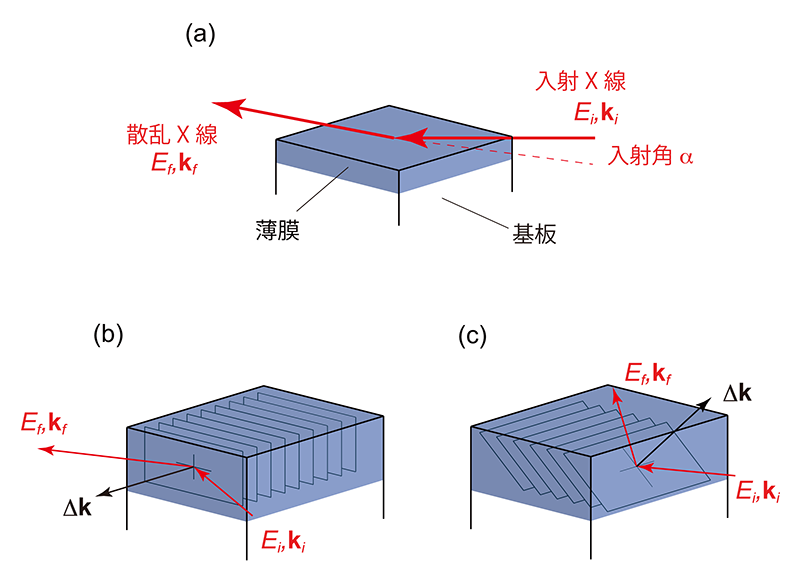
図3　(a) 斜入射条件X線散乱の一般的配置。(b,c) フォノン測定に適した2つの斜入射条件配置：in-plane配置(b)およびout-of-plane配置(c)。

　斜入射条件を維持するためには斜入射角度が精度よく測定できなければならない。20 keV付近のX線では通常臨界角は0.1～0.2°程度であることから、入射角の制御精度として、< ±0.02°程度が必要となる。しかし、従来のBL35XU標準のソフトおよびハードではこの精度を得ることはできなかった。ハードの面から言えば、通常の4軸回折系（2θ, ω, χ, φ）では試料の面方位は求めることができても試料自身の表面の傾きを求めることができない。そのため、入射角に対して最大0.5°程度の誤差が生じる。この誤差は、試料（基板／薄膜）の面方位が試料表面と必ずしも垂直でないことによる影響が大きいと考えられる。この問題を解決するために、通常の4軸回折系に2軸のゴニオメータ（χ_A, φ_A）を追加した（図4(a,b)）。装置の特性上、従来の4軸回折系のうち、ω軸回転には制約（<～20°）があるが、φ軸については360°回転が可能である。φ軸と追加した2軸（χ_A, φ_A）を組み合わせると、φ軸回転に対して90°間隔で入射X線と試料表面が平行になる条件を容易に探し出すことができる。これは（試料が平坦な表面を持っているという仮定の下で）、任意の軸回転（ω, χ, φ, χ_A, φ_A）操作に対して、試料表面の傾きを評価できることを意味する。次にソフト上の問題点であるが、BL35XUで制御に用いているCSS社のspecはその定義で、「入射X線はy軸を逆行し、散乱X線はxy面内にある」としている。しかし、実際の装置ではSi高次反射を利用した背面反射分光器と集光ミラーが試料前の光学系に配置されているため、入射光は試料位置で通常0.2°ほど（図4(c)中、α₀）水平面（同、x’y’平面）からずれている。さらに、検出する散乱光も水平面上にない。バルク試料測定ではα₀を無視し（y軸とy’軸を一致させ）、散乱X線が水平面上にあると近似して、本ソフトを使用しているが、この使用法では入射角を正確に評価することができない。この問題を解決するために、ソフトの定義するデカルト直交座標（xyz）と実験室上の空間を示す直交座標（x’y’z’）（図4(c)）を相互に変換するような一次写像f（およびその逆写像f^-1）をソフト上に組み込むこととした。これらハード面・ソフト面の改良をすることによって、入射角度を±0.02°程度で制御することが可能となった。

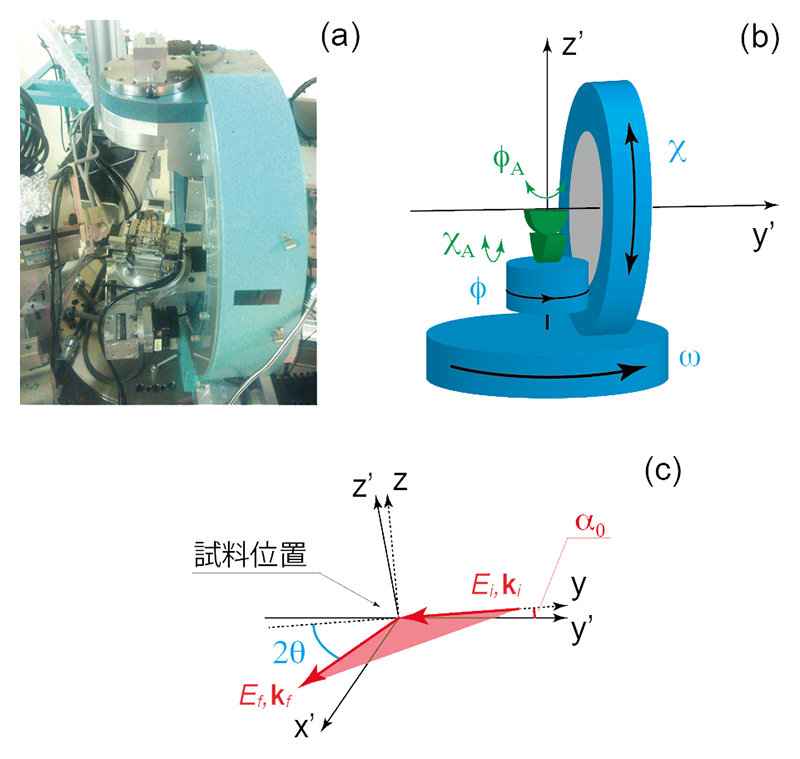
図4　(a,b) 2軸ゴニオメータ（χ_A, ϕ_A）が追加された4軸回折系（2θ, ω, χ, ϕ）：実際の装置写真(a)および回転方向の模式図(b)。従来の回転軸を青色で、追加の回転軸を緑色で示す。(c) 実験室上の空間（x’,y’,z’軸で構成される）とソフトウェア上の空間（xy平面（図中赤色平面）とy,z軸で構成される）。

　GIXRDの場合、基板にX線が到達して基板のBraggピークを検出したとしても、薄膜のBraggピークと基板のBraggピーク位置が逆格子空間上で異なる場合には、薄膜のBraggピークを評価することができる。しかし、フォノン測定の場合にはBrillouin域の全てにフォノンが存在するため、基板にX線が到達してしまうと、基板のフォノンが検出されてしまう。薄膜のフォノンのみを測定するためには基板にX線が入らない配置が必要となる。そのような配置は大きく分けて2つある（図3(b,c)）。1つは基板すれすれにX線を入射し面内の情報を得るin-plane散乱（図3(b)）であり、もう1つは基板すれすれにX線を入射し面内以外の情報を得るout-of-plane配置（図3(c)）である。この2つの配置は実験の目的によって使い分けることができる。例えば、out-of-plane配置では出射角が大きく、多くの散乱光を集めることができるという利点がある。しかし、この配置では基本的にフォノン振動の分極を分けることができず、縦分極（longitudinal phonon mode）と横分極（transverse phonon mode）が同時に観測されるため複雑なフォノン構造を持つ物質には適さない。
　なお、斜入射X線を用いたフォノン測定の場合、臨界角よりも入射角を小さくし、全反射条件になると、侵入長が短くなりすぎ、表面フォノンが観測されてしまう^[13][13] B. M. Murphy et al.: Phys. Rev. Lett. 95 (2005) 256104.。そのため、実験条件は常に臨界角以上であることが求められる。この制約のため、測定可能な膜厚はおおよそ0.5 μm程度が下限となる。特にX線が透過しやすい軽元素（Siなど）薄膜試料の場合、この下限は大きく上昇する。

4. 設定例
　実際の測定例としてHPVE（Hydride Vapor Phase Epitaxy）法で作製された40 μm厚のScN(110)薄膜（基板：サファイアm面）^[14][14] Y. Oshima et al.: J. Appl. Phys. 115 (2014) 153508.を用いた研究を示す^[15][15] H. Uchiyama et al.: Phys. Rev. Lett. 120 (2018) 235901.。ScNはNaCl構造を持ち、窒化物半導体における熱電材料として期待されている物質である^[16-18][16] V. Rawat et al.: J. Appl. Phys. 105 (2009) 024909.
[17] P. V. Burmistrova et al.: J. Appl. Phys. 113 (2013) 153704.
[18] S. Kerdsongpanya et al.: J. Appl. Phys. 120 (2016) 215103.。
　前述のように得られるIXSスペクトルに対して基板のフォノンを排除して、薄膜のフォノンだけを測定する必要がある。そこで、フォノン測定に先立ちBL35XUの装置を用い、GIXRDを行うことにした。入射光として21.747 keVのX線を用いた。
　図5に薄膜（ScN）および基板（サファイア）のGIXRDを示す。測定したBraggピークはScNが(400)（図5(a)）、サファイアが(220)（図5(b)）であり、out-of-plane配置（図3(c)）に対応する。結晶と回折の方向を図5(c)に示す。図5(b)より、入射角を1.7°以下にすれば基板サファイアの寄与を抑えることができることが分かる。そこで入射角αを1.1～1.7°に制御してIXS測定を行うこととした。

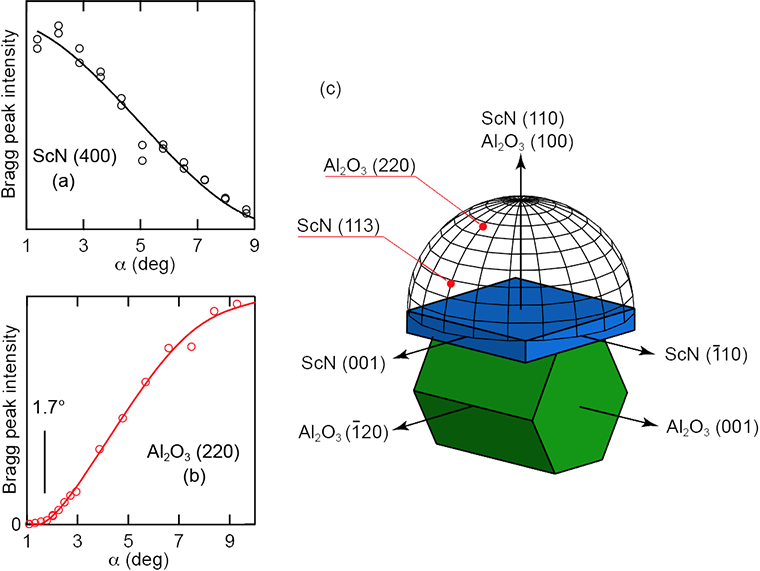
図5　ScN/サファイア基板のGIXRD入射角（α）依存性。(a)および(b)はScN(400)およびサファイア(220)の入射角依存性をそれぞれ示す。(c)は結晶および測定したBragg回折の方位を示す。

　IXS測定結果を図6(a)に、実験的に得られたピーク位置とDFT（density functional theory）計算結果の比較を図6(b)に示す。実験ではout-of-plane配置（図3(c)）を用い、21.747 keV（エネルギー分解能～1.5 meV）のX線を用いた。Γ-Xの方向（図6(a)右）については、Δk = (1 1 3+q)の条件で測定を行い、Γ-K-Xの方向（図6(a)左）については、Δk = (3+q -1-q -1)の条件で室温において測定を行っている。Out-of-plane配置を用いたため、縦分極（longitudinal acoustic phonon（LA）とlongitudinal optical phonon（LO））と横分極のフォノン（transverse acoustic phonon（TA）とtransverse optical phonon（TO））が同時に観測されている。前述のように、このIXS実験ではGIXRDの結果（図5）と組み合わせることによって、高精度な入射角制御を行っている。このため、薄膜測定にも関わらず、従来のバルク結晶測定と同様、効率的な測定が可能となった（図6を得るのにおおよそ3日間を要している）。実験結果について詳細に見ると、得られたフォノンピークは全てScNに帰属でき、基板の寄与がないScN膜のみのフォノン測定に成功したことが分かる（図6(b)）。さらに得られた実験結果とDFT計算がよく一致していることは図6(b)から明らかであり、フォノン分散計算が十分高い精度にあることを示している。

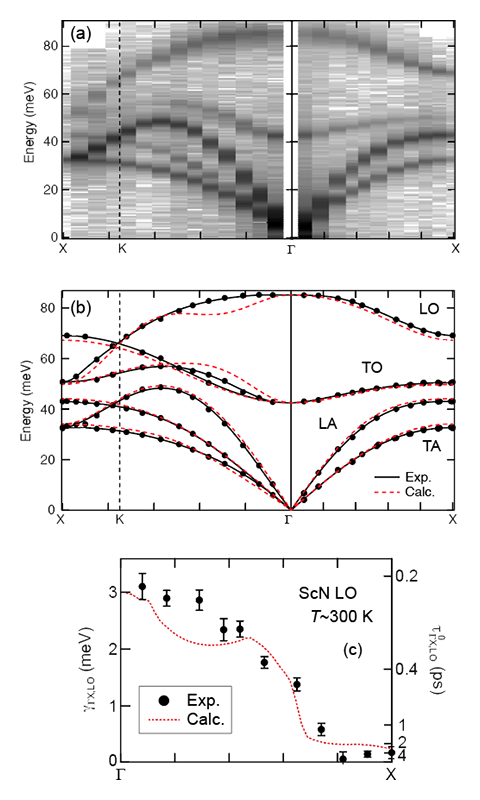
図6　(a) ScN薄膜のIXSスペクトル^[15][15] H. Uchiyama et al.: Phys. Rev. Lett. 120 (2018) 235901.。得られたスペクトルを対数表示している。(b) 実験結果とDFT計算との比較。(c) Γ-X方向（(a,b)の右側）、縦光学フォノンにおけるフォノン線幅（γ）の実験と計算の比較。

　Γ-X方向の縦光学フォノン（LO、図6(a)右）のフォノン線幅に注目すると（図6(c)）、実験から求められた線幅（γ、図6(c)中黒丸）はDFT計算から求められたフォノン−フォノン散乱による寿命（τ_{ph-ph q,j}、図6(c)中赤点線）によく一致しており、この試料のフォノン散乱機構がフォノン−フォノン散乱で説明できることが分かる。実際、この計算から得られる格子熱伝導率は、κ_lat = 43 W/m/K（T = 300 K）であり、実際に測定した同一サンプルの熱伝導とよく一致する（κ = 36.4 W/m/K（室温））。従来の報告ではScN薄膜は比較的熱伝導が低いとされてきた（κ = 10−20 W/m/K^[16-18][16] V. Rawat et al.: J. Appl. Phys. 105 (2009) 024909.
[17] P. V. Burmistrova et al.: J. Appl. Phys. 113 (2013) 153704.
[18] S. Kerdsongpanya et al.: J. Appl. Phys. 120 (2016) 215103.）。しかし、本研究から、フォノン−フォノン散乱のみを考慮した熱伝導率はかなり大きく、今まで得られた低い熱伝導率は別の機構による散乱（例えば、欠陥による散乱（図1(c)）や不純物による散乱（図1(d)））に起因することが明らかになった。

5. おわりに
　このようにX線の特性を生かすことで、よりデバイス環境に近い薄膜材料について、フォノン分散や寿命が評価できるようになった。実験結果を計算と比較することによって、熱特性の微視的な起源についても議論可能となっている。本研究は装置上の改造であることから、他の試料への展開が容易である。実際すでに、外部ユーザーを受け入れ、1 μm厚のHfNやHfN/ScN超格子構造（基板：MgO）の薄膜フォノン分散測定に成功している^[19][19] S. Chakraborty et al.: Appl. Phys. Lett. 117 (2020) 111901.。
　しかしながら、本手法はまだ完成されたとは言い難い。特に入射角を小さくした場合、X線の照射領域（foot print）が伸びることによる迷光の寄与や、室温以上と室温以下での入射角測定の精度が大きく違うこと（冷凍機に適合したゴニオメータがないため）、など未解決の問題は多い。通常のバルク単結晶測定並みの精度で実験が行えるよう、さらなる改善が望まれる。

謝辞
　本研究はJASRI理事長ファンド採択課題「斜入射X線を用いた薄膜フォノンの研究」の一環として行われた。プロジェクトの遂行にあたっては多くの方々に御助言いただいた。関係者の皆様に深く感謝する。実験はBL35XU（課題番号：2015A2030、2015B1980、2016B1495）で行われた。試料提供いただいた物質・材料研究機構の大島祐一氏および島村清史氏、フォノン寿命に関する議論をしていただいたNew South Wales大学のRobert Patterson氏、熱伝導測定を行っていただいた東京大学の岩本壮太郎氏および塩見淳一郎氏にこの場を借りて深く御礼申し上げる。

参考文献
[1] G. P. Srivastava: The Physics of Phonons (Taylor & Francis, 1990).
[2] J. M. Ziman: Electrons and Phonons (Oxford, 1960).
[3] H. Morkoç: Nitride Semiconductor Devices (Wiley-VCH, 2013).
[4] G. Conibeer et al.: Sol. Energy Mater. Sol. Cells 135 (2015) 124-129.
[5] A. Q. R. Baron et al.: J. Phys. Chem. Solids 61 (2000) 461-465.
[6] K. T. Tsen et al.: Appl. Phys. Lett. 72 (1998) 2132-2134.
[7] D. Y. Song et al.: J. Appl. Phys. 100 (2006) 113504.
[8] O. Delaire et al.: Nat. Mater. 10 (2011) 614-619.
[9] M. Hoesch et al.: Phys. Rev. B 75 (2007) 140508(R).
[10] H. Xia et al.: Appl. Phys. Lett. 110 (2017) 043102.
[11] J. Serrano et al.: Phys. Rev. Lett. 106 (2011) 205501.
[12] F. Caruso et al.: Phys. Rev. Lett. 119 (2017) 017001.
[13] B. M. Murphy et al.: Phys. Rev. Lett. 95 (2005) 256104.
[14] Y. Oshima et al.: J. Appl. Phys. 115 (2014) 153508.
[15] H. Uchiyama et al.: Phys. Rev. Lett. 120 (2018) 235901.
[16] V. Rawat et al.: J. Appl. Phys. 105 (2009) 024909.
[17] P. V. Burmistrova et al.: J. Appl. Phys. 113 (2013) 153704.
[18] S. Kerdsongpanya et al.: J. Appl. Phys. 120 (2016) 215103.
[19] S. Chakraborty et al.: Appl. Phys. Lett. 117 (2020) 111901.

内山　裕士　UCHIYAMA Hiroshi
（公財）高輝度光科学研究センター
放射光利用研究基盤センター　精密分光推進室
〒679-5198　兵庫県佐用郡佐用町光都1-1-1
TEL : 0791-58-0802　ext 3856
e-mail : uchiyama@spring8.or.jp