Volume 22, No.3 Pages 227 - 232
1. 最近の研究から/FROM LATEST RESEARCH
専用ビームラインの研究から ~BL15XU(物質・材料研究機構)~
直線偏光制御を用いた硬X線光電子分光による極性GaN結晶の電子状態研究
Investigating Crystalline-Polarity-Dependent Electronic Structures of GaN by Hard X-ray Photoemission using Linearly Polarized X-rays
[1](国)物質・材料研究機構 機能性材料研究拠点 Research Center for Functional Materials, National Institute for Materials Science、[2](国)物質・材料研究機構 先端材料解析研究拠点 Research Center for Advanced Measurement and Characterization, National Institute for Materials Science、[3](公財)高輝度光科学研究センター 利用研究促進部門 Research & Utilization Division, JASRI
- Abstract
- 省エネルギー社会の実現、高効率電子デバイスや発光デバイスの創成を目指し、基礎的な物性評価・良質な結晶成長・精緻な界面制御を協奏的に利用する研究開発が加速度的に進んでいる。特に、ワイドギャップ窒化物半導体である窒化ガリウム(GaN)を中心に、実用化への材料開発と基礎物性が評価されてきた。GaNは結晶由来の自発分極を有しており、その半導体特性への影響の重要性は認識されてきたが、自発分極に関連する詳細な電子状態は未解明であった。本研究では、GaNについて軌道分解した電子構造を解明するために、BL15XUにて測定した直線偏光制御硬X線光電子分光と密度汎関数法による解析を行った結果、光電子分光で観測されてきた極性に依存する価電子帯スペクトル形状の差異はpz軌道の電子の振る舞いに由来することを明らかにした。
1. はじめに
窒化ガリウム(GaN)を用いた青色発光ダイオードの発明は、2014年にノーベル物理学賞が与えられたことは周知である。今日においても、GaNはその光・電子機能に加えて、パワー半導体としても潜在的魅力にも溢れており、パワー素子への研究が活発化している。GaNはウルツ鉱型構造を有する結晶であり、c軸方向に沿ってGa面とN面が交互に積層している(図1)。その結果、c軸方向に自発分極があらわれ、圧電性や焦電性を示す。一方、(0001)-Ga極性面(以下、Ga面)や(0001)-N極性面(以下、N面)といった極性を示す点は、表面構造や結晶品質、さらには接合デバイスの特性を左右する原因となることが知られており[1,2][1] O. Ambacher, J. Smart, J. R. Shealy, N. G. Weimann, K. Chu, M. Murphy, W. J. Schaff, L. F. Eastman, R. Dimitrov, L. Wittmer, M. Stutzmann, W. Rieger and J. Hilsenbeck: J. Appl. Phys. 85 (1999) 3222.
[2] S. Nakamura: Science 14 (1998) 956-961.、解決すべき課題として残されているのが現状である。言い換えれば、極性を適切に判定し、その性質を精緻に理解することができれば、GaNを含む極性半導体の物性向上やデバイス応用への指導原理を得ることが可能となると考えられる。
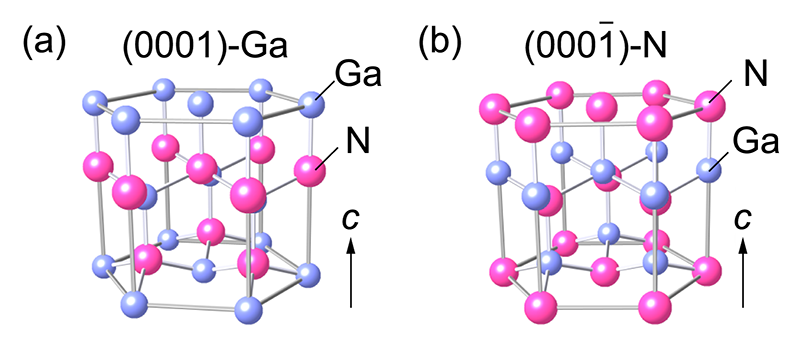
図1 ウルツ鉱型GaNの結晶構造。(a) (0001)-Ga極性、(b) (0001)-N極性。
これまでにGaNの極性判定に用いられてきた手法として、イオン散乱分光法や収束電子線回折が挙げられる。いずれの手法においても試料へダメージが与えられ、他の測定に使用することは困難である。
当グループは、GaNと同じ結晶構造を有する酸化亜鉛(ZnO)を中心に、透明酸化物導電体研究の一環として、固体内部の電子構造を直接観測できる硬X線光電子分光(HAXPES)測定に注力していた。その際に、価電子帯スペクトルに明瞭な極性依存性を見出した[3][3] N. Ohashi, Y. Adachi, T. Ohsawa, K. Matsumoto, I. Sakaguchi, H. Haneda, S. Ueda, H. Yoshikawa and K. Kobayashi: Appl. Phys. Lett. 94 (2009) 122102.。詳細に測定を進めたところ、これらの結果はc軸方向の極性が起源であることを報告した[4][4] J. Williams, H. Yoshikawa, S. Ueda, Y. Yamashita, K. Kobayashi, Y. Adachi, H. Haneda, T. Ohgaki, H. Miyazaki, T. Ishigaki and N. Ohashi: Appl. Phys. Lett. 100 (2012) 051902.。この結果は、HAXPES測定が非破壊に極性を判定する手法となることを意味している。近年では、HAXPESによる極性判定法が窒化物半導体へ波及し、それらの報告が相次いでいる[5-7][5] T. Ohsawa, S. Ueda, M. Suzuki, Y. Tateyama, J. R. Williams and N. Ohashi: Appl. Phys. Lett. 107 (2015) 171604. and references therein.
[6] D. Skuridina, D. V. Dinh, B. Lacroix, P. Ruterana, M. Hoffmann, Z. Sitar, M. Pristovsek, M. Kneissl and P. Vogt: J. Appl. Phys. 114 (2013) 173503.
[7] D. V. Dinh, D. Skuridina, S. Solopow, M. Frentrup, M. Pristovsek, P. Vogt, M. Kneissl, F. Ivaldi, S. Kret and A. Szczepańska: J. Appl. Phys. 112 (2012) 013530.。本研究では、研究を加速させる上で、我々は硬X線の偏光方向(電場ベクトル)に対して光電子強度が強い軌道依存性を示すという特徴を活用し、GaN結晶の価電子帯スペクトルの偏光依存性を検証した。さらに、密度汎関数法(DFT)によって導出したバルクGaNの電子構造と比較し、極性に依存するGaN電子構造を調べた研究について紹介する。詳細は、原著論文[5][5] T. Ohsawa, S. Ueda, M. Suzuki, Y. Tateyama, J. R. Williams and N. Ohashi: Appl. Phys. Lett. 107 (2015) 171604. and references therein.を参照されたい。
2. 硬X線光電子分光測定における直線偏光依存性
近年、硬X線の直線偏光制御を利用した固体電子構造研究が進歩している[8,9][8] A. Sekiyama, J. Yamaguchi, A. Higashiya, M. Obara, H. Sugiyama, M. Y. Kimura, S. Suga, S. Imada, I. A. Nekrasov and M. Yabashi: New Journal of Physics 12 (2010) 043045.
[9] A. Sekiyama, A. Higashiya and S. Imada: J. Electron. Spectrosc. Relat. Phenom. 190 (2013) 201-204.。ダイヤモンド移相子を適切な角度で設置し、アンジュレータ放射される水平直線偏光(以下、水平偏光)の硬X線を垂直直線偏光(以下、垂直偏光)へと変換することができる。光電子スペクトル形状が水平偏光と垂直偏光の間で著しく変化する偏光依存性を示すことが特徴である。これは励起する軌道の電子の対称性によって、光イオン化断面積(σ)がX線の偏光によって異なるためであり、これを活用することで、軌道分解した電子構造を議論できるようになった。
これまでにも、光電子スペクトルにおいて特定の電子軌道を強調する手法として共鳴光電子分光などの手段が用いられてきているが、真空紫外光や軟X線領域での測定に限られている。また、σにはX線の波長(エネルギー)依存性があるため、特定の電子軌道を強調できるが、X線の波長の変更は分析深さを変化させてしまう。本稿で注目する偏光依存性は、分析深さを変えることなく、各電子軌道の特徴を議論できる点において、これまでの手法と異なることが特長である。
3. 実験
実験はBL15XUにて実施した。光学ハッチ内に設置されている高分解能チャネルカット結晶を新たに設計・導入することで、Si111、311、333、444、555反射を利用できるように変更した。高分解能電子分析器(VG-Scienta R4000)と組み合わせることで、2.3~10.0 keVまでのX線を用いた高分解能HAXPES測定が可能となっている。図2(a)に測定の構成を示す。分光器と光源入射方向が89º(ノーマルエミッション配置)であり、光電子の検出効率を稼ぐ配置となっている。直線偏光制御については、以下の通りである。BL15XUでのHAXPES実験では主に6 keVの硬X線が用いられることを考慮して、ダイヤモンド結晶には(110)面で厚さ0.1 mmのものを用いた。詳細は省略するが、ほぼ完全なπ偏光(水平偏光)をσ偏光(垂直偏光)へ変換した際の直線偏光度は0.69で、透過率は約0.65であった。図2(b)、(c)に水平偏光と垂直偏光測定での概略図を示す。水平偏光では、電場ベクトル(![]() )と光電子脱出ベクトル(
)と光電子脱出ベクトル(![]() )が平行であるのに対して、垂直偏光では垂直となっている。試料は極性GaN結晶のGa面とN面を測定した。励起エネルギーは6 keVとし、測定は室温で行った。Au薄膜のフェルミ・カットオフから評価するエネルギー分解能は150 meVであった。
)が平行であるのに対して、垂直偏光では垂直となっている。試料は極性GaN結晶のGa面とN面を測定した。励起エネルギーは6 keVとし、測定は室温で行った。Au薄膜のフェルミ・カットオフから評価するエネルギー分解能は150 meVであった。
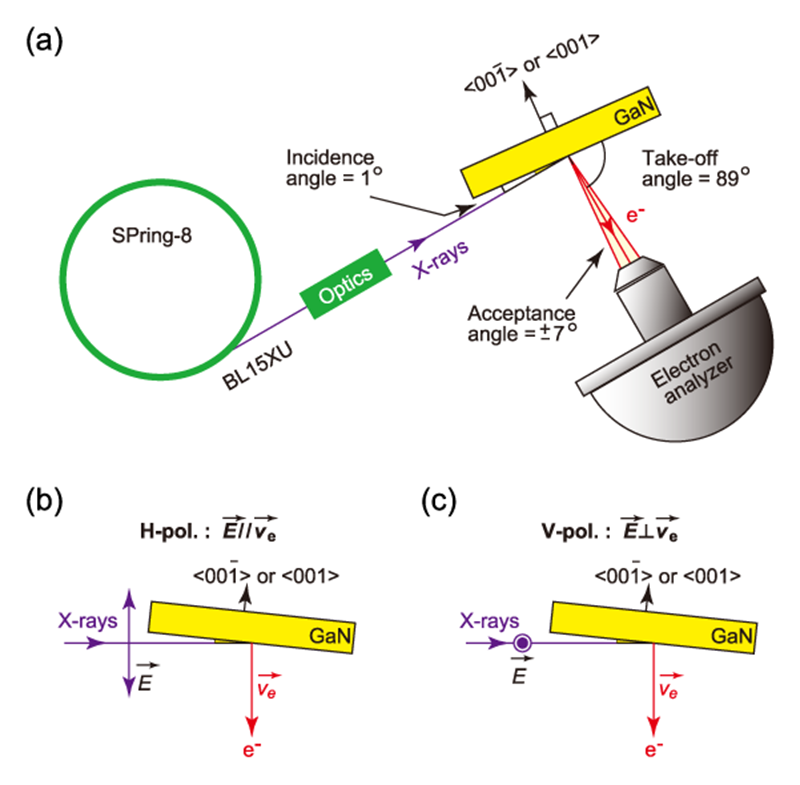
図2 硬X線光電子分光測定の概念図。(a) 全体像、(b) 水平偏光(H-pol.)、(c) 垂直偏光(V-pol.)。
実験データを深く理解するために、計算のアプローチも行った。DFTでの電子状態計算から、バルクGaNの投影状態密度(PDOS)および全状態密度を算出し、実験との比較を行った。汎関数としてGGA法[10][10] J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke: Phys. Rev. Lett. 100 (2008) 136406.やLDA法[11][11] J. P. Perdew and A. Zunger: Phys. Rev. B 23 (1981) 5048-5079.を用いた計算では、価電子帯バンド幅が過小評価されてしまったため、sX-LDA[12][12] R. Asahi, W. Mannstadt and A. Freeman: Phys. Rev. B 59 (1999) 7486-7492.やHSE06[13][13] J. Heyd, G. E. Scuseria and M. Ernzerhof: Journal of Chemical Physics 118 (2003) 8207.などの汎関数を用いることで、実験スペクトルに近い価電子帯バンド幅が得られることを確認し、本研究ではsX-LDAを採用した[5][5] T. Ohsawa, S. Ueda, M. Suzuki, Y. Tateyama, J. R. Williams and N. Ohashi: Appl. Phys. Lett. 107 (2015) 171604. and references therein.。極性結晶であることから、電子状態計算を実行する際の表面終端に課題があるため、本研究では、表面電子状態ではなく、バルクの電子状態を計算した結果に基づいて光電子分光スペクトルを再現した。
4. 極性GaN結晶の直線偏光制御硬X線光電子分光
直線偏光制御した硬X線を用いてGaN試料を測定したところ、価電子帯スペクトルの形状がGa面とN面で大きく異なることが分かった。図3(a)に、Ga面(上段)とN面(下段)の両者について測定したGaNの価電子帯HAXPESスペクトルを示す。図中のE(H)とE(V)はそれぞれ水平偏光スペクトルと垂直偏光スペクトルを示している。これらのスペクトルは直線偏光度で補正している。偏光依存性を議論する前に、E(H)で観測される極性依存性について述べる。図3(a)にて、P1ピーク強度に注目すると、Ga面(カチオン面)での強度が相対的に大きいことが分かる。この点は、ZnOや窒化インジウム試料においても同様に観測され、ウルツ鉱型結晶の極性表面に共通する特徴である[3,4,6][3] N. Ohashi, Y. Adachi, T. Ohsawa, K. Matsumoto, I. Sakaguchi, H. Haneda, S. Ueda, H. Yoshikawa and K. Kobayashi: Appl. Phys. Lett. 94 (2009) 122102.
[4] J. Williams, H. Yoshikawa, S. Ueda, Y. Yamashita, K. Kobayashi, Y. Adachi, H. Haneda, T. Ohgaki, H. Miyazaki, T. Ishigaki and N. Ohashi: Appl. Phys. Lett. 100 (2012) 051902.
[6] D. Skuridina, D. V. Dinh, B. Lacroix, P. Ruterana, M. Hoffmann, Z. Sitar, M. Pristovsek, M. Kneissl and P. Vogt: J. Appl. Phys. 114 (2013) 173503.。さらに、ここで示したGa面でのP1強度の増大は、(0001)面に対するノーマルエミッション配置で増大すると捉えるよりも、Ga面と直交する<![]() >ベクトルが分光器と平行となる試料配置が本質であることが、これまでの検討で分かっている[4][4] J. Williams, H. Yoshikawa, S. Ueda, Y. Yamashita, K. Kobayashi, Y. Adachi, H. Haneda, T. Ohgaki, H. Miyazaki, T. Ishigaki and N. Ohashi: Appl. Phys. Lett. 100 (2012) 051902.。
>ベクトルが分光器と平行となる試料配置が本質であることが、これまでの検討で分かっている[4][4] J. Williams, H. Yoshikawa, S. Ueda, Y. Yamashita, K. Kobayashi, Y. Adachi, H. Haneda, T. Ohgaki, H. Miyazaki, T. Ishigaki and N. Ohashi: Appl. Phys. Lett. 100 (2012) 051902.。
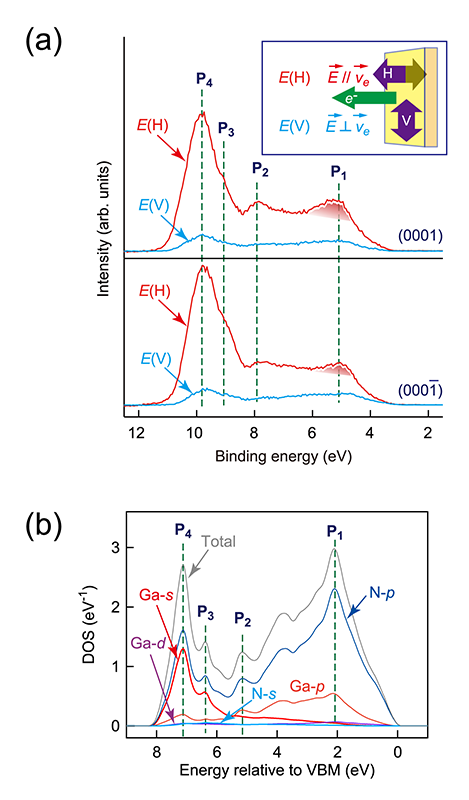
図3 (a) Ga面とN面について測定したGaN価電子帯スペクトルの偏光依存性。(b) DFT計算で導出したバルクGaNの投影状態密度。
次に、偏光依存性について議論する。E(H)とE(V)の間で大きく異なる点は、極性面に依らず、E(V)ではスペクトル全体の強度が減少することである。また、E(H)ではP4の相対強度が高いが、E(V)ではP1とP4の強度はほぼ同じとなっている。興味深いことに、E(H)で観測された極性依存性がE(V)では観測されていない。こうした定性的な理解の妥当性について、以下では、DFT計算結果と比較して、半定量的に検討した。
DFT計算から導出したバルクGaNのPDOSを図3(b)に示す。計算結果は、定性的にはsp3混成軌道に近い結合状態で説明される。価電子帯の下部には、Ga 4sやGa 4pおよびN 2pとの結合性軌道が形成され、価電子帯の上部には、Ga 4pとN 2pとの反結合性軌道が形成されていると見ることができる。
次に、実験と計算を比較する。先に述べた通り、sX-LDA汎関数を用いたことで、計算した価電子帯のバンド幅と、価電子帯スペクトルの幅がほぼ一致しており、価電子帯スペクトルとDOSとの定量的な比較が可能であると考えられる。実際、実験スペクトルで見られるP1-P4に対応したDOSの極大が存在しており、そのエネルギー位置もよく対応している。
PDOSとの比較から、偏光依存性について考察する。まず、P3とP4のDOSは、上述の通り、Ga 4s軌道とN 2p軌道が支配的となっている。表1に示したσ値[5][5] T. Ohsawa, S. Ueda, M. Suzuki, Y. Tateyama, J. R. Williams and N. Ohashi: Appl. Phys. Lett. 107 (2015) 171604. and references therein.を見ると、E(V)とE(H)との間で最も顕著な差が見られるのが、s軌道のσ値であるため、Ga 4s軌道の寄与の大きなDOSは、HAXPES強度に大きな偏光依存性を示すと考えられる。実際に、実験スペクトルにおいてP3とP4の強度が、E(H)で相対的に強く、E(V)で相対的に低くなっている。そのため、PDOSと偏光依存性の測定結果から、E(H)で見られた強いP3とP4はGa 4s軌道の寄与によると帰属することができる。
表1 6 keVの励起光エネルギーを用いた測定時におけるGaN電子軌道の光イオン化断面積(σ)[5][5] T. Ohsawa, S. Ueda, M. Suzuki, Y. Tateyama, J. R. Williams and N. Ohashi: Appl. Phys. Lett. 107 (2015) 171604. and references therein.。アナライザーでの取り込み角度を含めた実験配置を考慮している。
| Cross section(σ) | |||
| Element | Orbital | E(H) | E(V) |
| N | 2s | 29.8 | 0.602 |
| 2p | 0.134 | 0.123 | |
| Ga | 4s | 99.8 | 1.03 |
| 4p | 11.5 | 2.53 | |
| 3d | 10.9 | 5.63 | |
こうした視点で価電子帯スペクトルを半定量的に議論するため、図3(b)に示したPDOSに表1のσ値を乗じて算出した計算スペクトルと実験スペクトルを比較検討した。ここでは、バルクGaNのPDOSを用いており、表面緩和などを考慮したものではないことを注意されたい。図4では、N面の価電子帯スペクトル(上段)および計算スペクトル(中段および下段)を比較する。この計算スペクトルを見ると、以下の点に注目することができる。
1. 計算と実験のスペクトルの両者にて、P1-P4が確認され、そのエネルギー位置がほぼ一致していること。
2. 計算スペクトル形状が、N面で観測された実験スペクトルをよく再現していること。
3. E(H)とE(V)での相対的なスペクトル強度差が計算スペクトルで強調されていること。
上記1については、先に述べた通り、実験スペクトルに見られたP1-P4の存在が計算スペクトルでよく再現されていることを指摘したものである。さらに、上記2で指摘するように、スペクトルの形状がよく再現されている。実際に、図4の中段にあるE(V)の計算スペクトル形状と上段にあるE(V)の実験スペクトル形状は極めてよい一致を示している。さらに、図4の下段にあるE(H)の計算スペクトルの形状と、上段にあるE(H)の実験スペクトル形状も極めてよい一致を示している。
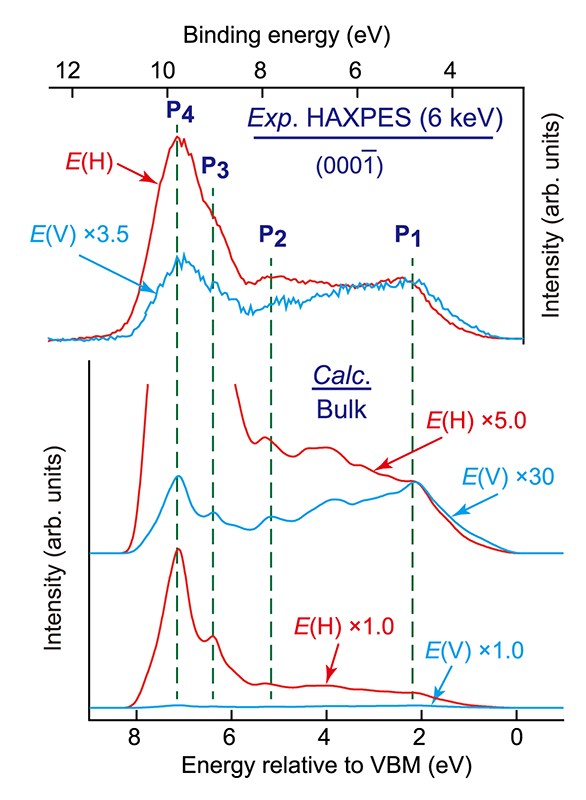
図4 硬X線実験より得られたスペクトル(上段)と計算スペクトル(中段と下段)の比較。両者がよく一致していることが分かる。
次に、偏光依存性の結果を定量的に考察する。P3とP4に顕著な偏光依存性に基づく強度の減少が見られており、これは、Ga 4s軌道のσ値減少によるものである。これに加えて、計算スペクトルの形状変化として観察される偏光依存性は、実験でのそれと類似している点が興味深い。測定した全結合エネルギー範囲で適合することから、実験のE(H)とE(V)を計算でよく再現できていることが分かった。すなわち、E(H)とE(V)のスペクトル形状を相対的には、極めてよく再現することができている。しかし、絶対強度の観点から見た場合に差異があることを指摘したのが、上記3である。E(H)とE(V)の強度差の大小はσ値の大小で説明することができる。先に述べた通り、総体的にE(V)の方でσ値が小さくなる傾向があり、実測値でも、E(V)のスペクトル強度は、E(H)に比べて小さな値となっている。しかし、定量的な視点では、実測では、E(V)とE(H)の強度差が数倍であるのに対して、計算では、数十倍の強度差になっており、現状では絶対強度の再現には至っていない。この点については、いくつかの原因が考えられる。まず、PDOSの妥当性が挙げられ、投影における曖昧さの問題が残される。一方、各軌道のσ値についても、さらなる検証の余地がある。一方で、実験でも分光器のスリット幅などの補正項を取り込んではいるがその完全性についての検証も必要である。
最後に、P1に出現する極性依存性について述べる。まず、価電子帯でP1に対応するエネルギーでのバンドを抜き出し、その電子軌道を描画すると、それがN 2pzとGa 4pzを主成分とする軌道であることが分かる。したがって、この結晶のc軸方向に伸びる電子状態が、P1に見られる結晶方位依存性に寄与していると見なすことができる。計算スペクトルはN面の実験結果と一致しているため、Ga面のP1の強度増大を説明するには、他の要因を考える必要がある。![]() と
と![]() が極性ウルツ鉱型結晶の<
が極性ウルツ鉱型結晶の<![]() >に平行であるときに限ってP1が観測される実験事実とP1はp軌道が支配的とする計算事実を考慮すると、pz軌道中の電子とウルツ鉱型格子の自発分極が相互作用する結果として、P1が顕著となっていることが示唆される。つまり、P1はGaN格子のpz軌道電子の自発分極が強く関連する光電子放出現象であると考えて、現在考察を進めている。
>に平行であるときに限ってP1が観測される実験事実とP1はp軌道が支配的とする計算事実を考慮すると、pz軌道中の電子とウルツ鉱型格子の自発分極が相互作用する結果として、P1が顕著となっていることが示唆される。つまり、P1はGaN格子のpz軌道電子の自発分極が強く関連する光電子放出現象であると考えて、現在考察を進めている。
5. まとめ
本稿では、ウルツ鉱型GaN結晶の価電子帯スペクトルに観測される極性依存性の起源を解明するために、我々が取り組んだ直線偏光制御HAXPES測定について紹介した。HAXPESのバルク敏感性に、直線偏光制御という利点を加えることによって、GaN価電子帯の電子構造についての新たな知見を得ることに成功した。また、最新のPDOS結果や実験配置を考慮した光イオン化断面積値を用いた計算アプローチと共に検証することによって、極性依存性の起源を明らかにすることができるようになりつつある。
謝辞
本研究は、SPring-8内のBL15XUにて実施した(課題番号2010B4607、2011A4610、2011B4610、2012A4603、2012A4612、2012B4612、2013A4716)。本研究は、東工大元素戦略拠点の支援を受けた。
参考文献
[1] O. Ambacher, J. Smart, J. R. Shealy, N. G. Weimann, K. Chu, M. Murphy, W. J. Schaff, L. F. Eastman, R. Dimitrov, L. Wittmer, M. Stutzmann, W. Rieger and J. Hilsenbeck: J. Appl. Phys. 85 (1999) 3222.
[2] S. Nakamura: Science 14 (1998) 956-961.
[3] N. Ohashi, Y. Adachi, T. Ohsawa, K. Matsumoto, I. Sakaguchi, H. Haneda, S. Ueda, H. Yoshikawa and K. Kobayashi: Appl. Phys. Lett. 94 (2009) 122102.
[4] J. Williams, H. Yoshikawa, S. Ueda, Y. Yamashita, K. Kobayashi, Y. Adachi, H. Haneda, T. Ohgaki, H. Miyazaki, T. Ishigaki and N. Ohashi: Appl. Phys. Lett. 100 (2012) 051902.
[5] T. Ohsawa, S. Ueda, M. Suzuki, Y. Tateyama, J. R. Williams and N. Ohashi: Appl. Phys. Lett. 107 (2015) 171604. and references therein.
[6] D. Skuridina, D. V. Dinh, B. Lacroix, P. Ruterana, M. Hoffmann, Z. Sitar, M. Pristovsek, M. Kneissl and P. Vogt: J. Appl. Phys. 114 (2013) 173503.
[7] D. V. Dinh, D. Skuridina, S. Solopow, M. Frentrup, M. Pristovsek, P. Vogt, M. Kneissl, F. Ivaldi, S. Kret and A. Szczepańska: J. Appl. Phys. 112 (2012) 013530.
[8] A. Sekiyama, J. Yamaguchi, A. Higashiya, M. Obara, H. Sugiyama, M. Y. Kimura, S. Suga, S. Imada, I. A. Nekrasov and M. Yabashi: New Journal of Physics 12 (2010) 043045.
[9] A. Sekiyama, A. Higashiya and S. Imada: J. Electron. Spectrosc. Relat. Phenom. 190 (2013) 201-204.
[10] J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke: Phys. Rev. Lett. 100 (2008) 136406.
[11] J. P. Perdew and A. Zunger: Phys. Rev. B 23 (1981) 5048-5079.
[12] R. Asahi, W. Mannstadt and A. Freeman: Phys. Rev. B 59 (1999) 7486-7492.
[13] J. Heyd, G. E. Scuseria and M. Ernzerhof: Journal of Chemical Physics 118 (2003) 8207.
(国)物質・材料研究機構 機能性材料研究拠点
〒305-0044 茨城県つくば市並木1-1
TEL : 029-860-4806
e-mail : ohsawa.takeo@nims.go.jp
(国)物質・材料研究機構 機能性材料研究拠点
〒305-0044 茨城県つくば市並木1-1
TEL : 029-860-4867
e-mail : ohashi.naoki@nims.go.jp
(国)物質・材料研究機構 先端材料解析研究拠点
〒679-5148 兵庫県佐用郡佐用町光都1-1-1
TEL : 0791-58-0802 ext 3955
e-mail : ueda.shigenori@nims.go.jp
(公財)高輝度光科学研究センター 利用研究促進部門
〒679-5198 兵庫県佐用郡佐用町光都1-1-1
TEL : 0791-58-2750
e-mail : m-suzuki@spring8.or.jp
BL15XUでの実験を検討されている方は、BL15XUの公式HPをご覧ください。
BL15XU website:http://www.nims.go.jp/webram/
「ステーション概要」ではBL15XUで利用可能な装置の情報を、「装置を使いたい方へ」では、課題募集の手続き手順や必要書類の情報を記載しています。
利用に関するご相談はBL15XUスタッフまたはオフィス(BL15XUoffice@ml.nims.go.jp)にて随時受け付けています。








