Volume 21, No.2 Pages 78 - 83
1. 最近の研究から/FROM LATEST RESEARCH
短パルスX線回折による水晶の振動機構の解明
Oscillation Mechanism of Quartz Crystal Clarified by Short Pulse X-ray Diffraction
[1]名古屋市立大学 大学院システム自然科学研究科 Graduate School of Natural Sciences, Nagoya City University、[2](公財)高輝度光科学研究センター 利用研究促進部門 Research & Utilization Division, JASRI、[3]広島大学 大学院理学研究科 Graduate School of Science, Hiroshima University
- Abstract
- 水晶は、時計をはじめとする多種多様な電子機器の基準信号を発振する振動子として広く利用されているが、その振動機構は長い間不明であった。SPring-8の短パルスX線を用いた交流電場下X線回折実験により、交流電場と共振している水晶振動子の高速かつ微小な原子の運動を追跡して観測することに成功した。直流電場に対する水晶の逆圧電効果による格子歪みは極めて小さいが、共振周波数の交流電場下では格子歪みが1万倍程度に増幅された。この大きな格子歪みに反して結晶構造を形成するSiO4四面体に変形は全く見られず、SiO4四面体をつなぐSi−O−Si結合角にのみ変形が見られた。水晶振動子の安定した圧電振動は、強固なSiO4四面体をつなぐSi−O−Si結合角の弾性的な変形と復元によって引き起こされることが分かった。
1. はじめに
水晶(石英、α-SiO2)は、地球上に豊富に産出する天然鉱物としてよく知られているが、圧電性を有すると同時に安定した周波数で振動することから、現在、時計をはじめとする多種多様な電子機器の基準信号を発振する振動子として、広く産業利用されている。圧電性とは、応力に対して電気分極を発生し、電場に対して歪みを発生する性質である。いわゆる水晶時計は、毎秒32,768(= 215)回振動する水晶振動子を用いることで、正確に時を刻む。水晶は現代社会を支える基幹材料の一つと言えるが、一方で水晶がどのようにして安定した周波数の電気信号を発振できるのか、その詳しい振動機構は長い間不明であった。
古くより水晶の圧電性は、Si4+陽イオンとO2−陰イオンが印加した電場に対して互いに逆方向に変位することにより、電気分極と同時に歪みを発生することで説明され続けてきた[1,2][1] W. H. Bragg and R. E. Gibbs: Proc. R. Soc. Lond. A 109 (1925) 405-427.
[2] A. Meissner: Z. Tech. Phys. 8 (1927) 74-77.。しかし、Si原子とO原子は共有結合によって結合しているため、電場に対して自由に動くことはできない。また一般的な水晶振動子で利用されている厚みすべり変形では、図1aに示すように電場Eに対して垂直にずり歪みsが発生するため、電場に平行なイオンの変位だけで説明することはできない。
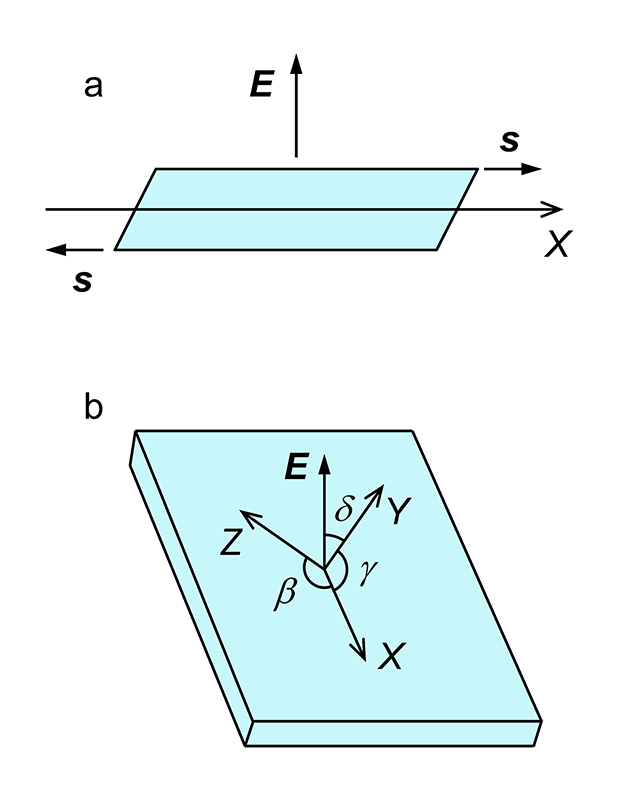
図1 ATカット水晶振動子の厚みすべり変形(a)と、結晶方位(b)。
水晶の振動機構を理解するには、振動している水晶内の原子の運動を直接観測する必要がある。しかし、水晶内の原子の運動は極めて高速かつ微小であるため、直接観測するのは難しい。一般に使われている水晶振動子の発振周波数は、kHz~MHzである。また、水晶の圧電定数d(d = s/E)は小さく、1 kV/mmの大きな電場Eを加えたとしても、歪みsは~10−6程度にしかならない。水晶の圧電変形機構を理解するために、これまでに数kV/mmの直流電場下でのX線回折実験が行われているが、それによって検出された構造変化は微々たるもので、実験誤差を有意に上回るものではなかった[3-5][3] U. Pietsch, J. Stahn, J. Davaasambuu and A. Pucher: J. Phys. Chem. Solids 62 (2001) 2129-2133.
[4] J. Davaasambuu, A. Pucher, V. Kochin and U. Pietsch: Europhys. Lett. 62 (2003) 834-840.
[5] R. Guillot, P. Fertey, N. K. Hansen, P. Allé, E. Elkaïm and C. Lecomte: Eur. Phys. J. B 42 (2004) 373-380.。
水晶振動子の高速かつ微小な原子の運動を観測するために、本研究[6][6] S. Aoyagi, H. Osawa, K. Sugimoto, A. Fujiwara, S. Takeda, C. Moriyoshi, Y. Kuroiwa: Appl. Phys. Lett. 107 (2015) 201905-1-5.ではSPring-8の高輝度短パルスX線と、交流電場との共振現象を利用した。SPring-8から放射されるパルス長~50 psの短パルスX線は、MHz領域での原子の運動の追跡を可能にする。また、交流電場との共振効果を利用することで、水晶振動子の微小な原子変位を大きく増幅させて精度よく検出できる。
2. ATカット水晶振動子
測定に用いた試料は、市販のATカット水晶振動子である。水晶には互いに鏡像関係にある右水晶(空間群P 3221)と左水晶(空間群P 3121)があるが、工業的に用いられる水晶はすべて右水晶である。右水晶の2回回転軸をX軸、3回らせん軸をZ軸、XZ面に垂直な方向をY軸とすると、ATカットではY軸からZ軸にδ~35°傾けた方向に垂直に結晶を切り出す(図1b)。ATカット水晶振動子は、室温付近での発振周波数の温度変化が小さいことから、工業的に広く用いられる。
ATカット水晶振動子は、印加された電場Eに対してX軸とY軸のなす角γと、X軸とZ軸のなす角βが変化することで厚みすべり変形を起こす(図1b)。それぞれの90°からの変化量Δγ、Δβは、圧電定数d11 = −2.31 pm/V、d14 = −0.727 pm/Vを用いて[7][7] R. Bechmann: Phys. Rev. 110 (1958) 1060-1061.、
| tan Δγ = 2Ed11cos δ | (1) |
| tan Δβ = Ed14cos δ | (2) |
で与えられる。E = 1 kV/mmのとき、Δγ = 2.2 × 10−4°、Δβ = 3.4 × 10−5°と計算される。
圧電振動子の発振周波数は、形状と密度、弾性定数によって決まる。ATカット水晶振動子の厚みすべり振動の発振周波数f0(MHz)は、振動子の厚みh(µm)を用いて、
| f0 = 1,664/h | (3) |
で与えられる[8][8] R. M. Cerda: Understanding Quartz Crystals and Oscillators (Artech House, Norwood, MA, USA, 2014).。X線回折により結晶構造を精密に求めるためには、X線の吸収効果、消衰効果の少ないなるべく厚みの薄い試料を用いる必要がある。本研究では、h = 55 µm、f0 = 30 MHzのATカット水晶振動子を実験に用いた。
3. 直流電場下X線回折
X線回折実験は、SPring-8 BL02B1の大型湾曲イメージングプレート(IP)カメラを用いて行った。BL02B1の大型湾曲IPカメラは広い角度範囲の多数のブラッグ反射を効率よく短時間で測定することができる。入射X線の波長は0.41 Åとした。
交流電場下での測定を行う前に、まず直流電場に対する構造変化の検出を試みた。ATカット水晶振動子に直流電場を印加した状態でX線振動写真を撮影した。得られたX線回折データから、格子定数および結晶構造を求めた。水晶は三方晶系に属し、その格子定数は、a = 4.91 Å、c = 5.40 Åであるが、本稿ではX、Y、Z軸を主軸にとったC底心の直方晶系の単位格子(a = 4.91 Å、b = 8.50 Å、c = 5.40 Å、α = β = γ = 90°)を用いる。印加した直流電場の最大値は±40 kV/mmである。これより大きな直流電場の印加は、放電が起こるため不可能であった。
数百点のブラッグ反射位置から最小二乗法により求めた格子定数β、γの変化量Δβ、Δγの直流電場に対する変化を図2に示す。Δβ、Δγは直流電場Eに対してほぼ線形に変化した。図2から(1)、(2)式を用いて圧電定数を見積もると、d11 = −2.3 pm/V、d14 = −0.9 pm/Vとなり、ほぼバルク測定の結果[7][7] R. Bechmann: Phys. Rev. 110 (1958) 1060-1061.と一致した。
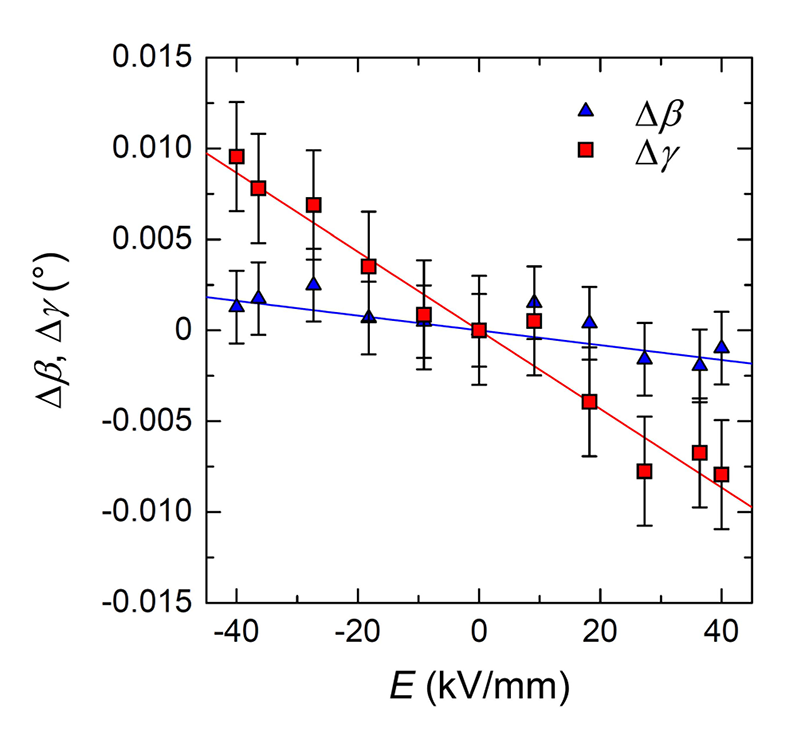
図2 ATカット水晶振動子のΔβ、Δγの直流電場に対する変化。
直流電場E = +36および、−36 kV/mm下での結晶構造を、4千点以上のブラッグ反射強度から最小二乗法により求めた。両者のγ角の違いは0.015°、β角の違いは0.004°とごく僅かである(図2)。結晶構造解析の結果、Si−O結合距離(~1.61 Å)、O−Si−O結合角(~109°)、Si−O−Si結合角(~143°)について、実験誤差(結合距離については0.1 pm、結合角については0.1°)を上回る違いは観測されなかった。
4. 交流電場下時分割X線回折
発振周波数f0と同じ周波数の交流電場を印加すると、共振効果により歪みを増幅できる。周波数f = f0 = 30 MHz、電場振幅E0 = 0.18 kV/mmの正弦波交流電場を印加したATカット水晶振動子に対して、短パルスX線を用いた時分割X線回折実験を行った。
SPring-8では、セベラルバンチ運転により、単電子バンチから放射されるパルス幅~50 psの短パルスX線を利用できる。SPring-8のセベラルバンチ運転の運転モードには、AからHまで8種類がある。Hモードは単電子バンチの蓄積電流が最も大きく、全蓄積電流100 mAのうち5 mAが単電子バンチとして周回運動する。本実験ではHモードの単電子バンチから放射される短パルスX線を、実験ハッチ内に設置したX線チョッパーを用いて26 kHzの繰り返し周波数(蓄積リング8周に1回の周期)で取り出して試料に照射した。このときの入射X線の強度は、X線チョッパーを使わない場合に比べると、(5 mA/100 mA) × (1周/8周) = 1/160程度である。
時分割X線回折実験をするためには、試料の振動周期(30 MHz)と短パルスX線の繰り返し周期(26 kHz)を正確に同期させる必要がある。しかし、水晶振動子の共振現象は非常に狭い限られた振動数領域でしか起きないため、試料の振動周期を自由に変更することはできない。また、電子バンチの周回周期は電子エネルギーと蓄積リングの周長で決まっているため、短パルスX線の繰り返し周期を自由に変更することもできない。この問題を解決するために本実験では、周波数f = 30 MHz付近の正弦波1,000周期分(33 ns × 1,000 = 33 µs)に待機時間(5 µs)を加えた38 µsを1周期とする交流電場を、26 kHz(= 1/38 µs)で繰り返して試料に印加することにした(図3)。このとき断続的に交流電場を印加することになるため、試料の振動の減衰や位相のずれに注意しなければならないが、水晶では共振が減衰することなく継続し、大きな問題にならなかった。
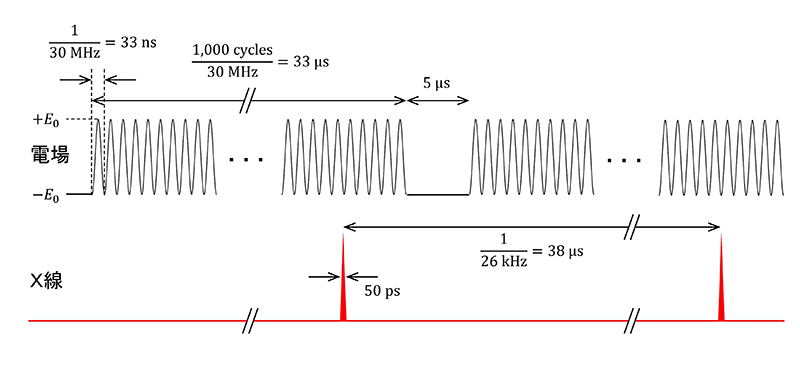
図3 印加した交流電場の時間構造(上)と短パルスX線(下)との関係。
この交流電場に同期した短パルスX線を26 kHzの周波数で繰り返し試料に入射することで、その瞬間のX線回折パターンをIPカメラで測定した。結晶の向きを変えて複数のX線振動写真を撮影することで、瞬間の結晶構造を決定するのに十分な数のブラッグ反射を測定した。上述したとおりX線チョッパーの使用により入射X線強度が通常の1/160程度になっているが、水晶はX線回折強度が強いため、振動角度1°あたり90秒程度の露光時間で結晶構造解析に必要なX線回折データを測定することができた。X線パルスに対する交流電場の遅延時間Δtを変化させることで、共振中のX線回折パターンの時間変化を計測した。印加した正弦波交流電場1,000周期のうち、およそ995周期目の1周期分(33 ns)に対して測定を行った(図3)。得られたX線回折データから、格子定数および結晶構造の時間変化を求めた。
5. 水晶振動子の原子ダイナミクス
数百点のブラッグ反射位置から最小二乗法により求めたΔγ、Δβの交流電場下の時間変化を図4aに示す。周波数f = f0 = 30 MHzで正弦波状に振動する大きな変形が観測された。γ、β以外の格子定数にはこのような時間変化は観測されなかった。図4a中のΔγ、Δβの最大値は、印加する交流電場の電場振幅E0に対して線形に変化した。E0 = 0.18 kV/mmのとき、Δγ、Δβの最大値は、それぞれ0.15°、0.10°である。直流電場の場合、E = 0.18 kV/mmのとき(1)、(2)式よりΔγ = 4 × 10−5°、Δβ = 6 × 10−6°と計算される。従って、格子歪みは交流電場との共振効果により、Δγで4千倍、Δβで1万倍以上に増幅されたことになる。実験機器の制約上、E0を0.18 kV/mmより大きくすることはできないが、それでもΔγ、Δβの最大値は、図2の直流電場下の実験に比べて数十倍大きい。この大きな格子歪みに伴って、図4bに示すように、ブラッグ反射強度にも格子歪みと同期した時間変化が観測された。単位格子中の原子位置は、ブラッグ反射強度から求められる。従って、これなら振動中の原子変位を観測できるはずである。
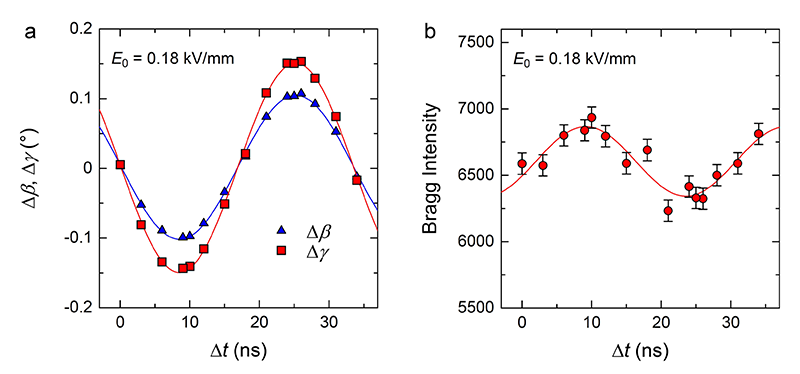
図4 ATカット水晶振動子の交流電場下のΔβ、Δγの時間変化(a)と、390ブラッグ反射強度の時間変化(b)。
Δγ、Δβが負および正に最大となる遅延時間Δt = 9および25 ns(図4a)での結晶構造を、3千点以上のブラッグ反射強度から最小二乗法により求めた。直流電場下での結晶構造解析の結果と同様に、Si−O結合距離、O−Si−O結合角については、実験誤差(結合距離については0.2 pm、結合角については0.1°)を上回る違いは観測されなかった。従って大きな格子歪みに反して、結晶構造を形成するSiO4四面体はほぼ変形しない。一方、SiO4四面体をつなぐSi−O−Si結合角には、明らかな変化が観測された。
Δt = 9および25 nsでのSi−O−Si結合角を表1に示す。電場下で歪んだ水晶の結晶構造は、3つの独立なSiO4四面体で構成され、独立な酸素原子を6個(O(1)~O(6))含む。Δt = 9と25 nsでのSi−O−Si結合角の違いは、O(1)、O(4)、O(5)、O(6)については実験誤差(0.1°)を少し上回る程度であるが、O(2)、O(3)については明瞭に観測された(表1)。Δt = 9から25 nsへの構造変化では、γとβがそれぞれおよそ0.3°と0.2°増大するが、そのときO(2)のSi−O−Si結合角はおよそ0.8°減少し、O(3)のSi−O−Si結合角はおよそ0.6°増大する。
| 表1 Δt = 9および25 nsでのSi−O−Si結合角 | ||
| Δt (ns) | 9 | 25 |
| Si(1)−O(1)−Si(3) (°) | 143.97(11) | 143.81(12) |
| Si(1)−O(2)−Si(3) (°) | 144.19(11) | 143.41(12) |
| Si(2)−O(3)−Si(1) (°) | 143.37(10) | 144.02(11) |
| Si(2)−O(4)−Si(1) (°) | 143.50(11) | 143.82(12) |
| Si(3)−O(5)−Si(2) (°) | 143.73(16) | 143.27(17) |
| Si(3)−O(6)−Si(2) (°) | 143.42(15) | 143.61(17) |
O(2)とO(3)のSi−O−Si結合角の大きな変形は、O原子の、電場による変位と結晶中の配置から理解できる。理論計算によれば、Si−O結合は共有結合とイオン結合の両方の性質を持ち、イオン式として水晶は(Si2.60+)(O1.30−)2と書くことができる[9][9] Y.-N. Xu and W. Y. Ching: Phys. Rev. B 51 (1995) 17379-17389.。測定したX線回折データから最大エントロピー法により電子密度分布を求め、各原子の電子数を見積もったところ、中性からの電荷のずれは、Siで+2.8 e、Oで−1.4 eであった(eは電荷素量)。古典的なモデルで提案されている通り、正、負に帯電しているSi、O原子は電場印加によって互いに逆方向に変位すると予想されるが、Si−O共有結合はその大きな妨げとなる。Si原子は、四面体配位した4つのO原子と共有結合しているため、極めて変位しにくい。O原子については、その変位方向がSi−O結合に平行なとき、大きな反発力を受ける。逆に、O原子の変位方向が2つのSi−O結合に垂直なとき(Si−O−Si面に垂直なとき)、Si−O結合距離の変化なしにO原子は比較的容易に変位することができる。O(1)~O(6)を比較すると、O(2)、O(3)が最もこの条件にあてはまる(図5)。このため、O(2)とO(3)は電場に応答して変位しやすく、Si−O−Si結合角の変形が大きくなる。
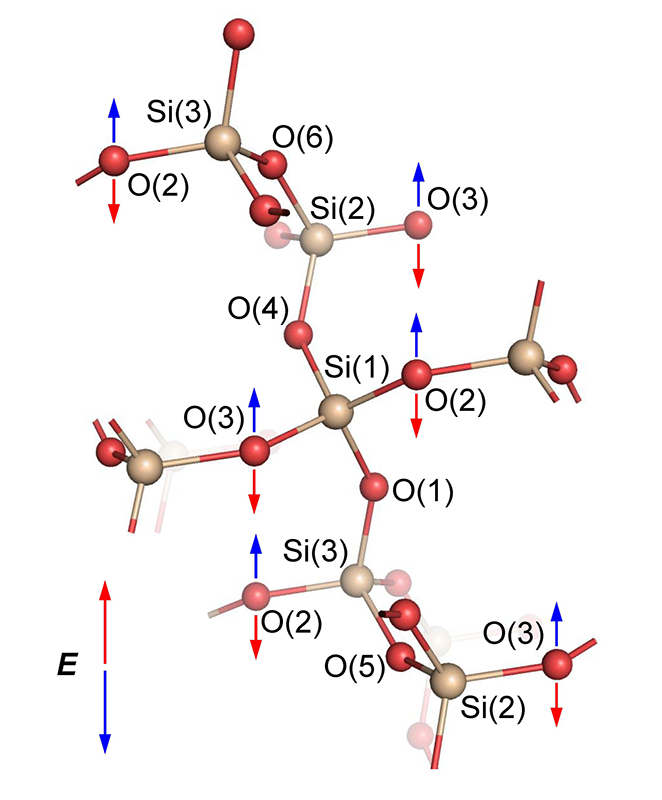
図5 X軸方向から見たATカット水晶振動子の結晶構造と電場Eに対するO(2)、O(3)の原子変位。
以上の結果から、ATカット水晶振動子の厚みすべり振動の振動機構は、次のように説明できる。構造的に独立な3個のSi原子をSi(1)、Si(2)、Si(3)とすると、Si(1)にはO(1)~O(4)が、Si(2)にはO(3)~O(6)が、Si(3)にはO(5)、O(6)、O(1)、O(2)が、四面体配位で共有結合している(図5)。このうちO(2)、O(3)は、そのSi−O結合方向から電場に対して特別変位しやすいため、電場を印加すると各SiO4四面体にトルクが発生し、3個のSiO4は交互に回転する。このときSiO4の回転による歪みは、O(2)、O(3)のSi−O−Si結合角に集中する。この歪みにより、結晶格子および結晶全体にずり歪みが発生する。Si−O−Si結合角に蓄えられた弾性エネルギーは、その復元力によりO原子の運動エネルギーに転換され、Si−O−Si結合角は直ちに元に戻ったあと逆方向に歪む。これが繰り返されることで水晶振動子は振動する。Si−O−Si結合角の変形は弾性的であり、復元の際のエネルギー損失が少ないために振動の減衰が起きにくく、共振による振動の増幅効果が特別大きいと考えられる。
6. おわりに
SPring-8の短パルスX線を用いた交流電場下X線回折実験により、30 MHzで振動しているATカット水晶振動子の原子ダイナミクスを追跡することに成功した。この成果は、SPring-8でこれまでに開発されてきた、Hモード加速器運転による高輝度短パルスX線、X線チョッパー、マルチモード高精度タイミング制御技術、大型湾曲IPカメラ等の要素技術を、複合的に利用することで初めて達成され得た。水晶振動子の正確な振動は、頂点共有した強固なSiO4四面体の同期した交互回転と、SiO4四面体をつなぐSi−O−Si結合角のエネルギー損失の少ない弾性的な変形・復元によってもたらされる。本研究で確立した実験技術は、水晶以外の圧電・強誘電材料の交流電場下の構造応答計測に応用できる。今後、同様の手法により様々な圧電・強誘電体材料の電場下の構造応答を明らかにしていくことで、圧電・強誘電現象の微視的理解が飛躍的に進むものと期待している。
謝辞
SPring-8での実験は、長期利用課題(2013B0100、2014A0100、2014B0100)の中で行われた。実験にご協力頂いた広島大学 竹田翔一氏にお礼申し上げる。本研究は、日本学術振興会科学研究費補助金(26870491)の助成のもと行われた。
参考文献
[1] W. H. Bragg and R. E. Gibbs: Proc. R. Soc. Lond. A 109 (1925) 405-427.
[2] A. Meissner: Z. Tech. Phys. 8 (1927) 74-77.
[3] U. Pietsch, J. Stahn, J. Davaasambuu and A. Pucher: J. Phys. Chem. Solids 62 (2001) 2129-2133.
[4] J. Davaasambuu, A. Pucher, V. Kochin and U. Pietsch: Europhys. Lett. 62 (2003) 834-840.
[5] R. Guillot, P. Fertey, N. K. Hansen, P. Allé, E. Elkaïm and C. Lecomte: Eur. Phys. J. B 42 (2004) 373-380.
[6] S. Aoyagi, H. Osawa, K. Sugimoto, A. Fujiwara, S. Takeda, C. Moriyoshi, Y. Kuroiwa: Appl. Phys. Lett. 107 (2015) 201905-1-5.
[7] R. Bechmann: Phys. Rev. 110 (1958) 1060-1061.
[8] R. M. Cerda: Understanding Quartz Crystals and Oscillators (Artech House, Norwood, MA, USA, 2014).
[9] Y.-N. Xu and W. Y. Ching: Phys. Rev. B 51 (1995) 17379-17389.
名古屋市立大学 大学院システム自然科学研究科
〒467-8501 愛知県名古屋市瑞穂区瑞穂町山の畑1
TEL : 052-872-5061
e-mail : aoyagi@nsc.nagoya-cu.ac.jp
(公財)高輝度光科学研究センター 利用研究促進部門
〒679-5198 兵庫県佐用郡佐用町光都1-1-1
TEL : 0791-58-2750
e-mail : hitoshio@spring8.or.jp
(公財)高輝度光科学研究センター 利用研究促進部門
〒679-5198 兵庫県佐用郡佐用町光都1-1-1
TEL : 0791-58-2750
e-mail : ksugimoto@spring8.or.jp
広島大学 大学院理学研究科
〒739-8526 広島県東広島市鏡山1-3-1
TEL : 082-424-7399
e-mail : moriyosi@sci.hiroshima-u.ac.jp
広島大学 大学院理学研究科
〒739-8526 広島県東広島市鏡山1-3-1
TEL : 082-424-7397
e-mail : kuroiwa@sci.hiroshima-u.ac.jp








