Volume 11, No.4 Pages 245 - 251
2. 最近の研究から/FROM LATEST RESEARCH
磁気コンプトンプロファイル測定による層状Mn酸化物の電子・軌道状態の研究 −二次元再構成に焦点をあてて−
Study of Electronic and Orbital States in a Bilayer Manganite −Focusing on Two−Dimensional Reconstruction of Magnetic Compton Orofiles−
1.はじめに
ペロフスカイトMn酸化物については、低温の強磁性金属(FM)相から絶縁相への転移温度Tcにおいて巨大磁気抵抗効果(CMR)を示すことが報告されたのをきっかけにして[1]、実験的にも理論的にも精力的な研究が行われてきた。従来、低温のFM状態は、二重交換相互作用によって説明されてきたが[2]、CMRを含む伝導性や、温度やホール濃度に依存した複雑な磁気構造の変化、電荷・軌道秩序等は、電荷やスピンの自由度のみでは説明できず、軌道自由度の重要性も指摘されるようになった[3]。磁性や伝導性を担うと考えられるMn-3d電子状態は、MnO6八面体の結晶場によりt2g軌道とeg軌道に分裂しているが、この系の物性を理解するためには、特に、eg軌道がどのような状態にあるかを知ることが必要であろう。放射光を利用した軌道物理の研究という点から言えば、X線共鳴散乱測定による軌道秩序の観測が良く知られていると思われるが、これは、試料中元素の吸収端エネルギーを持ったX線を利用して、軌道秩序による電子状態の空間的変調を調べるものである。我々は、これと相補的な情報を得る方法として磁気コンプトンプロファイル(MCP)測定に着目し、層状Mn酸化物における軌道占有状態を調べることを目的に特定課題の採択を受けた。その期間中には、1)MCPのホール濃度依存性、2)MCPの異方性、3)MCPの温度変化、4)TcにおけるMCPの磁場依存性、5)MCPの二次元再構成、6)高分解能コンプトンプロファイルの二次元再構成などの系統的な実験を行ってきたが[4]、本稿では、特にMCPの二次元再構成に焦点をあてて紹介する[5]。
2.MCPの特徴と測定、解析について
2-1.MCPの特徴
試料に入射されるX線のエネルギーが原子内の電子の束縛エネルギーよりも充分に高いとき、インパルス近似のもとに、磁気コンプトンプロファイル(MCP,Jmag(pz))は次のように表される[6]。
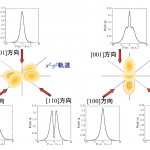
ここで、pzはX線の散乱ベクトル方向に沿った電子の運動量成分であり、χi↑(↓)(p)は運動量表示の波動関数で、添え字は始状態における上向きスピン(下向きスピン)を持ったi-番目の電子であることを表している。試料を強磁性体として、添え字の i やjで表される全ての占有状態についての和をとると、強磁性を担うスピンを持った電子のみがMCPに寄与することがわかる。従って、MCPの面積、即ち、プロファイルをpzについて積分した量は、スピン磁気モーメントの大きさに比例する。また、式(1)に示したように、MCPは、px,pyについての二重積分の形ではあるが、波動関数を直接的に反映したものとなっている。図1にx2-y2軌道と3z2-r2軌道についての例を示すが、MCPの形が磁性電子の占有する軌道によって異なること、また、同じ軌道であっても観測方向によって異なることがお分かり頂けるであろう。実験的には、各軌道のプロファイルの重ね合わせとして観測される。試料に単結晶を用い、複数の結晶方位においてMCPを測定し、それらに対して再構成の解析を行うと、二次元或いは三次元のスピン運動量密度が得られ、結果として、磁性電子の占有状態を視覚化することが可能である。このような実験は、これまで、大きな磁気効果を示すFe試料(〜2% at BL08W,SPring-8)でしか行われていなかったが[7]、近年の放射光技術の進展により、磁気効果の小さい試料(〜0.5%)でも現実的なマシンタイムの範囲内で再構成測定が可能となっている。
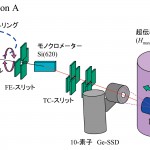
(a)測定された各方向のMCP (b)MCPの再構成解析により求められた二次元スピン運動量密度
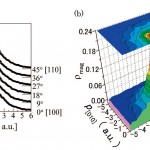
図3(a)のMCPに対してdirect Fourier変換法による二次元再構成を行い[8]、その結果として得られた二次元スピン運動量密度(2D-SMD)を図3(b)に示す。この解析の手順は次のとおりである。各方向のMCPは、一旦、Fourier変換によりr-空間の一次元関数B(r)に変換される。次に、各B(r)関数の間を補完して、二次元或いは三次元のB(r)関数を求める。このB(r)関数を逆Fourier変換して、再度、運動量空間に戻してやると、運動量密度ρ(p)が得られる。二次元再構成の場合には、運動量密度を観測面に垂直な方向について積分したρ( px , py )=∫ρ(p)dpzとなる。従って、図3(b)は、Mn-3d軌道のスピン運動量密度を(001)面に射影したものとなっている。図中で、p[100],p[010]軸に沿って2a.u.付近に見られる谷状構造や原点付近の凹は、ドープされたホールがx2-y2軌道や3z2-r2軌道に入っていることを表している。
3-1.分子軌道計算を用いた軌道占有状態の解析
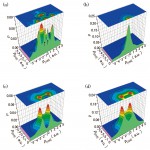
分子軌道計算から得られる波動関数を用いて計算された (a)x2-y2的分子軌道 (b)3z2-r2的分子軌道 (c)t2g的分子軌道の二次元運動量密度 (d)各分子軌道を実験にフィッティング解析した結果
次に、局所スピン密度近似に基づくバンド計算を行い、その結果から求めた2D-SMDとの比較を行った。このバンド計算には、BL08Wに導入されているBANDS01というプログラムを使用した。計算において、Sr原子をBa原子で置き換え、La/Baサイトは“56.4”の核電荷を持った仮想原子に占有されていると仮定した。また、ハーフメタル状態を求めるためにUeff =U−J =2eV とした。分子軌道計算の場合と同様に、バンド計算の結果として得られる波動関数から各方向のMCPを計算し、それらに二次元再構成の解析を施した。その結果として、図5(a)に、磁化に寄与する価電子帯の2D-SMDを示す。これを図3(b)に示した実験の2D-SMDと比べると、全体的な形は良く再現されているように見える。金属物質においては、波動関数は結晶格子の周期によるブロッホ関数で記述でき、従って、周期ポテンシャルによって決められるバンド構造が必然的に運動量密度に反映されているはずである。そこで、実験とバンド計算による両方の2D-SMDに対してLock-Crisp-West(LCW)法による解析を行い、運動量密度をk−空間における占有数密度に変換したマップを求めてみた[12]。二次元の解析の場合、占有数密度は N( kx , ky )=
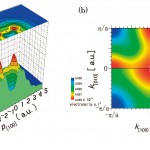
図5 バンド計算とスピン占有数密度
(a)バンド計算から得られる波動関数を用いて計算された二次元スピン運動量密度
(b)LCW解析の結果(スピン占有数密度)上半分:実験、左下半分:バンド計算、右下半分:x2-y2的分子軌道
4.おわりに
以上、層状Mn酸化物の電子・軌道状態を調べることを目的に行ったMCPの二次元再構成実験とその解析結果について述べてきた。分子軌道計算及び バンド計算から得られる波動関数を用いてMCP、2D-SMD、LCWマップを計算し、eg電子の局在性と遍歴性という観点から実験結果と比較したところ、Tc以下のFM相において、バンド的状態と局在ポーラロン状態が共存していることを示唆する結果が得られた。これは、一方向だけで測定されたMCPの解析からは得難い情報であり、再構成実験の有効性を示すものと言える。本稿では紹介できなかったが、高分解能コンプトンプロファイルの再構成実験を、FM相、Tc以上の絶縁相、更に磁場を印加したCMR条件下で行っており、各状態で電子状態が大きく変化していることも見出している。
おそらく、コンプトン散乱という現象自体については、多くの方がご存知のことと思われる。しかし、これを実験手法として用いたときに、どのような情報が得られるのかについては、案外知られていないのが実情ではないだろうか。コンプトン実験には、温度(低温 or 高温)、磁場の有無、高圧、などの測定条件について大きな制約が無い。また、試料についても、その形態(固体、液体、気体)、結晶or非結晶によらず測定可能であり、試料表面についても特段の気を使わなくても良い。測定環境さえ整えてやれば、いろいろな分野で活用可能な測定手法であると言える。本稿がコンプトン散乱実験に対する理解の一助となり、少しでも興味を持って頂けたなら幸いである。
本特定課題における研究は、以下の方々によるご協力のもとに行うことができました。ここに感謝の意を表します。坂井信彦、角谷幸信、永尾俊博、尾村朱美、河井友也、大谷幸子、小泉裕康、宮木智、馬越健次(以上、兵庫県立大(旧姫路工業大))、櫻井吉春、伊藤真義、鈴木昌世、豊川秀訓(以上、JASRI)、廣田和馬(東大、物性研)、村上洋一、有馬孝尚(以上、東北大)、浜田典昭、児玉崇(以上、東京理科大)(敬称略)
また、この研究の遂行・発表には、平成12年度・科学研究費「放射光・中性子・電子線を用いた軌道自由度観測技術の開発」及び財団法人ひょうご科学技術協会からの助成を頂きました。
[1]R.von Helmolt, J.Wecher, B.Holzapfel, L.Schultz and K.Samwer : Phys.Rev.Lett.71(1993)2331-2333 ; S.Jin et al.: Science.264(1994)413 ; A.Urushibara et al. : Phys.Rev.B 51(1995-II)14103 ; Y.Moritomo, A.Asamitsu, H.Kuwahara and Y.Tokura : Nature(London)380(1996)141.[2]C.Zener : Phys.Rev.82(1951)403 ; P.W.Anderson and H.Hasegawa : Phys.Rev.100(1955)675 ; P.G.de Gennes : Phys.Rev.118(1960)141.
[3]Y.Tokura and Y.Tomioka : J.Magn.Magn.Mater.200(1999)1 ; A.J.Millis, P.B.Littlewood and B.I.Shraiman : Phys.Rev.Lett.74(1995)5144 ; T.Mizokawa and A.Fujimori : Phys.Rev.B 56(1997-II)R493 ; H.Koizumi, T.Hotta and Y.Takada : Phys.Rev.Lett.80(1998)4518.
[4]A.Koizumi, S.Miyaki, Y.Kakutani, H.Koizumi, N.Hiraoka, K.Makoshi, N.Sakai, K.Hirota and Y.Murakami : Phys.Rev.Lett.86(2001)5589 ; A.Koizumi, T.Nagao, Y.Kakutani, N.Sakai, K.Hirota and Y.Murakami : Phys.Rev.B 69(2004)060401(R) ; A.Koizumi, T.Nagao, Y.Kakutani, N.Hiraoka, N.Sakai, T.Arima, K.Hirota and Y.Murakami : J.Phys.Chem.Solids 66(2005)2183 ; 小泉昭久・坂井信彦,「固体物理」<放射光X線による構造物性研究の最前線>特集号, 37(2002)685.
[5]A.Koizumi, T.Nagao, N.Sakai, K.Hirota and Y.Murakami : to be published in Phys.Rev.B.
[6]M.J.Cooper et al. : X-RAY COMPTON SCATTERING.Oxford University Press Inc., New York(2004).
[7]Y.Tanaka, N.Sakai, Y.Kubo and H.Kawata : Phys.Rev.Lett.70(1993)1537 ; L.Dobrzynski and E.Zukowski : J.Phys.: Condens.Matter 11(1999)8049.
[8]Y.Tanaka et al. : J.Phys.Chem.Solids 61(2000)365 ; Y.Tanaka et al. : Phys.Rev.B 63(2001)045120.
[9]S.Yunoki, T.Hotta and E.Dagotto : Phys.Rev.Lett.84(2000)3714.
[10]S.Okamoto, S.Ishihara and S.Maekawa : Phys.Rev.B 63(2001)104401.
[11]A.M.Olé and F.L.Feiner : Phys.Rev.B 67(2003)092407.
[12]D.G.Lock, V.H.C.Crisp and R.N.West : J.Phys.F: Met.Phys.3(1973)561.
[13]S.Shimomura, N.Wakabayashi, H.Kuwahara and Y.Tokura : Phys.Rev.Lett.83(1999)4389 ; L.Vasiliu-Doloc et al. : Phys.Rev.Let.83(1999)4393 ; M.Kubota et al. : J.Phys, Soc.Jpn.68(1999)2202 ; B.J.Campbell et al. : Phys.Rev.B 67(2003)020409(R).
[14]T.V.Ramakrishnan, H.R.Krishnamurthy, S.R.Hassan and G.Venketeswara Pai : Phys.Rev.Lett.92(2004)157203.
兵庫県立大学大学院 物質理学研究科
〒678-1297 兵庫県赤穂郡上郡町光都3-2-1
TEL:0791-58-0529 FAX:0791-58-0146
e-mail:akihisa@sci.u-hyogo.ac.jp