Volume 17, No.3 Pages 216 - 221

1．はじめに
　凝集系にはミクロからマクロな空間スケールにわたる階層構造を有するものが存在し、それがマクロな機能に重要な役割をする場合がある。例えば細胞を隔てる細胞膜はnmオーダーの特徴的な空間スケールのラメラ（層秩序）構造を有し、細胞内外への物質移動のコントロールや化学反応の場などとして重要な役割を果たす。膜の機能や特徴は膜を構成する分子に大きく依存するが、その詳細はいまだ良く分っていないため、細胞膜の静的・動的な情報を微視的に知ることは生体系の詳細な理解に非常に重要である。生体組織や、その理解の基礎となる基本的な物質についてこれまで階層的な構造、すなわちミクロからマクロなスケールにおける構造については回折などの方法により非常に多くの研究がなされてきた。一方、系の中で物質がどのように運動しているかについても多くの研究がなされてきており、誘電緩和法や赤外分光、ラマン分光、核磁気共鳴法など、非常に多くの測定法が用いられている。これらの方法では、得られた運動の時間スケールと階層的な構造の対応関係を得ることは難しい。しかしながら、各空間スケールで構造がそれぞれどのように運動しているかを知ることは、その系の詳細な理解のために重要である。物理化学的な観点から興味のある系の例として、o-terphenylなどの過冷却液体は、冷却するにつれ内部で分子が共同的に運動するようになると共に局所的なslowβ過程と呼ばれる液体に見られない緩和過程が出現する。両者間の関係はまだ完全には分かっていないが、このような複数の空間スケールの緩和過程が系に混在している場合には、一般に構造の空間スケールごとの緩和を独立に調べることができる準弾性散乱法がその詳細なダイナミクスの理解に有効である。この方法では、エネルギー幅の狭い光や中性子などを、拡散などのダイナミクスを調べたい試料に照射し散乱成分を検出する。このとき、試料中の拡散の度合いに応じてドップラーシフトにより散乱粒子のエネルギーの幅が広がることを利用して、試料のダイナミクスを調べる。さらに、プローブ光（粒子）のエネルギーや散乱角などを選択することで試料との運動量移行qを変化させ、相関を調べたい空間スケールを選択できるという特徴がある。これにより、たとえば複雑な構造を持つ物質においても、その内部で異なるサイズの構造の運動を独立に知ることができる。凝縮系において重要となる運動の時間スケールは10^-15〜1 s（場合によってはさらに長い時間スケール）と非常に幅が広いため、現状では１つの方法ではすべての時間・空間スケールをカバーすることができない。本稿では、核共鳴散乱の⊿E /E〜10^-13という超高分解能を生かして、ほかの方法では十分に測定することのできない原子分子スケールの比較的遅い運動を測定することができる準弾性散乱法である“時間領域干渉計法”と、それを用いて得られた液晶の研究結果について紹介する。

2．時間領域干渉計法
　本研究でターゲットとする緩和現象の空間スケールとしては0.1 nm〜6 nm程度であり、その拡散によるエネルギー幅の広がりはneV程度である。0.1 nm程度の構造を調べるためにX線は大変適したプローブとなるものの、このような微細なエネルギー変化を捉えることは容易なことではない。ところが、⁵⁷Feのように原子核の中には10 keV（波長に換算して〜0.1 nm）オーダーの励起エネルギー（⁵⁷Fe：14.4 keV）を持ちながら、その線幅がneV程度（⁵⁷Fe：4.7 neV）のものが存在する。このような超高分解能のX線（⊿E /E〜10^-13）をプローブ光として準弾性散乱実験に利用することによって、微視的な構造スケールに対応したエネルギー移行の小さな（ゆっくりとした）運動を観測することが出来る。
　このような測定は、放射光が出現する以前には放射性同位体（RI）線源からのγ線を用いて実施されていた^［1］［1］D. C. Champeney: Rep. Prog. Phys. 42 (1979) 1017-1054, and references therein.。しかしながら、RI線源からのγ線には指向性がないこともあって、充分な強度の散乱γ線を得ることは難しく、効率的な実験を行うことは困難であった。それに対して、指向性に優れた放射光を用いることによって、効率的な研究が可能となってきた。その１つの方法は超単色X線を核Bragg散乱によって生成し^{［2, 3］}［2］G. V. Smirnov, V. V. Sklyarevskii, R. A. Voskanyan and A. N. Artem’ev: Pis’ma Zh. Eksp. Teor. Fiz. 9 (1969) 123-127.
［3］G. V. Smirnov, U. van Bürck, A. I. Chumakov, A. Q. R. Baron and R. Rüffer: Phys. Rev. B 55 (1997) 5811-5815.、これを用いてエネルギー領域で測定を行う方法である^［4］［4］R. Masuda, T. Mitsui, Y. Kobayashi, S. Higashitaniguchi and M. Seto: Jpn. J. Appl. Phys. 48 (2009) 120221 (4 pages).。この方法の測定概念を図1に示す。これに対して、本研究で用いた方法は時間領域で干渉現象を利用して準弾性散乱広がりを観測するものである^［5］［5］A. Q. Baron, H. Franz, A. Meyer, R. Rüffer, A. I. Chumakov et al.: Phys. Rev. Lett. 79 (1997) 2823-2826.。この方法では前者の方法に比べ比較的遅い時間スケールにアクセスしやすいという特徴がある。


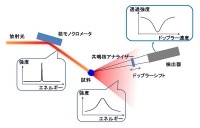
図1　エネルギー領域準弾性散乱法測定概念図。超単色X線を放射光から核モノクロメータ（⁵⁷FeBO₃）による核Bragg散乱により生成し、これを試料に照射する。試料内でneV程度のエネルギー幅の広がりをもたらすような分子（イオン）の運動を観測するためには、同種の原子核（⁵⁷Fe）をドップラーシフトさせることによってエネルギー走査を行う。このアナライザー原子核の幅も核モノクロメータと同様に大変狭いため、アナライザーの後方に検出器を配置することでエネルギー広がりを反映した吸収スペクトルを得ることが出来る。


　ここでは本研究で用いた⁵⁷Feの第一核励起状態からの核共鳴散乱線を用いた時間領域干渉計について考える。図2の時間領域干渉計の概念図に示すように、測定試料に対して放射光入射方向の上流および下流側に同種の共鳴核を含む共鳴核プローブ透過体（以下、透過体）および共鳴核参照体（以下、参照体）を配置する。ここで、後述する理由により透過体と参照体の共鳴エネルギーをドップラー効果により若干異なったものとするため、透過体を動かす事が出来るようになっている。参照体は測定したいスケールに対応した角度に配置する。本研究では、透過体および参照体には、⁵⁷Fe同位体を含みシングルラインの吸収スペクトルを示すことが確認されているフェロシアン化カリウム（K₂Mg⁵⁷Fe(CN)₆）を用いた。このとき、透過体を10 mm/s程度の（往復）等速運動をさせることで励起エネルギーのシフトを起こし、散乱体に比べてμeV程度異なる条件にしておく。また、時間領域で測定を行うためにパルス放射光を使用するが、放射光のエネルギー幅はエネルギー差であるμeVよりも充分に広ければ問題ない。ただ広すぎると、不必要な成分の放射光による測定ターゲットとなるソフトマター試料へのダメージや、時間分解検出器の飽和などの問題を起こすため、実際問題として充分な強度を保つことの可能なmeV程度に分光をしており、今回の場合には核励起エネルギー近傍で3.5 meVに分光した。このようなパルス放射光を、透過体を透過させてから試料に照射する。このときプローブ光として透過体から励起状態の線幅に相当する狭いエネルギー幅の核共鳴前方散乱が、励起状態の寿命（⁵⁷Fe：141 ns）で減衰する指数関数型の時間依存性を示しながら、放射光パルスから遅れて試料に照射される。散乱光を検出する散乱角はBraggの回折条件により、緩和を測定したい空間相関の長さを決定する。ここで、着目する空間相関が100 ns程度の時間スケールで緩和するような状況を想定すると、準弾性散乱広がりは分解能と同程度のneVのオーダーになり、上流の透過体から放射されたプローブ光の線幅にはこの広がりが畳み込まれる。一方、入射放射光それ自体も試料によって散乱され参照体に照射される。この散乱放射光のエネルギー拡がりも生じているはずであるが、充分に幅の広い放射光を用いている場合には、その拡がりによる影響は無視する事が出来る。よって、参照体からも核共鳴前方散乱が放射されるが、線幅の拡がりを受けないため参照光として自然幅のまま検出器に到達する。


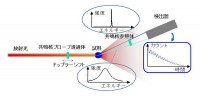
図2　時間領域干渉計の測定概念図。放射光を、ドップラー効果によって励起エネルギーをシフトさせた共鳴核プローブ透過体を透過させてから試料に照射する。共鳴核参照体を測定したいスケールに対応した角度に配置し、試料の散乱光を透過させ、後置の検出器で時間分解測定を行う。


　これらの過程による散乱の干渉効果が時間領域でどのように観測されるかを考えてみる。最初に、試料内の分子による運動が全くない場合を考えてみると、透過体と参照体からの核共鳴散乱は、励起エネルギーを相対的にシフトさせていることに対応して、その時間スペクトル上には、（現在の条件では10 ns程度の）周期のうなり（量子ビート）が指数減衰型のスペクトル上に観測される。これは、異なった固有振動数の２つの音叉をならしたときにうなりが聞こえることを考えると分かりやすいかもしれない。次に、試料内に分子運動が存在する場合には、参照体は自然幅のままであるのに対して透過体からのプローブ光は準弾性散乱過程により広がるので、運動が無かった場合の量子ビートがなまって（減衰して）観測されることになる。その直感的な理由は、線幅が広がるとその分時間領域上のビートの周波数の幅が広がり互いに明瞭性を打ち消し合うように足しあわされる効果のためである。ここで、ビートの減衰する時間定数は、試料の緩和の時間スケールとなる。ゆえにこの緩和を調べることで微視的なダイナミクスの測定が可能になり、現在まで空間スケール0.1〜6 nmの電荷密度の時間スケール1 ns〜10 μsの緩和現象を測定することに成功している。図3に時間領域干渉計法の実験装置の写真を示す。


図3　核共鳴散乱を用いた時間領域干渉計法の実験装置の写真。実線は入射X線を表し、破線は試料により散乱されたX線を表している。電圧−速度トランスデューサーはK₂Mg⁵⁷Fe(CN)₆を定速運動させるために用いている。また、検出器はアバランシェ・フォトダイオード（APD）検出器を用いた。２つのAPD検出器はそれぞれ低角と高角での準弾性散乱を検出するために用いられている。また、試料には、実験条件に応じて温度変化や磁場印加が可能となっている。


　なお、核共鳴励起過程を用いた分光法としては、メスバウアー分光法や核共鳴非弾性散乱法など存在するが、これらと違い、本測定においては共鳴同位体を試料中に含む必要はない。これは本方法が原子核の励起状態の狭い線幅を用いているだけで、特に共鳴励起過程そのものを用いて試料の性質を調べている訳ではないからである。

3．時間領域干渉計による液晶の運動性の研究
　時間領域干渉計法によるソフトマターのスローダイナミクス研究として、２種の液晶のダイナミクス測定を行った^［6］［6］M. Saito, M. Seto, S. Kitao, Y. Kobayashi, M. Kurokuzu et al.: J. Phys. Soc. Jpn. 81 (2012) 023001 (4 pages).。実験はSPring-8、BL09XUにて行われた。測定に用いた試料は、炭化水素鎖を有する典型的液晶分子の4-cyano-4'-octylbiphenyl(8CB) および液晶分子の炭化水素鎖の一部の水素をフッ素置換した両親媒性液晶分子11-(4'-cyanobiphenyl-4-yloxy)undecyl pentadecafluorooctanoate(BI) である。両者の分子構造をそれぞれ図4（A）および（B）に示す。スメクティック相中では図4（C）に示されているように液晶分子の重心位置が層秩序構造を有し、分子を棒と考えたときその棒の向きは層内で比較的そろっておりかつ分子は運動性を有する状態となっている。ここで、8CBの場合、炭化水素鎖とベンゼン環の部分は混ざり合いやすいため、分子はどちらの向きでも層構造を形成できる。一方、BI分子を構成するフッ素鎖と、炭化水素から構成される部分は互いに混ざり合いにくいことが知られているため、BI分子はスメクティック相において層構造中でフッ素鎖と炭化水素から構成される部分が互いにミクロに分離した、生体膜などのリオトロピック液晶で見られるようなラメラ構造をとる可能性が示唆されている。

　 　 　
図4 （A）8CB、および（B）BIの分子構造と静的構造因子S(q) 、および検出器の配置qの関係。（C）はスメクティック相での分子配置の概念図。（A）、（B）でそれぞれ低角、高角側のピークは（C）での層間、層内の分子間相関を反映している。


　まず、スメクティック相状態にある液晶8CBに磁場を印加することで分子の配向を揃え、図4（A）で示すS(q) の２つのピーク（低角：層内の相関、高角：層間の相関を反映）に対応するqに検出器を置くことで、分子運動の異方性の測定を行った。8CBとBIでそれぞれ４、11時間程度の測定の結果得られた核共鳴散乱Ｘ線の時間スペクトルを図5（A）、（B）に示す。ビートの緩和を指数関数モデルで解析することにより、層間および層内の分子間相関の緩和時間として、それぞれ298(49)nsおよび18(7)nsという値が得られ（括弧内の数字は得られた緩和時間の測定誤差）、異方的な空間相関の緩和時間を得ることができた。また、この測定時間は誘電緩和法で得られた異方的な緩和の時間スケールと整合することを確認した。一方、BI分子を構成するフッ素鎖と炭化水素鎖は互いに混ざり合いにくいことが知られているが、もしそのようなミクロな分離が起きていれば、層間の緩和時間は層内の緩和時間に比べて数倍程度大きくなることが示唆されている。これを調べるため、時間領域干渉計法を用いてスメクティック相状態にあるBIに対して同様の測定を行い図5（B）で示す時間スペクトルを得た。そして、解析により層間および層内の分子間相関の緩和時間としてそれぞれ225(47)nsおよび33(17)nsという値を得ることができ、その緩和の時間スケールはそれぞれ8CBとほぼ同程度であることを確認した。この結果はBIのスメクティック相状態ではフッ素鎖と炭化水素鎖が大きく分離していないことを示唆しており、これより分子運動性の観点から液晶の内部の構造に関する知見を得ることができた。この系に全フッ素置換された炭化水素を加えることでミクロな非相溶性が顕著になることが考えられるため、今後ミクロにフッ素鎖と炭化水素鎖が分離した状態の運動性を調べ、ミクロな構造を運動性の観点からさらに研究し、追及して行きたいと考えている。

　 　
図5 （A）8CB、および（B）BIに対してそれぞれ得られた時間スペクトル。低角、高角の検出器で得られたスペクトルはそれぞれスメクティック層間、層内の分子間相関の緩和が反映されている。どちらの液晶でも層間に比べ層内の分子間相関の方が早く緩和するため、それを反映して高角で得られたスペクトルにおけるビートが不明瞭になっている。

4．今後の展望
　これまでの時間領域干渉計の実験結果から、0.1〜6 nmの空間スケールにおいて複数の空間スケールの空間相関が存在する系においても、散乱角を選択することで調べたい空間スケールを決めてその運動性を知ることができた。この特徴はさらに複雑な物質中でも、個々の内部構造の運動性を独立に知ることを可能とする。今後の測定効率の改善策として、プローブとしての核共鳴散乱X線を放射する核共鳴吸収体を追加した測定系や、エネルギー分解能はそのままで、複数のエネルギーで核励起を起こす核共鳴吸収体を用いて時間領域干渉計を構築することで、今後１桁程度測定時間が短縮可能なことが示唆されている^［7］［7］M. Saito, M. Seto, S. Kitao, Y. Kobayashi, M. Kurokuzu et al.: Hyperfine Interact. 206 (2012) 87-90.。また、現在測定がなされた時間スケールは数ns〜10 μsであるが、時間領域干渉計に用いる核種の選択性^［8］［8］M. Saito, M. Seto, S. Kitao, Y. Kobayashi, S. Higashitaniguchi et al.: Appl. Phys. Express 2 (2009) 026502 (4 pages).、各時間スケールに最適な実験条件等を明らかにすることで、さらに広い範囲をカバーできる可能性がある。0.1〜6 nmは、原子分子の空間スケールであり、本質的に多くの応用対象が存在すると考えられる。今後さらに過冷却液体や生体膜のモデル系などのソフトマターの微視的なスローダイナミクスを調べることで、その物理現象や生体系への寄与を明らかにしたいと考えている。

5．謝辞
　本研究は、京都大学大学院理学研究科の山本潤教授、高輝度光科学研究センターの依田芳卓博士、京都大学原子炉実験所の北尾真司准教授、小林康浩助教、黒葛真行氏との共同研究で行われた。本研究にあたり、高エネルギー加速器研究機構の岸本俊二博士には検出器の開発にご協力いただいた。また、大日本インキ化学工業株式会社の西山伊佐博士には試料BIを提供していただくとともに、京都大学大学院理学研究科の高西陽一准教授には有益なアドバイスをいただいた。実験はSPring-8のBL09XUで行われた（課題番号2011A0086）。また本研究JST戦略的創造研究推進事業 チーム型研究（CREST）「物質現象の解明と応用に資する新しい計測・分析基盤技術」研究領域（研究総括：田中通義 東北大学 名誉教授）の研究課題「物質科学のための放射光核共鳴散乱法の研究」（研究代表者：瀬戸 誠）、特別研究員奨励費（225287）の助成を受けて行われた。

参考文献
［1］D. C. Champeney: Rep. Prog. Phys. 42 (1979) 1017-1054, and references therein.
［2］G. V. Smirnov, V. V. Sklyarevskii, R. A. Voskanyan and A. N. Artem’ev: Pis’ma Zh. Eksp. Teor. Fiz. 9 (1969) 123-127.
［3］G. V. Smirnov, U. van Bürck, A. I. Chumakov, A. Q. R. Baron and R. Rüffer: Phys. Rev. B 55 (1997) 5811-5815.
［4］R. Masuda, T. Mitsui, Y. Kobayashi, S. Higashitaniguchi and M. Seto: Jpn. J. Appl. Phys. 48 (2009) 120221 (4 pages).
［5］A. Q. Baron, H. Franz, A. Meyer, R. Rüffer, A. I. Chumakov et al.: Phys. Rev. Lett. 79 (1997) 2823-2826.
［6］M. Saito, M. Seto, S. Kitao, Y. Kobayashi, M. Kurokuzu et al.: J. Phys. Soc. Jpn. 81 (2012) 023001 (4 pages).
［7］M. Saito, M. Seto, S. Kitao, Y. Kobayashi, M. Kurokuzu et al.: Hyperfine Interact. 206 (2012) 87-90.
［8］M. Saito, M. Seto, S. Kitao, Y. Kobayashi, S. Higashitaniguchi et al.: Appl. Phys. Express 2 (2009) 026502 (4 pages).

齋藤　真器名　SAITO Makina
Sincrotrone Trieste
Beamlines Spectroscopy/Scattering
〒34149 Strada Statale 14 - km 163,5 in AREA Science Park, Basovizza, Trieste ITALY
TEL：+39 040 37581
e-mail：makina.saito@elettra.trieste.it

瀬戸　誠　SETO Makoto
京都大学　原子炉実験所
〒590-0494　大阪府泉南郡熊取町朝代西二丁目1010-1
TEL：072-451-2445
e-mail：seto@rri.kyoto-u.ac.jp
日本原子力研究開発機構　量子ビーム応用研究部門
〒679-5148　兵庫県佐用郡佐用町光都1-1-1