Volume 26, No.4 Pages 349 - 355

1. はじめに
　デバイスや材料の微細構造化・複合化が進み、その構造−機能相関の理解と特性制御には、ナノメートルからマイクロメートルに亘る空間階層構造を機能中の動態や劣化過程も含めて可視化することが重要となっている。我々は、動作中のデバイスや機能環境中の材料試料の非侵襲構造評価に向けて、硬X線コヒーレント回折イメージング（coherent diffraction imaging, CDI）法の開発に取り組んできた^[1-3][1] Y. Takayama, Y. Takami, K. Fukuda, T. Miyagawa and Y. Kagoshima: J. Synchrotron Rad. 25 (2018) 1229-1237.
[2] Y. Takayama, Y. Tsusaka, Y. Kagoshima, S. Kuwamoto, Y. Urushihara et al.: SPring-8/SACLA annual report FY2018 (2020) 132-135.
[3] Y. Takayama, K. Fukuda, M. Kawashima, Y. Aoi, D. Shigematsu et al.: Commun. Phys. 4 (2021) 48.。
　CDIはレンズレスイメージング法の1種であり、硬X線領域では加工の難しい対物レンズの代わりに計算機アルゴリズムを像形成に用いることで、高い空間分解能を実現する^[4,5][4] J. Miao, P. Charalambous, J. Kirz and D. Sayre: Nature 400 (1999) 342-344.
[5] H. M. L. Faulkner and J. M. Rodenburg: Phys. Rev. Lett. 93 (2004) 023903.（図1）。具体的には、アンジュレータから放射される空間的にコヒーレントなX線で試料を照明し、試料遠方でフラウンホーファー回折パターンを計測する。その回折強度分布は試料透過波動場のフーリエ振幅の二乗に比例するため、反復的位相回復アルゴリズム^[6-8][6] J. R. Fienup: Appl. Opt. 21 (1982) 2758-2769.
[7] A. M. Maiden and J. M. Rodenburg: Ultramicroscopy 109 (2009) 1256-1262.
[8] P. Thibault, M. Dierolf, A. Menzel, O. Bunk, C. David et al.: Science 321 (2008) 379-382.により失われた位相情報を復元することで、逆フーリエ変換により試料電子密度に比例する位相コントラストと化学状態を反映した吸収コントラストの投影像を同時に再生することができる。短波長かつ透過能の高い硬X線をプローブとし、計算機トモグラフィ（computed tomography, CT）と組み合わせることで、電子線が透過しないマイクロメートル以上の厚みの試料の三次元構造を非侵襲で内部まで観察可能である。

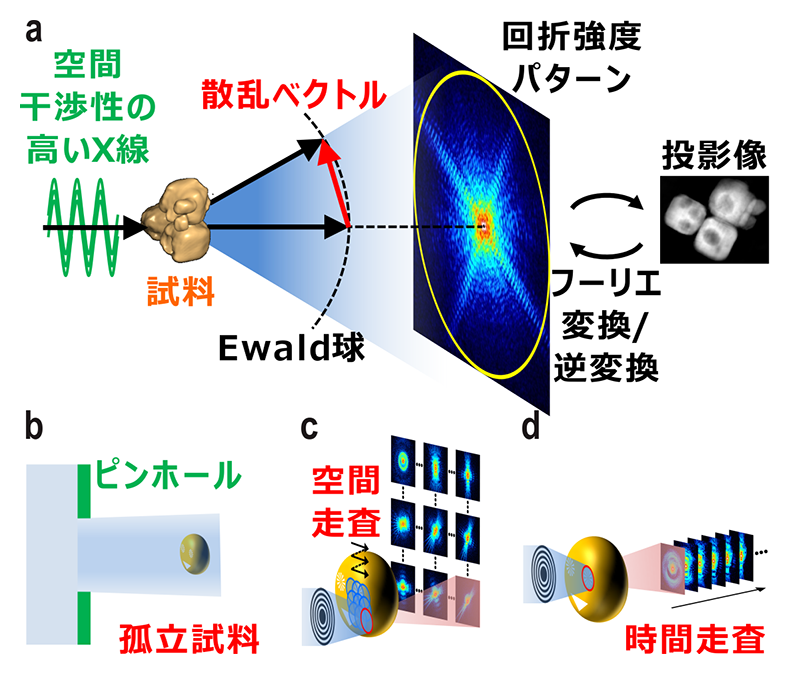
図1　(a) CDI法の原理、(b) 平面波照明CDI、(c) タイコグラフィ、(d) マルチショットCDIの模式図。

　J. Miaoによる1999年の実証実験^[4][4] J. Miao, P. Charalambous, J. Kirz and D. Sayre: Nature 400 (1999) 342-344.以降、CDIは世界中の放射光施設で開発が急速に進められてきた。初期のCDI（図1b）は試料全体を平面波中に浴し、試料形状を拘束条件として位相回復を行うため^[6][6] J. R. Fienup: Appl. Opt. 21 (1982) 2758-2769.、対象はマイクロメートルサイズ以下の粒子状試料に限られていた。一方、局所照明による走査型CDIであるタイコグラフィ（ptychography; 図1c）^[5][5] H. M. L. Faulkner and J. M. Rodenburg: Phys. Rev. Lett. 93 (2004) 023903.が2004年に提案された。照射野の一部が重なるように計測し、重畳領域の構造が一致するよう位相回復することで非粒子状試料の局所イメージングが可能となり^[7,8][7] A. M. Maiden and J. M. Rodenburg: Ultramicroscopy 109 (2009) 1256-1262.
[8] P. Thibault, M. Dierolf, A. Menzel, O. Bunk, C. David et al.: Science 321 (2008) 379-382.、その応用の幅は格段に広がった。
　本稿では、我々が兵庫県IDビームラインBL24XUに構築した各種CDIシステムについて紹介する。我々は、特にデバイス動作や複合材料の各種応答における構造動態のオペランド／その場観察を目指して、大気環境下で計測可能な平面波照明CDI及びタイコグラフィ装置を開発し^[1,2][1] Y. Takayama, Y. Takami, K. Fukuda, T. Miyagawa and Y. Kagoshima: J. Synchrotron Rad. 25 (2018) 1229-1237.
[2] Y. Takayama, Y. Tsusaka, Y. Kagoshima, S. Kuwamoto, Y. Urushihara et al.: SPring-8/SACLA annual report FY2018 (2020) 132-135.、2019年から供用して産業利用を中心に応用展開を図ってきた。更に、未開発であったCDIによる動的イメージング法を、新たな着想の位相回復アルゴリズムと照明光学系を組み合わせたマルチショットCDI法（図1d）の開発により実現し、従来より100倍以上高い10−100ミリ秒時間分解能での動的試料の動画観察に成功した^[3][3] Y. Takayama, K. Fukuda, M. Kawashima, Y. Aoi, D. Shigematsu et al.: Commun. Phys. 4 (2021) 48.。

2. 平面波照明CDI・タイコグラフィ
　我々は、まず機能性粒子のナノ構造動態のその場観察に向けて、大気環境下やガス雰囲気下での計測が可能な平面波照明CDIシステムを構築し^[1][1] Y. Takayama, Y. Takami, K. Fukuda, T. Miyagawa and Y. Kagoshima: J. Synchrotron Rad. 25 (2018) 1229-1237.、続いてデバイスのオペランド観察や複合材料の各種応答のその場観察を目指して、タイコグラフィによる非粒子状試料の局所観察へと高度化した^[2][2] Y. Takayama, Y. Tsusaka, Y. Kagoshima, S. Kuwamoto, Y. Urushihara et al.: SPring-8/SACLA annual report FY2018 (2020) 132-135.（図2a）。照明光学系には、平面波照明CDIではピンホール光学系、タイコグラフィでは次項で詳述するゾーンプレート縮小投影照明光学系を採用しており、光子エネルギー7−10 keVで運用している。計測ソフトウェアは二次元イメージングの他、CTやエネルギー走査測定が可能であり、位相回復計算による投影像の再生までを自動で実行する。これまでに二次元で～10 nm、三次元で～40 nmの空間分解能を達成している（図2b-d）。応用先はエネルギー・電子デバイス材料や有機材料、構造材料など多岐に亘る。

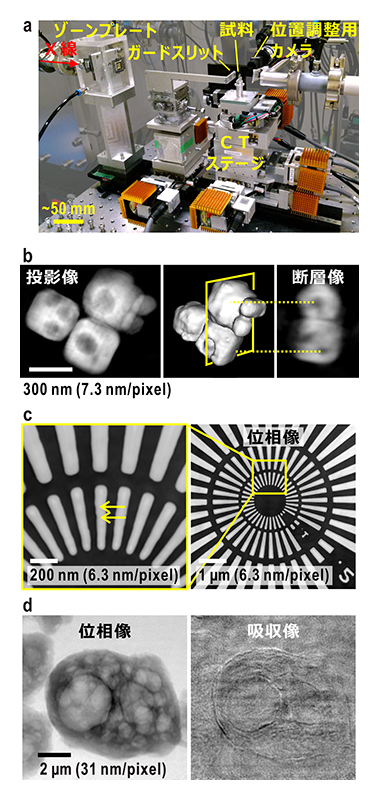
図2　(a) 大気環境型タイコグラフィ装置。1.4～3.1 m上流のピンホール像をゾーンプレートで試料上に縮小結像して照明し、4.5～3.3 m下流の二次元検出器で回折パターンを計測する。(b) 平面波照明CDI-CTによる金コロイド粒子内部空隙の可視化。(c, d) タイコグラフィによるタンタル製分解能チャートでの空間分解能評価(c)及び、複合樹脂材料（位相物体）の可視化(d)。

　平面波照明CDIは完浴型であるため試料ドリフトに鈍感かつ時間分解能が高い利点があり、2 μm程度以下の粒子を対象に多孔質粒子の湿潤空気雰囲気下での毛管凝縮^[1][1] Y. Takayama, Y. Takami, K. Fukuda, T. Miyagawa and Y. Kagoshima: J. Synchrotron Rad. 25 (2018) 1229-1237.や構造化燃料電池触媒の酸化還元ガス雰囲気下での初期エージング^[9][9] 伊藤孝憲、今井英人、黒木秀紀、田巻孝敬、山口猛央他：第16回SPring-8産業利用報告会予稿集 (2019) P044/H-13.のその場観察を実現した。タイコグラフィでは、広視野投影イメージングやFIB加工により5−10 μm角のピラー状に切り出した試料の位相CT観察が実施されており、自動車塗膜のバインダー樹脂中TiO₂顔料粒子^[10][10] 末広省吾、幸坂崇、小林秀雄、高山裕貴：塗装工学 56 (2021) 204-210.やゴム中フィラー粒子の分散状態、エンジン内堆積物の加熱硬化形成過程に起因した不均一な組成分布^[11][11] 末広省吾、辻下昌之、相良啓太、幸坂崇、高山裕貴：第18回SPring-8産業利用報告会予稿集 (2021) P25/HO-01.、構造材料の力学特性と相関したメソ構造などを可視化した。タイコグラフィの位相コントラストは定量性が高く、～0.1 g/cm³程度の密度差に相当するコントラストが得られている。他に、吸収端を利用した化学状態の可視化やMEMS（Micro Electro Mechanical Systems）ヒーターによる加熱環境下での観察も進めている。

3. マルチショットCDIの開発
　開発したCDIシステムを更にオペランド／その場動的イメージングへ展開する上で、既存のCDI技術には大きな課題があった。計測上、（1）局所イメージングが可能なタイコグラフィは走査型であるため、照射野の移動に0.1−0.3秒程度のオーバーヘッドが生じ、数秒～数十秒より高い時間分解能の実現は困難であった。また、位相回復アルゴリズムでは、（2）動的な試料は回折パターン1フレームの露光中も構造が時々刻々と変化するが、これまで提案されたアルゴリズムは静的な回折データを仮定していること、（3）動的イメージング向けとして提案されたアルゴリズム^[12,13][12] Y. H. Lo, L. Zhao, M. Gallagher-Jones, A. Rana, J. J. Lodico et al.: Nat. Commun. 9 (2018) 1826.
[13] G. N. Hinsley, C. M. Kewish and G. A. van Riessen: Opt. Exp. 28 (2020) 36862-36872.も拘束条件として視野内の一部が静的であることを前提としており、対象が限定的であることが課題であった。そのため、視野内全体で構造変化が生じる系でのCDIによる動的イメージングは実現しておらず、秒より速い時間スケールのナノダイナミクスは時分割小角散乱やX線光子相関分光法などにより逆空間で計測されてきた。
　そこで我々は、動的試料の特徴を位相回復アルゴリズムに取り入れることで上記課題を解決した、マルチショットCDI法（図1d）を開発した^[3][3] Y. Takayama, K. Fukuda, M. Kawashima, Y. Aoi, D. Shigematsu et al.: Commun. Phys. 4 (2021) 48.。本手法では、試料上のイメージング領域を局所照明し、時間走査により時分割回折データセットを取得して、全時間フレームに亘って位相回復アルゴリズムを適用する。タイコグラフィのように空間走査を行わないため、検出器フレームレート程度の時間分解能が期待できる。例えば、光子計数型検出器EIGER X 1M（Dectris Ltd, Switzerland）では最大3,000 fpsである。また、測定系はタイコグラフィと共通であり、タイコグラフィによる広視野イメージングとマルチショットCDIによる局所動的イメージングを相補的に用いることができる。
　時分割回折データセットからの位相回復を実現するために、我々はタイコグラフィで用いられるextended Ptychographic Iterative Engine（ePIE）^[7][7] A. M. Maiden and J. M. Rodenburg: Ultramicroscopy 109 (2009) 1256-1262.を基に、マルチフレーム位相回復法^[3][3] Y. Takayama, K. Fukuda, M. Kawashima, Y. Aoi, D. Shigematsu et al.: Commun. Phys. 4 (2021) 48.を開発した（図3）。本手法では、1フレーム露光中の試料構造変化を扱うために、試料像をサブフレーム分割し、各サブフレームから計算される回折強度の和として計測データを表現する。即ち、n番目の回折強度フレームI_nを2L + 1枚のサブフレームI_n,lに分割し、

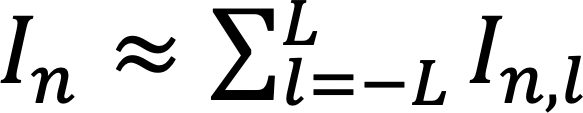･･･ (1)

と表す。ここで、I_n,lは、対応する試料複素透過率像サブフレームO_m+lと時間に依存しない照射波動場Pを用いて、

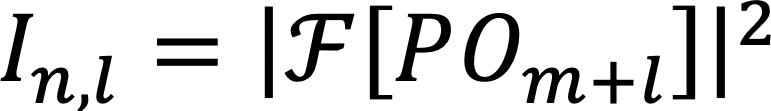･･･ (2)

と表せる。Ψ_m+l ≡ PO_m+lが試料直後の透過波動場であり、フーリエ変換演算子により、検出器面でのフラウンホーファー回折波動場[Ψ_m+l]を得る。本研究ではL = 1として3枚のサブフレームに分割した。照射波動場Pはタイコグラフィにより実験的に計測できるので、回折強度フレームI_nの計測値と計算値の誤差を最小化するように試料サブフレームO_m+lの最適化問題を考えると、次の更新式を得ることができる。

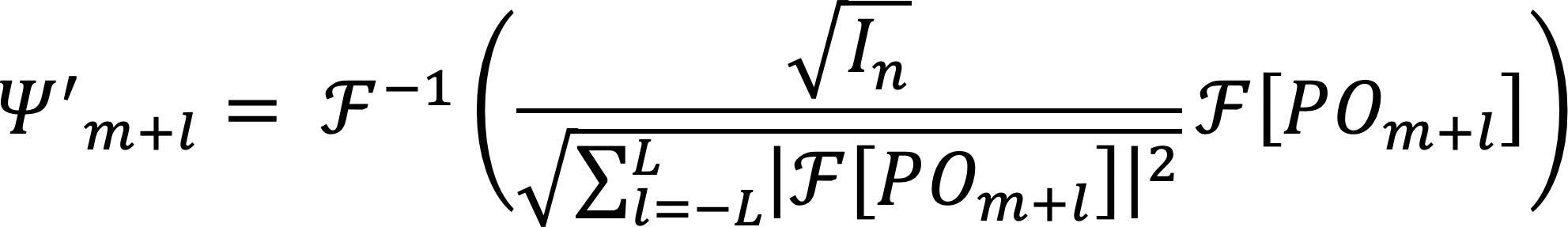	･･･ (3)
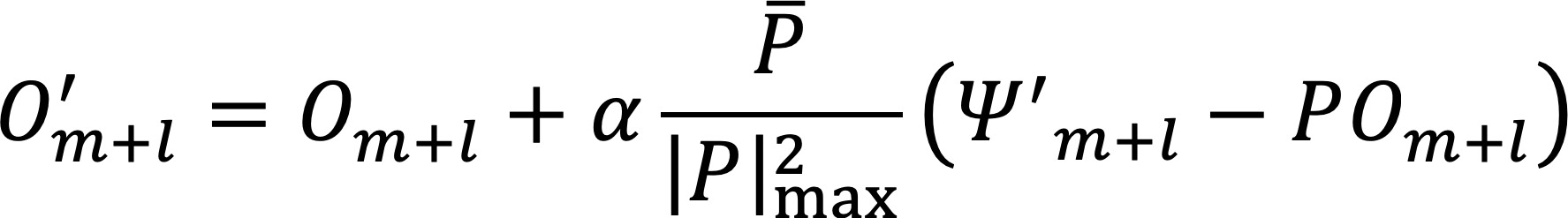	･･･ (4)

　PはPの複素共役である。式(3)にて途中解O_m+lから計算される回折波動場の振幅を、計測値と式(1)-(2)による計算値の比でスケーリングして逆フーリエ変換することで試料透過波動場Ψ_m+lを更新し、式(4)にて更新前後の透過波動場の差分から試料サブフレームO_m+lの変化分を算出して更新前のO_m+lに加える。ここで、更新量はフィードバックパラメーターαで調整され、また照明強度の最大値 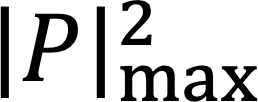でスケーリングすることでノイズの影響を低減する。式(3)-(4)の操作を全ての試料サブフレームに適用して1反復とし、250−400反復して収束解を得る。

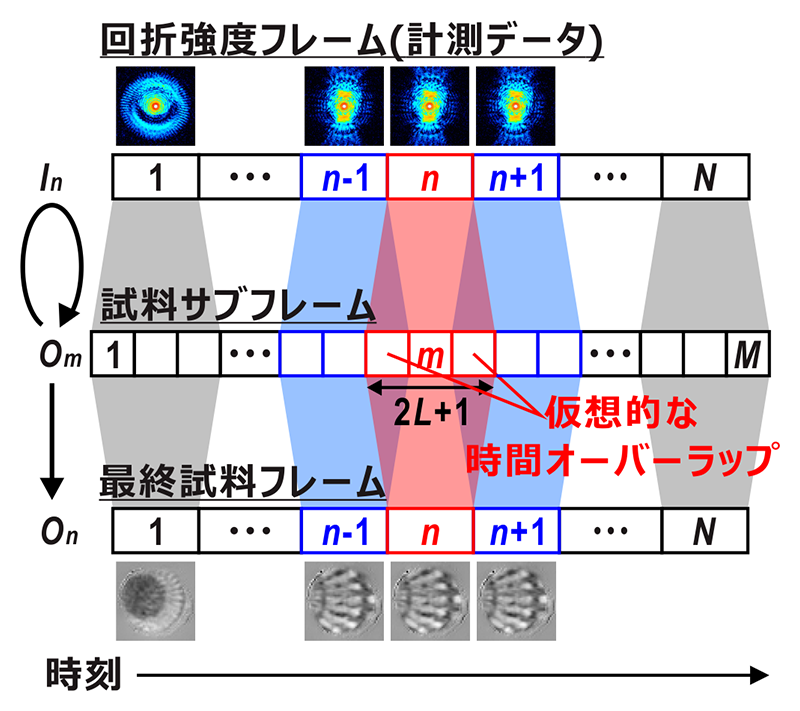
図3　マルチフレーム位相回復法の模式図。

　ただし、上式による更新では各試料サブフレーム間はほとんど相関しておらず、高い収束性を実現できない。そこで、新たな着想として構造変化が時間的及び空間的に連続に生じることに着目し、隣接する試料サブフレームを相関させる2つの拘束条件を導入した。まず、各時間フレームの境界に位置する試料サブフレームは前後の時間フレームで共通とする仮想的な時間オーバーラップを導入し、再生する動的イメージの時間連続性を担保した（図3）。また、圧縮センシングで用いられる全変動正則化^[14,15][14] L. I. Rudin, S. Osher and E. Fatami: Phys. D 60 (1992) 259-268.
[15] A. Chambolle: J. Math. Imag. Vis. 20 (2004) 89-97.を動的イメージの時間及び空間方向に適用することで、時空間方向の連続性の向上を図った。全変動正則化は、動画像の画素値の勾配の絶対値総和が小さくなるよう制約を課すものであり、構造特徴を保存しながら、より時空間連続性の高い解に近付けることができる。試料サブフレームの時刻は不定なため、収束解のサブフレームを時間方向にビニングして元のフレームレートに戻し、最終像とした。
　マルチフレーム位相回復アルゴリズムを適切に機能させるには、照明光学系の開発も必要であった。通常の照明光学系は無限遠にある光源像を試料上に投影するため、回折により裾野が広がる（図4a）。試料の空間走査を行わない場合、照明強度の低い領域は再生像のシグナル対ノイズ比が低下するだけでなく、位相回復計算の更新量も抑えられ、像の更新が視野内で不均一になるため解への収束が難しくなる。そこで我々は、照明強度の均一なトップハットビームを形成するために、縮小投影照明光学系を開発した（図4b）。本光学系では直径～20 μmのピンホールをコヒーレント照明し、そのピンホール像をゾーンプレートで縮小して試料上へ結像する。空間分解能～100 nmのゾーンプレート（FZP-S86/416; NTT-AT, Japan）を用いて縮小倍率1/5−1/10の縮小投影光学系を構築し、図4cのように波動光学シミュレーションを良く再現するトップハットビームを形成することができた。現在、BL24XUのタイコグラフィ及びマルチショットCDIに採用している。

図4　(a) 通常の照明光学系と、(b) 縮小投影照明光学系の波動光学シミュレーション。縮小投影照明光学系では、焦点距離をfとして、ピンホール、ゾーンプレート及び試料が薄レンズの公式1/a + 1/b = 1/fを満たすように配置される。(c) タイコグラフィにより実測した縮小投影照明波動場。振幅を明度、位相を色相で表示している。縮小倍率は1/12(b)と1/5(c)。

4. マルチショットCDIの実証
　まず、金コロイド粒子分散系のブラウン運動シミュレーションによってマルチショットCDIの可視化性能を評価し、続いてタンタル製分解能チャートの並進運動を動的イメージングすることで実証実験を行った^[3][3] Y. Takayama, K. Fukuda, M. Kawashima, Y. Aoi, D. Shigematsu et al.: Commun. Phys. 4 (2021) 48.。何れも光子エネルギーを8 keVとし、シミュレーションはBL24XUでの実装を基に波動光学計算で得た照明波動場を用いて行った。
　金コロイド粒子ブラウン運動のマルチショットCDIシミュレーション結果の一部を図5に示す。金コロイド粒子直径は400 nm、分散媒をグリセリン水溶液とし、グリセリン濃度及び系の温度を変えることでブラウン運動の根平均二乗変位（root mean square displacement, RMSD）を0.16−3.22 pixels/frame（40 nm/pixel）の範囲で調整し、10 ms/frameでマルチショットCDIシミュレーションを行った。RMSD 0.64 pixels/frameでも回折パターンの干渉縞（スペックルと呼ばれる）は鮮明であり、個々のフレームはほぼ静的であるとみなせる。一方、RMSD 3.22 pixels/frameでは、スペックルは1フレーム露光中に時間平均されて不鮮明である。それにもかかわらず、マルチフレーム位相回復アルゴリズムにより、何れのブラウン運動もモデルを良く再現する動的イメージを再生することに成功した。ePIEによる再生では位相像でも粒子位置の判別は難しく^[3][3] Y. Takayama, K. Fukuda, M. Kawashima, Y. Aoi, D. Shigematsu et al.: Commun. Phys. 4 (2021) 48.、提案手法による動的イメージング性能の劇的な改善が分かる。また、マルチフレーム位相回復では、硬X線領域では本質的に低コントラストである吸収像も明瞭に可視化された。吸収像が可視化されたことで、吸収端近傍でマルチショットCDIを行うことにより、特定元素の空間分布変化の可視化や、化学状態の変化をコントラストの明滅として捉えることができると期待される。

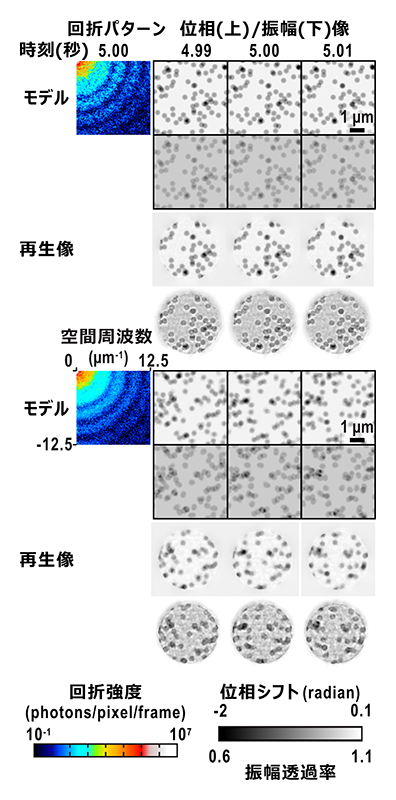
図5　金コロイド粒子ブラウン運動系でのマルチショットCDIシミュレーション。RMSD 0.64（上）及び、3.22（下）pixels/frame。

　続いて、逆空間での計測では解釈が難しい系として、タンタル製分解能チャート（XRESO-50HC; NTT-AT, Japan）を125 nm/sで並進運動させ、その過程をマルチショットCDIにより100 ms/frameで可視化した（図6）。再生した動的イメージの画素サイズは43 nmであり、並進速度は0.29 pixels/frameに相当する。時分割測定により1フレーム当たりの露光量はタイコグラフィと比べて著しく低下するため、タイコグラフィ像（図2c）と比較すると空間分解能は制限されるが、79 nmの線幅まで解像可能な動的イメージを再生することに成功した。開発当時は検出器のダイナミックレンジにより照射フラックスが～3 × 10⁷ photons/sに制限されていたが、現在では特に光子計数率が高い回折パターンの原点付近にシリコン製の減衰板を挿入し、更に部分コヒーレンスを取り扱う混合状態アルゴリズム^[16][16] P. Thibault and A. Menzel: Nature 494 (2013) 68-71.をマルチフレーム位相回復法に組み込むことで、照射可能なフラックスを10倍向上している。また、視野（ビームサイズ）も4 μmに拡大した（図4c）。次世代放射光でのコヒーレントフラックス増大により、更なる時空間分解能の向上と応用機会の拡大が期待される。

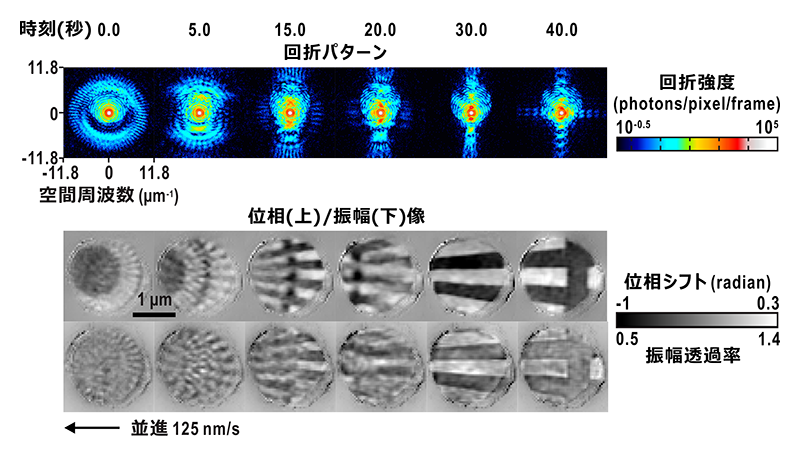
図6　タンタル製分解能チャート並進運動でのマルチショットCDI実証実験。

5. 将来展望
　今後、オペランド／その場観察へと展開する上で、回折限界に起因する試料厚みの制限は避けられない問題である。回折限界空間分解能Δでイメージングする場合、試料は被写界深度（depth of field, DoF）内に浴する必要があり、イメージング波長をλと置くと、DoF～Δ²/λとなる^[17,18][17] Y. Kagoshima and Y. Takayama: J. Synchrotron Rad. 26 (2019) 52-58.
[18] A. Suzuki, S. Furutaku, K. Shimomura, K. Yamauchi, Y. Kohmura et al.: Phys. Rev. Lett. 112 (2014) 053903.。例えば、10 nmの空間分解能を目指すと試料厚み上限はミクロンオーダーとなる。この関係はレンズレス／レンズベースを問わないが、波動伝播過程に基づいて試料像を再生するCDIの場合、試料を伝播方向に分割して試料内波動伝播も含めて取り扱うことで、DoFを超えた厚みの試料の深さ分解イメージングが可能なことがタイコグラフィで示されている^[18,19][18] A. Suzuki, S. Furutaku, K. Shimomura, K. Yamauchi, Y. Kohmura et al.: Phys. Rev. Lett. 112 (2014) 053903.
[19] A. M. Maiden, M. J. Humphery and J. M. Rodenburg: J. Opt. Soc. Am. A 29 (2012) 1606-1614.。マルチショットCDIでもこのアプローチを取ることで、深さ分解・動的イメージングへと展開していきたい。厚い試料を対象とすることで散乱断面積を補うことができ、時空間分解能の向上も期待できる。また、材料特性は多元化や結晶相の制御により向上が図られており、元素や化学状態、結晶相の空間分布を同時に可視化することも重要である。マルチコントラスト化についても、マルチショットCDIを応用した、DoFの回折限界を超える手法の開発に着手したところである。今後も、レンズレスイメージング技術を深化させることで、高度でユニークな可視化研究を実現し、放射光科学と応用諸分野の発展に貢献していきたい。

謝辞
　本研究は、兵庫県立大学大学院理学研究科X線光学分野において、篭島靖教授、髙見侑希氏、福田敬三氏、青井雄幹氏、赤田樹氏、川島基樹氏、重松大樹氏、松崎彬氏、沼田あゆみ氏らと共同で実施された。また、研究遂行及び技術供用化にあたってご支援頂いた兵庫県ビームラインスタッフ各位、実用展開に向けてサンプル提供や有益なフィードバックを頂いているユーザー各位に深く感謝申し上げる。本研究は日本学術振興会科研費 若手研究（16K21621、19K14678）、兵庫県立大学 特別研究助成（2016）、公益財団法人ひょうご科学技術協会 学術研究助成（2017）、株式会社東芝 研究開発センター（2017-2020）などの支援を受けて実施された。本稿で紹介したCDI技術の開発は、SPring-8兵庫県IDビームラインBL24XUにおいて、課題番号2016A3200、2016B3201、2017A3201、2017B3201、2018A3201、2018B3201、2019A3201、2019A3297、2019B3201、2020A3201として実施された。

参考文献
[1] Y. Takayama, Y. Takami, K. Fukuda, T. Miyagawa and Y. Kagoshima: J. Synchrotron Rad. 25 (2018) 1229-1237.
[2] Y. Takayama, Y. Tsusaka, Y. Kagoshima, S. Kuwamoto, Y. Urushihara et al.: SPring-8/SACLA annual report FY2018 (2020) 132-135.
[3] Y. Takayama, K. Fukuda, M. Kawashima, Y. Aoi, D. Shigematsu et al.: Commun. Phys. 4 (2021) 48.
[4] J. Miao, P. Charalambous, J. Kirz and D. Sayre: Nature 400 (1999) 342-344.
[5] H. M. L. Faulkner and J. M. Rodenburg: Phys. Rev. Lett. 93 (2004) 023903.
[6] J. R. Fienup: Appl. Opt. 21 (1982) 2758-2769.
[7] A. M. Maiden and J. M. Rodenburg: Ultramicroscopy 109 (2009) 1256-1262.
[8] P. Thibault, M. Dierolf, A. Menzel, O. Bunk, C. David et al.: Science 321 (2008) 379-382.
[9] 伊藤孝憲、今井英人、黒木秀紀、田巻孝敬、山口猛央他：第16回SPring-8産業利用報告会予稿集 (2019) P044/H-13.
[10] 末広省吾、幸坂崇、小林秀雄、高山裕貴：塗装工学 56 (2021) 204-210.
[11] 末広省吾、辻下昌之、相良啓太、幸坂崇、高山裕貴：第18回SPring-8産業利用報告会予稿集 (2021) P25/HO-01.
[12] Y. H. Lo, L. Zhao, M. Gallagher-Jones, A. Rana, J. J. Lodico et al.: Nat. Commun. 9 (2018) 1826.
[13] G. N. Hinsley, C. M. Kewish and G. A. van Riessen: Opt. Exp. 28 (2020) 36862-36872.
[14] L. I. Rudin, S. Osher and E. Fatami: Phys. D 60 (1992) 259-268.
[15] A. Chambolle: J. Math. Imag. Vis. 20 (2004) 89-97.
[16] P. Thibault and A. Menzel: Nature 494 (2013) 68-71.
[17] Y. Kagoshima and Y. Takayama: J. Synchrotron Rad. 26 (2019) 52-58.
[18] A. Suzuki, S. Furutaku, K. Shimomura, K. Yamauchi, Y. Kohmura et al.: Phys. Rev. Lett. 112 (2014) 053903.
[19] A. M. Maiden, M. J. Humphery and J. M. Rodenburg: J. Opt. Soc. Am. A 29 (2012) 1606-1614.

高山　裕貴　TAKAYAMA Yuki
兵庫県立大学　大学院理学研究科
〒678-1297　兵庫県赤穂郡上郡町光都3-2-1
TEL : 0791-58-0233
e-mail : takayama@sci.u-hyogo.ac.jp