Volume 24, No.1 Pages 18 - 23

1. はじめに
　ガラス・液体・アモルファスといったいわゆる非晶質物質は結晶のような長距離秩序を有さないことから、その回折パターンはブロードなハローパターンを示し、結晶の空間群や格子定数のような記述子が存在しない。したがって、その回折パターンから原子の位置を一意的に決定することができず、非晶質物質の構造解析には規格化されたパターンをフーリエ変換することより得られる二体分布関数が古くから用いられてきた。二体分布関数はある原子から見て離れた距離に別の原子を見出す確率として定義され、非晶質の乱れた原子配列からも実空間において原子間距離、配位数といった平均化された情報を抽出することができる。そして、密度が近い結晶構造を見立ててガラスの第一近接を超えた構造（＝中距離構造）を推測することがこれまで行われてきた。このことが原因で非晶質物質の構造解析は結晶と比べて大きく立ち後れてきた。しかしながら、この問題は二体相関で議論する限りは大型放射光施設SPring-8や大強度陽子加速器施設J-PARCといった先端量子ビーム実験施設が誕生した今も変わらない。近年では、二体相関での議論からの脱却につながる電子回折の進化^[1][1] 平田秋彦、小原真司、今井英人、陳明偉：日本結晶学会誌 59 (2017) 159-165.、コヒーレントX線の利用^[2][2] P. Wochner et al.: Proc. Natl. Acad. Sci. U.S.A. 106 (2009) 11511-11514.、計算機シミュレーションと最先端数学理論との連携^[3][3] Y. Hiraoka, T. Nakamura et al.: Proc. Natl. Acad. Sci. U.S.A. 113 (2016) 7035-7040.などにより、平均化された二体相関に潜んだ非晶質物質の特徴的な構造抽出に成功した例が報告されている^[4-6][4] A. Hirata et al.: Nat. Commun. 7 (2016) 11591.
[5] S. Kohara and P. S. Salmon: Adv. Phys.: X 1 (2016) 640-660.
[6] S. Kohara: J. Ceram. Soc. Jpn. 125 (2017) 799-807.。また、最先端の量子ビーム実験施設の登場により、質の高い回折データがハイスループットで計測できるようになり、多くのデータを比較できるようになったことから、非晶質物質の構造解析はこの20年で徐々にではあるが着実に進化しつつある。

2. 本課題の目的
　本長期利用課題では、様々な非晶質物質の構造をX線回折、XAFS、中性子回折やNMRといった実験や計算機シミュレーションに加えて、逆モンテカルロモデリング（Reverse Monte Carlo, RMC）、最先端の数学理論を導入したホモロジー解析を援用することにより、非晶質物質の量子ビーム実験データおよび3次元構造データを系統的に理解することを試みた。ここでは特にガラスの短範囲構造ユニットの連結により生み出されるネットワーク、リング、ホモロジーに注目した。さらにガラスのネットワーク構造と物性の相関についても検討を試みた。

3. 研究概要
　前述の目的を達成するため、本長期利用課題では、BL01B1においてXAFS実験を^[7-9][7] L. S. R. Kumara et al.: Sci. Rep. 7 (2017) 14606.
[8] J. Han et al.: Nano Energy 49 (2018) 354-362.
[9] Y. Onodera et al.: Nat. Commun. 8 (2017) 15449.、BL04B2では高エネルギーX線回折実験を行った^[7,9,10][7] L. S. R. Kumara et al.: Sci. Rep. 7 (2017) 14606.
[9] Y. Onodera et al.: Nat. Commun. 8 (2017) 15449.
[10] 小原真司他：NEW GLASS 33 (2018) 3-7.。ここでは、（1）X線、中性子回折から得られた回折パターンの系統的な理解^[10][10] 小原真司他：NEW GLASS 33 (2018) 3-7.、（2）ZnO-P₂O₅ガラスの熱膨張係数異常の起源^[9][9] Y. Onodera et al.: Nat. Commun. 8 (2017) 15449.、（3）パーシステントホモロジーによるシリカガラスのホモロジーの抽出について述べる。

3-1 X線、中性子回折から得られた回折パターンの系統的な理解
　非晶質物質の量子ビーム実験データを系統的に解釈するため、様々な非晶質物質の回折データの比較を試みた。図1にZr₅₀Cu₅₀ガラス、アモルファスSi^[11][11] K. Laaziri et al.: Phys. Rev. Lett. 82 (1999) 3460-3463.、シリカ（SiO₂）ガラス^[12][12] http://wwwisis2.isis.rl.ac.uk/disordered/database/DBMain.htm、CCl₄液体^[13][13] H. Morita, S. Kohara and T. Usuki: J. Mol. Liq. 147 (2009) 182-185.の構造因子S(Q)を示す。横軸は原子サイズの差を規格化するために、散乱ベクトルQにS(Q)をフーリエ変換することにより得られた実空間関数の最近接距離dを乗じてある。CCl₄液体のX線回折から得られたS(Q)およびシリカガラスの中性子回折から得られたS(Q)にはQdの小さい領域にQ₁（First sharp diffraction peak, FSDP）、Q₂（Principal peak, PP）、Q₃の3つのピークが現れることが知られているが、アモルファスSiはQ₁を持たず、Zr₅₀Cu₅₀ガラスはQ₃しか持たないことが分かる。また、シリカガラスのQ₂はX線回折から得られるS(Q)には観測されないが、これはX線回折が原子番号の大きい（多くの電子を持つ）Siに敏感であるのに対して中性子回折は相対的に軽い原子であるOに特に敏感であることに起因し、O-O相関に関連したピークであるQ₂はX線回折のデータには観測されない^[10][10] 小原真司他：NEW GLASS 33 (2018) 3-7.。Zr₅₀Cu₅₀ガラスはデンスランダムパッキング構造を持ち、配位数はほぼ12である。これに対し、アモルファスSiはSiSi₄四面体、シリカガラスはSiO₄四面体、CCl₄液体はCCl₄四面体が短範囲構造ユニットとなる。アモルファスSiとシリカガラスはネットワークを形成するが、CCl₄液体ではCCl₄四面体は孤立した分子として存在する。したがって、短配位構造ユニットの中心原子から見た頂点原子の配位数と、頂点原子から見た中心原子の配位数の平均はそれぞれ、4、2.67（Siの周りのOの配位数は4、Oの周りのSiの配位数は2）、1.6（Cの周りのClの配位数は4、Clの周りのCの配位数は1）となる。すなわち図1において、上に行くほど原子のパッキングは密であり、下に行くほど疎であると言える。非晶質物質の回折パターンの1番Qの低い位置に現れるピークをFSDPと命名し、FSDP＝ガラスの中距離構造と安易に解釈している論文が多いが、実際にはQの小さい領域に現れるピークは非晶質物質によって異なってくる。我々は、FSDPは結合の手の数が異なる複数の原子から構成された多面体が疎に分布した時に多面体の面が作る秩序によって観測されるピークであると考えている^[10,14][10] 小原真司他：NEW GLASS 33 (2018) 3-7.
[14] S. Kohara et al.: Nat. Commun. 5 (2014) 5892.。また、FSDPがガラスネットワークの象徴と報告している論文も数多く見受けられるが、ネットワークを形成しても空隙がなければFSDPは消失する^[15][15] A. Zeidler et al.: Phys. Rev. Lett. 113 (2014) 135501.ことから、FSDPがガラスネットワークの象徴という解釈には慎重になる必要があることが示唆された。

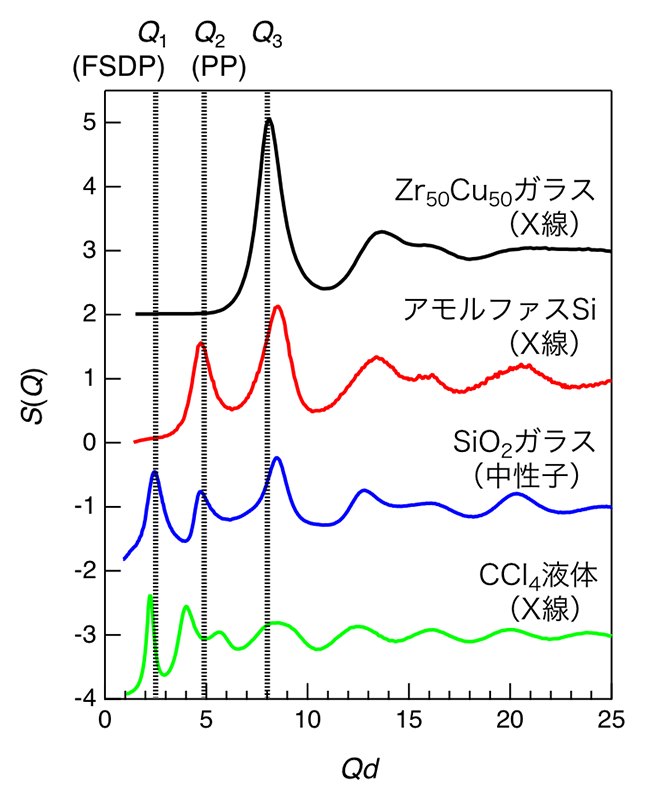
図1　Zr₅₀Cu₅₀ガラス、アモルファスSi^[11][11] K. Laaziri et al.: Phys. Rev. Lett. 82 (1999) 3460-3463.、SiO₂ガラス^[12][12] http://wwwisis2.isis.rl.ac.uk/disordered/database/DBMain.htm、CCl₄液体^[13][13] H. Morita, S. Kohara and T. Usuki: J. Mol. Liq. 147 (2009) 182-185.の構造因子S(Q)

3-2 ZnO-P₂O₅ガラスの熱膨張係数異常の起源^[9,16][9] Y. Onodera et al.: Nat. Commun. 8 (2017) 15449.
[16] 小野寺陽平他：NEW GLASS 32 (2017) 25-29.
　リン酸塩ガラスは生体関連材料^[17][17] T. Kokubo and H. Takadama: Biomaterials 27 (2006) 2907-2915.や光学材料^[18,19][18] P. I. Paulose et al.: J. Phys. Chem. Solids 64 (2003) 841-846.
[19] J. H. Campbell and T. I. Suratwala: J. Non-Cryst. Solids 263-264 (2000) 318-341.としての用途があり、最近ではエントロピー弾性を示すガラスが発見される^[20][20] S. Inaba et al.: Nat. Mater. 14 (2015) 312-317.など様々な方面に応用が期待されている。リン酸塩ガラスの特徴的な材料特性はネットワーク形成物質であるP₂O₅に対して様々なネットワーク修飾物質を適切に添加することによって得られるが、その機能発現メカニズムとガラス構造との関係はいまだに解明されておらず、リン酸塩ガラスのネットワーク構造の理解はガラス科学における重要な研究テーマの一つであった。本研究では、低融点光学ガラスの母体材料として注目されているZnO-P₂O₅ガラスを対象とし、放射光X線および中性子回折、XAFSといった量子ビーム実験とNMR実験、そしてRMC法によるモデリングを駆使してガラスの3次元構造モデルを構築し、そのネットワーク構造の解析によって熱膨張係数の組成変化に現れる異常なふるまいの起源を明らかにすることを試みた。
　今回、ガラスの組成としては、60ZnO-40P₂O₅(60ZP)および70ZnO-30P₂O₅(70ZP)を選んだ。リン酸塩ガラスのガラス形成物質であると考えられているP₂O₅は、P原子の周りに4個のO原子が配位したPO₄四面体を構造ユニットとし、O原子を隣のPO₄四面体と頂点で共有することによって3次元ネットワークを形成している^[21][21] U. Hoppe: J. Phys. Condens. Matter 12 (2000) 8809-8818.。四面体同士を繋いでいるO原子は架橋酸素と呼ばれ、ガラスネットワークを議論する際には構造ユニット中の架橋酸素の数nを指標としたQⁿという表記法が用いられる。ガラス形成物質として知られているSiO₂ガラスはSiO₄四面体の酸素がすべて架橋酸素であることからQ⁴となる。P₂O₅においてはPO₄四面体に3個の架橋酸素が存在するためQ³となる。Q³のみで構成されるP₂O₅ガラスにZnOを添加していくと、架橋酸素が切断され、非架橋酸素が増えることにより、Q²、Q¹、Q⁰が増加していく。本ガラスにおけるPO₄四面体の繋がり方に関する情報を得るためにNMR分光測定を行ったところ、60ZPガラスにおいてはQ²とQ¹がほぼ1:1で存在し、70ZPガラスにおいてはQ¹とQ⁰がほぼ2:1で存在していることが明らかになった。また、Zn K吸収端におけるXAFS測定から、Zn原子周囲のO原子の平均配位数は両組成とも結晶における配位数である4よりやや小さい値をとることが明らかになった。
　NMR分光、XAFS測定によって、本ガラスにおけるP原子とZn原子周囲の短距離構造に関する情報が得られた。本研究ではさらに、これらの短距離構造ユニットがどのような形で繋がっているのか、すなわちどのようなガラスネットワークが形成されているのかを明らかにするため、RMC法によるモデリングによってガラスの3次元構造モデルの構築を試みた。RMC法は前世紀にMcGreevyとPusztaiによって考案された手法であり、試料の密度を満たしたシミュレーションボックス内の粒子を乱数で動かすことにより実験データを再現する3次元構造モデルを構築するデータ駆動型構造モデリング法である^[22][22] R. L. McGreevy and L. Pusztai: Mol. Simul. 1 (1988) 359-367.。RMC法は原子間ポテンシャルを用いないため大規模かつ高速での構造モデリングが可能であるが、「実験データを再現する最も無秩序な構造」が得られる傾向があり^[23][23] M. T. Dove, M. G. Tucker and D. A. Keen: Eur. J. Mineral 14 (2002) 331-348.、「得られる構造は唯一の解とならない」ことに注意する必要がある^[24][24] R. L. McGreevy: J. Phys. Condens. Matter 13 (2001) R877-R913.。本研究ではZn、P原子に敏感なX線回折、比較的軽いO原子に敏感な中性子回折、Zn原子周囲のみの構造情報を持つEXAFSのデータを使用し、さらに、NMRによって得られたガラス中のQ⁰、Q¹、Q²、Q³の存在比率を再現するように構造を拘束することによって、より信頼性の高い構造モデルを構築するRMC法によるモデリングを試みた。中性子回折実験から得られた構造因子S^N(Q)^[25][25] K. Suzuya et al.: J. Non-Cryst. Solids 345-346 (2004) 80-87.、放射光X線回折実験から得られた構造因子S^X(Q)、EXAFS実験から得られたk³χ(k)に対するRMC法によるモデリングの結果を図2に示す。これより、RMC法によって得られた60ZPおよび70ZPガラスの3次元構造モデルはQⁿ分布を再現する構造拘束下ですべての実験データを良く再現していることが分かる。

図2　ZnO-P₂O₅ガラスの中性子回折(a)、X線回折(b)の構造因子S(Q)およびZn K吸収端のk³χ(k) (c)。黒：実験データ、赤・青：RMCモデル

　RMC法によって得られた60ZPガラスおよび70ZPガラスの3次元構造モデルを解析し、ZnOの添加に伴うネットワーク構造の変化を調べた。まず、PO₄四面体の連結性について調べたところ、図3に示すような結果が得られた。図において、横軸にはPO₄四面体により形成されるP_nO_3n+1ユニット内のP原子の数を、縦軸にはそのユニットに属するすべての原子数をプロットしている。図3(a)より60ZPガラスにおいては300個近いPO₄四面体(Q²)が長い鎖状ネットワークを形成していることが明らかになった。一方、70ZPガラスについては図3(b)に示すように孤立したPO₄四面体(Q⁰)とP₂O₇二量体(Q¹)のみが存在するため、PO₄四面体によるネットワークが形成されていないことが分かる。図4にZn-O結合によって形成されるネットワーク構造を調べた結果を示す。図3と同様に、図4において横軸にはZn-O結合によって形成されるZn_xO_yユニット内のZn原子の数を、縦軸にはそのZn_xO_yユニットに属するすべての原子数をプロットしている。図4(a)に示すように、60ZPにおいてはZn-O結合から形成されるZn_xO_yユニットは短く、ネットワークが形成されていないことが分かる。一方、図4(b)に示すように70ZPガラスにおいてはZnO₃、ZnO₄といった構造ユニットが中心となり、350個もの多面体が頂点および稜共有によって一つに繋がったZn_xO_yネットワークが形成されていることが明らかになった。

図3　60ZPガラス(a)、および70ZPガラス(b)におけるPO₄四面体ネットワーク

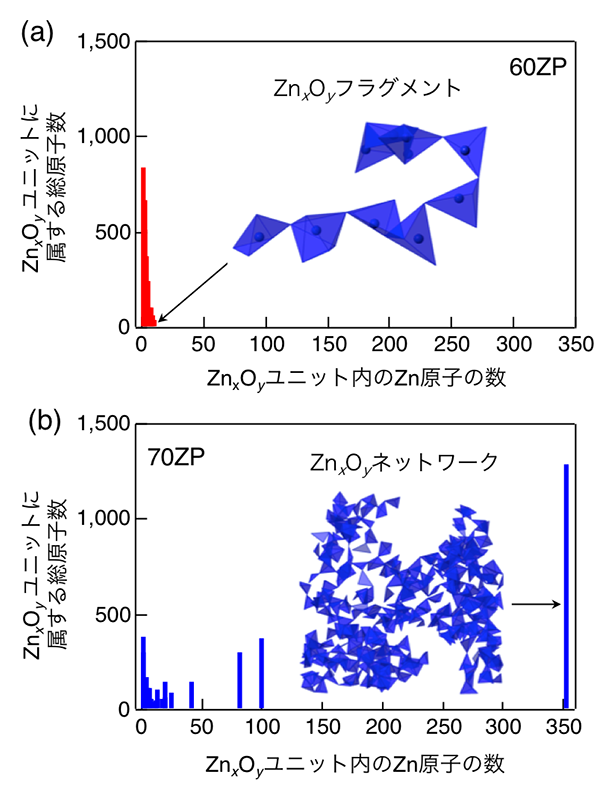
図4　60ZPガラス(a)、および70ZPガラス(b)におけるZn-O多面体ネットワーク

　60ZPおよび70ZPガラスの3次元構造モデルの解析により、ZnOが少ない60ZPガラスにおいてはPO₄四面体がネットワークを作っているのに対し、ZnOが多い70ZPガラスではそれに代わってZnO_x多面体（x = 3, 4）がネットワークを形成していることが分かった。一般に、ガラスネットワークが組成とともに変化しないのであれば、低いガラス転移温度T_gのガラスほど高い熱膨張係数を示すことが知られている^[26,27][26] M. Tomozawa et al.: J. Non-Cryst. Solids 56 (1983) 343-348.
[27] J. E. Shelby: J. Am. Ceram. Soc. 66 (1983) 225-227.。しかし、本ガラスにおいてはZnO量の増加に伴って熱膨張係数がT_gとともに上昇しており、一般的なガラス系にはない異常な傾向を示すと結論付けられた。この60ZPから70ZPへの10 mol%のZnO添加量の違い（5%のZn原子分率の上昇）によって生じるガラスのネットワークの担い手の交代が、本ガラスにおける熱膨張係数がT_gとともに上昇するという異常なふるまいと関連していることが本研究によって明らかになった。

3-3 パーシステントホモロジーによるシリカガラスのホモロジーの抽出
　シリカガラスは典型的なガラス形成物質でかつ地球科学の分野でも重要であることから、その構造物性については高温・高圧まで幅広く研究されてきた。図5に、RMCと古典分子動力学計算（Molecular Dynamics, MD）のハイブリッド化モデリングにより得られたX線と中性子の構造因子S(Q)を再現する構造モデルを示す。図1に示すとおり、シリカガラスの構造因子S(Q)のQ～1.5 Å^-1（Qd～2.4 Å^-1）にFSDPが観測される。このFSDPを解析することにより、

周　期：2π/Q_FSDP ～4 Å（図5の水色破線間で青色の矢印で示された距離）

相関長：2π/dQ_FSDP ～10 Å（図5のピンク色の領域内の矢印で示された距離）

と見積もられ、空隙越しに揃った面がFSDPの起源となる中距離構造と解釈されている^[10,14][10] 小原真司他：NEW GLASS 33 (2018) 3-7.
[14] S. Kohara et al.: Nat. Commun. 5 (2014) 5892.。この中距離構造を別の角度から解釈するために、我々はパーシステントホモロジー法^[2][2] P. Wochner et al.: Proc. Natl. Acad. Sci. U.S.A. 106 (2009) 11511-11514.を導入した。本手法の詳細は文献[28,29]に解説されているので参照していただきたい。本手法のアルゴリズムは、構造モデリングやシミュレーションにより得られた3次元座標の原子の半径を同時に増大させ、隣接した原子と重なりリングが出現した点をBirth、さらに増大させリングが消失した点をDeathとしてダイヤグラムを計算することである。対角線に近いプロファイルはBirthした後直ちにDeathする寿命の短い（小さい）リングを、対角線から離れたプロファイルは寿命の長い（大きい）リングを意味する。本手法の最大の特徴は結合を定義することなく穴の形（ホモロジー）が解析できる点である。SiO₄四面体を短範囲構造とするガラスと結晶のホモロジーを比較するため、シリカガラス、α-クリストバライト、α-石英、コーサイトのSi原子のパーシステント図を図6に示す。ガラスのダイヤグラムにはDeath（縦）軸に沿って縦長のプロファイルが観測されるが、これはガラスを構成する原子がネットワークを形成していることを示しており、Deathの値が大きいほど寿命が長い、すなわちロバストな大きなリングの存在を意味する。一方、対角線付近のプロファイルは寿命の短いリングの存在を意味する。このDeath軸に沿った縦長のガラスのプロファイルに注目すると、結晶相にも同じような位置にプロファイルが観測され、α-クリストバライト、α-石英、コーサイトと高密度になるにつれて、Death値の小さい、すなわち寿命が短いリングへと変わっていることが分かる。このような縦長のプロファイルが現れることがガラスになりやすいガラスの特徴と考えられ、このプロファイルはネットワーク形成の記述子と言える。結晶の強いプロファイルに該当する構造を抽出すると、α-クリストバライトでは比較的対称性の良い6員環のみが観測されたが、α-石英においては6、8員環が、コーサイトにおいては4、6、8員環も観測され、リングの形がねじれた対称性の悪いものであることが明らかになった。シリカガラスにこれら3つの結晶相と同じDeath位置にプロファイルが広がっていることから、ガラスには密度がより高密度の結晶のホモロジーがある、つまり、α-クリストバライトと比較して、よりねじれた形のリングが存在していることが明らかとなり、これがガラスの無秩序性の象徴であると結論付けられた。

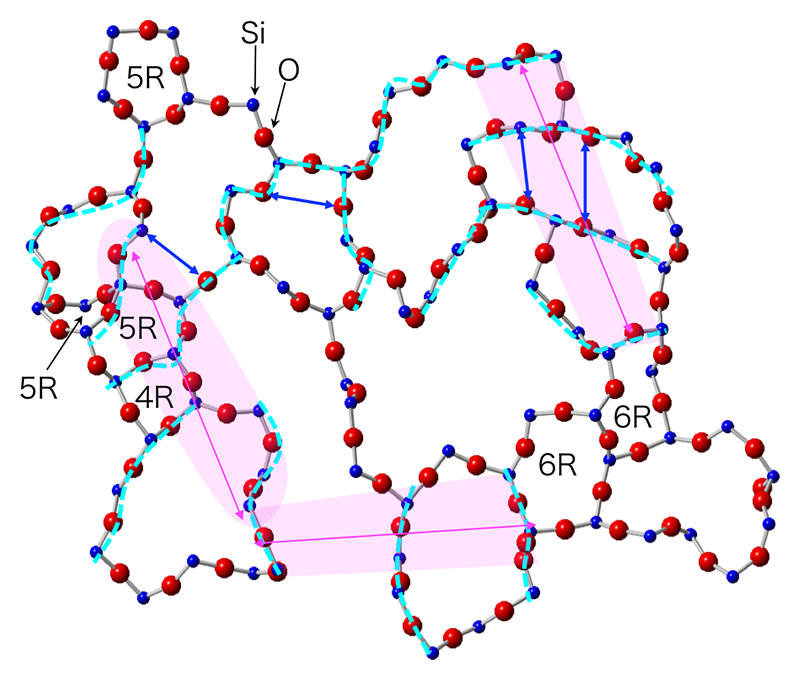
図5　RMC-MDモデリングより得られたシリカガラスの3次元構造。シミュレーションボックスを紙面方向に約9 Åにスライスした領域でネットワークを形成している原子のみ表示している。R：リング（員環）

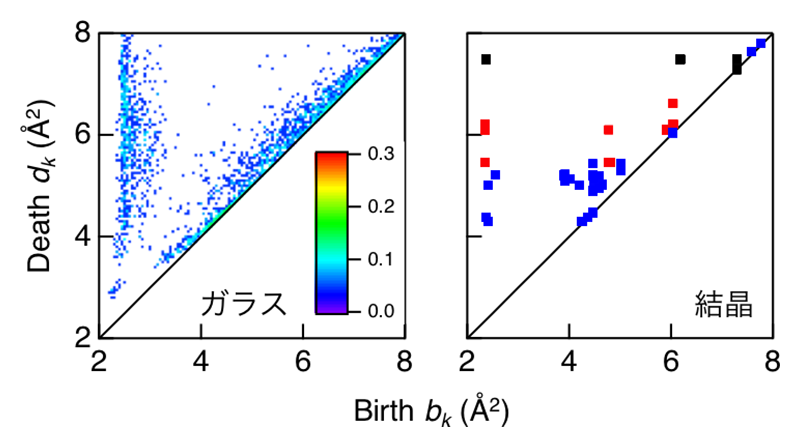
図6　シリカガラス（d = 2.2g·cm^-3）および結晶のSi原子のパーシステント図。
■：α-クリストバライト（d = 2.30g·cm^-3）、■：α-石英（d = 2.65g·cm^-3）、■：コーサイト（d = 2.92g·cm^-3）。結晶のデータは各結晶相の違いを示すため、Birth、Death点のみをプロットした。

4. おわりに
　本長期利用課題（2016A0130～2017B0130、2016A0134～2017B0134）は、BL04B2の高エネルギーX線回折計のハイスループット化からはじまり、最終的には超高温無容器融体や結晶の計測において特にスループットの向上を達成できた。そして、様々な非晶質物質の回折データを取得し、比較することにより、そのピークの由来を明らかにすることができた。また、実用により近い複雑なガラスの構造解析に取り組み、構造と物性の相関についての知見を得ることができた。さらに、逆モンテカルロ法の新しい使い方の提案や、ガラスのホモロジーの研究について新しい方向性を切り拓くことができた。
　現在、我々は企業との連携を深め、さらにデータ科学の研究者との連携の強化に取り組んでいる。本長期利用課題により、非晶質材料のマテリアルズインフォマティクスを推進する第一歩がようやく踏み出せたと言える。

謝辞
　本長期利用課題を利用した研究においては、JASRI 尾原幸治氏、伊奈稔哲氏に多大なご協力をいただいた。本稿執筆においては、高エネルギー加速器研究機構 大友季哉氏、日本原子力研究開発機構 鈴谷賢太郎氏、山形大学 臼杵毅氏、京都大学 平岡裕章氏、早稲田大学 平田秋彦氏、岐阜大学 志賀元紀氏から多大なご助言をいただいた。ここに深く感謝の意を表す。本稿で紹介させていただいた研究成果の一部はJSTさきがけ「理論・実験・計算科学とデータ科学が連携・融合した先進的マテリアルズインフォマティクスのための基盤技術の構築（JPMJPR15N4）」および科学技術振興機構（JST）のイノベーションハブ構築支援事業の「情報統合型物質・材料開発イニシアティブ（MI²I）」から支援を受け遂行した。

参考文献
[1] 平田秋彦、小原真司、今井英人、陳明偉：日本結晶学会誌 59 (2017) 159-165.
[2] P. Wochner et al.: Proc. Natl. Acad. Sci. U.S.A. 106 (2009) 11511-11514.
[3] Y. Hiraoka, T. Nakamura et al.: Proc. Natl. Acad. Sci. U.S.A. 113 (2016) 7035-7040.
[4] A. Hirata et al.: Nat. Commun. 7 (2016) 11591.
[5] S. Kohara and P. S. Salmon: Adv. Phys.: X 1 (2016) 640-660.
[6] S. Kohara: J. Ceram. Soc. Jpn. 125 (2017) 799-807.
[7] L. S. R. Kumara et al.: Sci. Rep. 7 (2017) 14606.
[8] J. Han et al.: Nano Energy 49 (2018) 354-362.
[9] Y. Onodera et al.: Nat. Commun. 8 (2017) 15449.
[10] 小原真司他：NEW GLASS 33 (2018) 3-7.
[11] K. Laaziri et al.: Phys. Rev. Lett. 82 (1999) 3460-3463.
[12] http://wwwisis2.isis.rl.ac.uk/disordered/database/DBMain.htm
[13] H. Morita, S. Kohara and T. Usuki: J. Mol. Liq. 147 (2009) 182-185.
[14] S. Kohara et al.: Nat. Commun. 5 (2014) 5892.
[15] A. Zeidler et al.: Phys. Rev. Lett. 113 (2014) 135501.
[16] 小野寺陽平他：NEW GLASS 32 (2017) 25-29.
[17] T. Kokubo and H. Takadama: Biomaterials 27 (2006) 2907-2915.
[18] P. I. Paulose et al.: J. Phys. Chem. Solids 64 (2003) 841-846.
[19] J. H. Campbell and T. I. Suratwala: J. Non-Cryst. Solids 263-264 (2000) 318-341.
[20] S. Inaba et al.: Nat. Mater. 14 (2015) 312-317.
[21] U. Hoppe: J. Phys. Condens. Matter 12 (2000) 8809-8818.
[22] R. L. McGreevy and L. Pusztai: Mol. Simul. 1 (1988) 359-367.
[23] M. T. Dove, M. G. Tucker and D. A. Keen: Eur. J. Mineral 14 (2002) 331-348.
[24] R. L. McGreevy: J. Phys. Condens. Matter 13 (2001) R877-R913.
[25] K. Suzuya et al.: J. Non-Cryst. Solids 345-346 (2004) 80-87.
[26] M. Tomozawa et al.: J. Non-Cryst. Solids 56 (1983) 343-348.
[27] J. E. Shelby: J. Am. Ceram. Soc. 66 (1983) 225-227.
[28] 平岡裕章、西浦廉政：日本物理学会誌 72 (2017) 632-640.
[29] 平岡裕章、大林一平：まてりあ 58 (2019) 17-22.

小原　真司　KOHARA Shinji
（国）物質・材料研究機構
先端材料解析研究拠点／
統合型材料開発・情報基盤部門（MaDIS）情報統合型物質・材料研究拠点（CMI²）
JSTさきがけ
〒679-5148　兵庫県佐用郡佐用町光都1丁目1-1
TEL : 0791-58-0223
e-mail : KOHARA.Shinji@nims.go.jp