Volume 13, No.1 Pages 39 - 43

1. はじめに

　物性物理に全く興味がなく耳を傾けない方でも、「ダイヤモンド」と聞くと「うん？」と振り向いてくれるでしょう。ダイヤモンドは宝石の王様として人類の歴史の中で君臨し続けていることは皆さんよくご存じのことと思います。これが固体物理のホットなテーマとなっているのだから面白いものです。ことの発端は、2004年にロシアのグループによってダイヤモンドにホウ素を高濃度に入れることによって超伝導が発見されたことに始まります^[1][1] E. A. Ekimov et al.: Nature 428 (2004) 542.。もともと純粋なダイヤモンドは良質な絶縁体ですが、ホウ素やリンを僅かに添加すると半導体的な性質を示すことが知られており、シリコン（Si）やガリウムヒ素（GaAs）などに続く次世代の高周波高出力デバイスなどへの応用が期待され世界各国で研究が進められていますので、ホウ素をダイヤモンドにドープすることは新しい試みでも何でもありません。ただ違うのは、電子デバイス目的では、キャリアーを放出する不純物であるホウ素濃度は、～10^18～19 cm^-3程度ですが、超伝導が発見されたダイヤモンドには、ボロンがその2桁以上も多く含まれていることです。それでは、この宝石の王様が、なぜ超伝導という物質科学の中でも最もホットなテーマを提供してくれたのか、その機構解明をすることにしましょう。活躍したのはX線非弾性散乱法で、BL35XUのビームラインです。

2. 超伝導のおさらい

　超伝導現象は、マイナスの電荷を持つ電子がお互いに引力を及ぼしあってペアーを作る結果として電気抵抗が完全にゼロとなる現象で、1911年にカマリン・オンネスによって水銀を絶対温度の4 Kに冷やすことによって発見されました。これは量子効果がマクロな状態として現れたものです。1950年代にこの不思議な現象を説明する理論（BCS理論：理論発表者であるBardeen，Cooper，Schriefferの3人の頭文字をとったものです。）が提唱されました。この理論は、本来反発し合うはずの電子が引力を及ぼし合ってペアーを作る原因は、結晶を構成している原子の振動（格子振動）と電子が相互作用した結果である、というもので、この機構はBCS機構と呼ばれています。超伝導現象の魅力は、超伝導体で電線を作ると電気エネルギーを全くロスすることなく全世界に配送することが可能となり、エネルギー革命が実現することです。しかし、残念なことに超伝導状態を発現させるためには低温に冷やさなければなりません。皆さんよくご存じの高温超伝導体といわれる銅酸化物でも136 Kまで冷やさなければならず、室温超伝導には程遠く固体物理の重要研究テーマの一つとなっています。

　室温超伝導体創製のアプローチとして、酸化物超伝導体などの新規超伝導体の発現機構を解明し、それを設計指針としてより高い超伝導転移温度（T_C）を示す物質合成を行う方法が考えられます。しかし、これも容易ではなく、例えば銅酸化物超伝導体が発見されて以来20年経過した今も多くの研究者の努力にもかかわらずその発現機構に関しては未だ確定した見解が得られていないのが現状です。

3. X線非弾性散乱を成功に導いたホウ素注入ダイヤモンド

　先に紹介したロシアの研究グループは、高温高圧下でホウ素を高濃度に注入したダイヤモンドを合成していましたので、様々な実験に利用される良質単結晶を得ることは困難でした。ところが、早稲田大学の川原田教授のグループは、気相合成法によって高濃度にホウ素を注入したダイヤモンド結晶作成に成功し、物質・材料機構の高野主任研究官グループによって超伝導特性が測定され、今では超伝導転移温度T_Cが11 Kのものが確認されています。気相合成法では、適当な基板を選ぶことにより単結晶作成も可能で、事実、川原田教授のグループは厚さ100 μm、面積10 × 10 mm²の単結晶作成に成功しました。これでX線非弾性散乱実験が可能となったわけです。今回のX線非弾性散乱に用いられたホウ素注入ダイヤモンドは、Si（001）の上に～1 μmのSiC、さらにその上に種結晶となる～1 μmの単結晶ダイヤモンドを成長させたものを基板として準備したものの上に成長させたものです（図1）。これで得られた単結晶の方位は、基板に垂直な方向がダイヤモンドの（001）方向になります。この結晶のT_Cは、超伝導オンセットで6.4 K、超伝導ミッドポイントで4.2 Kです^[2][2] M. Hoesch et al.: Phys. Rev. B 75 (2007) 140508(R).。

図1　CVDで作成されたダイヤモンド超伝導体の単結晶薄膜

4. X線非弾性散乱による格子振動観察^[2][2] M. Hoesch et al.: Phys. Rev. B 75 (2007) 140508(R).

　なぜ格子振動に注目したのかは、超伝導のおさらいの章で述べたことで納得していただけると思います。超伝導発現がBCS機構であれば、格子振動が電子ペアーの糊付けの役目を果たしていますので、格子振動を観測すればそれに糊付けの証拠が現われているはずです。このことは、我々の銅酸化物高温超伝導体や^[3,4][3] T. Fukuda et al.: Phys. Rev. B 71 (2005) 06050(R).
[4] K. Ikeuchi et al.: J. J. Appl. Phys. 45 (2006) 1594.、A. Q. R. BaronらのMgB₂^[5][5] A. Q. R. Baron et al.: Phys. Rev. Lett. 71 (2005) 197004.のX線非弾性散乱実験で議論されています。

　X線非弾性散乱実験は、共用ビームラインBL35XUで行いました。このビームラインは、エネルギー分解能が数meVを達成しており、ビーム強度を考慮すれば世界最高性能を持っています。今回の実験では、入射X線エネルギー15.82 keV、エネルギー分解能6.4 meVの条件で測定を行いました。測定した試料は、3.で説明したT_Cが4.2 Kの超伝導ダイヤモンドと、参照試料として同じく気相合成法で作成した窒素が注入されたダイヤモンド単結晶です。窒素が入ったダイヤモンドを参照試料とした理由は、気相合成法で作成した試料固有の影響を排除するためです。これの電気特性は純ダイヤモンドと同じく絶縁体で、格子振動も純ダイヤモンドと変化ないことを確認しています。

　格子振動は、①それが進む方向と②その大きさ（これらを波数ベクトルで表し、振動の波長の逆数に比例する量で運動量ともいう）、③振動の固有分極ベクトル及び、④そのときのエネルギーの四つの要素が決まれば状態が決定されます（格子振動の分散関係といいます）。我々は、ダイヤモンドの格子振動の中で最もエネルギーの高い縦波光学振動モード（LO―モード）に注目し、超伝導を示さない非超伝導ダイヤモンド（先に述べた窒素入りダイヤモンド）と超伝導ダイヤモンドのLO―モードの分散関係を観測し比較しました。図2に観測されたX線非弾性散乱スペクトルの例を示します。横軸は入射X線がダイヤモンドの格子振動を励起することによって失ったエネルギー、縦軸は散乱されたX線の強度です。図のΓ点というのは逆格子の原点にあたるもので、格子振動の運動量がゼロの点に相当します。また、X―点、L―点はそれぞれ［00ζ］方向、［ζζζ］方向の逆格子空間でのゾーン境界点を意味しています。散乱強度は、試料方位と入射、及び散乱X線との幾何学的な関係で決まるファクターがあるため、今回の実験配置では、縦波振動モードしか観測されないものになっています。ただし、L―点では横波振動モードも観測でき、図2c）にそれを示しています。TA、TOはそれぞれ横波音響振動モード、横波光学振動モードです。ここで注目したいのは、立方体のダイヤモンド構造の対角線方向（［ζζζ］方向）と向かい合う面方向（［00ζ］方向）のそれぞれのLO―モードのΓ点でのエネルギーです。超伝導ダイヤモンドのエネルギーが非超伝導ダイヤモンドのそれと比較して低くなっているのが観測されている（ソフト化している）のが解るでしょう。Γ点でのLO―モードの実空間での原子の動きを示したのが図3で、コーナー原子と中央に位置する原子が同じ方向に、それらの中間に位置する原子は反対方向に動く振動です。このエネルギーの低下は運動量が大きくなるにしたがって（X―点やL―点に向かって）小さくなっていっていることも観測されています。さらにスペクトルのピーク幅に注目しますと、Γ点で超伝導ダイヤモンドのピーク幅が非超伝導ダイヤモンドに比べて広くなっていることも観測されています。これらをまとめたのが図4です。横波光学振動モードもL―点で少しソフト化しているようです。しかし、音響振動モードはほとんどソフト化していません。格子振動がソフト化することや、ピーク幅が広くなることは、その格子振動モードが電子と強く相互作用している（電子―格子相互作用が強い）ことを意味しており、これらの実験事実から電子が最高エネルギーの縦波光学振動モードと強く相互作用をしてこれが超伝導発現の引き金になっていることが予想されます。あるモデルで定義される電子-格子相互作用の強さに対応する量λ（q）（qは格子振動の運動量）を、今回の実験データと電子状態計算から得られるフェルミエネルギーやそこでの電子状態密度の値を利用して計算することができ、それを図4(c)に示しています。これもソフト化が観測されている運動量領域でλ（q）が大きくなっていることがわかります。

　ここまでをまとめますと、ホウ素注入ダイヤモンドの超伝導発現は、約160 meVという非常に高いエネルギーの縦波光学振動モードが電子間に引力を与える働きをしており、超伝導状態を安定化させていることが示唆され、基本的にはBCS機構が働いていると結論できるでしょう。（横波光学振動モードもL―点で縦波光学振動モードと同程度にソフト化しており、このモードも超伝導発現に重要な働きをしていることが予測されます。）

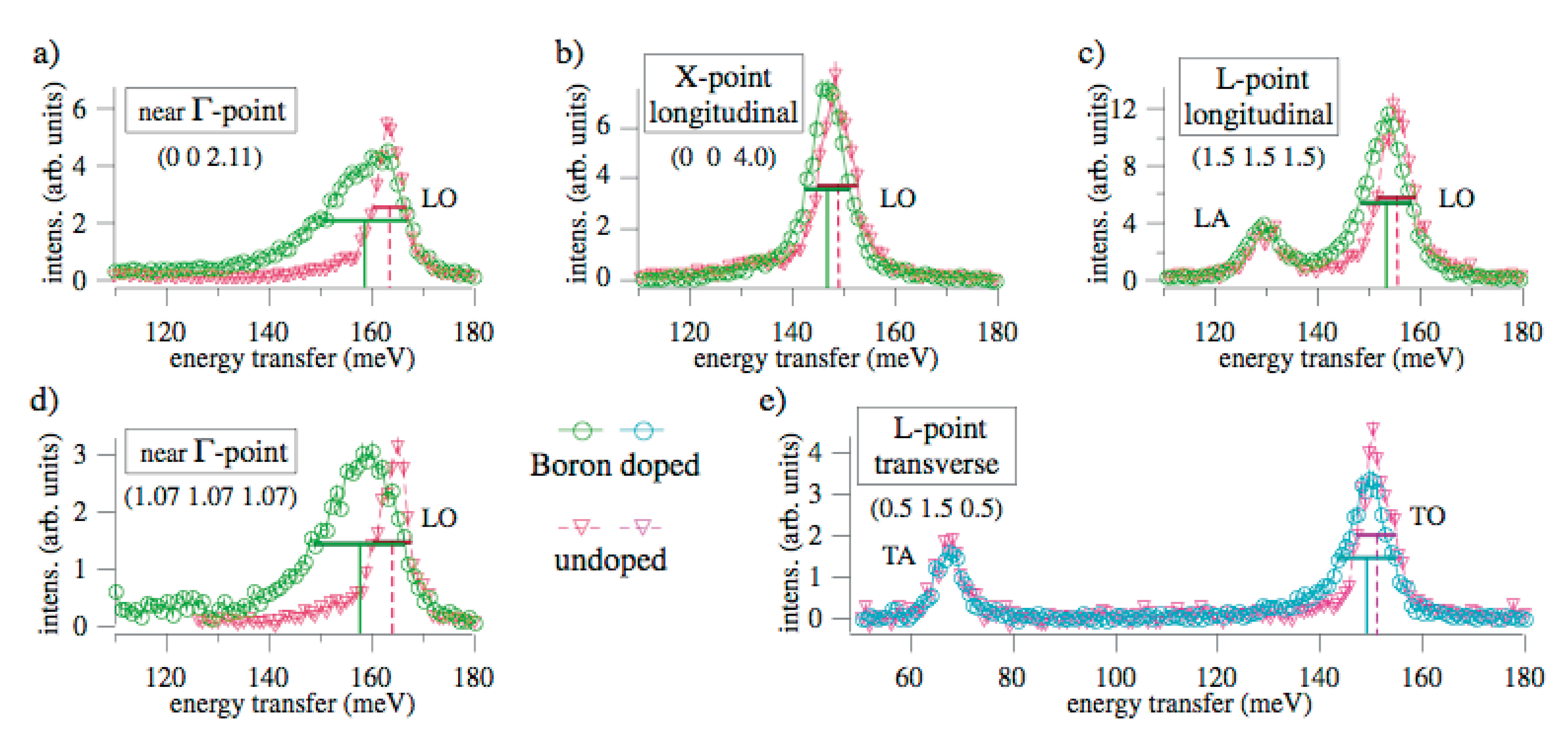
図2　非弾性X線散乱スペクトル。a)、b)は［001］方向に進む格子振動のそれぞれゾーン中心近傍、ゾーン境界、c)、d)は［111］方向に進む格子振動のそれぞれゾーン境界、ゾーン中心近傍のスペクトル。スペクトルで緑は超伝導体、赤は非超伝導体のもの。e)はゾーン境界での横波格子振動成分のスペクトル。

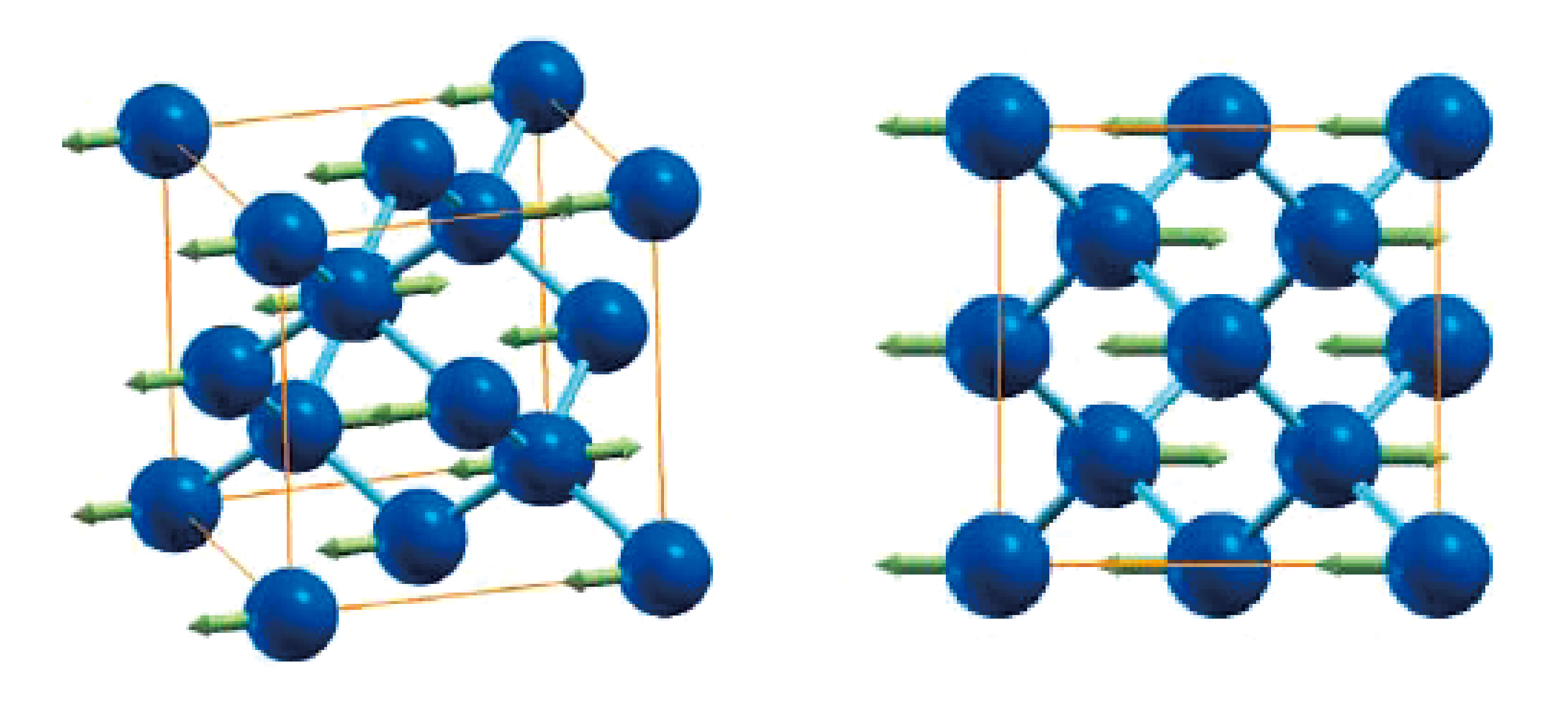
図3　ダイヤモンドの160 meV近傍のゾーン中心点（Γ-point）における縦波光学モード（LO-モード）の実空間での動きを表している。左は3次元表現、右は（100）面での投影。

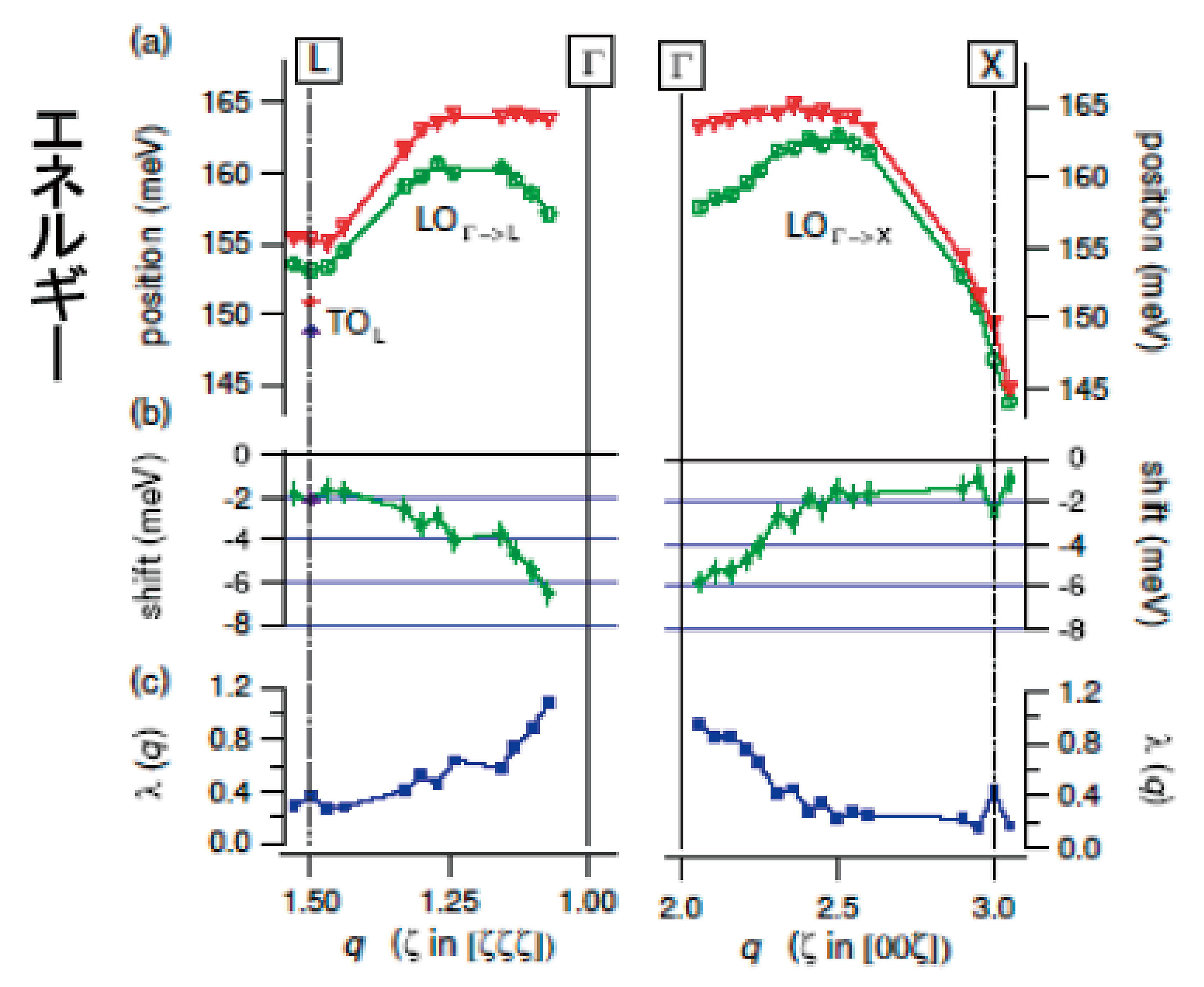
図4　(a) 緑色、赤色はそれぞれ超伝導体、非超伝導体の最も高いエネルギーを持つ縦波光学振動モード（LO-モード）の分散関係、(b) ソフト化の程度（超伝導体のLOのエネルギー マイナス 非超伝導体のLOのエネルギー）、(c) 実験データから計算された電子 - 格子相互作用。

5. ダイヤモンドで室温超伝導は可能？

　ダイヤモンドが高いエネルギーの格子振動を持っているのは、ダイヤモンドは一番安定で、かつ硬い物質であるという性質によっています。今回の実験研究で、ダイヤモンドの超伝導発現は他の物質にはない高いエネルギーの格子振動の働きによることがわかりました。それでは、ダイヤモンドを使えば今までにない高い温度で超伝導になる!?という期待を持っていいのでしょうか。期待が持てる事実としてホウ素注入量の「低さ」が挙げられます。1.で半導体デバイスの場合と比較すると2桁も多い不純物であるホウ素が注入されていると述べましたので矛盾したことをいっているように思われるかもしれません。しかし、高温超伝導体として発見以来20年以上が経過した今も研究が盛んにおこなわれている銅酸化物は、モット絶縁体にキャリアーを注入して超伝導が発現していますが、この注入量に比べてダイヤモンドの場合は1桁以上も低い注入量で、最高11 KのT_Cを示す超伝導体が創成されています。キャリアー数で規格化すると「高温超伝導体」の仲間入りです。T_Cを上げるためにもっとホウ素を注入できないものでしょうか。そこで電子状態がどのようになっているか大変気になります。T. Yokoyaらは角度分解光電子分光実験を行い、フェルミ面付近の電子が占有しているバンドの形のホウ素濃度依存性を観測しています^[6][6] T. Yokoya et al.: Nature 438 (2005) 648.。彼らは、ダイヤモンドのバンド錨像が成り立つ、すなわちホウ素を注入することによってrigid band（電子状態密度分布（DOS）の形は変えずに電子が占有しているエネルギー位置を変えるモデル）的にフェルミレベルが下がってきて価電子帯を切り金属的になりこれが超伝導を発現させる電子状態であると解析しています。このような考え方に基づいた理論的な計算もあります^[7,8][7] L. Boeri et al.: Phys. Rev. Lett. 93 (2004) 237002.
[8] K. W. Lee and W. E. Pickett: Phys. Rev. B 73 (2006) 075105.。しかし、半導体物性の立場から考えますと、不純物であるホウ素を注入すると価電子帯上端から0.37 eVのところに不純物レベル（アクセプターレベル）が形成されることはよく知られています。ダイヤモンド超伝導体には、ホウ素が10²¹ cm^-3以上も注入されており、不純物レベルがバンドを形成していることが容易に予測されます。また、不純物散乱効果も大きく、rigid band的錨像が成り立つとは考えにくい舞台です。この考え方に基づいた理論的な計算が、T. Shirakawaらによってなされており、T. Yokoyaらの実験結果を半定量的に説明しています^[9][9] T. Shirakawa et al.: J. Phys. Soc. Jpn. 76 (2007) 014711.。これら2つの異なった考え方を概念図で説明したのが図5です。上がrigid band錨像、下が不純物バンド錨像です。非常に興味が持たれるのは、T. Shirakawaらの論文では、ホウ素を決まった格子位置に炭素と置換して注入する（すなわちホウ素を秩序よく注入する）ことができれば、簡単にT_Cを上げることができることを提案していることです。現状では、ホウ素を10²¹ cm^-3以上の高濃度に注入することも大変困難な技術ですが、その上、ホウ素をダイヤモンドの格子に秩序よく注入するなんて無理だと思うでしょう。私もそう思います。が、原子を一層一層制御して結晶を作ることができるMBE法やCVD法が、今では当たり前のように研究室、産業界で活躍しています。これらの技術が開発される以前には、「それは無理」と思われていたに違いありません。ですから結晶作成技術が進歩し、もし前述した結晶が創成され、しかも理論的な予測が正しければ「室温超伝導体」も夢でなくなるかも知れません。

図5　電子状態密度のエネルギー依存性の概念図。a) rigid bandモデル、b) 不純物バンドモデル、横軸はエネルギーでフェルミエネルギー（E_F）を原点にしている。縦軸は電子状態密度（DOS）を表している。

　なお、この研究は、福田竜生（原子力機構）、竹之内智大（早稲田大）、川原田洋（早稲田大）、高野義彦（物質・材料研究機構）、長尾雅則（物質・材料研究機構）、A. Q. R. Baron（JASRI/理研）、筒井智嗣（JASRI）、J. P. Sutter（JASRI、現：DIAMOND）らとの共同研究によってなされたものです。

参考文献

[1] E. A. Ekimov et al.: Nature 428 (2004) 542.

[2] M. Hoesch et al.: Phys. Rev. B 75 (2007) 140508(R).

[3] T. Fukuda et al.: Phys. Rev. B 71 (2005) 06050(R).

[4] K. Ikeuchi et al.: J. J. Appl. Phys. 45 (2006) 1594.

[5] A. Q. R. Baron et al.: Phys. Rev. Lett. 71 (2005) 197004.

[6] T. Yokoya et al.: Nature 438 (2005) 648.

[7] L. Boeri et al.: Phys. Rev. Lett. 93 (2004) 237002.

[8] K. W. Lee and W. E. Pickett: Phys. Rev. B 73 (2006) 075105.

[9] T. Shirakawa et al.: J. Phys. Soc. Jpn. 76 (2007) 014711.

Moritz Hoesch

（独）日本原子力研究開発機構　量子ビーム応用研究部門

放射光科学研究ユニット（現：ESRF）

水木　純一郎　MIZUKI Jun'ichiro

（独）日本原子力研究開発機構　量子ビーム応用研究部門

放射光科学研究ユニット長

〒679-5148　兵庫県佐用郡佐用町光都1-1-1

TEL：0791-58-2635　FAX：0791-58-0311

e-mail : mizuki@spring8.or.jp