Volume6 No.2

背景と研究目的：

　近年の環境負荷低減の観点から飲料缶等で用いられている缶用薄鋼板（板厚 0.3 mm 以下）の薄肉化が進行しており[1]、現在は 0.13 mm まで薄肉化が進んでいる[2]。薄肉化に伴う問題点としては、缶体強度の低下の他に、形状凍結不良が挙げられる。これは、鋼板を円筒状に加工し、端面を溶接される3ピース缶において、円筒状に曲げ加工した際に端面の重なり幅が狭くなる、もしくは重ならなくなる不具合のことである。重なり幅の変動は、次工程の溶接工程において溶接不良を発生させ、生産性を大きく阻害するため、変動を極力抑える必要がある。重なり幅の変化はスプリングバックが原因であり、スプリングバック量は主に板厚と降伏強度によって変化する。

　缶用鋼板のスプリングバック量予測では、材料を弾塑性体とした上で、曲げ加工時の材料内部のひずみ・応力分布としては、板厚中央に中立面が存在し、弾性、塑性域分布が表裏で均等であるモデルを仮定して予測が行われてきた[3]。しかし、このモデルでは実測値を正確に再現しない例も報告されている[4]。そこで本研究では、曲げ加工に伴う板厚方向のひずみ分布を放射光によるひずみスキャニング法で実測し、従来から用いられてきた仮定の妥当性を検証すると共に、簡便かつ高精度スプリングバック予測式を確立することを目的とした。

実験：

1. ひずみ分布測定

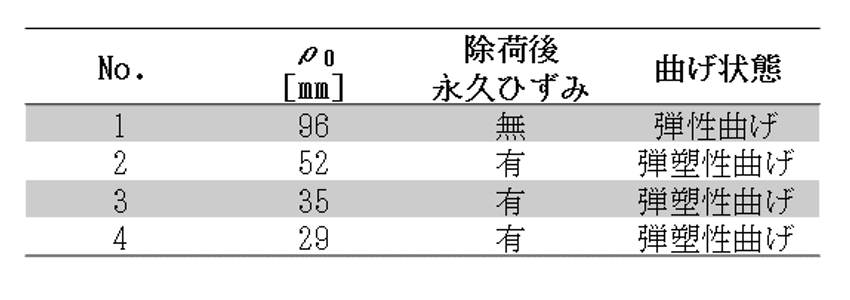
　本実験では、曲げ加工が施された状態での曲げ外周から内周までの周方向ひずみ分布を実測するため、X線ひずみスキャニング測定を以下の条件で実施した。試験片には板厚（t ）0.180 mm の低炭素鋼板（長さ 65 mm、幅 3 mm）を使用し、4点曲げ（各支点間距離 15 mm）によって曲げ加工を施した。曲げ加工は表１に示す4条件を段階的に同一試験片に対して実施した。なお、曲げ半径 ρ₀ はレーザー変位計で別途測定した。表面のひずみは、試験片の引張側表面に貼付したひずみゲージで測定した。

表１. 4点曲げ加工条件

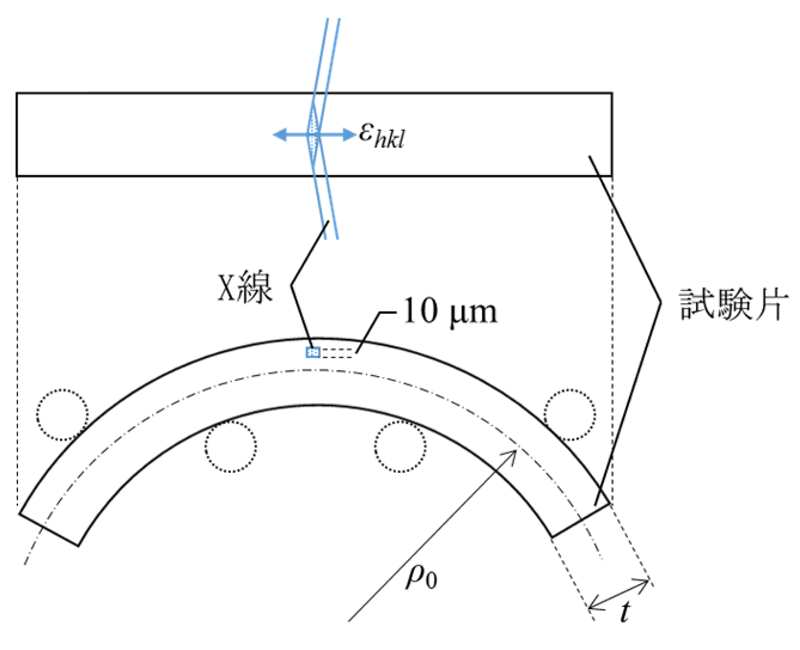
図１. ひずみ測定位置

X線ひずみスキャニング法はBL22XUで実施し、回折計はハッチ3に既設の横振型4軸回折計を用いた。測定に使用したX線のエネルギーは 70 keV、試験片前方のスリットは縦 0.01 mm × 横 0.10 mm、後方のスリットは縦 5.0 mm × 横 0.10 mm とした。曲げ頂点部の周方向ひずみは、図１に示す通りX線を試験片側面から入射し、試験片を透過して反対側から出てくる回折線をCd-Teダイオード検出器で測定し、(1)式より回折線のピークシフトを結晶格子ひずみ ε_hkl に換算して求めた。

　　　　　　　ε_hkl = －(θ－θ₀)cot θ₀　　　　　　　(1)

ここで、θ および θ₀ は曲げ加工を施した試験片および無ひずみ状態の試験片の αFe(211)の回折角をそれぞれ表し、θ₀ は 750℃ にて1時間ひずみ除去熱処理を施した試験片を用いて測定した。ステージを上下させることで板厚方向に 10 μm 間隔で周方向ひずみ分布を実測した。

2. スプリングバック量測定

　試験片には t が 0.10～0.26 mm、降伏強度 σ₀ が 240～800 MPa、ヤング率 E が 191～240 GPa の鋼板を用いた。曲げ試験には缶用鋼板で常用されるスプリングバックテスター[5]（曲げ半径 ρ₀：12.7 mm、曲げ角 θ_s：180°）を用い、スプリングバック角度 Δθ を測定した。σ₀，E は引張試験および共振法によりそれぞれ求めた。

結果および考察：

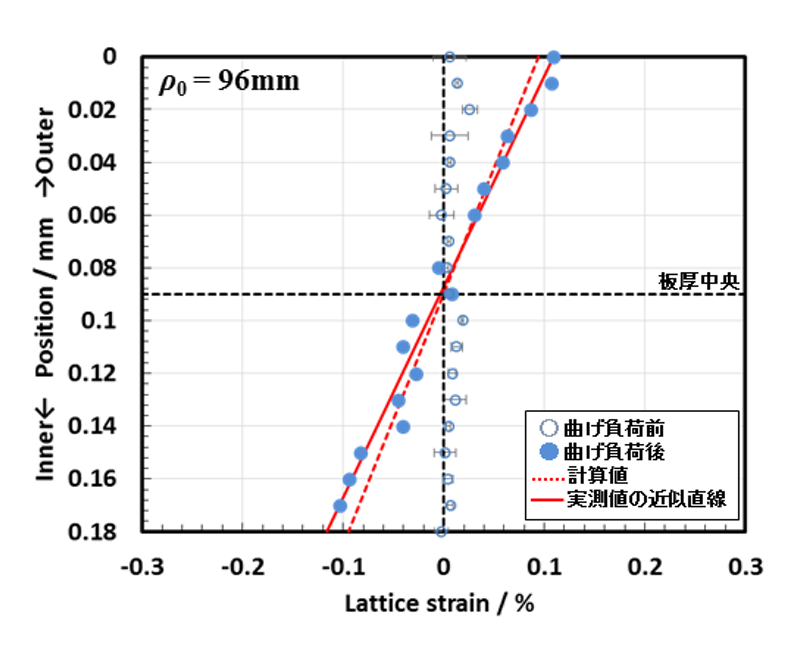
　曲げ加工前および ρ₀ = 96 mm で弾性曲げ加工を行った場合のひずみ分布を図２に示す。曲げ加工前の試験片はほぼ無ひずみ状態であり、曲げ加工を行うことでひずみ分布が直線的に変化する様子が実測できた。4点曲げの場合、試験片は同心円状に曲げられるため、板厚中央に中立面がある場合は、周方向ひずみの分布は ρ₀ に対する板厚中央からの距離によって算出することができ、図２中に破線で示した。この計算値と ε_hkl の実測値から求めた近似直線はおおむね良い一致を示し、また、ひずみゲージから求めた表面ひずみ値 0.11 % とも一致した。これらの結果から弾性曲げ加工においてはX線ひずみスキャニング法でひずみ分布を精度良く測定できると考えられる。

図２. 曲げ加工前後（ ρ₀ = 96 mm）のひずみ分布変化

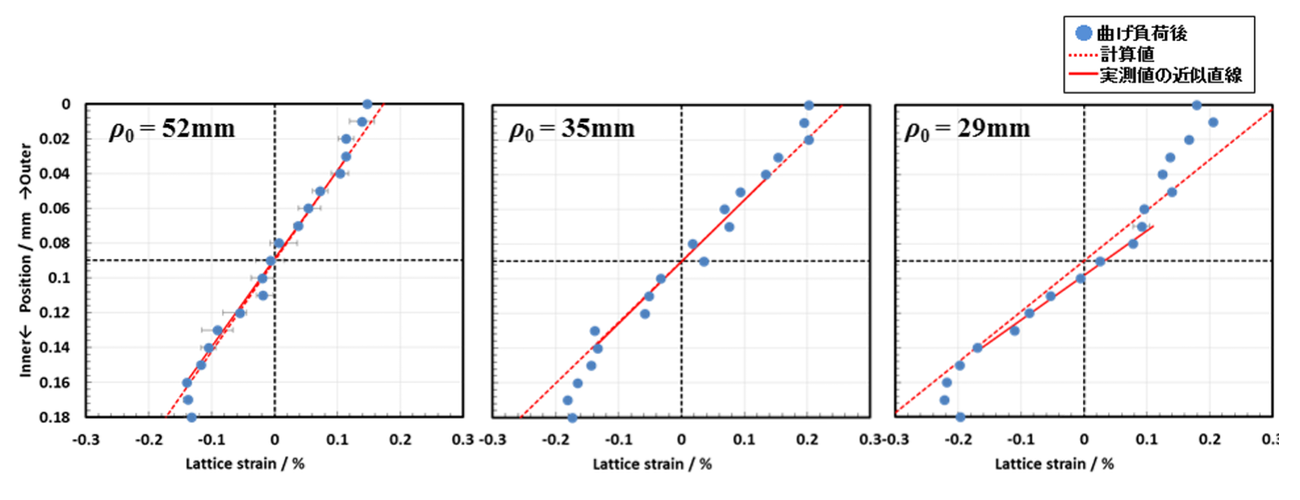
　ρ₀ = 52、35、29 mm で弾塑性曲げ加工を行った場合のひずみ分布を図３に示す。板厚中央付近の試験片内部では弾性曲げ加工と同様に直線的にひずみが変化したのに対し、内外周の表面付近ではこの直線関係から乖離する様子が確認された。ρ₀ の減少に伴い乖離領域は試験片の内部方向に拡大した。

図３. ひずみ分布に及ぼす ρ₀ の影響

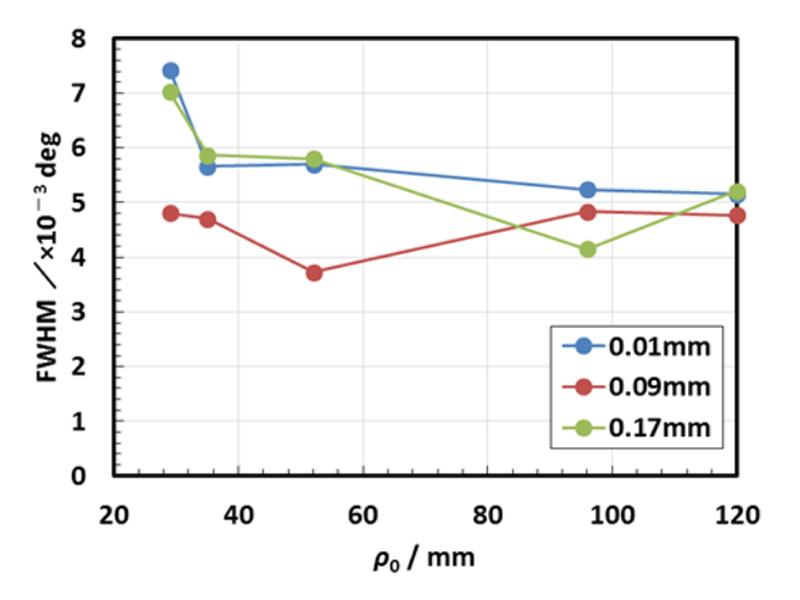
　図４に曲げ外周側表面から板厚方向に 0.01、0.09、0.17 mm の位置における回折プロファイルの半価幅と ρ₀ の関係を示す。板厚中央である 0.09 mm では ρ₀ に依らずほぼ一定の半価幅を示したのに対し、内外周の表面付近である 0.01、0.17 mm では ρ₀ が 52 mm 以下で半価幅が増大した。回折プロファイル幅は塑性変形に伴う転移の導入、その後すべり変形による結晶粒微細化によって広がる。ρ₀ = 52、35、29 mm の曲げ加工条件では弾塑性曲げ状態になっているため、表裏面から塑性変形が生じたために半価幅が増大したと考えられる。つまり、内外周の表面付近において試験片内部の直線関係からひずみが乖離する原因は、弾性限を超えて塑性域に入ったためにすべり変形が生じ、格子面間隔の広がりが限界に達したためと考えられる。X線ひずみスキャニング法で塑性変形が生じた領域のひずみ量を求めることは不可能であるが、本研究の目的である曲げ加工を行った際の板厚方向のひずみ分布、つまり中立面の位置、弾性域および塑性域の分布を明らかにすることは可能であると考えられる。

図４. 曲げ負荷に伴う半価幅の変化

　板厚方向のひずみ分布という観点で図３の結果を詳細に見ると、ρ₀ = 29 mm では無ひずみ面（=中立面）が曲げ内周側に 10 μm ほど移動し、塑性域が曲げ外周側で拡大していることが明らかとなった。

　これらの結果から、曲げ加工時の材料内部のひずみ・応力分布は板厚中央に中立面が存在し、表裏で弾性域と塑性域が均等と仮定した従来のモデルは適切ではないことが示唆された。そこで、中立面の移動および表裏で不均等なひずみ・応力分布を考慮したスプリングバック予測式を検討した。内外周で不均等な応力分布を考慮した図５の状態を仮定することにより(2)式を得た。

図５. 不均等応力分布の仮定

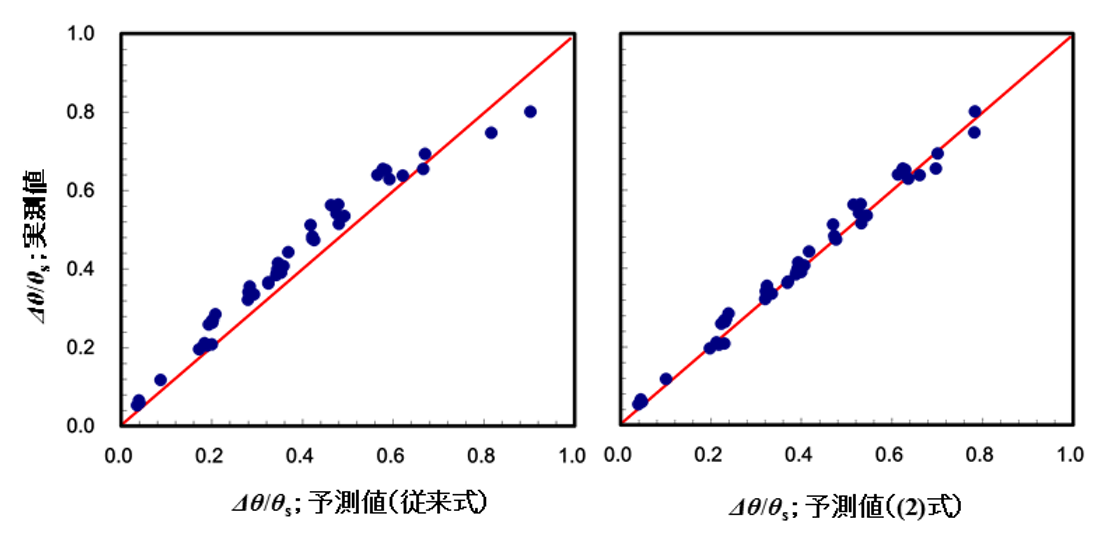
　右辺第1項が弾性成分、第2項が塑性成分である。t、σ₀、E が異なる種々の試験片のスプリングバック量測定より求めた Δθ / θ_s の実測値からαおよびβを回帰により求めると、α = 0.3、β ＝ 2.0 となった。これは中立面が曲げ内周側に位置し、曲げ外周側で塑性域が拡大することを示しており、ひずみ分布の測定結果と傾向が一致した。実測の Δθ / θ_s と従来式[3]および(2)式から算出した Δθ/θ_s を比較した図６に示されるように、従来式と比較して(2)式では t、σ₀、E が異なる種々の薄鋼板の曲げ加工に伴うスプリングバック量を精度良く再現できる。

図６. 従来式および(2)式における実測値との比較

　尚、全ひずみ理論に基づいた解析結果では ρ₀/t ＜10 で中立面移動が生じるとされているが[6]、本実験では ρ₀/t = 161 で中立面移動が生じた。本研究では確認にまでには至らなかったが、この原因として引張・圧縮における塑性流動応力の違いが影響[7, 8]していると考えられる。

まとめ：

　放射光X線回折によるひずみスキャニング法にて薄鋼板内部の円周方向ひずみ分布を実測し、曲げ半径の減少に伴い中立面が曲げ内周部に移動し、塑性域は曲げ外周側で拡大することを明らかにした。この実験結果に基づいて新たに曲げ加工に伴うスプリングバックの簡便かつ高精度な予測式を導出した。

参考文献：

[1] スチール缶リサイクル協会, スチール缶リサイクル年次レポート, 4 (2016).

[2] N. Wint, Electrochimica Acta, 203, 326 (2016).

[3] 馬場, 橋田, 鉄と鋼, 49, 507 (1963).

[4] 杉本 他, 鉄と鋼, 66, 376 (1980).

[5] 東洋鋼鈑株式会社, ぶりきとティンフリー・スチール, アグネ(東京) 124 (1970).

[6] 斉藤, 機械学会論文集, 16, 133 (1950).

[7] J. Gibmeier, M. Klaus, B. Scholtes, Materials Science Forum, 571-572, 195 (2008).

[8] 桑原, 黒田, 第52回塑性加工連合講演会論文集, 241 (2001).

ⒸJASRI

(Received: March 24, 2016; Early edition: May 30, 2018; Accepted: July 3, 2018; Published: August 16, 2018)