Volume6 No.2

背景と研究目的：

　ビームラインBL40B2は、タンパク質、合成高分子、脂質、界面活性剤などのソフトマテリアルを対象とした透過法による散乱・回折実験に用いられている[1]。広角領域から低角にいたる散乱は、分子充てん構造から分子集合体構造を捉えることができるので比較的広い分野で多くの利用がある。最近ではナノメール空間に閉じ込めた分子集合体の構造情報を得る試みが行なわれており、さらなる展開が見込まれる[2]。しかし、薄い試料を散乱体とする場合には、バックグラウンドに対し散乱体からの散乱強度が低くなりS/B比が相対的に低下する。したがって、薄膜試料からの広角領域にわたる散乱測定を高精度に行なうためにS/B比を改善する技術をBL40B2で確立する必要がある。

　バックグラウンドを低減する試みは、古くは1934年に見られる[3]。これはアモルファスなガラス材料を対象としたCu Kα線の回折実験で、空気による散乱X線の低減に真空カメラを用い実験を行っている。真空カメラは、光源を放射光に変えてもバックグラウンドの低減が期待できるが、ビームラインの保有設備に合わせた設計が必要になる。

　今回、BL40B2において最短のカメラ長 280 mmで、広角散乱計測に対応できるサンプル用真空チェンバーの開発およびその評価を行った。まず、製作した真空チェンバーの開口角が十分とられていて、散乱X線を削ることがなく、通常Qレンジと変わらずに計測が可能であることを示す。バックグラウンドと薄膜試料をテスト計測し、通常の大気圧下の結果と真空カメラの結果との比較検討を行い、今後の展開を記す。

実験：

　サンプル用真空チェンバーについて述べる。BL40B2では、検出器に 300 mm 角の２次元平面検出器を用いており、サンプルから検出器までの距離に関わる真空パスの長さを 250 mm から 6000 mm まで変更可能としている[1]。チャンバーは、最も短い 250 mm と２次元検出器サイズ、およびビーム中心を検出器中心に配置することより、散乱角でおよそ 30° を取ることが重要である。なお、サンプル交換時にチェンバーを大気圧に戻し交換することとし、サンプルの上下流にはゲートバルブを配置し真空排気容積を縮小している。チェンバーは、アルミニウムを掘り込んでゲートバルブと一体化し、開口角を広くとることを犠牲にせず、コンパクトに薄くまとめることで最短のカメラ長 280 mm を実現している（図１参照）。

図１. サンプル用真空チェンバーの設置時の様子

　広角散乱計測は、真空および通常の大気計測共にカメラ長 280 mm とし、X線波長は 0.1 nm とした。真空パスおよびサンプル用真空チェンバーの真空度は 5 Pa 以下で計測した。検出器には、R-AXIS VII (Rigaku Co., Japan)を用いた。X線フラックスは、3 × 10¹⁰ photons/secであった。試料直前のピンホールはタンタル製の直径 1 mm を用い、タンタル製ビームストップは直径 3 mm を用いた。大気圧セットアップでは、サンプル用真空チェンバーおよびピンホールケースを光軸から取り外し、代わりに大気中でピンホールおよびサンプルホルダーを利用するために水平・垂直駆動ステージ上でこれらを固定し計測に用いた。サンプル上流側のＸ線パスはピンホールの直前まで真空排気しておりＸ線を通す窓材に 1 μm 厚の窒化シリコン膜（NTT Advanced Technology Co., Japan）を用いた。一方、サンプル下流側の 250 mm の真空パスは散乱Ｘ線を通すために、窓材に開口 20 mm 角の 6 μm 厚の窒化シリコン膜（NTT Advanced Technology Co., Japan）を用いた。

結果および考察：

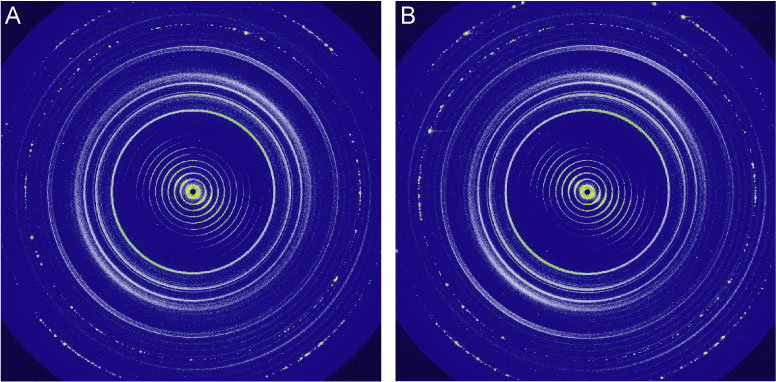
　作成したサンプル用真空チェンバーが従来の大気圧下での散乱角度領域と同等に計測できることを確認するためにベヘン酸銀を計測し、大気圧下および真空下の２次元散乱パターンを図２ＡおよびＢに示す。低角側のベヘン酸銀の１次ピークから高次散乱まで得られており、真空チェンバーがBL40B2での広角散乱計測で十分な散乱角を有していると分かる。なお、この散乱像を使用して散乱ベクトルの大きさ Q = 4π/λ sinθ （λ：波長、2θ：散乱角）が校正されている[4]。

図２. （A）大気圧下および（B）サンプル用真空チャンバーで測定したベヘン酸銀の散乱パターン

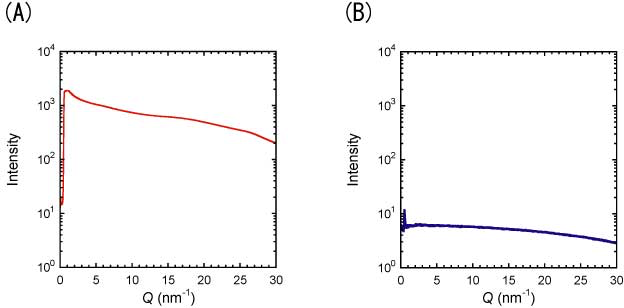
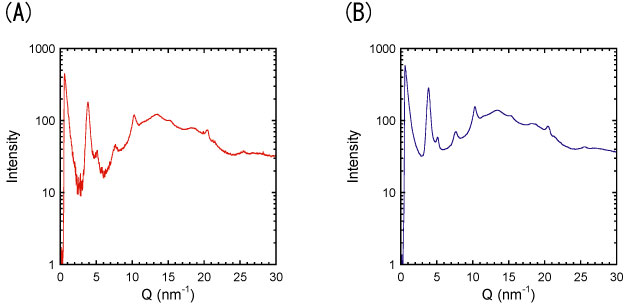
　次に、5 μm 厚のポリイミドフィルム（20EN, Du Pont-Toray Co., Ltd., Japan）およびバックグラウンドを計測した結果を示す。100秒間の露光によるバックグラウンド計測で、大気圧では数百から千程度のADU (Analog-to-digital converter unit)で（図３Ａ）、サンプル用真空チャンバーでは十ADU程度であった（図３Ｂ）。計測したポリイミドフィルムからバックグラウンドを差し引いた散乱プロファイルは、大気圧下およびサンプル用真空チェンバーで照射位置の違いによるプロファイルのバラツキを除きおよそ一致するものであった（図４ＡおよびＢ）。大気圧下で得たプロファイルは低いカウントでバラツキを示したが、サンプル用真空チェンバーではバックグラウンドがおよそ100分の１に改善されるので低いADUでもばらつきの少ない良好プロファイルが得られた。したがって、サンプル用真空チェンバーは高精度な散乱プロファイルを得るために有効であり、薄膜フィルムや繊維などを対象としたユーザー実験で利用できることを示している。

図３. （A）大気圧下および（B）サンプル用真空チャンバーで測定したバックグラウンドのプロファイル

図４. （A）大気圧下および（B）サンプル用真空チャンバーで測定しバックグラウンドを差し引いたポリイミドフィルム（厚み 5 µm）のプロファイル

　BL40B2で利用できるカメラ長は、今回計測を行ったカメラ長 280 mm だけでなく 6 m まで設定ができる。同一の２次元検出器を用いた場合、カメラ長が延びると相対的に散乱角は小さくなる。したがって、今回作成した散乱角 30° まで計測可能なサンプル用真空チェンバーは、BL40B2の全てのカメラ長で利用できることを述べておきたい。カメラ長によるバックグラウンドの大きさは、検出器１ピクセルに対するサンプルからの立体角に依存するので、カメラ長の二乗に反比例し、長ければ減少する[5]。例えば、今回の結果から１ｍのカメラ長でバックグラウンドを見積もると、同じ１ピクセルで検出するバックグラウンドはおよそ 0.08 倍の 100 秒で大気圧下では 100 ADU程度、真空チェンバーでは 1 ADU程度までの減少を見積もる。したがって、薄膜試料の散乱計測ではカメラ長によらずS/B比改善にサンプル用真空チェンバーが利用できると考えられる。

　薄膜試料の他に、一般的なバルク試料に適応した場合の期待される効果について述べる。R-AXIS VII検出器を用いた散乱計測では 1 ADU刻みとなる 14 bit のレンジ内に強度を収めることが重要である。真空チェンバーを用いたときのバックグラウンドの低減は、14 bit のレンジ内にサンプルからのシグナルをより多く積算できる効果が考えられる。例えば、100 秒間の計測では、およそ 1000~2000 ADU低減し 14 bit まで積算できたならば、10 ％ 程度強度を加算できる。カメラ長を長く設定すれば、バックグラウンドは１ピクセルに対する立体角に応じて減少するので、真空チェンバーを用いたサンプルからのシグナル積算効果が 10 ％ より減ぜられる点には留意が必要であろう。なお、サンプル用真空チェンバーを用いる場合、真空内でバルクや液体などのサンプルを扱うことになり試料準備に密閉を要するなどの手間の問題があるので、データの質の改善と実験効率を総合的に勘案することがバルク試料に対して必要であろう。

今後の課題：

本実験において、サンプル用真空チェンバーが薄膜試料に対する広角散乱計測のS/B比改善に有用であることが示された。しかし、現状ではサンプル交換のたびに真空チェンバーをリークしなければならない。今後、サンプルチェンジャーを導入し、実験効率を上げることが重要になる。

参考文献：

[1] K. Inoue et al., AIP Conf. Proc., 705, 336 (2004) or

http://www.spring8.or.jp/wkg/BL40B2/instrument/lang/INS-0000000535/instrument_summary_view

[2] S. Nakano et al., J. J. Appl. Phys., 52, 035002 (2013).

[3] B. E. Warren, Phys. Rev., 45, 657 (1934).

[4] T. C. Huang et al., J. Appl. Cryst., 26, 180 (1993).

[5] W. Benenson et al., Handbook of Physics, Library of Congress Cataloging-in-Publication Data, W. Benenson, Springer-Verlag, New York (2001) 12.

ⒸJASRI

(Received: September 14, 2017; Early edition: January 31, 2018; Accepted July 3, 2018; Published August 16, 2018)