Volume6 No.2

背景と研究目的：

　モレキュラーイメージングの分野では、光情報を利用してターゲット分子を高感度に検出する方法が主力となっている。そのなかで、低干渉光を利用して深さ方向の情報を高分解能で取得することができるOCT装置（Optical Coherence Tomography：光干渉断層撮影）が注目されている。OCTシステムは、生体組織を良く透過する赤外光の散乱光と外部の光の干渉を利用して、非侵襲に生体組織の断層画像を高分解能で取得する最先端の医療撮影技術である。

　1991年にMITより論文が発表されて以来わずか5年で眼科医療の分野で実用化され急速に普及した[1]。現在では、眼科のみならず、消化器官、肺、歯、血管壁などにその利用範囲は拡大を続けている。3次元のOCT画像を高速に取得できればその場診断が可能となり、病理組織検査を省略することができるため、患者の負担を極端に少なくすることできる。OCT装置には、FD-OCT（Fourie domain optical coherence tomography）と、SD-OCT（Spectral domain optical coherence tomography）に分類される。FD-OCTの中でも、高速波長掃引光源を用いたSS-OCT（Swept-source optical coherence tomography）は、高感度かつ高速応答なため、最も有望視されている方式である。

　近年、我々は、従来材料に比較して1桁以上高い特性を有しており、図１に示すようなぺロブスカイト構造をとる電気光学結晶 K_yLi_1-yTa_xNb_1-xO₃（KTN）を用いた光偏向器を共振器に適用し世界最速クラスのOCT用高速波長可変光源を実現した[2]。このKTN光偏向器は、電極から結晶内に注入された電子がトラップサイトにトラップされた残留電荷を利用した動作原理であることがわかっている[3]。図２に偏向の様子と電界印加の様子を示す。直方体状の加工した結晶にTi電極を取り付けDC電圧を印加することで電界方向に光が偏向する。光偏向器の性能はこの残留電荷の分布や量により支配的に決定されており、トラップサイトに興味がもたれるところである。

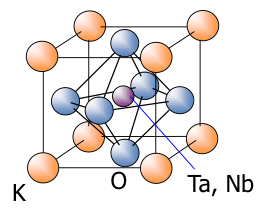
図１　KTN結晶

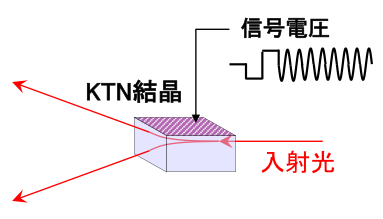
図２　KTN光偏向器

　ところが、そのトラップサイトの起源については十分解明されていない[3]。これは、トラップの濃度が 4 × 10²⁰ m^-3 と非常に微量と考えられているため通常の光学的方法では測定できないためと考えられる。今回KTN結晶をXAFSを用いて評価し、トラップサイトの起源を探索することを目的とする。結晶育成条件、Li添加量や加工条件を変えて結晶内のトラップ濃度を大きく変えたKTN結晶のXAFSを比較する。KTN結晶のトラップサイトの起源解明は、高速波長可変光源のさらなる性能向上に寄与するともに、KTN結晶材料化学の進歩につながると考えている。

実験：

　今回の全試料とも高品質な光学結晶を用いるためバルクのサンプルを用いると結晶構造由来の長距離秩序のＸ線回折によりXAFSの信号が埋没してしまう可能性が考えられた。そこで、このＸ線回折由来の信号の影響を防ぐためKT結晶、Nb₂O₅、KTN結晶を細かく粉砕した後、10 μm 径のふるいにかけて、10 μm 以下の径のみの粉体をペレット状に加工・成形した。KTN結晶の作製方法としては、Top Seeded Solution Growth（TSSG）法と呼ばれる方法で成長した[4]。結晶原料の仕込み組成として濃度として１%（以下Li濃度小）および 10%（以下Li濃度大）のLiを添加し結晶作製した。Nb : Ta の比率は 0.35 : 0.65 とした。KTN結晶のトラップ濃度については光学測定を用いて別途確認した。が高い試料ほど光学特性に優れるため[3]、光学特性を用いて選別した。

　なお、KTN結晶は温度によって様々な結晶系をとるが結晶系に応じて特性が異なるため、KTN結晶が立方晶となるように約 70°Ϲ になるように測定サンプルをヒートガンを用いて加熱してXAFS測定を行った。70°Ϲ にてKTN結晶が立方晶になることは別途ラウエカメラで確認した。BL14B2ラインを用いてKTN結晶のTa-L_III およびNb-K吸収端のXAFSを測定した。

結果および考察：

　以下の結果はすべてスプライン領域を 0～10 Å^-1 としてAthenaを用いて解析した。XAFS領域の振動のグラフを各図の(a)で示す。またフーリエ変換を k= 3～10 Å^-1 の範囲で行った結果を各図の(b)で示す。標準試料として、TaについてはKT結晶を、Nbについては Nb₂O₅ を用いた。

　最初に、Ta-L_III 吸収端の結果を図３(a)、(b)、図４(a)、(b)に示す。標準試料であるKT結晶および作製条件およびLi添加量を変えて作製してトラップ濃度が大きく異なるKTN結晶の解析結果を示した。まず、KT結晶において、1.6 Å 付近の信号は最近接のTa-Oに基づくもの、3.8 Å 付近の信号は最近接のTa-Taに基づくものと考えられた。一方、作製条件およびLi添加量を変えて作製したKTN結晶において、トラップ濃度の大小に依存するXAFSの信号の違いは明確には観測できなかった。しかし、KT結晶で観測された 3.8 Å 付近の最近接のTa-Taに基づく信号が、どのKTN結晶でも消失しているのは大変興味深い。これは、KTN結晶のTaとNbはクラスター的に配列するのではなくて、TaとNbがランダムに配列してTaの短距離秩序が失われていることによるものと考えられる。

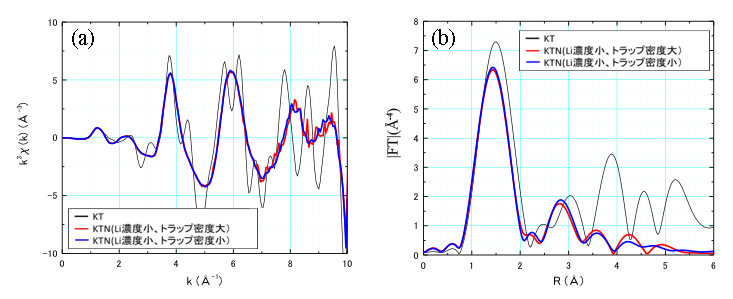
図３　KTN結晶（Li濃度小）のTa L_III吸収端のXAFS。

(a)は EXAFS振動関数、(b)は動径構造関数（黒線（KT結晶）、赤線（トラップ濃度大）、青線（トラップ濃度小））

図４　KTN結晶（Li濃度大）のTa吸収端のXAFS。

(a)は EXAFS振動関数、(b)は動径構造関数（黒線(KT結晶)、赤線（トラップ濃度大）、青線（トラップ濃度小））

　次に、Nb-K吸収端の結果を図５(a)、(b)、図６(a)、(b)に示す。標準試料である Nb₂O₅ および作製条件およびLi添加量を変えて作製してトラップ濃度が大きく異なるKTN結晶の解析結果を示した。まず、Nb₂O₅ において、1.25 Å 付近の信号は最近接のNbTa-Oに基づくもの、3.2 Å 付近の信号は最近接のNb-Nbに基づくものと考えられた。一方、作製条件およびLi添加量を変えて作製したKTN結晶において、トラップ濃度の大小で明確なXAFSの信号の違いは観測できなかった。しかし、Nb₂O₅ で観測された 3.2 Å 付近に最近接のNb-Nbに基づく信号がどのKTN結晶でも消失しているのは大変興味深い。これは、Ta のXAFSの結果で得られたことと一致し、KTN結晶のTaとNbはクラスター的に配列するのではなくて、TaとNbがランダムに配列してNbの短距離秩序が失われていることによるものと考えられる

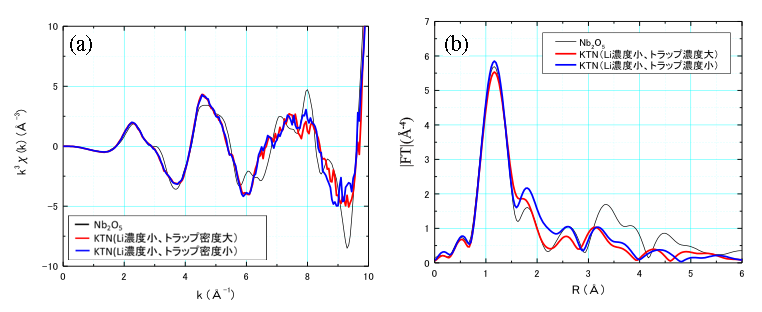
図５　KTN結晶（Li濃度小）のNb吸収端のXAFS。

(a)は EXAFS振動関数、(b)は動径構造関数（黒線(Nb₂O₅)、赤線（トラップ濃度大）、青線（トラップ濃度小））

図６　KTN結晶（Li濃度大）のNb吸収端のXAFS。

(a)は EXAFS振動関数、(b)は動径構造関数（黒線(Nb₂O₅)、赤線（トラップ濃度大）、青線（トラップ濃度小））

謝辞：

　測定に有益なコメントを頂いたNTT物性研究所（現福岡工業大学）の前田文彦博士に感謝いたします。

今後の課題：

　KTN結晶において最近接のTa-TaおよびNb-Nbの信号が弱くなっているのはTaおよびNbがランダムに配列しているためと考えている。そのランダム性を明らかにするには構造モデル計算が必要と考えられる。

参考文献：

[1] Huang D et al., Science, 254, 1178 (1991).

[2] K.Nakamura, et al., J. Appl. Phys. 104, 013105 (2008).

[3] J. Miyazu et al., Appl. Phys. Exp., 4, 115101 (2011).

[4] W. A. Bonner, et al., Ceram. Bull., 44, 9 (1965).

ⒸJASRI

(Received: March 3, 2016; Early edition: April 25, 2018; Accepted: December 18, 2017; Published: August 16, 2018)