Volume5 No.2

背景と研究目的：

　近年、地球環境保全のために自動車・航空機をはじめとする輸送機器の燃費向上のための軽量化は緊急の課題であり、この目的のための切り札の材料として繊維強化樹脂材料の実用化が進んでいる。特に自動車など陸上輸送機器では製造コストの点から炭素あるいはガラスの短繊維で強化した熱可塑性樹脂SFRP (Short-fiber Reinforced Plastics) が注目されており、繰返し荷重を受ける強度部品への適用時の安全性の確保のために、応力評価法および疲労損傷評価技術の確立が急務となっている。SFRPは異方性が非常に強く、損傷およびき裂進展挙動の評価のためには、部品の危険部における繊維配向性を考慮して応力状態を評価することが不可欠である。

本研究の目的は次の通りである。

(1) 炭素短繊維30 wt%で強化したPPS (polyphenylene sulfide) 樹脂の2相複合材CFRP (Carbon-fiber Reinforced Plastics) を射出成形した1 mm平板から、維配向が一方向に揃った表面層のみを取りだした板厚0.4 mmの表面層平板 (NSLP) に、疲労き裂を導入し、負荷応力状態でき裂近傍のひずみ・応力分布の計測を基に、き裂進展の支配力学パラメータを検討する。

(2) 実用部品に使用されているPPS、ガラス繊維、炭酸カルシウムを等量混合した3相複合材GFRP (Glass-fiber Reinforced Plastics) についても、負荷応力下で、応力・ひずみ測定を行うことから、X線応力測定法が適用できることを明らかし、ひずみ・応力評価法としてX線法の実用性を高める。

実験１：

　炭素短繊維で強化した熱可塑性樹脂CFRPのマクロ残留応力を、母相応力のX線測定から評価する手法を確立し、その有効性および実用性を高めることが目的である。

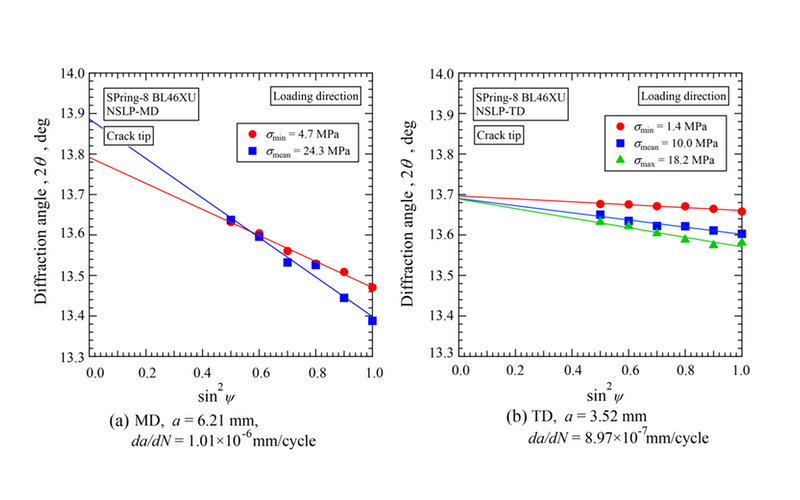
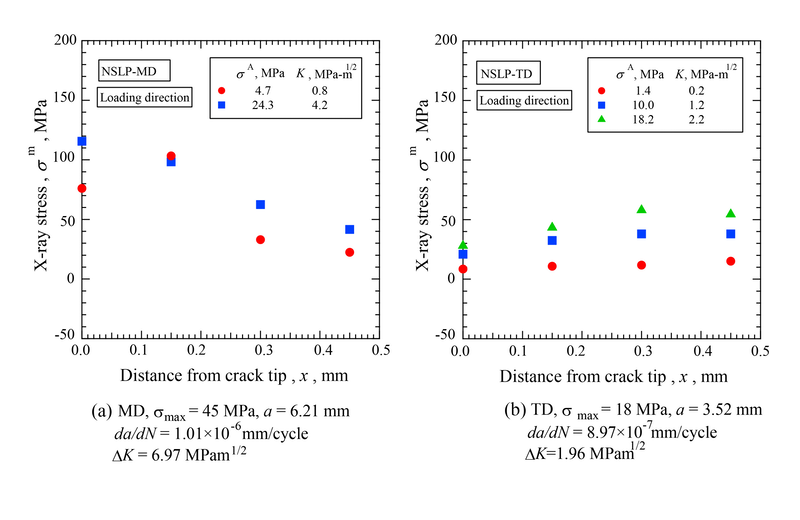
　本研究の第一の実験での試料は、CFRPのNSLPの平板試験片(長さ80 mm、幅10 mm、厚さ0.4 mm)で、これに応力比0.1の引っ張り繰り返し荷重を負荷して、疲労き裂を挿入した。試験片は繊維方向が荷重負荷方向に配向したMD材、および荷重方向に垂直に配向するTD材の2種類である。前者ではき裂は繊維に垂直に進展し、後者ではき裂は平行に進展する。また、両材料における疲労き裂は、ほぼ同一のき裂進展速度を有した状態で疲労試験を中断して、応力分布測定に供した。中断時の疲労状態は、MD材について、最大応力 σ_max = 45 MPa、き裂長さ a = 6.21 mm, き裂進展速度 da/dN = 1.01×10^-6 mm/cycle、応力拡大係数範囲 ΔK = 6.97 MPam^-1/2である。一方、TD材は、σ_max = 18 MPa、a = 3.52 mm、da/dN = 8.97×10^-7 mm/cycle、 ΔK = 1.96 MPam^-1/2である。繊維方向がき裂進行に垂直なMD材の方が、平行なTD材よりき裂進展抵抗が大きく、同一のき裂進展速度に対する応力拡大係数範囲は、前者の方が3.5倍程度と大きい。

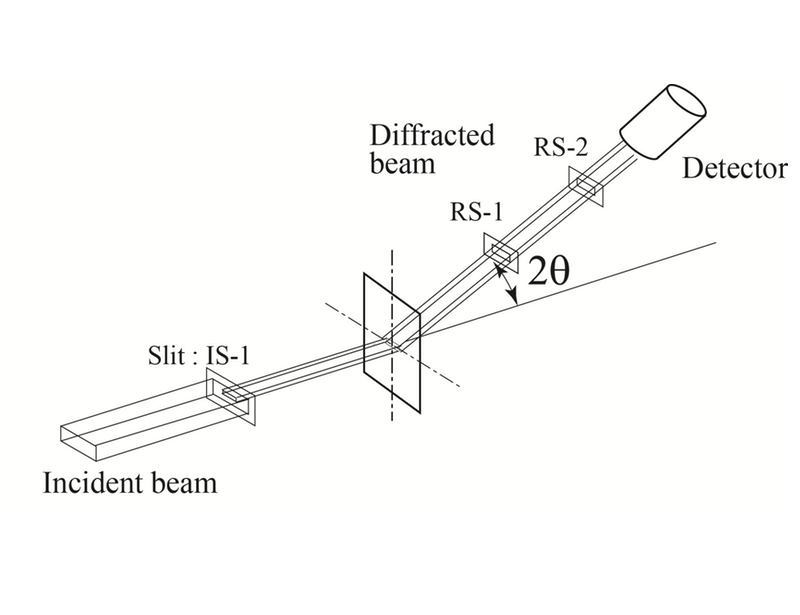
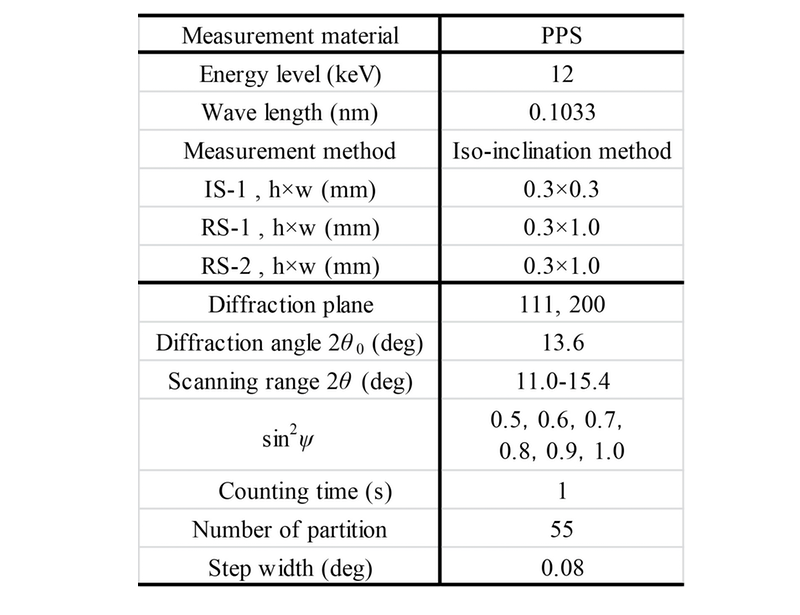
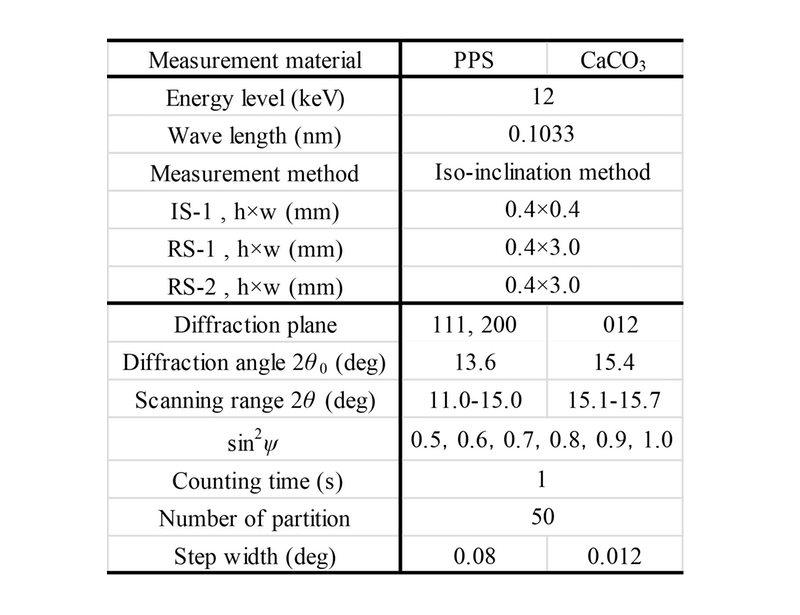
　応力測定はビームラインBL46XUにおいて、エネルギ12 keVのX線を用いて行った。Fig. 1に実験での光学系を示す。フーバー製の多軸回折系に検出器としてNaIシンチレーションカウンターを用いた。また、条件はTable 1にまとめる。本実験では、照射領域を小さくして、応力勾配を有する領域での応力分布を測定した。受光側のスリットはダブルスリットである。入射ビームを4次元スリット(IS-1；高さ0.3 mm、幅0.3 mm)で制限し、検出側はダブルスリット(RS1、RS2: 高さ0.3 mm、幅1.0 mm)とした。PPSの111、220回折のピークシフトの計測から母相のひずみを計測した。回折角は13.6°であり、応力の決定は、透過法・並傾法の光学系でsin²ψ法によって行った。sin²ψは0.5から1.0まで1.0刻みで6点の測定をした。検出器の走査角度範囲は11.0°から15.4°で、この範囲を0.08°ステップで55点分割した。計測時間は1sである。なお、スリットの寸法は一定で測定したので、sin²ψの値によってX線の照射領域は異なる。

　疲労き裂を導入したNSLPの平板試験片に、疲労荷重と同様に引張荷重を負荷した状態で、き裂近傍について荷重方向の応力分布を計測した。なお、応力測定で使用するPPS相のX線的弾性定数は、同一材料について実験室X線で測定した値を用いた[1]。X線的弾性定数は、PPSのみで射出成形した平板に曲げ負荷装置で応力負荷し、反射法・側傾法のsin²ψ法によって測定した。

実験１の結果および考察：

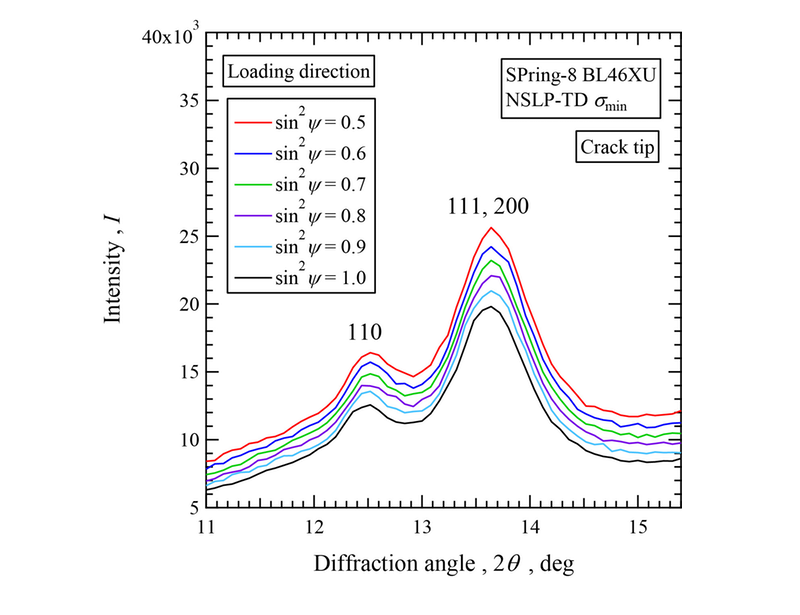
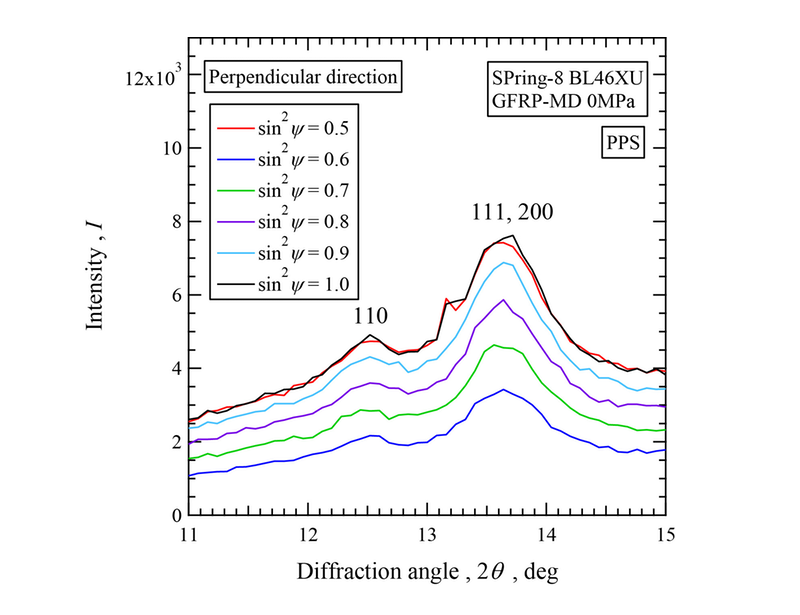
NSLPのTD材に対して得られたプロファイルの例をFig. 2に示す。疲労繰返しの最小応力 σ_min ( = 1.4 MPa ) を負荷した状態で、き裂先端での荷重軸方向の応力を、sin²ψ法で測定するために計測したプロファイルである。このプロファイルは全てPPS(斜方晶)からの回折であり、炭素繊維からの回折は含まれていない。低角から110、200、111の回折に対応する。ここで、(1)LP因子の補正、吸収因子補正、(2)平滑化、(3)バックグラウンド除去、(4)回折プロファイルをGauss関数によりフィッティングにより回折角を求めた。その際、200、111を一つのピークとして、110のピークと波形分離を行った。

　Fig. 3には負荷状態でのMD材、およびTD材におけるき裂先端での負荷荷重方向のPPS相の軸方向応力に対するsin²ψ線図を示す。また、Fig. 4にはこれから得られた軸方向応力の分布を示す。MD材では2応力レベル、TD材では3応力レベルでの測定結果である。ここで、まず負荷応力が疲労試験で負荷した最小応力における測定結果(図中の赤丸印)において、TD材では10から20 MPa程度の低い値であり、ほぼ一定であるのに対して、MD材では特にき裂近傍で100 MPa程度の大きな値となっている。これは、MD材では負荷状態でのき裂近傍での繊維の引き抜けなどにより、母材に大きな引張が残留していることに起因すると考えられる。一方、TD材では繊維の引き抜けはなくき裂近傍での変形により母相の残留応力が負荷されることはない。

Fig. 1 Experimental set-up.

Table 1 Measurement condition for NSLP of CFRP.

Fig. 2 Diffraction profiles of PPS from TD specimen of NSLP of CFRP for different sin²ψ.

Fig. 3 2θ-sin²ψ diagram taken at crack tip in MD and TD specimens of NSLP of CFRP.

Fig. 4 Stress distribution near crack tips in MD and TD specimens of NSLP of CFRP.

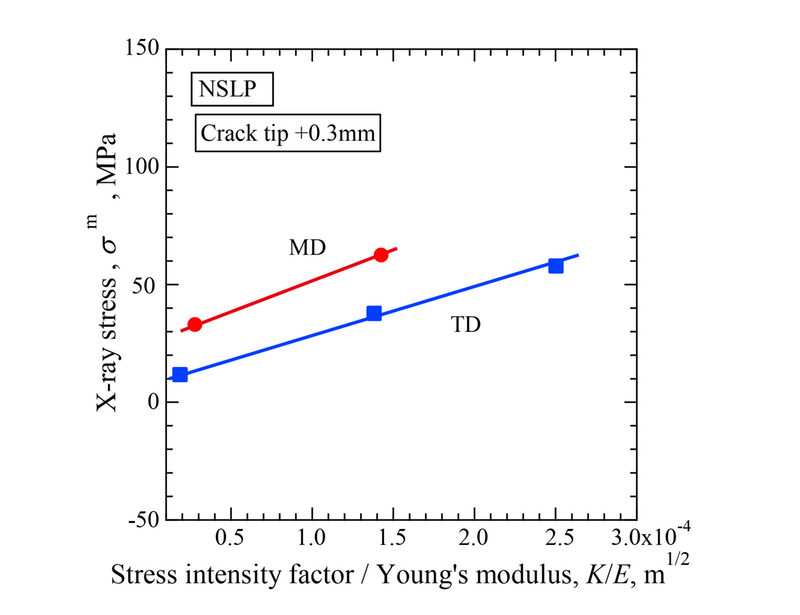
　負荷応力が増すと母相応力も増大する。MD材およびTD材ともに負荷応力の増大とともに母相応力は増大するが、き裂先端近傍での上昇量が特に大きいということはない。ここで、き裂先端から0.3 mm 位置での荷重軸方向の母相応力と、負荷した応力拡大係数ΔKをヤング率Eで割った値ΔK/Eとの関係をFig. 5に示す。ここで、非常に興味深い点は母相応力の増加量と、ΔK/Eとの関係には繊維配向はあまり影響しないことがわかる。一方、繊維配向が異なったTD、MD 材における疲労き裂進展速度 da/dN が、同一ΔKではMD材の方が非常に遅くなるが、ΔK/Eで整理するとほぼ同一となることを明らかにした[2]。このこととFig. 4に示す結果はよく対応する。つまり、き裂先端近傍の変形挙動はKではなく、ΔK/Eによって決定されることを意味しており、これがき裂進展速度を支配するパラメータであることを支持する実証データであると見なされる。

　今後、荷重条件が異なるき裂に対しても同様の測定を行い、蓄積されたデータを基に支配力学パラメータとしての有効性の確認が必要である。

Fig. 5 Change crack-tips stress with stress intensity range divided by Young's modulus of MD and TD specimens of NSLP of CFRP.

実験２：

　対象とする材料はPPS、ガラス繊維、炭酸カルシウムを各33 wt%混合したGFRPの射出成形板である。実際の部品は6 mm厚さで成形されている。しかし、設定したエネルギ12 keVでは、透過X線強度が低く、測定に長い時間がかかることが予想されたために、予定を変更して、まず1 mm厚さの平板（長さ50 mm、幅10 mm）を用いて、引張負荷条件下で応力測定を行い精度について検討することとした。試験片としては、CFRPと同様に荷重方向が射出方向に平行なMD材と垂直なTD材について測定した。 Table 2に条件をまとめる。光学系はCFRPの場合と同一である。PPSの111、220回折のピークシフトの計測から母相のひずみを計測した。応力の決定は、透過法・並傾法の光学系でsin²ψ法によって行った。本実験では、照射領域を0.4×0.4 mm²と大きくして、回折X線強度を上げた。また、炭酸カルシウムも結晶であり、この相の応力測定も検討した。透過法・並傾法の光学系でのsin²ψ法によって行った。

実験２の結果および考察：

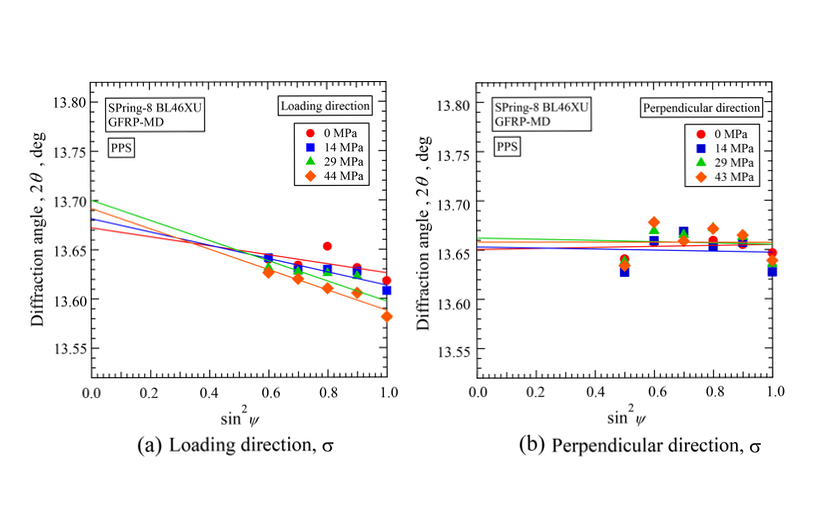
　GFRPのMD材から得られたプロファイルの例をFig. 6に示す。無負荷での測定である。CFRPに比較して回折強度が5分の1程度で弱い。CFRPの場合と同様に、111、220回折を一つのピークとして測定した。Fig. 7にはMD材のPPS相の負荷方向および垂直方向応力に対するsin²ψ線図を示す。直線性はかなり悪いが、回帰直線を求めその傾きから求めた負荷方向σ₁^mおよび垂直方向応力σ₂^mと負荷応力の関係をFig. 8に示す。負荷応力に対して、平行な方向の応力と負荷応力の比は0.339であり、CFRPの場合0.233よりは大きく、PPS相がより高い応力分配係数となる。一方、垂直方向の応力はあまり変化しなかった。一方、TD材についても応力の測定を行ったが、データのばらつきが大きく信頼できるデータは得られなかった。これは回折強度が弱いために、精度が悪くなったためと考えられる。

　また、炭酸カルシウム(CaCO₃)相についてもsin²ψ線図を求めたが、ばらつきが大きく、有用なデータは得られなかった。さらに、CaCO₃の弾性定数は不明であり、今後の検討が望まれる。これらの実験結果に共通しているのは，GFRP中のPPS相、CaCO₃相の割合が低く、十分の回折X線強度が得られなったことが原因と考えられる。さらに、6 mm程度の板厚の内部応力の測定のためには、エネルギをあげ、例えば20 keVを採用することが必要になるものと考えられる。

Table 2 Measurement conditions for GFRP.

Fig. 6 Diffraction profile of PPS from MD specimen of GFRP for different sin²ψ.

Fig. 7 2θ-sin²ψ diagram of TD specimen of GFRP.

参考文献：

[1] 田中啓介, 所 昇平, 小池祐基, 江上 登, 秋庭義明, 材料, 63(7), 514 (2014).

[2] K. Tanaka, T. Kitano, N. Egami, Engineering Fracture Mechanics, 123, 44 (2014).

ⒸJASRI

(Received: October 21, 2015; Early edition: July 11, 2017; Accepted: July 18, 2017; Published: August 17, 2017)