Volume5 No.1

背景と研究目的：

　近年の半導体高性能化および長期信頼性の観点から、半導体パッケージ用樹脂には高度な耐熱性、電気絶縁性、熱伝導性、耐湿性が求められている。半導体パッケージ基板は、熱硬化性樹脂と無機フィラーを主成分とする樹脂と金属(配線およびリードフレーム)で構成される複合部材である。それら異種材料間の弾性率と線膨張率(CTE)が異なるため、半導体パッケージ製造工程における熱プレスおよび熱硬化、半田リフローなどの複数の加熱冷却過程を経ることにより樹脂と金属界面に発生する熱応力が残留応力として蓄積し、半導体パッケージの歪みや反りの要因となる。それらは、金属界面の密着性に影響を与え、最終的には剥離という半導体パッケージにおける致命的な不良につながる。そこで半導体パッケージ製造の各工程において発生する熱応力をその場観察し、残留応力発生メカニズムを把握することができれば、プロセス改善による金属界面の密着性向上や信頼性評価時間の短縮につながることが期待される。我々はこれまでに0次元検出器であるシンチレーションカウンターを用いたsin²ψ法^[1–3]による半導体パッケージ用樹脂/銅界面の残留応力の評価手法を確立し、更に試料加熱ステージを併用することで熱プロセス中における応力変化のその場観察にも成功した^[4–7]。

　一方で、樹脂の熱硬化過程におけるリアルタイムな応力変化を検出するためには、測定時間を数分オーダーにまで短縮する必要があるため、1測定当たり約40分を要する測定時間が課題となった。そこで測定時間の短縮化を目的として課題番号2015B1622にて2次元検出器PILATUS 300Kを用いた応力解析を試みた^[8]。しかし、回折強度を十分に得るために長い露光時間を要したため測定時間の短縮化は達成できなかった。そこで本課題ではビームサイズの最適化により露光時間を短縮し、測定時間の短縮化を検討した。

実験：

　半導体パッケージにおける樹脂/銅界面のモデル試料として、銅箔(厚さ12 μm)上に半導体パッケージ用樹脂であるシリカフィラー含有熱硬化性樹脂を成形・後硬化し、直径40 mm、厚さ1.5 mmの円盤状の測定試料を得た。X線回折測定はBL19B2ビームラインのHUBER社製多軸回折計を用いて行い、入射X線エネルギーは8.00 keVとし、回折X線はPILATUS 300Kにより計測した。課題番号2015B1622ではスリット形状(入射X線ビームサイズ)を縦0.2 mm × 幅1 mmとしたが、本課題では短時間露光で回折ピーク形状を解析可能な回折強度を得るために、縦1 mm × 幅1 mmに変更した。測定に用いた結晶面はCu(331)面であり、8.00 keVにおける無歪銅の(331)面の回折角を138.4°とした^[9]。得られた2次元回折像はsin²ψ法の側傾法により解析を行った。sin²ψ法におけるオフセット角度ψは、0.0, 13.6, 24.1, 31.8, 38.6, 41.8, 45.0°とした。ここで、ψ角は試料を水平設置した際の試料面法線と回折面法線のなす角と定義する^[1]。残留応力計算に用いる銅の弾性率とポアソン比は、各々65.0 GPa、0.343とした^[10]。また、試料下流側において検出面法線と入射光軸が平行となる位置を検出器アーム角tth = 0°と定義し、PILATUS 300Kの各ピクセル位置(a, b)における2θをtth = 0°で観測されるダイレクトビーム座標(a₀, b₀)、(a₀, b₀)におけるカメラ距離(CL)、およびtthの関数として算出した。カメラ距離(CL)は、tth = 0°および5°で観測されるダイレクトビームの検出面上におけるピークトップ座標の移動量(dx)より、CL = dx/tan(5°)より算出した。なお、tthの走査面は入射光軸とψ = 0°における試料面法線を含む面である。さらに、アントンパール社製試料加熱ステージDHS1100を用いて、樹脂の熱硬化過程を想定し熱時の応力評価を実施した。

結果および考察：

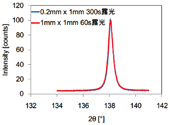
　検出面法線と入射光軸とのなす角が8.00 keVにおける無歪銅の(331)面の回折角と一致するよう、検出器アーム角tthを138.4°に設定した(図１)。ψ = 0.0°においてPILATUS 300Kにより得た測定試料のCu(331)面の2次元回折ピークを図２に示す。さらに、図２中に示す円周方向の角度をγと定義し^[11]、γ = 267.5–272.5°において回折強度をセクター平均し1次元化した結果を図２に合わせて示す。また、1次元化回折プロフィールのピーク強度および半価幅に関して、入射X線ビームサイズを縦0.2 mm × 幅1 mm、露光時間を300 sとした際と同等の結果が、入射X線ビームサイズを縦1 mm × 幅1 mm、露光時間を60 sとした際においても得られた。また、ψ = 45.0°においても同様の結果が得られた。これより露光時間を1/5に短縮した場合においてもビームサイズの拡大により解析可能な回折ピークが得られ、また測定精度も劣らないことが確認できたため、以下入射X線ビームサイズを縦1 mm × 幅1 mm、露光時間を60 sで測定を行った。これにより課題番号2015B1622では40分程度の測定時間を要していたのに対して本課題では10分以下にまで短縮化することに成功した。

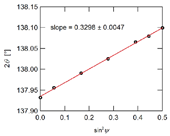
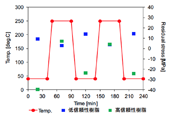
　次に、熱サイクル信頼性が異なる2種の半導体パッケージ用樹脂と銅箔界面残留応力の熱時のその場観察結果を行った。残留応力は、図２中に示す円周方向の角度γ =267.5–272.5°において回折強度をセクター平均し動径方向に1次元化することで回折ピークの1次元プロフィールを求め、文献記載の手法に従い^[11]ピアソンVII関数フィッティングによりCu(331)面の回折ピークトップ2θ*を算出し、複数のψにおける2θ*の変化からsin²ψ法により算出した。代表的な2θ–sin²ψ線図として、高信頼性樹脂の熱硬化処理前における室温の結果を図３に示す。半導体パッケージ用樹脂の熱硬化過程における応力変化を図４に示す。低信頼性樹脂は加熱測定中残留応力変化が小さく常に引張応力を示したのに対して、高信頼性樹脂は室温-加熱間の残留応力変化が大きく、圧縮応力と引張応力の間を変化した。当初、低信頼性樹脂は残留応力の絶対値や変化量が大きいことを予測した。しかし、得られた結果から、長期信頼性と相関するパラメータとして圧縮方向にはたらく残留応力が考えられた。これらより長期信頼性樹脂開発にむけて、圧縮方向または引張応力といった応力の方向を制御した樹脂設計が必要である可能性が示唆された。

図１　残留応力測定セットアップ

図２　各スリットサイズにおけるCu(331)面の回折ピーク(左)およびその1次元プロフィール(右)

図３　高信頼性樹脂の熱硬化処理前における室温での2θ–sin²ψ線図

図４　半導体パッケージ用樹脂モデル試料の熱時その場観察結果

今後の課題：

　本課題により確立した残留応力評価手法は、複数の回折環を同時に観測することが可能であるため、樹脂/銅界面と樹脂/銀界面等の複数の異なる界面における残留応力の同時測定への展開を予定している(課題番号2016A1535)。これにより、今回着目した樹脂/銅界面のみならず、銀ペーストやメッキ加工部等、半導体パッケージ内部における異種材料間の残留応力を同時評価することで、さらに多面的な長期信頼性樹脂開発へのアプローチに繋がると考えられる。

　また、2次元検出器を用いた応力解析手法である2D法^[11]を適用することによっても測定時間は短縮可能と推定される。

参考文献：

[1] 田中啓介 他, "放射光による応力とひずみの評価", 養賢堂, 東京 (2009).

[2] K. Nakamae et al., J. Appl. Polym. Sci., 40, 2231 (1990).

[3] T. Nishino et al., J. Appl .Polym. Sci., 45, 1239 (1992).

[4] 若林みどり 他, SPring-8/SACLA 利用研究成果集, 3(2), 589 (2015).

[5] 若林みどり 他, SPring-8/SACLA 利用研究成果集, 4(2), 275 (2016).

[6] 若林みどり 他, SPring-8/SACLA 利用研究成果集, 4(2), 294 (2016).

[7] 若林みどり 他, SPring-8利用課題実験報告書, 2015A1729.

[8] 若林みどり 他, SPring-8利用課題実験報告書, 2015B1622.

[9] PDF card number: 01-070-3039.

[10] 小出昭一郎, "物理学", 真喜屋実孜, 裳華房, 東京 (2003) p89.

[11] B. B. He, “Two-Dimensional X-Ray Diffraction,” John Wiley & Sons, Inc., New Jersey (2009).

ⒸJASRI

(Received: March 9, 2016; Early edition: November 25, 2016; Accepted: December 12, 2016; Published: January 31, 2017)