Volume4 No.2
SPring-8 Section B: Industrial Application Report
き裂先端特異応力場における局所応力測定系の開発
Development of Local Stress Measurement System in Stress Singularity Field at Crack Tip
a(株)豊田中央研究所, b横浜国立大学
aToyota Central R&D Labs., Inc., bYokohama National University
- Abstract
-
機械部品では応力集中部の局所的な応力が強度や寿命を支配する場合が多く、特に疲労き裂先端の特異応力場における局所応力の実測が重要である。本課題では放射光回折法により微小領域の応力を測定する実験系を構築した。鋼の表面においてき裂先端および遠方の応力を測定した結果、き裂先端部では約8倍の応力となり特異応力場の傾向が得られた。今後、応力分布の実測や照射領域が測定応力におよぼす影響の検討などを行う。
キーワード: 回折、応力ひずみ、微小領域、疲労き裂
背景と研究目的:
自動車からの環境負荷をいっそう低減するためには軽量化が有用である。軽量化と同時に高い信頼性や安全性を両立するには、部品に作用する負荷を把握し、損傷メカニズムを正確に理解する必要がある。自動車では、構造材料および機能材料として金属、セラミックスや樹脂など種々の材料が接合して使用される。異種材料を接合した部品では、製造工程で線膨張係数の差などによる残留応力が発生し、使用時には温度分布や形状不均一性などによる応力が発生する。これらの応力は分布を有しており、部品の信頼性や寿命は最弱部の応力に依存する。特に寿命は疲労き裂の伝ぱ過程で決定づけられるため、き裂先端の局所部における応力の実測が重要である。き裂先端の近傍は特異な応力場となり、一般的に負荷応力とは異なる大きさや成分を持つ。理想的な連続体においては、この特異応力場を線形破壊力学等で見積もることができる。一方、実部品の材料微視構造は不連続かつ不均質である場合が多く、複雑な変形履歴も応力状態に影響するため、応力を推定することは難しく、実部品における実測が求められている。
応力測定にはX線回折法が有用である。しかし、従来の実験室X線は輝度が小さくエネルギーも限られるため、微小部の応力測定には限界があった。高輝度な放射光を利用すれば、き裂先端などの局所部の応力測定が可能になると期待される[1-3]。微小領域の放射光回折測定では、照射領域が測定応力におよぼす影響など十分に解明されていない点があり、正確な応力測定にはこのような課題を解決するための実測装置が必要である。そこで本課題では、き裂先端の微小領域において放射光回折法で応力測定を実現する実験系の構築を行った。
実験:
測定試料は、深さ1 mmの片側切欠きを導入した短冊状の鉄鋼材料である(長さ70 mm × 幅10mm × 厚さ2 mm)。予め応力比R = 0.1の4点曲げ負荷で疲労き裂を導入した。き裂伝ぱと共に徐々に負荷を減少させながら最終き裂長さを2 mmとした。材料は、微小領域の放射光照射からも回折環が得られるよう粒径2 μm 程度の超細粒鉄鋼材料を使用した。計測はSPring-8のビームラインBL33XU(豊田ビームライン)で行い、微小領域応力測定のためのゴニオメータを立上げた。応力測定のセットアップを図1に示す。今回は試料の表面における局所応力の測定を目的とし、放射光のエネルギーは材料内部への侵入が無視し得る波長7.1 keVとした。放射光が空気で減衰しないように光路にはHeパスを設置した。放射光照射領域は回折角度によらず試料表面上で200 μm × 200 μmの一定となるよう入射側スリットを制御した。検出器には小型軽量なCd-Te半導体放射線検出器を用いた。
き裂先端近傍における応力を測定するには、試料を負荷しながらその場回折測定をする必要がある。そこで、4点曲げ装置を製作してゴニオメータに搭載できるセットアップとした。これをゴニオメータに搭載し、応力測定時には最大応力拡大係数Kmax = 10.4 MPa√mとなるように、き裂側が引張りになるよう曲げ負荷を行った。き裂材を一定変位で負荷する場合、荷重が大きいとクリープにより徐々に荷重が低下する場合がある。本セットアップで応力計測中に荷重が低下しない最大値としてKmax = 10.4 MPa√mとした。き裂伝ぱ方向に対して垂直な方向の応力σ11を測定した。応力測定の位置は、疲労き裂の先端、先端からの距離x = 0.1 mmの近傍点、および遠方で特異応力場から離れたx = 4 mmの点の3箇所とした。

図1 鋼表面におけるき裂先端近傍の応力測定セットアップ(BL33XU)
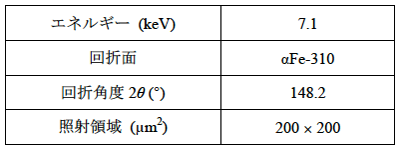
測定条件を表1に示す。回折計測にはαFe-310回折(回折角度2θ = 148.2°)を使用した。試料表面での計測のため、応力測定はsin2ψ法の並傾法で行った。ビームタイムの制約上、sin2ψの値は0、0.25および0.5の3点とした。試料表面上の照射領域がほぼ一定となるようθの変化とともに入射側スリット高さを逐次変化させた。回折弾性定数は単結晶の弾性定数をもとにKronerモデルで求めた。
表1 放射光回折応力測定の測定条件
結果および考察:
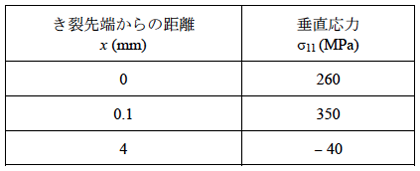
き裂先端からの距離x = 0.1 mmにおける回折プロファイルを図2に示す。また、回折角度2θとsin2ψの関係を図3に示す。これらから求めたき裂伝ぱ方向に垂直方向の応力の計測結果を表2に示す。疲労き裂先端のx = 0 mmにおける垂直応力σ11 = 260 MPa、およびその近傍のx = 0.1 mmにおける350 MPaは、遠方のx = 4 mmにおける垂直応力−40 MPaより著しく大きくなっており、き裂による応力集中(特異応力場中の局所応力)が計測できていると考えられる。遠方のx = 4 mmにおける垂直応力が負となるのは、4点曲げで負荷しているため、き裂とは反対側の端に近いこの点では圧縮が発生するためである。また、き裂先端においてx = 0.1 mmより垂直応力が減少するのは、測定領域にウェイク領域(応力を分担しないき裂開口部)が含まれるためである。これらの結果から、本測定系により局所応力の測定に目処が得られたと言える。
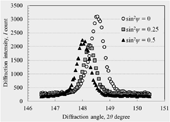
図2 き裂先端からの距離x = 0.1 mmにおける回折プロファイル
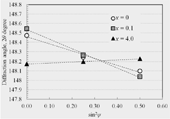
図3 回折角度2θとsin2ψの関係
表2 き裂伝ぱ方向に垂直方向の応力測定結果(4点曲げ)
今後の課題:
本課題ではビームタイムの制約により、応力の分布を密に得るまでには至らなかった。今後、き裂の延長上で距離が短いxの間隔で応力を実測することにより、特異応力場の実分布形状を得る。また、照射領域を変えることで、得られる測定応力はどのように変化するか検証する。
参考文献:
[1] 秋庭義明, 鈴木賢治, 日本機械学會論文集A編, 74 (739), 302 (2008).
[2] 鷲見裕史, 水谷安伸, 土肥宜悠, 秋庭義明, 田中啓介, 材料, 54 (4), 440 (2005).
[3] Y. Akiniwa, H. Kimura and T. Sasaki, Advances in X-Ray Analysis, 52, 493 (2009).
ⒸJASRI
(Received: December 16, 2015; Early edition: February 25, 2016; Accepted: June 24, 2016; Published: July 25, 2016)






