Volume4 No.1

Background and Purpose

　Multiferroics, where magnetic ordering and ferroelectric polarization coexist, can be categorized intoseveral classes based on the mechanism. One of well-known mechanisms is spin-driven ferroelectricity ^[1,2]. When cycloidal spin structure is realized, the anions located in the middle of the two magnetic ions shift tothe off-center position due to the spin current or inverse Dzyaloshinskii-Moriya mechanism. The prototypical multiferroic in this class is perovskite TbMn_O3. In this mechanism, the ferroelectricity emerges as a result of magnetic ordering, and thus coupling between the magnetism and ferroelectricity is inevitably strong. However, the magnitude of the electric polarization observed in this class of material is typically small as compared with proper ferroelectrics, such as perovskite BaTiO₃. Another well-known multiferroic is perovskite BiFeO₃^[3], where the 6s lone pair of Bi ion is responsible for ferroelectricity and localized magnetic moment of Fe ion is responsible for the magnetism. Electric polarization of BiFeO₃ is large, but the coupling between magnetism and ferroelectricity is small, because the magnetism and ferroelectricity are governed by different ions.

　Perovskite Sr_1-xBa_xMnO₃ is a multiferroic material which has different origin from the mechanisms mentioned above ^[4]. The pristine SrMnO₃ is paraelectric with large dielectric constant at low temperatures. Upon doping the larger Ba ion into the Sr site, the ferroelectric instability increases, resulting in an increaseof dielectric constant. Phonon mode softening is also observed with increasing x by optical reflectivity and inelastic x-ray scattering measurements. Increasing x ≥ 0.45 causes the system to become ferroelectric with off-center displacement of magnetic Mn⁴⁺ ions. The electric polarization of Sr_0.5Ba_0.5MnO₃ is 13.5 μC/cm² at 2 K, which is comparable with a proper ferroelectric material BaTiO₃. Sr_0.5Ba_0.5MnO₃ orders antiferromagnetically below T_N = 185 K. At that temperature, the magnitude of the lattice distortion which reflects the electric polarization changes by 70 %, which indicates the strong coupling between magnetism and ferroelectricity of the system, as expected from the fact that the Mn⁴⁺ governs both ferroelectricity and magnetism. In order to clarify the coupling between magnetism and phonon dynamics, we measured inelastic x-ray spectra of the ferroelectric perovskite manganite.

Experimental Summary

　A single crystal of Sr_0.5Ba_0.5Mn_0.97Ti_0.03O₃ was grown by a two-step procedure as described in Ref. [4]. The properties of magnetism and ferroelectricity of Sr_0.5Ba_0.5Mn_0.97Ti_0.03O₃ are qualitatively the same as those of Sr_0.5Ba_0.5MnO₃. We observed electric polarization value of 8.7 μC/cm² at 2 K and ferroelectric transition temperature is 400 K. Antiferromagnetic transition was observed to take place at 188 K. Inelasticx-ray scattering measurements were performed at BL35XU ^[5]. A silicon (11 11 11) backscattering monochrometer was used. The crystal was mounted with <001> pseudo-cubic axis horizontal and <110> axis vertical, so that we could access the reciprocal space Q = (005) + (qq0) ^[6]. In this setting, the scattered intensity from the phonon modes polarized parallel to the <001> axis can be detected.

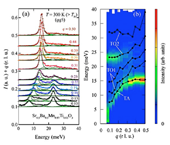
Fig. 1. (a) Inelastic x-ray scattering spectra for Sr_0.5Ba_0.5Mn_0.97Ti_0.03O₃ at 300 K at the wave vector of (qq5). The solid circles correspond to the measured data, where the peak due to the elastic scattering is subtracted by fitting the resolution function to the pseudo-Voigt function. The solid lines denote the fitting results based on the damped harmonic oscillator model [Eq. (1)], and the green lines are the individual damped harmonic oscillator peaks. (b) Color plot of the intensity in the energy- wave vector plane. The solid circles are the oscillator energies obtained by fitting the spectra to Eq. (1)

Results and Discussion

　Fig. 1 shows the inelastic x-ray scattering spectra at 300 K. Elastic scattering was removed by using the instrumental resolution function, and the intensity is divided by the Bose factor [n(ω)+1] . The spectrum at q = 0.10 has two distinct features at E = 7 and 23 meV. These peak structures are also observed in the paraelectric phase of Sr_1-xBa_xMnO₃ (x ≤0.3), where lower and higher energy peak are assigned to transverse acoustic (TA) and optical (TO2) modes, respectively ^[7].

In addition, a broad feature is observed in between. The feature corresponds to another optical (TO1) mode, which exhibits softening in the paraelectric phase. Three modes are discernible in this energy range for the paraelectric Sr_1-xBa_xMnO₃. Considering the lower lattice symmetry of the tetragonal ferroelectric material (as compared to the cubic paraelectric) we fit the obtained spectrum to five phonon modes modeled as damped harmonic oscillators, whose intensity is [8]:

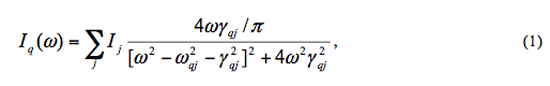
where q is the wave vector, ω is the energy transfer, ω_qj and γ_qj are the frequency and linewidth of the jth mode with intensity I_j. We were not able to fit all the parameters simultaneously, and therefore, we first varied I_j and ω_qj, and then changed γ_qj, separately. This fitting reproduces the observed spectra well as shown in Fig. 1(a). The lowest energy peak is assigned to the TA mode, next lower two modes are to TO1 modes, and other modes are to TO2 modes. With increasing q, the intensity of the (Bose normalized) peak originating of the TA mode increases and it disperses to higher energy. The TO2 peak is less pronounced and merges with the TO1 modes in the high q region. The mode energies, ω_qj, obtained by fitting are shown as a function of q in Fig. 1(b).

　The temperature dependence of the spectra at fixed q = 0.10 and 0.39 is shown in Figs. 2(a) and 2(b), respectively. Below T_N = 188 K where the tetragonal distortion decreases drastically ^[4], one of the TO1 modes becomes prominent, resulting in the shoulder structure of lowest energy peak at q = 0.10 and distinct peak at q = 0.39 (arrows inthe figures). We have performed the two-step fitting with the 5-mode damped harmonic oscillator model, and it reproduces the spectra well in the entire temperature range, as shown by the solid lines in the figures. The intensity, energy, and the linewidth of the TO1 modes obtained by this fitting based on Eq. (1) are shown as a function of temperature in Fig. 3. The intensity ofthe lower TO1 mode increases below T_N, as shown in Fig. 3(a), implying the coupling between the phonon and magnetic ordering in the system. This observation is in accord with general cases of magnetic ordering where a tiny structural distortion occurs simultaneously, and indeed a drastic change of lattice distortion was observed in this system ^[4]. As shown in Fig. 3(c), the linewidth of the TO1 mode at q = 0.39 decreases, as in the case of the paraelectric Sr_1-xBa_xMnO₃ with x = 0.3 ^[7]. However, in the case of x = 0.3 material, the reduction in the linewidth in the magnetically ordered state becomes more significant as q vector becomes smaller, and this is apparently not the case in the present result.

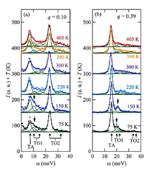
Fig. 2. Temperature dependence of the inelastic x-ray scattering spectra at (a) q = 0.10 and (b) q = 0.39.

　The change in the energy of the damped harmonic oscillator upon magnetic ordering is barely visible, as shown in Fig. 3(b). This is in contrast to the results of the paraelectric Sr_1-xBa_xMnO₃ materials, where hardening of the TO1 phonon mode is clearly observed upon magnetic ordering ^[7]. The hardening in the paraelectric materials can be described by a spin-phonon coupling model:

where ω_m (ω₀) is an energy of the phonon mode with (without) spins, α is a coupling constant, and ＜Si ∙ Sj＞ is a nearest-neighbor spin pair correlation function. Within this model, the magnitude of α in the present　ferroelectric Sr_1-xBa_xMn_0.97Ti_0.03O₃ is smaller than those of paraelectric materials with x ≤ 0.3. This suggests that the dynamical fluctuation of electric dipole is needed for larger α ^[9], and this type of spin-phonon coupling is rather reduced once long-range ferroelectric order is established. For more detailed discussion, quantitative comparison with the appropriate the oretical model is indispensable.

Fig. 3. Temperature dependence of (a) intensity, (b) energy, and (c) linewidth assigned to the two transverse optical (TO1) modes as obtained by fitting based on Eq. (1). The values at two different q (q = 0.10 and 0.39) are shown. The values of the TA and TO2 modes are not displayed.

Acknowledgements

The authors are grateful to H. Sakai for fruitful discussion. This work was partly supported by Funding Program for World-Leading Innovative R&D on Science and Technology on “Quantum Science on Strong Correlation” from the Japan Society for the Promotion of Science (JSPS).

References

[1] S. –W. Cheong and M. Mostovoy, Nat. Mater. 6, 13 (2007)

[2] Y. Tokura and S. Seki, Adv. Mater. 22, 1554 (2010)

[3] G. Catalan and J. F. Scott, Adv. Mater. 21, 2463 (2009)

[4] H. Sakai et al., Phys. Rev. Lett. 107, 137601 (2011)

[5] A. Q. R. Baron et al., J. Phys. Chem. Solids 61, 461 (2000)

[6] A. Q. R. Baron et al., J. Phys. Chem. 69, 3100 (2008)

[7] H. Sakai et al., Phys. Rev. B 86, 104407 (2012)

[8] B. Fåk and B. Dorner, Physica B 234-236, 1107 (1997)

[9] T. Katsufuji and H. Takagi, Phys. Rev. B 64, 054415 (2001)

ⒸJASRI

(Received: July 4, 2015; Early edition: September 25, 2015; Accepted: December 11, 2015; Published: January 25, 2016)