Volume1 No.2
Section B : Industrial Application Report
ゴムの振動伝達特性に及ぼすフィラー凝集サイズの影響
Effect of the Filler Aggregation Structure Size on Vibration Transmission Characteristic of Rubber
a東海ゴム工業株式会社, b名古屋工業大学 大学院工学研究科
aTokai Rubber Industries, LTD., bNagoya Institute of Technology
- Abstract
ゴム中の粘弾性特性に及ぼすフィラー分散状態の影響について調査した。フィラーの分散状態の変化は、ゴムとフィラーの混練時間を変更することで実施した。混練時間が長くなると静的弾性定数は変化せず動的弾性率が低下することで動倍率が低下した。この動倍率の低下は、混練時にゴムとフィラー間において化学的ないし物理的吸着が起こり、フィラー界面でのすべりによる粘性が原因の動的弾性率が低減されたことによると推察される。これを確認するためゴムに伸張を与え(ゴムに4.5%歪みをかけ)超小角散乱測定を実施した。その結果、混練時間を長くした試料からは散乱パターンに異方性が認められた。このことは、ゴムとフィラーであるカーボンブラック界面での化学的ないし物理的吸着ができ構造に異方性が発現したものと考察される。以上のことから混練時間を最適化し、フィラー界面での化学的、物理的吸着を強固にすることがゴムの低動倍率化に効果があることが確認された。今回実施した微小歪みを与え極小角散乱測定を行うことは、ゴムとフィラー間の結合の有無を判定する手法として利用できると考えられる。
キーワード: ゴム(rubber),補強材(reinforcing material),静的ばね定数(static spring constant),動的弾性率(dynamic modulus),界面(interface),異方性(anisotropy)ゴム,充てん剤,凝集構造
背景と研究目的:
ゴムの高性能化を図る上で、ゴム配合に用いる補強材(カーボンブラックなどのフィラー)は必要なものである。ゴム中の補強材の機能を発現させるためには、ゴムと補強材間の界面吸着を強固なものにする必要がある。界面吸着が強固になることで、ゴムに振動が加わった時に補強材界面でのゴムとの摩擦が低減され歪依存性の小さい防振ゴムができ、車両の快適性向上につながる。
前回までに小粒子径カーボンブラック(以下、CB)程、CBの凝集体が形成するネットワーク構造が増加し貯蔵剛性率の向上に関与していることが推定された[1]。
今回の実験は、サイズの異なるCBを用い混練時間を変更することでCBとゴムの混練時間を変更し、ゴムの物性への影響ならびに補強材の分散性について調査を行った。
実験:
ゴムとしてイソプレンゴムを使用した。ゴム中へのCBの混練は、密閉式混練機(容量2400 ml)を用いて行った。架橋剤の混練は8インチロールで実施した。加硫は、熱板温度160℃のプレスにてプレス圧15 MPaで20分間行った。得られた2 mm厚のゴムシートを物性測定ならびに超小角散乱(USAXS)および小角散乱(SAXS)測定に用いた。USAXS (カメラ長42.2 m,q 0.005〜0.2 nm-1)、SAXS (カメラ長2.7 m,q 0.1〜3 nm-1)はSPring-8のBL19B2で行った。ビームサイズは約200 μm。カメラ長の校正はコラーゲン試料の回折ピークを測定して行った。X線エネルギーは118 keVで露光時間5分とした。検出器はPILATUS 2Mを使用した。
ゴムの伸張状態での測定は、歪み印加方向が検出器(二次元パターン)の赤道方向に対して平行になる位置関係で測定した。これらの測定からゴム特性とCBの分散性について考察した。今回使用したCBの特性を表1に示す。表1のRgは粒子の慣性半径を表し、Rは粒子が球状であることを仮定した場合の半径であり、R=Rg(5/3)0.5の関係がある。RgおよびRは、各試料について行ったUSAX-SAXS測定から得られる試料中の平均構造を代表する値である。
表1. カーボンブラック(CB)特性とゴム中の分散状態
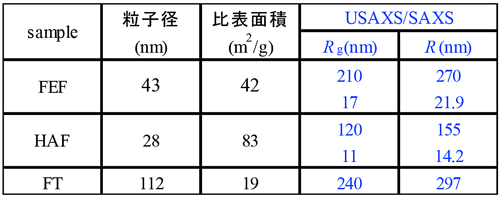
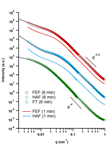
混練時間6分の試料(FEF、HAF、FT)の散乱プロファイル(図1)をUnified-Guinier Power Law[2]を用いてフィッティングを行った。散乱プロファイルの解析結果から、FEF試料において一次粒子半径21.9 nmが凝集して半径270 nm程度の二次粒子が存在し、HAFにおいては一次粒子半径14.2 nmが半径155 nm程度の二次粒子を形成していることがわかった。さらに、小角側の散乱強度もそれぞれ増大していることからCBがより高次の構造を形成していることが伺える。
図1. カーボンブラック充てんゴムの散乱プロファイル
黒の実線はUnified-Guinier Power Lawによる計算プロファイルを表す。
括弧内の数字は混練時間を表す。
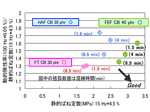
次に、ゴムへのCBの混練時間を変更した時の静的ばね定数と動倍率(動的弾性率の静的ばね定数に対する比)の関係について図2に示す。
図2. ゴムの混練時間が及ぼす動倍率への影響
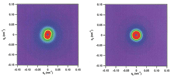
FEF、HAF試料(図2のFEF CB 40 phrおよびHAF CB 30 phr)において混練時間を長くするほど、動倍率が低下した。一方、FT試料においては動倍率に混練時間依存性はほとんどなかった。図1に示すように、これらのゴム試料を無伸張状態の小角散乱パターンには練り時間の違いによるフィラーの分散状態の差は認められなかった。次に、ゴムに4.5%という低伸張をかけた状態で測定を行うと図3に示すように超小角散乱の二次元パターンに異方性が確認された。一方、混練により動倍率に変化がほとんどなかった系(FT CB30 phr)では4.5%の歪み印加USAXSパターンの変化もほとんどなかった。
図3. ゴムに4.5%伸張歪を与えた時のUSAXSパターン
左図 HAF-CB 右図 FT-CB
結果および考察:
ゴムに使用する補強材の効果を発揮させるためには、ゴムと補強材間の吸着を強固なものにする必要がある。今回の実験では、ゴムの動倍率が低いものほど歪み印加時に超小角散乱の二次元パターンに異方性が確認された。異方性が現れたq領域はq < 0.04 nm-1の領域であり、CB(補強材)が凝集した二次粒子以上の大きさの構造に由来するものが延伸により変化したことになる。おそらくCB二次粒子がネットワーク状に繋がったものが歪みにより変形していることによると考えている。一方、散乱パターンに異方性が現れなかったFT試料においては粒子のネットワーク構造というよりSAXSからの粒子サイズが300 nm程度であり、カタログ値の112 nmと比較してそれほど大きくないことから一次粒子そのものを観察している可能性もあると考えている。そうであるとすると、延伸による異方性が測定範囲には現れなかったことに対応すると考えている。もう少し大きなスケールでネットワーク構造に異方性があるのかは不明である。現時点では今回の観測範囲において異方性が現れた系においてゴムの補強効果が見られる結果であった。
また一次元散乱プロファイルの解析から、FT試料では散乱強度がqの-4乗に比例しているのに対し、FEF、HAF試料のPorod領域の散乱強度のq依存性は、散乱強度がqの-4乗より大きなべき乗に比例しており、フラクタル表面を形成していることがわかる。このことは、FEF、HAFの方がCB とゴムの界面近傍が荒いことを示唆し、ゴムと補強材間の強固な吸着をしていることを示唆する結果であると考えられる。
以上のことから、低伸張をかけて散乱測定を行うことで、界面領域の解析と歪み印加状態での構造の異方性発現からゴムと補強材間の吸着状態を評価することが可能になったと思われる。今のところ伸長方向と異方性パターンの関連性については再現性(異方性が出現する再現性はある)がなかったので、そのことは課題として残っている。今後、ゴムと補強材間の吸着状態とゴムの動倍率の相関を評価する手法として有効利用できるように評価手法の検討を進めていきたいと考える。
今後の課題:
今回の実験で、ゴムの動倍率特性向上と伸張による構造の異方性発現に関係があることが確認された。この異方性発現はゴムと補強材間の強固な吸着が生じたことと関連性があると推察される。今後、なぜ異方性パターンに再現性がないのかを解明しゴムと補強材間の吸着状態の有効な評価方法として検討を行っていきたい。
参考文献:
[1] 2011A1745(重点産業利用課題成果報告書)
[2] G.Beaucage:J.Appl.Cryst.28,717 (1995).
©JASRI
(Received: May 7, 2012; Accepted: March 8, 2013; Published: June 28, 2013)