Volume3 No.1

背景と研究目的：

　小型電子部品のアクチュエータやセンサーは鉛を主成分としたPb(Zr,Ti)O₃（以下、PZT）圧電セラミックス材料が広く使用されている。しかし近年、鉛を含む物質の環境負荷の懸念からPZTの使用が段階的に制限されつつあり、鉛を含まない圧電セラミックス材料（以下、無鉛圧電材料）の研究が進められている。無鉛圧電材料の研究は1990年代から進められ、2003年頃から関連する論文数は急激に増加しておりPZT代替物の必要性が高まっている。ただし現状は鉛の圧電体がまだ主役であり多くの電子部品に使用されている。

　無鉛圧電材料は、RobertsによるBaTiO₃の圧電性発見^[1]からBaTiO₃を基にした材料が研究されていたが、キュリー温度が低く、実用温度範囲が狭いといったデメリットから、キュリー温度が高い(Na,K)NbO₃（以下、NKN）を基にした材料へ移っていった。NKNではNKNにLiをドープしてPZTに迫る圧電特性を持った組成系(以下、LNKN)がSaitoらにより報告^[2]されたが量産が難しく実用化には至っていない。この報告の他にもNKNの研究は進められ、WangらによりSrTiO₃^[3]、CaTiO₃とBaTiO₃^[4]、BaZrO₃^[5]といった添加物によるキュリー温度や圧電定数の対応を研究した論文がいくつか報告されたが、圧電特性はPZTに及ばず実用化には至っていない。

　更に、セラミックスの積層技術が進歩し圧電定数が小さいNKNでも積層することで実用化の可能性がKawadaらにより報告^[6]され始めた。我々は、NKNより単層で圧電特性の高いLNKNを用いることでさらなる圧電特性向上を研究している。LNKNの圧電特性は、添加元素の種類や量に依存するが、構造的な側面からメカニズムが十分に明らかにされていない。我々は結晶構造解析から材料デザインの指標について明確化することを目的とする。

　以上の研究背景を受け、本課題は材料として過去の研究^[2-5]から特性のさらなる向上が期待される(1-x){(Na,K)_1-xLi_y}NbO₃-xBaZrO₃を用いる。

　本課題の目標値は、LiNbO₃ならびにBaZrO₃の添加が圧電特性を向上させるメカニズムについて精密結晶構造から究明することである。さらに可能ならばLiが特性に寄与するメカニズムの推察を行う。

　本目標を達成すれば、積層において1層当たりの圧電特性が向上し、圧電体の積層数を増やし大きく特性向上した無鉛圧電デバイス設計の指標が期待できる。

実験：

1.実験試料作製

　実験試料(1-x){(Na,K)_1-yLi_y}NbO₃-xBaZrO₃セラミックスは固相法により作製した。表1に試料作製の組成水準を示す。

表1. 実験試料の組成水準

実験水準は電気特性に顕著な差が認められた組成に絞り込んで作製を行った(なお、測定は組成水準に明記した試料のみとする)。

　セラミックスの作製方法を以下に記す。原料として、K₂CO₃、Na₂CO₃、Nb₂O₅、Li₂CO₃、BaCO₃、ZrO₂を(1-x){(Na,K)_1-yLi_y}NbO₃-xBaZrO₃の組成比になるよう秤量した。そしてエタノールとジルコニアボールを混ぜボールミリングを24時間行った。温風で乾燥した後、ポリビニルアルコール(PVA)をバインダー剤として混合し厚さ100 μmのシート成型を行いφ10 mmの金型で打ち抜き円板成型体を作製した。

　円板の焼成はアルミナザヤを用いて大気雰囲気にて1000ºCで2時間行った。焼結円板にニッケル電極をコーティングし圧電特性評価用の試料とした。圧電特性の測定は、日本電子材料工業会標準規格EMAS6100に基づいて行った。

　焼成した円板をメノウ乳鉢で粉砕後、沈降法により整粒し測定用の粉末を得た。粉末はφ0.2 mmのボロ・シリケートガラスキャピラリーに充填し密封することで測定用の試料とした。

2.測定条件

　X線回折データの取得は次の測定条件で行った。測定はBL19B2に設置してある大型Debye-Sherrercameraを用いた。検出器は試料から286.48 mm離れた位置のImaging plateを用いた。使用したX線の波長は0.70709(3) ÅでNIST(米国国立標準技術研究所)の674b(CeO₂)を室温で測定した回折線位置から決定した。入射X線のビームサイズは縦0.3 mm、横3.0 mmを使用した。

　測定時間(積算時間)はRietveld解析を行うため、回折強度の統計精度が最も高くなる20分で行った(本件試料の場合)。測定中は粉末試料中の粗大粒による回折線を防ぐためガラスキャピラリーを自転させ、測定温度は室温にて行った。なお、相転移温度を評価するために200 Kから800 Kまで100 Kの温度間隔で温度変化測定を行った。温度変化は2°C/minで行い温度のオーバーシュートを防止するため目的の温度の1°C以内では0.2°C/minで温度変化をコンピュータープログラムにより制御した。

　表1に示したセラミックスにはNi粉末を混合した試料(擬似内部電極)も測定予定であったが、Rietveld 解析用の測定が再測定で長引いたため本課題では測定を行わなかった。この試料の測定目的はNiが圧電材料に微少量固溶しているか否かを定量的に研究することであったが、別途課題申請して行う予定である。

3.分析・解析方法

　焼成した円板焼結体の組成は、ICP-AESを用いて分析を行い所望のモル比になっていることを確認した。そして結晶構造解析はRietveld解析法^注)を用い、ソフトウェアにRIETAN-FP^[7]を使用した。

^注)Rietveld解析法とはX線回折パターンに対し結晶構造モデルを仮定し理論計算を行って実測値に最も近くなるX線回折パターンを再現するものである。実測値と計算値の一致は非線形最小二乗法の成り立つ範囲で実行され誤差が最小の解を求める。この解とは格子定数と結晶構造パラメータ(原子座標、占有率、熱振動、構造因子)であり物性と関連するパラメータを精密化することが可能である。

結果および考察：

　図1 に(1-x){(Na,K)_1-yLi_y}NbO₃-xBaZrO₃のX線回折パターンを示す。図1(a)はLi添加量を変化させた場合の回折パターン、図1(b)はBaZrO₃添加量を変化させた場合の回折パターンである。さらに特徴的なパターン変化の範囲を図1中の右上に示す。ICDD(国際回折データベース)の標準回折パターンデータと実測パターンを比較すると、図1の回折パターンは図1(a)のy=0.08の組成を除き全て斜方晶系に同定できた。

図1. (1-x){(Na,K)_1-yLi_y}NbO₃-xBaZrO₃のX線回折パターン(室温)。(a)x=0.035、y=0.00から0.08の回折パターン変化。(b)y=0.06、x=0.035から0.075の回折パターン変化。

続いて温度変化測定の結果から求めた結晶系の変化を図2に示す。

図2. (1-x){(Na,K)_1-yLi_y}NbO₃-xBaZrO₃の温度変化X線回折パターンより求めた200 Kから800 Kまでの相図。(a)Liの添加量に対する結晶系の変化。y=0.08は擬正方晶であった。(b)BaZrO₃の添加量に対する結晶系の変化x=0.065以上ではキュリー点が低温側へシフトし、300 K付近では正方晶系との混晶系のような斜方晶系が出現した。

図2(a)に示すようにLi添加に対してキュリー点のシフトは認められなかった。x=0.08では斜方晶から正方晶への転移温度(第二相転移点)がやや低温側にシフトする効果が認められた。また図2(b)に示すようにBaZrO₃の添加によりキュリー点は100 Kほど低温側へシフト認められ、Liに比べより相転移温度のシフターとして効果的であることが確認できた。従来ラボ用XRDでは、昇温中にLiやKの蒸発現象により組成比がずれ、正確な相図を把握できなかった。

　次に電気特性との対応についてLi濃度との対応を前ページの図1に示す。そして、図3にLi添加量を変化させた場合の圧電特性d₃₃とkpを示す。いずれもy=0.06(where x=0.035)で最大になっており圧電材料として優れた組成域であることが分かる。

　そこで、Li添加量の増加とともに結晶構造がどのような変化をしているのか調べるためRietveld解析を行った。図4には圧電特性が最大になったy=0.06(where x=0.035)におけるRietveld解析結果を示す。

　Rietveld解析の結果y=0、0.02、0.04では斜方晶であったが、y=0.06の場合は斜方晶と正方晶ならびに立方晶の混晶系であることが明らかになった。図4の解析結果は(a)斜方晶のみでRietveld解析をした場合と(b)混晶系(斜方晶+正方晶+立方晶)でRietveld解析した場合を比較したものである。

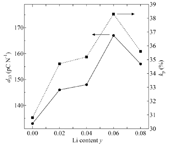
図3. Li添加量(y)と圧電特性(d₃₃ならびにkp)の変化。y=0.06(where x=0.035)の時に圧電特性が最大値になる。

図4. (1-x){(Na,K)_1-yLi_y}NbO₃-xBaZrO₃(x=0.035、y=0.06)のRietveld 解析結果。(a)斜方晶単相モデル、(b)混晶モデル(斜方晶+正方晶+立方晶)のRietveld解析結果。

　Rietveld解析結果の収束程度を比較するため、各結晶モデルの信頼性因子R(標準不確かさ)を表2に示す。

表2. 計算モデルによるRietveld解析結果比較(信頼性因子Rの比較)

　R_wpは回折パターン全体に対する値、R_Bは各回折線の積分強度(面積)に対する値、R_Fは結晶構造因子に対する値である。

　斜方晶+正方晶+立方晶モデルの時は、斜方晶単相モデルに比べ信頼性因子Rが改善され顕著に減少しているため混晶系が正しい構造解であることが分かる。Rietveld解析から求めた各結晶相の重量比は、斜方晶(64wt%)、正方晶(27wt%)、立方晶(9.0wt%)であり分極方向の多い斜方晶が占める割合が多かった。

　Rietveld解析の結果より求めた格子定数値をLi添加量に対してd₃₃と共に描画したグラフを図5に示す。y=0.00、0.02、0.04は斜方晶である。y=0.04ではa軸長が僅かに長く格子体積の増加を示すが原因は明らかでない。なおLiの固溶サイトの解析であるが、y=0.06で混晶系に転移したためy=0.00からy=0.04までをRietveld解析で比較した。

　具体的にはLiの固溶サイトが異なる2つのモデル(1)酸素12配位のAサイト固溶、モデル(2)酸素6配位のBサイト固溶を用いて解析を行った。Liの原子散乱因子が比較的高いsinθ/λ≤0.2 Å^-1の実測回折線強度比に変化が認められたがモデル(1)と(2)ではどちらもRietveld解析の結果に有意な差は認められなかった(従って本解析でLiの占有格子サイトはBaの増加によりイオン半径が大きくなるAサイトに固定して解析を行った)。

　次にy=0.06では混晶系となりd₃₃が最大になる理由としては、(1-x){(Na,K)_1-yLi_y}NbO₃-xBaZrO₃(x=0.035、y=0.06)が、PZTで見られるようなMPB^[8]を持つためと考えられる。PZTにおけるMPBの圧電特性はBerlincourtらが報告している^[9]。本材料のMPBは図5中の点線で示したように、PZTのような組成領域のほとんど無いMPBではなく、一定の組成領域を持ったものと推察している。

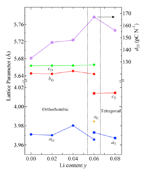
図5. Rietveld解析から得られた各結晶相の格子定数変化とd₃₃との対応。各軸の変数に付けた添え字は各結晶相の頭文字である。

　MPBで圧電特性が最大になる理由は、斜方晶の分極方向<001>と<110>に加えて正方晶の<001>と<100>が加わるため、誘電的弾性的に柔らかい状態が発現した効果によるものと推察している。

　混晶中に存在する立方晶(9.0wt%)はセラミックスを焼成した際の結晶格子の歪により発生し、先に述べた斜方晶と正方晶の境界に存在して2つの結晶の格子不整合を緩和しているものと推察している(最近Magomeら^[10]により格子傾斜相と呼ばれる緩和相の増減が圧電特性と対応すると報告されている)。

　y=0.08では混晶系から単相系の正方晶に相転移する。正方晶のc/aは1.012でy=0.06に比べ増加するがd₃₃は減少している。この理由は、結晶格子の歪が緩和され安定した正方晶になった為である。

　次に3ページ目の図1(b)に示したBaZrO₃量の変化と結晶構造解析の結果を述べる。Li添加の場合と同じように各組成の回折パターンでRietveld解析を行った。解析結果は代表例としてd₃₃が最大値を取るx=0.075を用いて図6に示した。

図6. (1-x){(Na,K)_1-yLi_y}NbO₃-xBaZrO₃(x=0.075、y=0.06)のRietveld解析結果。(a)斜方晶単相モデル、(b)混晶モデル(斜方晶+正方晶+立方晶)のRietveld解析結果。

　図6(a)は斜方晶単相で精密化した結果で実測パターンと合致していないが、混晶系モデル(斜方晶+正方晶+立方晶)で精密化すると実測パターンと良く合致する。計算結果の収束程度を比較するため信頼性因子Rを表3に示した。

表3. 計算モデルによるRietveld解析結果比較(信頼性因子Rの比較)

　斜方晶+正方晶+立方晶モデルでは信頼性因子Rが単相モデルより顕著に小さくなる。ゆえに3相の混晶系が正しい構造解と判断した。この混晶系はMPBと推察している。それは前後に明瞭な相転移がある訳ではないが、圧電特性を考慮するとMPBと考えるのが自然だからである。

　BaZrO₃の変化量と圧電定数の変化を図7に示す。d₃₃は、x=0.055、0.065、0.075の時に増加する傾向が認められる。一方、k_pはx=0.035から0.075へ増加するに伴い4%程度減少する傾向が認められた。さらにx=0.085ではx=0.075に比べ5%の顕著な減少となった(x=0.085は圧電定数のみ測定しており今回の課題では測定していない)。

図7. (1-x){(Na,K)_1-yLi_y}NbO₃-xBaZrO₃(where y=0.06)のBaZrO₃量の変化と圧電特性の変化。

　結晶系はRietveld解析結果が示すようにBaZrO₃量を増加していくといずれも斜方晶と正方晶そして立方晶の混晶系であった。x=0.035のRietveld解析の結果は図3と同じであるので参照頂きたい。図7の圧電特性のうちk_pはBaZrO₃の増加に伴い減少するため機械変位量も減少している。これは斜方晶と正方晶の結晶格子の歪が減少し格子軸長の比率は段々と1に近づいていくことが予想される(例えば正方晶ならc/a~1)。

　そこで上述した予想を検証するため、Rietveld解析から精密化した格子定数を用いて格子軸比を求め、d₃₃とプロットしたグラフを図8に示す。d₃₃の値は図7と同じものである。

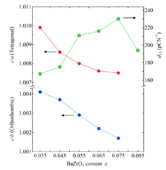
図8. Rietveld解析から求めたBaZrO₃量に対する斜方晶と正方晶の格子軸比の変化とd₃₃の変化。

　予想したように斜方晶と正方晶の格子軸比は減少し1に近づいていることが分かる。つまりk_pが減少した理由は結晶格子の歪が減少したため機械的変位量も減少したものと考えられる。

　そして、図8に示すようにd₃₃が格子軸比の減少に伴い増加している理由について考察する。x=0.035、0.045では分極方向に印加された電場に対して分極方向の歪はとても小さく約d₃₃=160~180(pCN^-1)である。

　一方、x=0.055、0.065、0.075では格子軸比の小さい結晶格子が電場方向に分極回転(ドメイン壁移動)を加えるため全体的にd₃₃が増加すると推察される。例としてBaTiO₃の場合であるがグレインサイズが1 μm以上の場合、格子軸比が減少するとd₃₃が増加することがHoshinaにより報告されている^[11]。

　以上まとめると、(1-x){(Na,K)_1-yLi_y}NbO₃-xBaZrO₃(x=0.035~0.075、y=0.00~0.06)のX線回折パターンからRietveld解析により精密な結晶構造解析を行った結果、圧電定数d₃₃が最大となる理由は、(1)x=0.035、y=0.06と(2)x=0.075、y=0.06の2ヵ所の組成で、混晶系(斜方晶+正方晶+立方晶)のMPBとなっているためである。またxの値が増加するのに伴い斜方晶と正方晶の格子軸比は減少していた。この理由は、低結晶性が電場印加に対するドメイン回転を増加させた可能性がある。

今後の課題：

　今回の実験で(1-x){(Na,K)_1-yLi_y}NbO₃-xBaZrO₃の結晶構造変化と圧電特性との概要は明確になった。しかしながら、さらに圧電特性に関与しているものはAサイトとBサイトへのLiとBサイトのZrの固溶状態による新たな分極の発現ではないかと考えている。そしてLi、Zr添加効果による結晶構造変化を詳細に解明し今回推察した分極回転(ドメイン壁移動)との整合も究明して行こうと考えている。これらの解析に当たっては、XANESやEXAFSを用いて調査を行っていく予定である。

参考文献：

[1] S. Roberts, Phys. Rev. 71, 890, (1947).

[2] Y. Saito et al., Nature, 432, 84-87, (2004).

[3] R. Wnag et al., Phys. Stat. Sol. (a), 202, R57-R59, (2005).

[4] R. Wang et al., Phys. Stat. Sol. RRL, 3, 142-144, (2009).

[5] R. Wang et al., Appl. Phys. Lett. 95, 092905-1-092905-3, (2009).

[6] S. Kawada et al., Appl. Phys. Exp. 2, 111401-1-111401-3, (2009).

[7] F. Izumi and K. Momma, Solid State Phenom. 130, 15-20(2007).

[8] E. Sawaguchi, J. Phys. Soc. Jpn. 8, 615, (1953).

[9] D. Berlincourt et al., Proc. IRE, 48, 220, (1960).

[10] E. Magome et al., Jpn. J. Appl. Phys. 54, 09LE05, (2012).

[11] T. Hoshina, J. Cerm. Soc. Jpn. 121[2], 156-161, (2013).

ⒸJASRI

(Received: August 25, 2014; Early edition: October 31, 2014; Accepted: January 16, 2015; Published: February 10, 2015)