Volume1 No.3

背景と研究目的：

　私達はNb系圧電材料(Na，K)NbO₃に工業的に入手し易く安価なCaTiO₃を用いて実用性のある(キュリー点が高く圧電d定数が安定している)材料を開発するため、CaTiO₃固溶濃度に対するキュリー点と圧電d定数の制御を試みている。しかしながら、CaTiO₃の固溶濃度に対してd定数変化が大きく安定した制御が十分にできておらず原因も明確になっていない。

　そこで私達は、結晶構造解析から制御因子を解明するため、SPring-8を利用し高精度な結晶構造解析を課題番号2011B1785:「X線回折による圧電体(1-x)(Na_0.45K_0.55)NbO₃ + xCaTiO₃の結晶構造解析」にて行った。課題番号2011B1785ではRietveld解析^[1]によりx = 0 〜 0.09における室温の結晶構造の精密化を行った。その結果、CaTiO₃固溶量がx = 0.03以上では、斜方晶と正方晶の混晶であり、モルフォトロピック相境界(MPB)が存在することを実験的に初めて明らかにした（従来は斜方晶⇒正方晶の相転移と認識されていた）。今までCaTiO₃の固溶による正確な構造変化についてはほとんど議論されていなかったが、MPB組成域に調整することにより圧電特性を最大にできる可能性が分かった。

　今回、私達は前回の結果と関連して、常誘電相の結晶構造解析を行う。CaTiO₃の固溶量が原子の結合力や熱振動異方性にどのように影響しているのか調べることを目的とする。同時に本材料の圧電機構を材料設計に働きかけ、安全な製品を作り出す指標を確立することも目的である。

実験：

　実験試料は、KNbO₃粉末（純度：99.8 %）とNaNbO₃粉末（純度：99 %）、そしてCaTiO₃粉末（純度：99.9 %）を所定のモル比で混合し1400°Cで2時間焼成して(1-x)(Na_0.45K_0.55)NbO₃+xCaTiO₃（x = 0, 0.03, 0.06, 0.09）単板セラミックスを作製した（NaとKの比率は物性値に対する経験値）。そしてこの単板を粉砕し平均粒子径3 μmの粉末を測定用とした。実験試料名と組成比を表1に示す。

表1．粉末X線回折測定用の試料名と組成比

　粉末化した試料は内径ϕ0.2 mmのリンデマンガラスキャピラリーの先端約1 cmに充填し、充填口を接着剤で密封した。粉末X線回折の測定はSPring-8のBL19B2に設置してある大型デバイ・シェラーカメラを使用した。

　検出器は十分に回折角2θが高角度の回折線まで捉えられるイメージング・プレート(IP)を用いた。照射したX線のサイズは縦0.3 mm × 横3.0 mmで、X線の波長は0.65912(6) Å{NISTのSi粉末を標準試料として較正した。( )内は最小二乗法の標準偏差}の単一波長光を用いた。試料の入ったガラスキャピラリーは測定中に自転させ、回折線に与える粉末粒子の選択配向や粗大粒子の影響が最小限になるようにした。X線の照射によるIPへの積算時間はIPのサチレーション・タイムを考慮して15分で行った。

　測定温度は800 Kで行った。昇温は高温窒素ガスをガラスキャピラリーに吹き付けて、20 K/minの速度で調整した。

　測定終了後、イメージング・プレートに記録した回折線の強度と位置を読み取り、回折線位置と回折線強度の二次元回折パターンデータを得た（2θ / 強度データ）。

結果および考察：

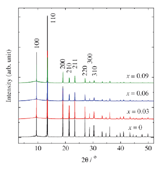
　測定の結果得られたNKN，NKNCT3，NKNCT6，NKNCT9の粉末X線回折パターンを図1に、算出した格子定数の変化を図2に示す。

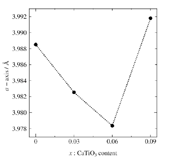
図1．800 Kにおける回折パターン(全て立方晶)　　図2．800 Kにおける格子定数変化

　定性分析の結果、800 Kでは全て立方晶(常誘電相)であることを確認した。図2には各CaTiO₃固溶量に対する格子定数変化を示した。立方晶なのでa軸をプロットしている。a軸長はx = 0.06で最小値を取ることが分かり、この濃度領域に構造的な特徴があることを示唆している。

　続いてRietveld解析を行った結果を図3に示す(FIETAN-FP Package^[2]を使用)。

図3．800 Kにおける立方晶のRietveld解析結果

CaTiO₃ content: (A) x = 0 (B) x = 0.03 (C) x = 0.06 (D) x = 0.09

　Rietveld解析の初期構造モデルはぺロブスカイト立方晶モデルで、空間群(S.G.)はP m-3m(No.221)である。図3中のR_wpなどはRietveld解析が正確に行えているのかを示す信頼性因子で、値が小さいほど良い。各信頼性因子は5%未満であり、非線形最小二乗法が十分に収束し実測値と計算値がよく合致していると判断した。

　Rietveld解析結果から求めた構造因子Fを元にして、最大エントロピー法(MEM)から立方晶の電子密度分布を求めた。電子密度分布の結果を図4に示す(描画にはVESTA^[3]を使用)。

図4．800 Kにおける立方晶の電子密度分布

等電子密度面: 0.6 e/ų。等高線描画範囲: from 0.45 to 0.95 e/ų

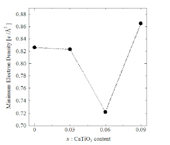
図5．Nb/Ti – O間の最小電子密度変化

　図4の下段は(200)でNb – O間およびNb/Ti – O間の共有結合性を比較している。x = 0.06ではNb/Ti – O間の電子密度が低くなっている。図2で示したようにx = 0.06では格子軸長(または格子体積)が最小であることから、系のポテンシャルエネルギーが最も安定している領域ではないかと考えられる。図5には電子密度分布から計算したNb – OおよびNb/Ti – O間の最小電子密度を示す。わずかなCaTiO₃の固溶量で最小電子密度が大きく変化していることが分かる。

　また前回の実験(課題番号2011B1785)から、室温ではx = 0.06近傍にMPB組成域が存在していることが分かっており、今回の電子密度分布の挙動と何らかの関係があると思われる。

　図4の上段は(200)と直交する(010)の電子密度分布を示している。図4下段の酸素と比較することで原子変位(熱振動)の異方性を可視化した。x = 0ではNb – O方向にややラグビーボール状の広がりを持つ。

　x = 0.03，0.06，0.09ではx = 0の様な異方性はほとんど認められない。

　本件では、MPB組成域を有するNb系圧電材料の常誘電相の構造解析を行った。その結果、CaTiO₃が6 mol%固溶した構造(800 K)においてエネルギー的に安定であることを間接的に示した。

今後の課題：

　今回の結晶構造解析からMPB組成域近傍の結晶構造(常誘電相)は、エネルギー的に安定していると考えられた。しかし、なぜMPB組成領域と対応しているのかが明確にできなかったため、Rietveld解析にDisorder model(Split-Atom model)^[4,5]を取り入れて熱振動の異方性をより正確に解析していく。

参考文献：

[1]H.M. Rietveld, J. Appl. Crystallogr., 2, 65 (1969).

[2]F. Izumi and K. Momma, Solid State Phenom., 130, 15-20 (2007).

[3]K. Momma, F. Izumi, J. Appl. Crystallogr., 44, 1272-1276 (2011).

[4]K. Fukuda, M. Ito and T. Iwata, J. Solid State Chem., 180, 2305-2309 (2007).

[5]名古屋工業大学大学院物質工学専攻，結晶性萌芽材料研究室ホームページ

　X線粉末回折パターンからの不規則性構造の解析

　(http://crystals.web.nitech.ac.jp/gaiyo.fukisokukozo.html), Accessed on July17, 2012.

ⒸJASRI

(Received: September 6, 2012; Early edition: August 30, 2013; Accepted: November 1, 2013; Published: December 10, 2013)