Volume8 No.2

背景と研究目的：

　「重い電子系」とは、ウランや希土類元素含む化合物において、高温で局在的に振る舞っていた f 電子が低温で伝導電子との混成を通じて遍歴性を獲得し、このとき、電子の有効質量が自由電子に比べ数百倍～千倍も重くなる物質群であり、強相関物理学において活発な研究分野を形成している。5 f 電子系の重い電子化合物である URu₂Si₂ では、5 f 電子の遍歴・局在性の変化、隠れた秩序、反強磁性秩序、超伝導など多様な物性を示すことが知られており、その本質は 5 f 電子が担っていると考えられる。磁化率や電気抵抗測定によれば、60 K 前後の温度で局在状態から遍歴状態に変化するものと考えられている[1]。更に低温の 17.5 K には「隠れた秩序」転移と呼ばれ、25 年以上にわたって未解明の問題がある[1-3]。これは、転移温度で比熱や磁化率等に明らかな異常が観測されているにも関わらず、未だ秩序パラメータが何なのか明らかになっていない現象である。

　また、URu₂Si₂ に圧力を印加した場合、あるいは、Ru の一部を Rh で置換した試料においては、低温で反強磁性相が観測される[4,5]。この反強磁性相は隠れた秩序相と競合しているものと考えられているが、シェブニコフ－ド・ハース効果の測定よると、隠れた秩序相と反強磁性相のフェルミ面には大きな違いは無いと報告されている[6,7]。

　5 f 電子の波動関数は、遍歴性の強い 3d 電子と局在性の強い 4 f 電子の中間的な広がりを持っているので、本来的に遍歴・局在の２重性を有すると考えられ、URu₂Si₂ の物性を理解するためには、電子状態に対する 5 f 電子の寄与を微視的な観点から明らかにすることが必要と考えられる。我々は、このような背景のもと、高分解能コンプトン散乱測定を用いて URu₂Si₂ の電子構造を、二次元電子占有数密度の観点から調べてきた。これまでに、隠れた秩序転移や 5 f 電子の遍歴・局在性クロスオーバーに伴う電子構造の変化を報告している[8,9]。本研究では、Ru の一部をRhで置換した U(Ru_0.97Rh_0.03)₂Si₂ の単結晶試料を対象に、その反強磁性相における電子構造を明らかにするため、高分解能コンプトン散乱の二次元再構成実験を行った。

実験：

　URu₂Si₂ 試料は、上述のように、低温で圧力を加えれば反強磁性に転移を起こすが、高圧力下でのコンプトン散乱測定は困難であったため、チョクラルスキー法により Ru の一部を Rh で置換した単結晶試料：U(Ru_0.97Rh_0.03)₂Si₂ を作成した[10]。その転移温度は、～12 K と見積もられる。また、核燃物質であるため、軸方向を決定したうえで、アルミ製の密封容器に封入した状態で放射光実験を行った。実際のコンプトン散乱二次元再構成実験には、BL08W に設置された高分解能コンプトンスペクトロメータを使用した。図１に実験配置図を示す。この測定における入射X線のエネルギーは、U からの蛍光X線を避けるため、U-K 吸収端より少し低エネルギーの 114.56 keV に設定した。試料によりコンプトン散乱されたX線は、Ge(620) 結晶アナライザーによりエネルギー分解され、位置敏感型2次元検出器によって測定される。運動量密度分布の二次元再構成解析を行うには、コンプトン・プロファイルの角度依存性の測定を行う必要があるが、試料は密封容器ごと回転させ、単結晶の（001）面内において、[100]軸と[110]軸の間で5方位の高分解能コンプトン・プロファイルを、それぞれ、温度 20 K と 11 K で得た。測定時間は、1方位につき ～1.5 シフトを要した。密封容器の径（内径：48 mm）は試料の大きさに比べて十分に大きく作製してあるので、密封容器と試料の結晶アナライザーに対する散乱角は異なる。そのため、容器からの散乱が試料によるコンプトン散乱に重なることはない。このようにして得られた各方向の測定データに対して、バックグラウンド、試料吸収、多重散乱、散乱断面積等の補正を行うことにより、コンプトン・プロファイルを求めた。ただし、コンプトン・プロファイルは、運動量密度分布を二重積分した量であり、全電子のプロファイルの重ね合わせになっているので、その形状から温度変化を見積もるのは難しい。そこで、各温度において得られた5方位のプロファイルを用いて、直接フーリエ変換法により、観測面に射影された2次元運動量密度分布を導出した。更に、この運動量密度分布に対して Lock-Crisp-West（LCW）法を適用して、2次元電子占有数密度（2 dimensional electron occupation number density:2D-EOND）を求めた[11]。これは、広い運動量密　LCW法により得られる2D-EONDが示す構造は、フェルミ面を横切る伝導バンドによって形作られている。即ち、伝導電子のみが その構造に寄与しており、内殻電子や完全な占有バンドの電子の寄与はない。フェルミ面と2D-EONDの関係を簡単な模式図に示してみよう。図2では、電子・フェルミ面をオレンジ色で、ホール・フェルミ面を青色で示している。2D-EONDの場合には、これらのフェルミ面で囲まれた体積部分が射影されて構造を形成するが、電子・フェルミ面は凸構造として、ホール・フェルミ面は凹構造として観測される。度分布をブリルアン・ゾーンの大きさで区分し、それらを１つのブリルアン・ゾーンに全て重ね合わせることによって得られる。

　　　　　　図１　実験配置　(a) 高分解能コンプトン散乱スペクトロメータの配置図、
　　　　　　　　　(b) 配置図と対応した実験時の写真、(c) アルミ製密封容器の写真

結果および考察：

　LCW 法により得られる 2D-EOND が示す構造は、フェルミ面を横切る伝導バンドによって形作られている。即ち、伝導電子のみが その構造に寄与しており、内殻電子や完全な占有バンドの電子の寄与はない。フェルミ面と 2D-EOND の関係を簡単な模式図に示してみよう。図２では、電子・フェルミ面をオレンジ色で、ホール・フェルミ面を青色で示している。2D-EOND の場合には、これらのフェルミ面で囲まれた体積部分が射影されて構造を形成するが、電子・フェルミ面は凸構造として、ホール・フェルミ面は凹構造として観測される。

　　　　　　　　　　　　図２：フェルミ面と2次元電子　占有数密度との関係

　図３に、実験・解析により得られた (a) 11 K と (b) 20 K の 2D-EOND を示す。この図は、元々の 2D-EOND から、5方位のプロファイルを平均したデータを用いて、同様な解析手順により求めた平均の 2D-EOND を差し引いたものである。 従って、電子数とホール数が等しい補償金属を仮定したことに相当している。例えば、ホール効果の測定結果等により、電子（ホール）数を推定できる場合には、それに合わせて、電子数密度のゼロレベルを調整することは可能である。

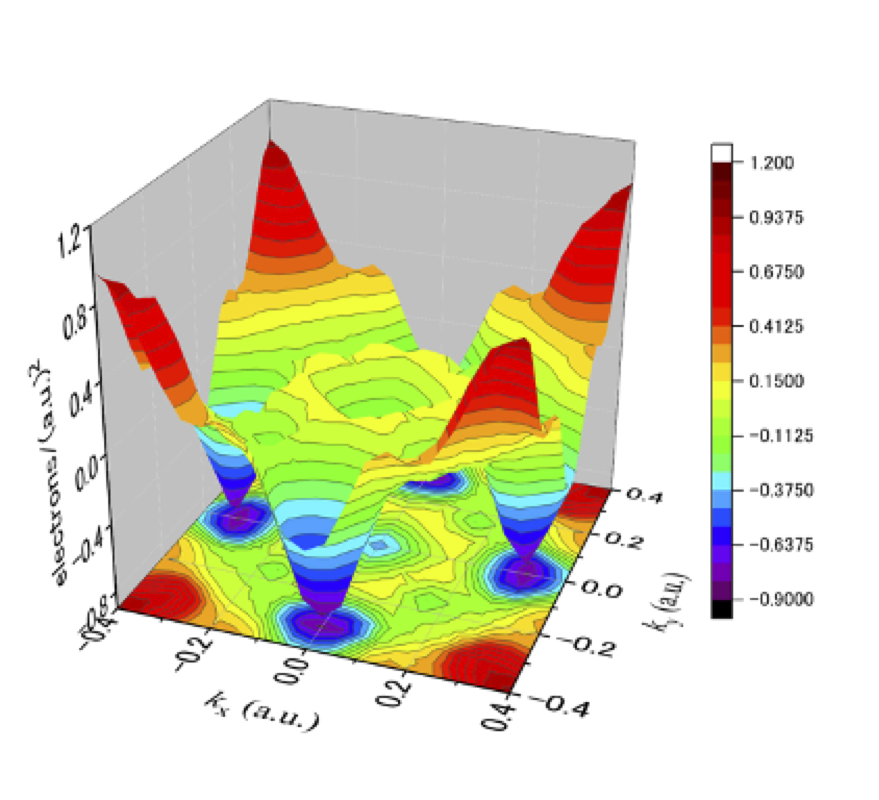
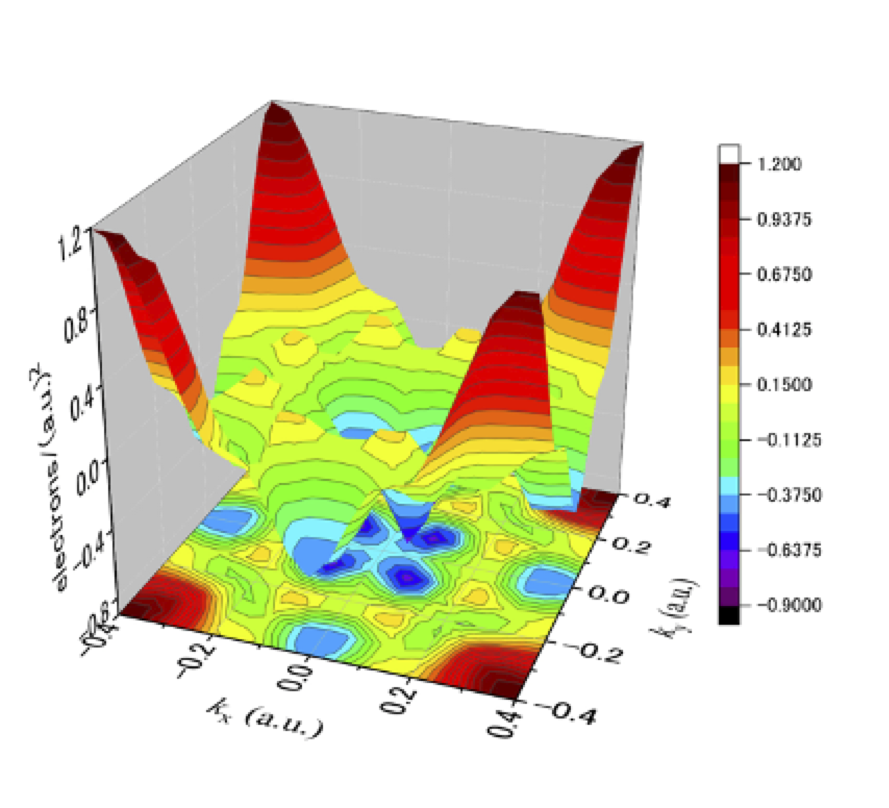
図３：　U(Ru_0.97Rh_0.03)₂Si₂ の2次元電子占有数密度 ： 元の 2D-EOND から、平均の 2D-EOND を差し引いているので、電子数とホール数が等しい補償金属を仮定したスケールになっている。

　常磁性状態と反強磁性状態ではブリルアン・ゾーンが異なるが、この試料の場合には、射影した観測面は同じになるので、常磁性状態の対称点を用いて、二次元面において、主な対称点がどこに射影されているか説明しておく。図３に示した 2D-EONDの原点では、Γ 点と Z 点の密度が重なっている。また、2D-EOND の四隅に相当する位置では、X 点と P 点の密度が重なって観測されている。図３を見ると、11 K、20 K ともに、原点付近の密度が低く、2D-EOND の四隅における密度が高くなっていることが分かる。この構造的な特徴から、どちらの温度においても、ブリルアン・ゾーンの Γ 点 －Z 点に沿った方向にはホール面が、X 点 －P 点に沿った方向には電子面が存在していることが推測される。温度：11 K を反強磁性相、温度：20 K を常磁性相と考えているが、両者の間の変化は、それほど大きなものではなく、全体的な構造は似ているように見える。ここで、既に報告されている URu₂Si₂ における 隠れた秩序転移に伴う 2D-EOND の変化と比べてみたい。この場合には、温度：17.5 K において常磁性相から隠れた秩序相に転移を起こすが、転移に伴い、2D-EOND の四隅に相当する位置での密度が大きく増加する。（参考文献：[8] Fig. 2 を参照）これは、常磁性相において 5 f 電子の一部は遍歴的であるが未だ局在的な成分が残っており、隠れた秩序相において、より遍歴的な状態へと変化したことを意味していると考えられる。隠れた秩序相への転移に比べて、反強磁性相への転移に伴う 2D-EOND の変化の割合はかなり小さく、5 f 電子の遍歴・局在性の大きな変化は無いことを示唆している。また、隠れた秩序相と反強磁性相の 2D-EOND を比べると、構造的特徴は似ており、シェブニコフ－ド・ハース測定の結果と矛盾はない[7]。ただし、今回の測定温度は 11 K であり、反強磁性秩序が充分に発達していない可能性がある。その場合、ほぼ常磁性の状態を観測していることになるので、そのために 20 K での 2D-EOND と大きな違いがなかったという可能性も考えられる。

今後の課題：

　上記のように、今回の実験では、測定温度が反強磁性への転移温度と近いため、本当に反強磁性状態の電子構造を観測できているのか疑問が残るところである。これは、試料用冷凍器の能力の問題でもあるが、現在では、最低到達温度：～2 K の冷凍器が使用できるようになっており、これを用いれば、充分に反強磁性秩序が発達した状態での測定が可能になるであろう。また、一般に、強相関系試料の多くは、より低温において磁性転移や超伝導など興味深い現象を示すので、新しい冷凍器の利用価値は高いと考えられる。更に、磁場や圧力などの測定環境と組み合わせることができれば、量子臨界現象に関わる電子構造の研究への発展が期待される。

参考文献：

[1] M. B. Maple et al., Phys. Rev. Lett. 56, 185 (1986).

[2] T. T. M. Palstra et al., Phys. Rev. Lett. 55, 2727 (1985).

[3] W. Schlabitz et al., Z. Phys. B 62, 171 (1986).

[4] M. Yokoyama et al., J. Phy. Soc. Jpn. 73, 545 (2004).

[5] S.-H. Baek et al., Phys. Rev. B 81, 132404 (2010).

[6] M. Nakashima et al., Physica B: Condensed Matter 329, 566 (2003).

[7] E. Hassinger et al., Phys. Rev. Lett. 105, 216409 (2010).

[8] A. Koizumi et al., Phys. Rev. B 92/, 125112 (2015).

[9] A. Koizumi et al., J. Phy. Soc. Jpn. 87, 064703 (2018).

[10] Y. Haga, H. Sakai, and S. Kambe, J. Phy. Soc. Jpn. 76, 051012 (2007).

[11] D. G. Lock, V. H. C. Crisp, and R. N. West, J. Phys. F 3, 561 (1973).

(Received: March 30, 2020; Early edition: June 26, 2020; Accepted: July 6, 2020; Published: August 21, 2020)