Volume8 No.2

背景と研究目的：

X線磁気円二色性 (X-ray magnetic circular dichroism: XMCD) 分光法は、元素や軌道状態を選択した磁気モーメントや電子状態の情報が得られるため、磁性研究の有力な手法となっている。XMCD の主要な応用のひとつとして、薄膜や積層膜磁性体試料に対する、層ごとの磁性や界面での誘起磁化の測定が行われている。たとえば、強磁性金属と貴金属から成る積層膜の　XMCD 研究は、垂直磁気異方性を有する磁気記録媒体の開発に有用な情報を提供する[1]。最近では、Pt など貴金属元素の大きなスピン軌道相互作用を利用した、スピントロニクス材料の研究が活発に行われている。磁性膜に電圧を印加することによる磁気異方性の制御や、スピン流の制御などが行われており、電子状態からのメカニズム解明が期待されている[2–5]。

このような薄膜試料に対しては、シリコンドリフト検出器 (SDD) 等を用いた蛍光法による XMCD 測定が主に用いられている。しかし、この方法では検出器の最大光子計数率によって統計精度が実質的に制限されており、測定精度としては 10^–3 オーダーの XMCD 信号の検出が実用的な限界であった。一方で、透過配置が利用できるバルク試料に対しては、ロックインアンプを用いた偏光変調法によって、10^–4 以下の XMCD 信号の検出が可能となっている [6]。しかし、スピントロニクス材料のような厚さ数 nm 以下の薄膜試料に対する透過配置での測定は、試料の吸収強度が小さすぎ、また基板によるX線減衰が大きすぎて現実的ではない。そこで、本研究では全反射配置での XMCD 法を開発し、薄膜試料に対するロックイン XMCD 測定を可能とすることで測定精度を向上させることを目的とした。全反射配置での EXAFS 測定は1980年代から試みられており、薄膜試料の表面での局所構造解析に用いられている [7–10]。硬Ｘ線領域での全反射配置での XMCD スペクトル測定は筆者の知る限りこれまでに報告がない。

実験：

試料として、厚さ 0.5 mm のガラス基板上にマグネトロンスパッタ法で成膜した Pt(1 nm)/Co(20 nm) の二層膜を用いた。本試料では過去に蛍光法での XMCD 測定が行われており、Pt L₃ 吸収端において信号強度約 10% の XMCD スペクトルが報告されている [1]。

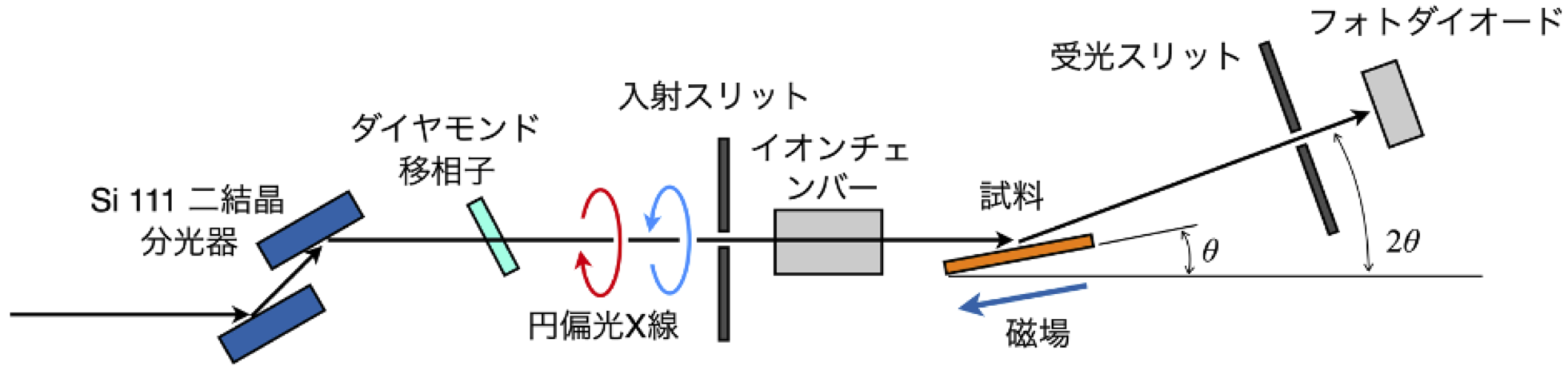
実験は BL39XU の実験ハッチ１で行った。測定配置を図１に示す。アンジュレーターからの放射光を Si 111 二結晶分光器により単色化し、厚さ 0.73 mm のダイヤモンド移相子により円偏光X線を生成し、40 Hz で左右円偏光のスイッチングを行った。入射スリットを用いてX線ビームの幅を 0.05 mm に制限し、斜入射条件で試料にX線を入射した。後述する全反射条件での試料上のＸ線ビームのフットプリントの大きさは 16 mm であった。入射X線強度をイオンチェンバーで、反射X線強度を Si PIN フォトダイオードで検出した。検出器以降の回路系は BL39XU で通常使用されている偏光変調法のセットアップ [6] を用いた。電磁石を用いて、入射X線に平行に（試料面内に）最大 1.1 T の磁場を印加した。

図１ 全反射XMCD測定の実験配置。

結果および考察：

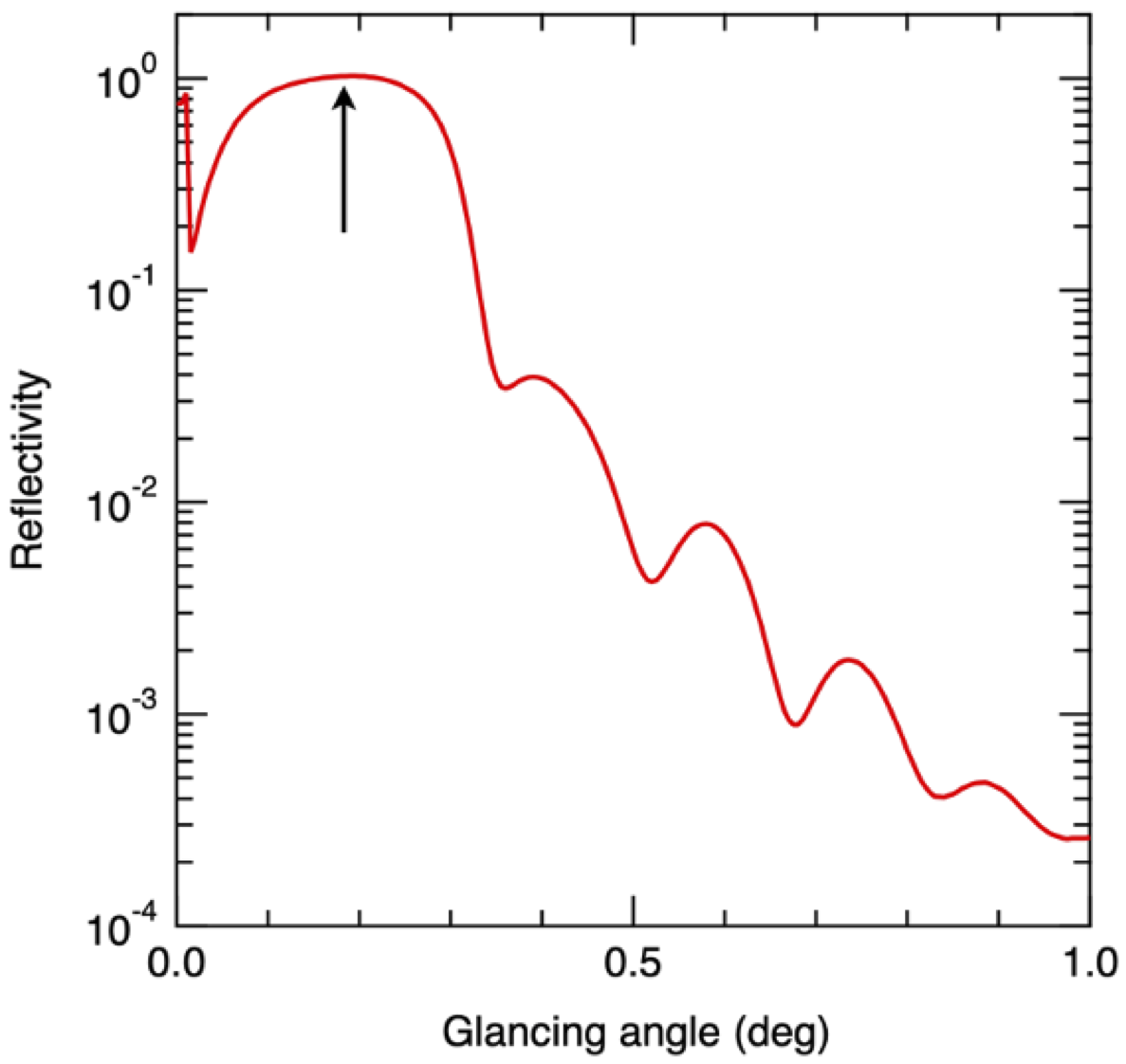
θ-2θ スキャンによって得られた Pt(1 nm)/Co(20 nm) 二層膜試料の反射率プロファイルを図２に示す。X線のエネルギーは 11.6 keV とした。全反射臨界角は 5.2 mrad であり、反射率プロファイルにみられる振動構造は、膜構造を Pt(1 nm)/Co(15 nm)/SiO₂、界面粗さ 1 nm と仮定したモデル試料のシミュレーション結果 [11] と定性的に一致した。

図２ Pt(1 nm)/Co(20 nm) 二層膜試料の反射率プロファイル。矢印で示す試料角度で反射 XMCD 測定を行った。

反射率が最大となる θ= 0.185º に試料角度を固定し、X線エネルギーを走査することで反射率スペクトルおよび反射率の XMCD スペクトルを測定した。図３(a)に、Pt L₃ 吸収端での反射率スペクトルを示す。赤線は試料に印加した磁場方向がX線と反平行、青は平行な場合の結果である。反射率スペクトルはX線吸収 (XAS) のクラマースクローニッヒ変換に相当し [7–10]、Pt L₃ 吸収端の前後で 5% の反射率変化が得られた。スペクトルの形状は通常の XAS スペクトルを反転した形状とよく一致した [7, 9, 10]。11.57 keV には、XAS スペクトルのホワイトラインに対応する構造が観察された。11.6 keV には XAS には見られないピーク構造が観測された。XMCD スペクトルにも対応する構造が観測されたが、正負の磁場に対して XMCD 信号の符号は変化せず、磁性とは無関係だと考えられる。ダイヤモンド移相子の同時反射によるアーティファクトの可能性が考えられるため、移相子結晶のアジマス角を変えた測定を行ったが、ピーク構造は依然として現れつづけた。また、ピーク構造は生データの入射強度 (I₀) スペクトルにはなく、反射強度 (I) スペクトルにだけ見られた。したがって試料に由来する信号だといえる。ビームタイム中には行えなかったが、入射角を変化させた測定によってこのピークの起源が明らかになるかもしれない。

図３ (a) Pt(1 nm)/Co(20 nm) 二層膜試料の Pt L₃ 吸収端での反射率スペクトル。(b) 反射率の XMCD スペクトル。磁場 +1.1 T (赤)で測定したスペクトル Δµ⁺、磁場 –1.1 T (青)でのスペクトル Δµ^–、および磁気信号だけを抽出した Half diff. スペクトル Δµ = (Δµ⁺–Δµ^–)/2 を示す。(c) 反射率 XMCD 信号により測定した Pt の元素選択的磁化曲線。

図３(b)に、試料からの反射Ｘ線の XMCD スペクトルを示す。偏光変調法によりロックインアンプを用いて測定した。測定時間は１エネルギー点あたり 12 秒、スペクトル１本あたり 20 分であった。Pt L₃ 共鳴に対して、通常の XMCD に対応するピーク構造が得られた。磁場方向の反転によって XMCD の符号が反転しており、磁性由来の信号であることが示された。黒丸は、正負の磁場に対して測定した XMCD スペクトルの差の半分を計算することで得られたスペクトルであり、11.6 keV 付近の構造のバックグラウンドが除去できている。反射 XMCD のピーク強度は、反射 XAS スペクトルのエッジジャンプの 23% であった。これは、蛍光モードで得られる XMCD 信号よりも大きな変化である。ただし、XAS に相当する反射率スペクトル自体のエッジジャンプは全反射強度の 5% と小さい。

図３(c)には、反射 XMCD 信号を用いて測定した元素選択的磁化曲線を示す。Ｘ線のエネルギーを XMCD 信号が最大となる 11.569 keV に固定し、磁場を変化させながら XMCD 信号をプロットした。通常の XMCD 測定と同様に元素選択な磁化曲線を取得することができた。

従来の SDD 検出器による蛍光法での測定と今回の反射率 XMCD 測定とで、得られた統計精度は同程度であった。偏光変調法を用いたにも関わらず、同程度の統計精度しか得られなかった理由は、全反射法では試料表面でのX線のフットプリントが大きくなるため、通常用いられる数 mm 角の試料では入射ビームサイズを 0.1 mm 以下に絞る必要があり、X線強度をロスするからである。試料の長手方向の大きさが 40 mm 程度以上の試料に対しては全反射配置が有効であると考えられる。なお、軟Ｘ線領域では直線偏光を用いた反射率測定（横磁気カー効果）によって高い効率で磁気信号を得る手法が報告されている[12]。今後の課題として、XMCD スペクトルを解析することで磁気モーメントの値を導出する sum rule については、全反射法で得られたスペクトルに対して適用可能かどうかの検証が必要である。たとえば、反射率スペクトルをクラマースクローニッヒ変換して吸収スペクトルを得た上で sum rule 解析を行う方法が考えられる。

参考文献：

[1] M. Suzuki et al., Phys. Rev. B 72, 054430 (2005).

[2] S. Miwa et al., Nat. Commun. 8, 15848 (2017).

[3] K. T. Yamada et al., Phys. Rev. Lett. 120, 157203 (2018).

[4] T. Kikkawa et al., Phys. Rev. B 95, 214416 (2017).

[5] T. Kikkawa et al., J. Appl. Phys. 126, 143903 (2019).

[6] M. Suzuki et al, Jpn. J. Appl. Phys. 37, L1488 (1998).

[7] G. Martens and P. Rabe, J. Physics C: Solid State Physics 13, L913 (1980).

[8] P. Borthen and H. H. Strehblow, Phys. Rev. B 52, 3017 (1995).

[9] D. Lützenkirchen-Hecht and R. Frahm, J. Synchrotron Rad. 8, 478 (2001).

[10] H. Abe et al., Jpn. J. Appl. Phys. 55, 062401 (2016).

[11] http://henke.lbl.gov/optical_constants/bilayer.html

[12] F. U. Hillebrecht et al., Phys. Rev. Lett. 75, 2224 (1995).

(Received: March 31, 2020; Early edition: May 27, 2020; Accepted: July 6, 2020; Published: August 21, 2020)