Volume8 No.2

Background and Purpose

  The possibility to observe nonlinear effects involving the interaction between x-rays and visible radiation was first considered almost fifty years ago [2, 3]. Those studies addressed several nonlinear processes including parametric down conversion (PDC) of x-rays into the optical region, sum-frequency generation (SFG) and difference-frequency generation (DFG). In the process of PDC of x-rays into visible light, a pump at x-ray wavelengths interacts with the vacuum field to generate two beams, one at x-ray wavelengths and the other at optical wavelengths. In the processes of SFG and DFG an intense optical beam interacts with an x-ray beam to generate a frequency-shifted x-ray beam. The authors of those papers highlighted the possibility of using the nonlinear interaction between x-rays and optical radiation as a probe to study the microscopic structure of chemical bonds and the density of valence electrons including the response to optical radiation with the atomic-scale resolution. However, until very recently there were no experimental evidence for nonlinear mixing between x-rays and optical radiation due to absence of sufficiently bright x-ray sources. In a recent work in LCLS, an x-ray beam at 8 keV (1.5498 Å) interacted with an intense optical beam at 1.5 eV (800 nm) to generate an x-ray beam at 8.0015 keV (1.5495 Å) [4]. The efficiency of the SFG process reported in that experiment was limited by the optical damage threshold and was estimated to be 3×10-7. Another pertinent effect is PDC of x-rays into the extreme ultraviolet (UV) regime [5]. In this type of nonlinear effects, the ultraviolet light is absorbed and only the hard x-ray wave is detected. Tamasaku and colleagues have shown experimentally that the response of the material to the UV radiation can be extracted from the measurement of the x-ray photons. The x-ray photons of the effect of PDC into visible radiation has also been observed recently with hard x-rays [6]. In this experiment the x-ray wave that corresponds to visible photons in the range of 280-650 nm was measured.

Like other wave mixing effects, x-ray DFG requires momentum conservation and energy conservation. The energy conservation is satisfied when the frequency of the generated photon is equal to the difference of the frequencies of the two input photons. Momentum conservation, which is usually denoted as phase matching, is satisfied when 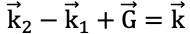 with  and denoting the k vectors of the x-ray pulses and and denoting the k-vectors of the visible radiation and the reciprocal lattice vector, respectively. The phase matching diagram is shown in Fig. 1. θ₁, θ₂, and θ_g are the angles of the prorogation directions of the pumping beams and the reciprocal lattice vector, respectively, with regard to the normal to the crystal surface. The solid lines represent the atomic planes of the crystal.

　　　　　　　　　　　　　　　　　Fig. 1: Phase-matching diagram.

Here we made the first attempt to explore DFG in a new regime where the measured radiation is in the optical regime and not in the x-ray regime. This is more than a straightforward extension of the pervious SFG experiment since the angles of both of the pumps are very close to the Bragg condition and because of the strong visible fluorescence.

Experimental Summary

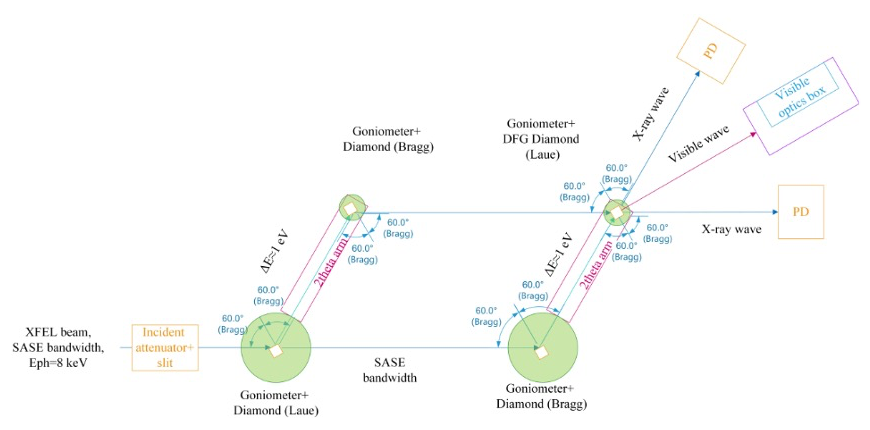
  The experimental setup is shown in Fig. 2. The nonlinear medium was a diamond crystal, where we used the reciprocal lattice vector perpendicular to the (220) atomic planes for phase matching. We used diamond as the nonlinear crystal due to it large x-ray damage threshold (>10¹⁵ W/cm²) and high band-gap.

　　　　　　　　　　　　　　　　　　　Fig. 2: Experimental setup.

We used quasi-monochromatic two-color x-ray pulses at 8 keV and at 7.998 keV in order to generate visible radiation centered at 600 nm, noting that the important aspect of the x-ray pulses is the frequency difference between them and not their actual central frequencies. We performed the experiment with the full SASE beam at the input and with the maximum available repetition rate and longest pulse duration. The beam was focused in the horizontal direction to a spot size of 4.5 µm while the vertical direction was not focused to allow very narrow rocking curves. We used the SACLA split and delay system for the experiment in order to obtain equal optical paths between the two x-ray pulses and both pump pulses hit the nonlinear crystal simultaneously. We used a diamond crystal at the Bragg angle for the (220) reflection at 8 keV to reflect this beam, while the other beam propagated in its original direction since the angle of the crystal is far from the Bragg angle of 8 keV. Next, the 7.998 keV beam was reflected from another diamond crystal tuned again for the Bragg angle of the (220) reflection. The other beam (at 8 keV) was Bragg reflected from another diamond crystal where we choose the (220) reflection to minimize the angular dispersion. Our experiment was the first use of the split and delay system with diamond crystals. We tuned the offsets of the two x-ray pulses from Bragg according to the phase matching angles of the DFG process. The DFG crystal was offset at -44.8 mdeg with respect to the Bragg angle to achieve the phase-matching conditions.

We used a multi-mode optical fiber with a collimating lens to collect the generated optical beam. We used an avalanche photodiode for the detection of the visible radiation. A visible band-pass filter with a bandwidth of 14 nm centered at 600 nm was inserted before the collecting lens to reduce the fluorescence. We used opaque curtains to reduce the background for the visible detector. We used coincidence electronics and the electrical sync signal of the XFEL to filter out the visible fluorescence.

We used glass to filter out the visible fluorescence generated by the x-ray pulse direct beam.

Results and Discussion

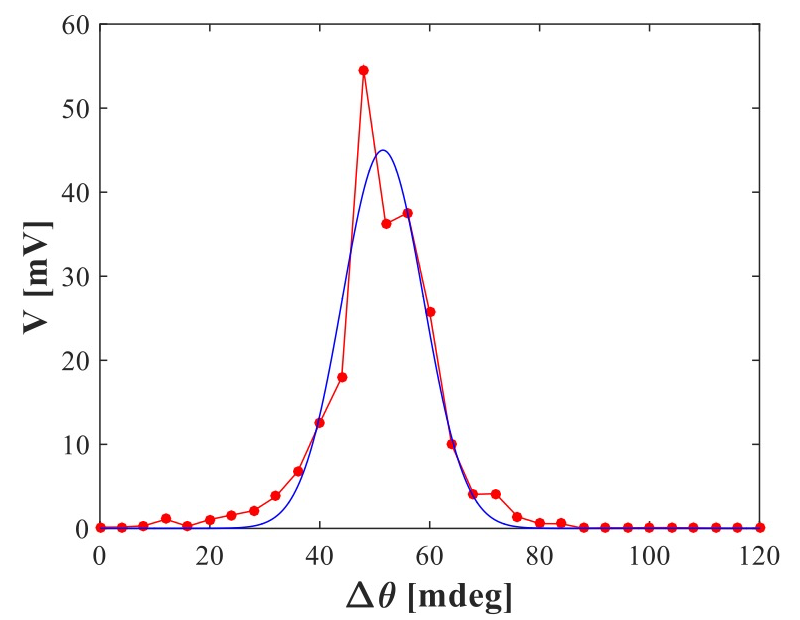
  We measured rocking curves of the diamond crystals in the geometries we described above. A typical rocking curve of the first diamond crystal (shined with the SASE beam) is shown in Fig. 3. The rocking curve width is about 17.4 mdeg (~304 μrad). We conclude from the narrow rocking curve that the crystal quality is suitable for the measurement of the DFG effect.

Fig. 3: Rocking curve. The blue line is the measured rocking curve and the red line is the Gaussian fit we used to calculate the width of the rocking curve. The solid line is a guide to the eye.

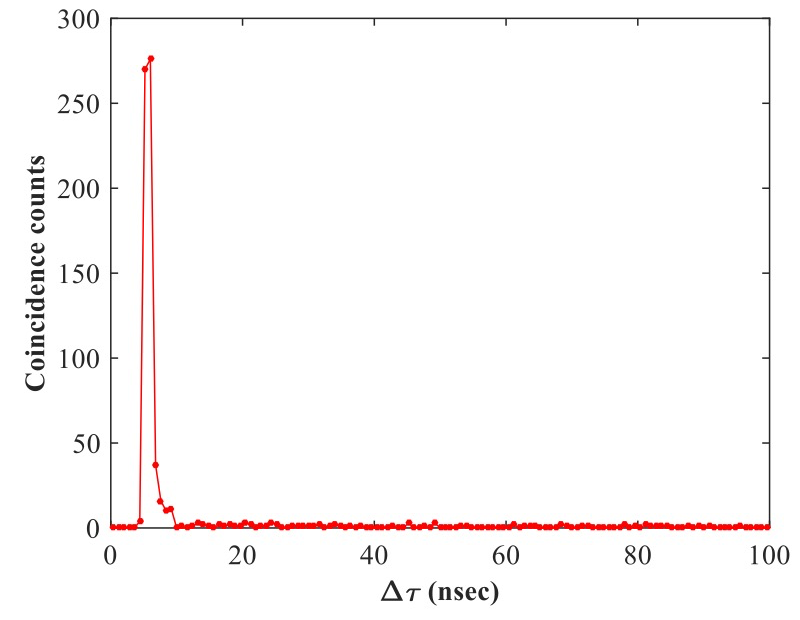
Next, we measured the time characteristics of the visible fluorescence from the nonlinear crystal by using coincidence electronics and the electrical sync signal of the XFEL to filter out the visible fluorescence. A typical time delay histogram of the visible fluorescence is shown in Fig. 4. Since the majority of the counts in the histogram occur within a 4.8 nsec delay interval from the sync pulse we conclude that the time resolution of the system, which is limited mainly by the time resolution of the sync signal, is insufficient to distinguish between the nonlinear effect and the fluorescence background.

Fig. 4: Time delay histogram. The solid line is a guide for the eye. The results were recorded without a visible filter. The average input pulse energy is about 500 µJ. The number of shots is 1800.

Finally, we tuned the crystals to the phase-matching conditions and attempted to measure the rocking curve of the effect but were unable to observe the nonlinear signal.

In summary, we did not observe optical difference frequency photons originated from a nonlinear process.

Challenges

  One big challenge is the inability to monitor the spatial overlap in the nonlinear crystal of the two input pulses simultaneously with the alignment of input angles. This is because for the setup we used we the spatial overlap was measured with a visible camera, which measured the fluorescence, while the angles were measured by a diode. We switched between the camera and the diode and could not measure the angles and the spatial overlap simultaneously. It is most likely that when we change the angles, we also affect the spatial overlap between the pulses.

The setup can be improved by moving the visible camera measuring the beam overlap in the non-linear crystal to the side or the top of the crystal.

The coincidence scheme can be improved by using a fast x-ray detector with a fast NIM output and a time resolution on the order of a nanosecond instead of the sync signal.

References

[1] E. Shwartz and S. Shwartz, Opt. Exp. 23, 7471 (2015).

[2] I. Freund and B. F. Levine, Phys. Rev. Lett. 25, 1241 (1970).

[3] P. M. Eisenberger and S. L. McCall, Phys. Rev. A 3, 1145 (1971).

[4] T. E. Glover et al., Nature 488, 603, (2012).

[5] K. Tamasaku et al., Nat. Phys. 7, 705 (2011).

[6] A. Schori et al., Phys. Rev. Lett. 119, 253902 (2017).

(Received: March 24, 2020; Accepted: July 6, 2020; Published: August 21, 2020)